利用条件生成对抗网络建立曲流河地质模型

胡勇，高小洋，何文祥，李顺利，朱建斌，司锦，陆雨诗

1.油气地球化学与环境湖北省重点实验室（长江大学，资源与环境学院），武汉 430100

2.中国地质大学（北京）能源学院，北京 100089

3.长庆油田分公司第一采油厂，陕西延安 716000

0 引言

储层地质模型是油藏描述的核心，也是连接油藏地质与石油工程的桥梁，准确表征砂体形态及分布，建立相应的储层地质模型具有重要的理论和现实意义[1-8]。曲流河砂体是重要的陆相碎屑岩储层类型，目前用于曲流河的建模方法主要有基于目标、基于过程和多点地质统计学三种方法[9-16]。基于目标的模拟方法虽然能较好地再现河道的形态，但难以准确刻画点坝[9]，为此，多位学者开展了点坝建模算法的探索性研究，主要有基于点坝空间形态的矢量静态模拟[17]，基于废弃河道与点坝位置关系的模拟[18]，还有基于沉积过程算法（Alluvsim）的应用性研究成果[19-21]，上述成果都没有涉及条件化方面的研究。其中，基于沉积过程的建模方法（Alluvsim）能够模拟曲流河的侧向迁移形成点坝，主要通过对曲流河中线进行随机游走实现河道的侧向迁移、垂向加积、分汊改道和决口等过程，并用几何形态参数对曲流河中线上所有的节点赋值，建立每期曲流河的三维模型，最终实现曲流河模拟，可以比较真实精细地刻画河道及点坝的几何形态[10]。条件化是基于目标和基于过程的建模方法待解决的另一个难题，即建立的模型不能很好地满足井点条件[14,20,22]，难以满足实际工作需要；多点地质统计学由于训练图像平稳性问题多存在模拟不完全的现象，如模拟的河道易出现中断[23-29]。可见，传统建模方法难以做到既有效描述点坝与河流形态，又满足井点条件，因此需要开展更深层次的研究。

近年来，随着人工智能技术的快速发展，深度学习技术在图像识别、图像生成等领域取得了突破性的进展[30-32]，其中图像的识别与生成是应用相对较广的一项技术[33-36]。图像生成主要利用生成对抗网络（Generative Adversarial Networks，GAN）来进行，通过分析多幅图像，感知几何特征，进而模仿并生成相关图像，该算法自2014 年Goodfellowet al.[37]提出以来，在地质研究上被广泛应用于生成各种复杂图像，例如：岩石薄片图像生成、数字岩心重构等[38-41]。这些人工智能生成的图像细节丰富、逼真，为模拟复杂多变的曲流河带来了可能。已有学者在人工智能曲流河建模方面做了一些探索性的工作：如利用生成对抗网络生成无条件化的二维[42]和三维曲流河图像[43]；为了解决条件化的难题，一些学者提出了多种解决方案：主要有条件化井数据[44-45]、分层训练[46]、样本参数化[47]等方法，成功生成了条件化的三维曲流河模型，但这些模型没有考虑点坝砂体，也没有采用实际数据对模型进行验证。期望克服以上不足，实现以下目标：建立一个既能满足井点条件，又具有一定预测效果的三维曲流河与点坝模型。

以鄂尔多斯盆地某气田为研究对象，采用条件生成对抗网络算法进行曲流河建模。为了较好地模拟点坝砂体，采用Alluvsim 算法建立多个（200）能够反映研究区曲流河弯曲形态以及点坝砂体的模型，通过卷积神经网络对200 个模型进行深度学习获取特征矩阵，在此基础上，结合实际井点数据利用条件生成对抗网络来生成曲流河模型，从而实现模拟结果既能很好地刻画点坝及曲流河弯曲形态，又能很好地满足井点条件。同时，详细讨论了影响模拟结果的关键因素，将模拟结果与多点地质统计学建模结果对比分析，并进行了模型的抽稀井检验。

1 生成对抗网络原理

生成对抗网络是一种基于深度学习的生成模型，由Goodfellowet al.[37]在2014 年提出，是近年来复杂分布上无监督学习最具前景的方法之一，主要应用于图像生成领域。与传统深度学习算法不同，它主要根据生成器与判别器之间的“博弈”对生成结果不断优化。在这个“博弈”过程中，生成器的目标是建立模型，判别器的目标是判别模型的真伪。为了在“博弈”过程中取得成功，生成器必须学习建立能够反映地质特征的模型，而判别器则会通过不断地判别模型的真伪来提高判别能力，通过不断地建立与判别，直到判别器无法识别生成模型的真伪，这时生成器就可以建立可靠合理的模型。

假设用于训练的模型数据为x，模型数据的分布为Pdata（x），随机变量z的分布为Pz(z)，在理想情况下G(z)的分布应该尽可能地接近Pdata(x)。根据交叉熵损失，可以构造损失函数：

式中：EX～Pdata(x)[·]与EZ～PZ(Z)[·]指数学期望，EX～Pdata(x)是在训练数据x 中取得的样本，EZ～PZ(Z)是从随机变量z 中取得的样本。其中G(z)代表生成器G 生成的模型，D(x)代表判别器D判断模型是否真实的概率；D(G(z))是判别器D判断G(z)是否真实的概率。

通过GAN网络训练得到的模型可以随机生成河道砂体模型，但是与基于目标的模拟方法一样难以条件化，所以需要在这一过程中加入一定的约束条件，使生成器能够生成满足井点条件的模型。

为了解决这一问题，有学者在GAN 的基础上提出了CGAN（Conditional Generative Adversarial Networks）模型[48]，在训练与生成过程中加入约束条件y，即在公式1中加入条件y（井点数据）：

式中：D(x|y)为判别器输出的模型x是否是条件y所对应模型的概率；G(z|y)为随机向量z在该条件y下生成的模型。

在训练过程中，需要在给定条件下将生成的模型与实际的模型做对比，所以在训练时需要输入成对的训练集。利用公式（2）建立了新的损失函数：

式中：y表示条件数据，x为训练数据，z为输入G网络的随机向量，G（z|y）为G网络根据条件数据和随机向量生成的目标模型，D（y,G（z|y））是D 网络判断G 生成的模型在y条件下是否真实的概率。

数据集异常值、网络参数以及损失函数的设定不当通常会影响模型训练的效果，过拟合是在模型训练过程中最常出现的现象，在本次训练过程中也遇到了这种现象，很多学者提出了各种方法来解决这一问题[49-52]，其中利用正则化惩罚项是最常见的手段，本研究采用L2 正则化惩罚项来解决这一问题，即：

式中：w为网络中所用到的权重参数，λ是控制L2（G）比例的超参数，本研究设定为0.001。L2可以加快模型收敛并提高模型的精度。因最终目标是形成一个生成满足井点条件河道模型的生成网络，最终的目标函数为：

式中：输入模型x（训练集）与条件y（条件集），判别网络提取训练集与条件集的特征矩阵，并通过两个全连接层得到训练模型的真实概率；生成网络中的Encoder（编码器）将条件y 进行下采样提取条件特征，结合随机噪音数据输入到Decoder（解码器）中生成满足条件y的模型；将生成的模型输入判别网络得到模型是否真实的概率，并与训练数据的概率进行对比；将对比结果反馈给生成对抗网络并进行参数优化，通过多次迭代使损失函数G*趋于稳定时就可以得到能生成满足研究区条件曲流河模型的生成网络（公式5）。

2 基于生成对抗网络的建模方法

与传统建模方法不同，基于生成对抗网络的建模是模拟人脑的思维过程，它需要对同类型的模型不断学习、模仿，从而提高建模（模仿）水平，最终能够建立（模仿）一个形态特征与学习数据一致、与实际钻井吻合的模型。

在上述建模实现过程中主要有以下四个步骤（其中②、③、④是交叉迭代进行的），图1为建模过程流程图。

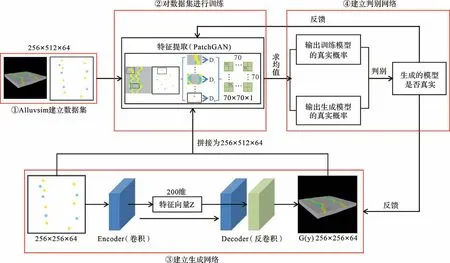
图1 基于生成对抗网络的曲流河建模流程图Fig.1 Flow chart of meandering river modeling based on the generated countermeasure network

1）准备用于深度学习的模型——训练数据的建立方法

CGAN理论的核心在于对数据开展深度学习，这就需要采用合适的方法建立一定数量的能够反映研究区砂体空间形态特征的地质模型。

点坝是曲流河沉积单元中最重要的储集砂体，也是研究区的重点研究对象，因此建立的模型不仅要很好地再现曲流河的弯曲形态，还要能够在成因上反映点坝砂体的空间形态。

尽管基于目标的建模方法能较好刻画河流弯曲形态，但难以刻画点坝[9]，多点地质统计学则难以刻画连续形态的河道[23-29]。基于以上不足，Pyrczet al.[10]在2009 年提出了基于沉积过程的建模方法（Alluvsim），Alluvsim能够模拟河道的侧向迁移，从而较好地在河道的凹岸加积形成点坝，国内多位学者开展了利用Alluvsim 算法模拟点坝砂体的研究[18-21]。因而Alluvsim建立的模型符合研究区砂体特征，是本文建立数据集所采用的方法。

Alluvsim的主要输入参数为河道平均厚度、河道宽厚比、河道弯曲度、模拟河道的条数。设定好这些初始参数，即可开展Alluvsim 随机模拟，得到多个曲流河砂体模型，用于下一步的深度学习。

2）对①的模型进行深度学习——数据集的训练方法

人工智能是模仿人脑学习的过程，在建立河道模型之前必须先对模型进行学习，因此特征的提取尤为重要。研究区模型的厚度为30 m，为了保证模型的精度，垂向能达到每个网格0.5 m 的精度（多数开发阶段地质建模所采用的精度），同时便于计算机计算，网格数量设置为2的倍数，垂向网格设置为64个。横向尺寸考虑到满足模型的精度和计算机的数据处理能力，设置为256，最终训练模型的网格大小为256×256×64（共419 万个网格），第一层卷积核定义为3×3×64的矩阵。

特征提取主要通过卷积神经网络来进行，采用PatchGAN结构[53]，对于三维地质模型，需将一个模型分解为N×N 个部分，每部分通过多个卷积层，得到N×N×1 的判别层，其中每个元素代表对应的真伪判定结果，整个输入的真伪判定结果是N×N 个元素的均值，经过Isolaet al.[53]的研究，将N设为70模型生成效果最好，本文也采用这一参数。

通过大量的卷积核对上一层的模型进行卷积运算，在①的模型中提取出了大量的特征矩阵。在特征提取过程中，需要将每层模型的值（每个网格单元）与卷积核进行线性运算（y=w×x+b，w 为卷积核的参数，b 为偏置项）。由于池化层对上一层的输出信息有一定的“舍弃”，会丢失一定的信息，但并不能保证所舍弃的信息是否有用，故在研究中用卷积层来代替池化层，保证神经网络可以获取更多的信息。在训练时会通过梯度下降法不断优化w和b，因而每一个卷积层输出的特征都是原始模型在该隐空间上的映射，而提取到的特征矩阵会在训练过程中随着优化而不断变化。在上述特征提取步骤中，为了使生成的模型满足给定的井点条件，需要将训练模型与条件模型在相同维度上进行拼接，即河道模型与条件模型的大小为256×256×64，拼接之后的模型大小则为256×512×64（图2）。

图2 训练模型与条件模型拼接示意图Fig.2 Schematic diagram of training and conditional model splicing

3）在深度学习的基础上开始模仿①的模型进行建模——生成网络的建立方法

模型的生成（建立）则是②的逆过程，目前应用较广的是采用U-Net 结构[53]来生成模型，它主要是通过对特征矩阵进行相同层数的反卷积运算实现。在反卷积过程中，模型的生成（生成网络来实现）与对比（判别网络来实现）以及模型的训练（深度学习）在运算过程中是交叉运行的。

CGAN模型主体为判别网络与生成网络，判别网络主要对模型进行特征提取，并判断模型的真实性；生成网络主要采用U-Net网络结构，生成网络需要将条件模型进行卷积操作（Encoder 过程）生成特征向量，然后对特征向量进行反卷积（Decoder 过程）生成对应的三维模型。

在U-Net 结构中，Encoder（编码器）为一个深度卷积神经网络，将条件数据通过多层卷积运算进行下采样，提取井点数据信息。在研究中将Encoder过程设定为6 个卷积层，卷积核计算步幅设定为2，卷积核个数由浅入深分别设定为32，64，128，256，512与1 024个，最终得到一个4×4×1 024的矩阵，通过两个全连接层将该矩阵输出为一个100 个数据的一维向量，然后再建立一个100个数据的服从正态分布的一维随机数组，将两个数组拼接为一个200个数据的一维数组，得到一个随机向量；Decoder（解码器）为反卷积过程，通过结合Encoder过程所采集到的各层信息以及与Encoder过程相同层数的反卷积层运算，即Encoder 的逆过程，生成一个模型。判别所生成模型在条件数据下的真实性，然后输出损失函数的变化曲线，当该曲线随训练的进行趋于稳定时，CGAN 模型就已经训练完成。将每个模型的权重、损失量等信息反馈给生成网络与判别网络，根据反馈信息调整参数，使生成网络生成的每一个模型越来越接近训练数据。

4）对③所建立的模型与①的模型进行对比——判别网络的建立方法

训练模型中真实模型的概率：将②中训练模型所提取到的特征值，通过两个全连接层网络输出一个模型是否为真实的概率值（模型的真实与否，在训练模型中需预先标定）。

生成模型是否真实的概率：将③中所建立的模型提取特征矩阵后，同样通过两个全连接层输出概率值。

生成模型的对比：将“生成模型是否真实的概率”与“训练模型中真实模型的概率”进行对比，从而得到生成模型是否真实的结果。

3 建模实例研究

3.1 工区概况

研究区位于苏里格气田南部地区（图3a），伊陕斜坡西部中段，坡降非常平缓，为3～5 m/km，地层倾角不足1°。上古生界石盒子组盒8 段是本区的主力含气层段，该段砂体分布稳定，含气性好，具有较大的勘探和开发潜力。盒8段平均孔隙度较低，集中在5%～8%，属于低孔储层。图3b为长庆油田内部沉积相研究成果，建模工区位于图3b中西侧，前人研究成果显示建模工区内分布有两条曲流河，工区面积为25 km2，钻井较少共有10口井，研究目的层为盒8上1段，前人研究成果显示邻区盒8上段均为曲流河沉积环境[54-58]，本区岩心与测井显示为曲流河河道的沉积特征（图4，5）。

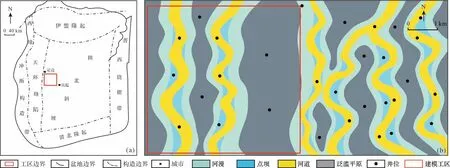
图3 研究工区概况（a）研究区位置图；（b）研究区沉积相（长庆油田内部成果）Fig.3 Overview of the study area

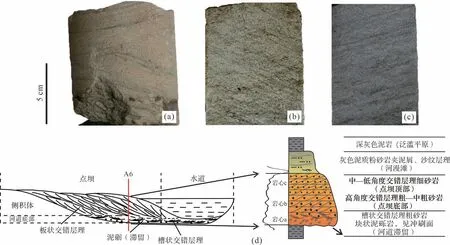
图4 研究区A6 井曲流河沉积特征（a）1 498.65 m，上部为灰色粗—中砂岩，槽状交错层理，下部部见冲刷面、滞留泥砾；（b）1 492.32 m，灰色粗—中砂岩，厚层状，可见多组高角度板状交错层理；（c）1 484.83 m，浅灰绿色细砂岩，厚层状，可见多组中—低角度板状交错层理；（d）曲流河沉积剖面与垂向沉积序列图Fig.4 Sedimentary characteristics of meandering river in well A6 in the study area(a) 1 498.65 m,the upper part is gray coarse medium sandstone with trough cross bedding,and the lower part is the scouring surface and retained mud gravel;(b) 1 492.32 m,bray coarse medium sandstone with thick layer,with multiple groups of high angle plate cross bedding visible;(c) 1 484.83 m,light gray green fine sandstone with thick layer,with multiple groups of medium low angle plate cross bedding visible

图4a岩心上部为灰色粗砂岩，槽状交错层理，反映河道沉积特征；下部见冲刷面，滞留砾岩，反映了河床底部的冲刷沉积特征。图4b岩心为浅灰绿色细砂岩，厚层状，可见多组高角度板状交错层理，反映了层理角度较大的点坝底部侧向加积的沉积特征。图4c岩心位于点坝侧积体顶部，相对图4b的岩心层理角度变小，粒度变细。河道在侧向迁移的过程中，每一期侧移层底部为河床滞留沉积，滞留沉积之上为槽状交错层理，侧向迁移形成的点坝主体则是板状交错层理，A6 井属于沉积序列中的点坝主体（图4d）。

自然伽马（GR）测井曲线的形态整体显示出正旋回的沉积特征（图5），其中A5整体砂岩厚度较大，GR整体值偏低，为点坝沉积特征；A1～A4正旋回现象较明显，下部GR值低，上部GR值高，反映了河道侧积过程中河道与点坝的复合沉积，A1-A4井整体下部低GR曲线段为点坝沉积，上部高GR曲线段为河道沉积。

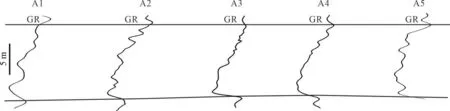
图5 层GR 曲线沉积特征（以正旋回沉积为主）Fig.5 Sedimentary characteristics of the gamma ray (GR) curve from (primarily positive cycle sedimentation)

3.2 建模输入参数

1）Alluvsim模型的建立

因研究受国家自然科学基金项目资助，属于探索性研究，为了明确方法的可行性以及能够较好地体现研究效果，选取了面积和地层厚度相对较小的工区来开展研究（不考虑河漫沉积，以模拟满足井点条件的点坝和河道为主），工区内沉积体也相对简单，分布有2 条曲流河（图3b）。研究的训练模型数据集利用Pyrczet al.[10]公开发表的Alluvsim源代码建立，该源代码采用Fortran 语言编译，利用Petrel 建模软件对成果进行三维显示。基于Alluvsim 算法建立了200个河道砂体等概率模型（图6），模型的网格尺寸为5 km×5 km×30 m。Alluvsim 算法是基于河道沉积过程的算法，只需输入河道相关参数即可得到对应的模型，根据图3b前人沉积相研究成果，统计得到河道弯曲度为1.4，河道的平均宽度为500 m，根据测井曲线统计得到河道的平均厚度为12 m，河道宽厚比设置为45，模拟河道条数为2。图6的模拟结果中黄色为河道，蓝色为点坝，灰色为泛滥平原沉积（泥岩为主），模拟出的河道在剖面上呈正透镜状，河道改道弯曲的区域则是点坝砂体，较好地体现了河道及点坝的沉积特征。

图6 训练用模型（显示了16 个）Fig.6 Models used for training (16 shown)

Alluvsim在建立河道模型过程中，通过将河道在空间上进行平移以满足井数据。因初始构建的河道模型未考虑任何井点数据，在河道平移的过程中，常出现难以满足所有井点的现象，从而造成模型条件化程度低、不收敛，甚至崩溃。基于此，研究采用条件生成对抗网络（CGAN）的建模思路来解决条件化的难题。生成对抗网络（GAN）是在随机噪音的基础上生成模型，而CGAN 所采用的随机噪音模型中则包含了井点数据作为初始数据，因而生成的模型能与井点数据吻合较好。若在对200 个模型训练时均采用实际井点数据作为条件数据，那么在生成模型时，一旦实际建模时井点数据发生了变化（如新增加钻井），可能造成生成的模型条件化效果不高，也即该训练模型仅适用于工区目前的井点分布情况。一旦建模时井点分布发生变化，则需要根据实际井点数据重新训练，会耗费大量机时。为了应对不同的井点分布情况，需要随机设定井位分布，即让模型训练时能考虑足够多的可能性，这样训练完毕的模型适用性也更广。这也是深度学习的主要特点，需要足够多的随机样本（训练模型、条件模型）进行学习，增强模型的生成能力。

根据图5的模型随机设定了相应的井点条件（图7），即基于训练模型集中的每个模型（200 个），随机设定一些虚拟井，每口井有着与模型对应位置的微相特征，其中泛滥平原作为背景相输入，条件相为河道与点坝。该条件模型同样为三维模型，垂向上分为64 个网格单元层，每一网格层的条件与建立的三维河道砂体模型的每一网格层模型一一对应。为了确保建立模型时能够满足实际井点条件，训练时的条件井数应大于实际井数，因而在图7中训练用的井数大于10（随机设定井数为11、12、13）。图8为工区实际井点数据，本次参与模拟的井共10口，作为生成该河道砂体模型的条件数据。其中钻遇以河道为主的井4 口，钻遇以点坝为主的井2 口，钻遇以泛滥平原泥岩为主的井4 口。基于以上数据开展了深度学习，期望所建立的河道模型能够再现砂体的复杂形态，并较好地满足井点条件。

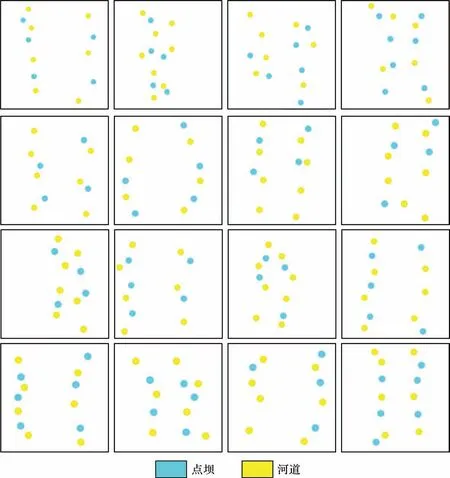
图7 条件数据（显示了16 个）Fig.7 Condition data (16 shown)

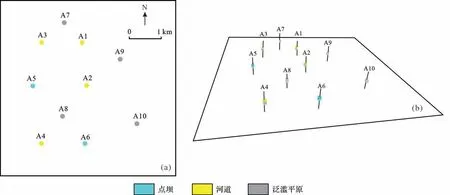
图8 研究区井点数据（a）井点位置平面图；（b）井点数据三维图Fig.8 Well point data in the study area

3.3 建模结果

CGAN网络的训练利用Mirzaet al.[48]公开发表的源代码进行二次开发并建立，该源代码采用Python语言编译，利用Petrel 建模软件对成果进行三维显示。

在数据集的训练过程中，理论上训练次数越多，提取的特征矩阵也会越多，从而保证生成模型的质量。研究将图6 与图7 作为“数据对”训练100次，以图7 作为条件数据，建立了该工区的三维河道模型。

为了展示模型中河道的垂向变化，图9为该模型第1、15、30、40个网格层的二维模型。模拟结果再现了弯曲的河道，也基本体现了河道与点坝的形态及相互关系。图9a～d显示了河道在垂向上由河道顶部到底部的变化特征，由于河道形态呈正透镜状，从顶到底河道整体的宽度应逐渐变窄。

图9 训练100 次时各网格层的模型Fig.9 Model of each grid layer after training 100 times

在图9中，图b与图a对应较好，可以展示点坝及河道垂向上的变化；图c左侧标注区的点坝与图a、b、d没有对应关系，右侧标注区与图a、b对应较差，图c北部河道与点坝的形状和规模也不符合河道的垂向变化特征；与图a、b、c 相比，图d 标注区的河道弯曲度较小，导致河道形状及点坝个数与图a、b、c在垂向上对应关系较差。

上述分析说明该模型在每一个网格层模拟效果较好，垂向上也可以展示河道的变化特征，但模型在三维空间上存在河道形状、点坝个数不对应的现象，不能体现河道的沉积成因及变化规律。

4 讨论

为了明确影响模型结果的关键因素，并提高模型的精度，从以下几方面开展了讨论。

4.1 输入参数

由于CGAN模型输入参数较多，鉴于CGAN目前应用较广，为相对较成熟的算法，一一测试不仅耗费大量机时，还占用大量篇幅，故研究中的各个参数均为经验取值，因最终的建模结果能够满足研究的需求，没有对输入参数做进一步的测试，表1 为研究过程中CGAN的主要参数及意义。

4.2 训练次数

本次测试在训练集模型数量为200的前提下，分别通过训练10 次、50 次、100 次以及200 次建立四个生成器，将图7的条件数据分别输入四个生成器中生成四个模型，与图9一样，输出第1、15、30、40网格层的二维模型来展示模型特征。由于河道形态在垂向上是变化的，在顶面规模最大、底面最小，因而图10～12的结果中，最上面的网格层（第1层，河道顶面）与井点吻合很好；由于钻井并不总是位于河道最厚处，随着网格层向河道底部移动，会出现一些偏差，主要集中在河道底部的第40 个网格层。整体上，随着训练次数的增加，生成的模型与井点吻合度越来越高（图10～12）。

当训练10 次时（图10），单层模型河道形态基本展现出来，但部分区域模拟不完整，河道存在中断的现象；点坝基本在河道弯曲处生成，形态还需要进一步优化。垂向上也能体现河道及点坝的变化，即由顶到底河道宽度逐渐变窄，点坝规模逐渐变小，但某些部位与上下层的对应关系较差（标注区的河道弯曲度及点坝的位置、大小）。

当训练50 次时（图11），单层模型河道形态变好，河道的形态也更为连续，局部还有断开的现象。模型中部模拟较好，南北两侧模拟较差，细节刻画还不够精确；点坝模拟则较为完整，但图11a 下部、图11c 上部等某些部位与河道之间的对应关系较差。垂向上与图10 相比更能体现河道及点坝的垂向变化，但某些河道的几何形态上下层不一致（标注区）。

图11 训练50 次时各网格层的模型图（a）第1层；（b）第15层；（c）第30层；（d）第40层Fig.11 Model of each grid layer after training 50 times

当训练100 次时（图9），河道的连续性，点坝与河道的关系模拟较为合理，除垂向各层之间河道及点坝的几何形状、大小及对应关系还有待完善，模型基本满足曲流河沉积特征。

当训练200 次时（图12），各单层模型模拟较为完全，河道连续，点坝的形状、大小与位置正确，河道与点坝的对应关系也较好。垂向上各单层体现出河道及点坝的变化，即从顶到底河道宽度及点坝大小逐渐变小，图9～11 中上下层不对应的情况也得到了很好的解决。将得到的曲流河砂体三维模型数据输入Petrel 软件中得到该工区的地质模型可视化图（图13）。

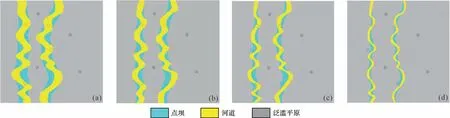
图12 训练200 次时各层的模型图（a）第1层；（b）第15层；（c）第30层；（d）第40层Fig.12 Model of each layer after training 200 times

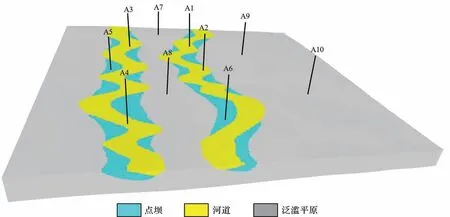
图13 工区三维河道地质模型Fig.13 Three-dimensional (3D) river geological model of the study area

上述测试说明更多的训练次数会带来更好的模拟结果，但相应的计算时间会成倍增加，为了确定最优化的训练次数，在训练过程中统计了G*损失函数的值。图14显示损失函数随着训练次数的增加逐渐降低，并逐渐收敛于0.7，当训练次数为160时，损失函数的值保持稳定，说明更多的训练次数不能带来更好的模拟效果，因此本工区最合适的训练次数为160。

图14 G*损失函数变化曲线图Fig.14 Variation of G* loss function

4.3 数据集的影响

深度学习的基础是训练数据集，为了确定最优化的数据集数量，本次研究分别使用10、50、100、200个模型数量来进行训练，将图8条件数据分别输入生成器得到4 个模型，同样输出每个模型的第1、15、30、40网格层二维模型进行对比。

上述的10、50、100、200 个模型均由Alluvsim 建立，这些模型主要用于深度学习，理论上来说用于学习的模型数量越多，最后生成的模型越真实（如同学习画，临摹的数量越多，画出成品的概率越高），但模型数量并不是越多越好，模型数量越多意味着更多的运算时间，需要找到适合工区的最优化学习模型的数量。

以下4 次测试均为模型训练本研究区最优化的训练次数（160次）。

当训练10 个模型时，如图15 所示，生成的模型没有展现曲流河的形态，仅在井点数据周围生成了一些数据，河道不仅连续性差且看不出河道与点坝的关系，模拟的效果非常差。

图15 训练10 个数据集时各层的模型图（a）第1层；（b）第15层；（c）第30层；（d）第40层Fig.15 Model of each layer for 10 training datasets

当训练50 个模型时，生成的曲流河各层模型如图16所示。平面上，各层的河道基本连续了起来，部分区域存在断开和模拟不完全的现象；垂向上，有点坝大小及河道宽度逐渐降低的趋势，但各层模型点坝与河道的几何形态对应关系较差。

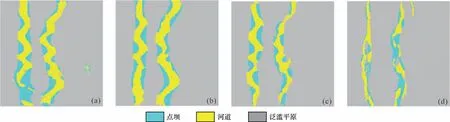
图16 训练50 个数据集时各层的模型图（a）第1层；（b）第15层；（c）第30层；（d）第40层Fig.16 Model of each layer for 50 training datasets

当训练100个模型时，所生成的曲流河各层模型如图17所示。平面上，各层模型河道基本连续，河道还存在断开的现象，一些点坝模拟效果较差，点坝与河道的对应关系较差；垂向上，基本可以体现出点坝大小与河道宽度逐渐减小的趋势，但是部分区域点坝与河道的几何形态在垂向上难以对应，由于训练数据集的增加，模拟结果与图16 相比得到了一定的改善。

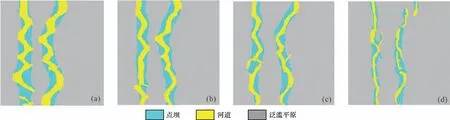
图17 训练100 个数据集时各层的模型图（a）第1层；（b）第15层；（c）第30层；（d）第40层Fig.17 Model of each layer for 100 training datasets

当训练200个模型时，所生成的曲流河各层模型如图12、13 所示。平面和垂向上模型模拟得较为完整，说明形成的生成对抗网络模型捕捉了足够多的曲流河沉积特征，通过200次的训练所建立的生成器能生成细节足够丰富，点坝与河道较为完整的曲流河砂体三维储层模型。

人工智能深度学习需要对数据样本进行大量的矩阵运算，GPU（显卡）因为其处理矩阵计算的高效性被广泛运用到深度学习，本研究在训练过程中采用英伟达的GeForce GTX 1660 型号GPU，该GPU 有1 408个流处理器单元，训练的模型大小为256×256×64，根据本文讨论的参数，训练200个模型、训练200次所花费的时间为4 h。

4.4 与传统建模方法的对比

为了体现本研究所建模型方法的适用性，与传统建模方法进行了对比。其中基于目标的模拟目前难以很好地刻画点坝，另外目前河道建模条件化所采用的方法为先模拟河道，再对河道进行平移或旋转等来满足井点条件，在这个过程中通常会出现河道形态扭曲和不能满足所有井点的现象，造成基于目标的建模方法难以应用于实际工作中。

图13显示本文所采用的方法与序贯指示模拟方法类似，为基于已知数据进行河道模拟，从而能完全满足井点条件，进一步通过深度学习再现河道和点坝的形态。与基于目标的方法相比，本文所采用的方法不仅能很好地模拟河道和点坝的形态，也能很好地条件化，即生成的模型与井点数据是完全吻合的（图8、图18a）。

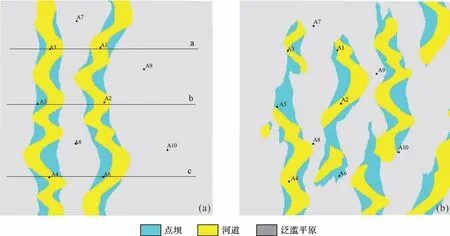
图18 人工智能生成模型与多点地质统计学模拟结果对比（a）人工智能生成模型；（b）多点地质统计学模拟结果Fig.18 Comparison between artificial intelligence generation model and multipoint geostatistical simulation results

多点地质统计学可以模拟复杂储层形态及其相互关系，为此，本研究仅将CGAN 模拟结果与多点地质统计学的模拟结果进行对比分析，在多点地质统计学模拟中所采用的训练图像为图18a的成果。

通过对比图18 的模拟结果可知，因采用图18a作为训练图像，图18b的多点地质统计学模拟的结果首先能满足井点条件，其次较好地反映了点坝与河道之间的关系，这是多点地质统计学的优势；但同时图18b 对河道的连续性模拟得并不好，存在多处中断，多位学者的研究也证实了这点[23-29]，并且模拟结果中出现了大约4条主河道，而训练图像中仅给出了2 条河道，并不能很好地再现图18a 中的沉积特征。对比结果表明与传统建模方法相比，本文所采用的方法能较好地再现河道模型地质体的空间特征。

同时图18a的模拟结果也较好地体现了图3b中的河道沉积特征，主要分布有2 条河道，河道弯曲的区域分布有点坝，河道与点坝的规模与前人的研究成果也相符合，且实现了河道储层的三维化，能在此基础上开展更为精细的描述（本研究中未考虑河漫沉积）。

4.5 模型的验证

为了检验所建立的模型是否能够准确表征砂体的特征，通常采用抽稀井检验、油藏数值模拟检验等方法。油藏数值模拟适用于开发中的油气田，故而本研究区主要采用抽稀井检验的方法。因模型的主要目的是刻画点坝砂体，为了检验模型的预测精度，依据实际井钻遇砂体情况，将图8中的A5井去掉，将剩下的A1～A4、A6～A10 作为条件数据输入到CGAN网络，建立了基于9口井的河道模型，以检验A5井处的点坝预测效果。

图19 为模拟结果，可以发现整体结果与图18a差异不大。右侧河道区域由于没有对井数进行改变，模拟结果保持不变；左侧河道在模拟过程中参与计算的为A3、A4两口井，整体形态与分布变化不大，变化的区域主要体现在A3 与A4 两口井之间的河道区域，与图18a相比较，由于条件数据更少（图18a为3 口井，图19 为2 口井），对模拟结果的约束也就越少，因而模拟的河道形态更为均匀、协调（河道宽度变化较小，主要体现在河道的波峰波谷位置），A5 井区的点坝也得到了很好的预测，与井点吻合较好。

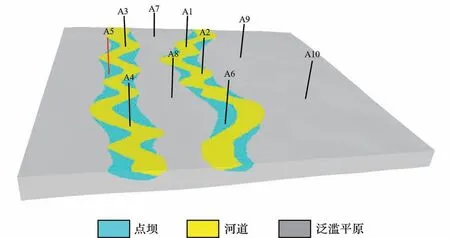
图19 模型抽稀井验证（A5 为抽稀井）Fig.19 Verification of model dilution well (A5)

为了更清晰地明确河道的演化，选取了3条过井剖面（图18a）。可以很清晰地显示河道内部沉积特征，整体上与测井曲线吻合较好，其中点坝以砂为主，对应测井曲线低GR部分；河道以细粒沉积为主，对应测井曲线的上部高GR 值（图20）。也说明了本文所采取的研究方法能有效进行河道沉积砂体的模拟，利用图19 的三维地质模型可以开展进一步的有利储层研究。

图20 过井剖面图Fig.20 Cross-sections

5 结论与展望

针对传统的建模方法难以有效模拟曲流河砂体，本文利用基于人工智能深度学习的条件生成对抗网络（CGAN），克服了其他建模方法的条件化困难、不易恢复点坝砂体等难题，在河道人工智能三维建模方面进行了深入研究。

本研究通过Alluvsim 算法建立了200 个反映目标区河流沉积特征的三维模型，通过大量的卷积运算提取河道模型训练数据集的特征矩阵，利用条件生成对抗网络（CGAN）建立了可以生成河道砂体三维模型的生成网络，通过反卷积操作来生成所需的河道模型，所建立的模型可以很好地克服传统建模方法的不足。在模拟地质体形态方面，由于模拟结果是在对大量Alluvsim 模型（包含点坝与曲流河）深度学习基础上利用条件生成对抗网络所生成的，模拟的曲流河与点坝形态特征与训练数据（Alluvsim模型）保持一致，这也是生成网络的优势；在条件化方面，因在生成过程中加入了条件数据的约束，生成网络模拟的结果除了能与Alluvsim模型保持一致，还会满足实际井点数据，打破了长久以来传统曲流河建模方法条件化困难的局面，从而使得建立的曲流河模型能与实际更有效地结合。

研究表明，训练时所用的学习数据越多，模型在深度学习的过程中所提取的信息也越多，在模型生成阶段根据条件数据所建立的模型也越可靠。而在给定训练数据集的前提下，该算法对模型训练的次数愈多，所获得的模型特征数据库愈大，所包含的模型细节也愈丰富，生成的模型也愈反映输入模型的形态特征。

虽然本文的研究取得了一定的效果，目前国内应用Alluvsim 算法研究曲流河建模的主要是高校多年研究建模算法的科研工作者，主要采用研究源代码的方式，如何降低建立训练模型的门槛，可能是曲流河人工智能建模今后要考虑的方向。

另外三角洲沉积砂体规模大，是近年致密油气勘探的重要领域，与曲流河相比，三角洲沉积受河湖交互影响，砂体的空间分布更为复杂，难以较好地随机模拟三角洲及内部砂体的形态及分布。现阶段能反映各微相三维特征的三角洲训练模型多为手动修改完成，这对需要大量训练数据的人工智能建模研究来说是巨大的工作量，利用多点地质统计学采用人机互动的方式建立三角洲训练模型是一个较为可行的策略，作者正在这方面开展积极的探索研究。

相信随着计算机软硬件技术的快速发展，能更好地拓宽人工智能地质建模的应用领域，为今后智能化油气田的勘探和开发添砖加瓦。