单轴压缩条件下裂隙几何特征对岩石力学特性的影响研究*

周立,李杨,廖超龙,夏文浩,张理

(1.广西高峰矿业有限责任公司,广西 南丹县 547205;2.北京科技大学 土木与资源工程学院,北京 100083)

0 引言

裂隙岩体是一类复杂的工程介质,其广泛存在于水利水电、采矿、石油开采、国防建设等工程中[1]。裂隙岩体内部包含着断层、节理等各种软弱结构面,其几何特征对岩体的强度和变形特性有着重要的影响。因此,开展裂隙几何特征对岩体强度和变形破坏的影响研究,对保证裂隙岩体工程的安全稳定有着重要的意义。

目前,学者们大多通过理论分析、室内试验和数值模拟的方法对裂隙岩体力学性质、裂纹扩展及破坏机制等方面进行研究。仝兴华等[2]通过理论分析方法探讨了裂隙的平均间距、法向刚度和剪切刚度对裂隙岩体的峰后应力-应变曲线的影响。韩健[3]通过室内力学试验系统地研究了裂隙几何特征对裂隙岩体力学参数的影响。蒲成志、肖桃李等[4-5]通过开展单轴、三轴力学试验探究了预制2条贯通裂隙类岩石材料的破坏特性。张伟等[6]对比分析了动静载荷下倾角对裂隙岩体力学特性影响的差异。唐红梅等[7]采用RFPA 软件模拟分析了单轴条件下裂隙水平位置、倾角及长度变化对扩展角、强度、能量特征的影响。鲜振兴等[8]开展了循环荷载下单裂隙岩体疲劳损伤演化规律及模型的研究,并提出了不同单裂隙角度岩体的疲劳累积损伤模型。武东阳等[9]采用单轴压缩试验、声发射技术、数字照相技术和PFC3D 数值模拟等手段探究了锚杆和裂隙倾角对裂隙岩体的锚固效应及其对裂纹扩展的影响。莫云龙等[10]通过CT 技术重构岩石三维特征,并基于统计学原理分析了岩体物理力学特性与其原生裂隙几何特征的联系。张艳博等[11]基于RFPA 探究了裂隙几何特征对岩石峰值强度的影响。牛江伟等[12]通过室内试验和数值模拟分析了节理倾角对岩石峰值强度的影响。马平等[13]采用超细单元划分法构建模型,基于FLAC3D 软件深入探究了单轴压缩下含X 型交叉裂隙的岩体力学特性和破裂机制。

学者们大多采用PFC、RFPA、UDEC 和FLAC3D 等数值模拟软件对裂隙岩体力学特性进行分析研究,其中PFC、UDEC等离散元软件和有限元软件RFPA 具有可模拟岩石材料的断裂及裂纹发展过程的优点,但计算效率相对较低,参数校核麻烦,而FLAC3D 软件基于连续网格,采用有限差分法进行计算,相较于PFC、UDEC 和RFPA,无法较好地反映材料的断裂及裂纹发展,只能通过塑性区反映岩石破坏情况,但是其参数很容易通过常规物理试验获得,且计算参数和实际岩石物理力学参数完全对应[14],已在裂隙岩体的相关模拟中得到了较好的应用[15-17]。

因此,本文通过Rhino-Griddle软件建立不同裂隙几何特征的标准岩样数值模型,并采用FLAC3D软件对单轴压缩条件下裂隙岩体的变形破坏规律进行了模拟研究,探讨了裂隙倾角、裂隙张开度、裂隙数目等几何特征与岩石力学特性的关联,并对多裂隙岩样的裂纹扩展规律进行了研究。

1 数值计算模型

1.1 模拟方案设计

本文主要研究裂隙角度a、裂隙张开度b、裂隙数目e对单轴压缩试验中岩体力学特性的影响,分别设计了3组试验组,同时选择无裂隙岩样作为空白对照,各方案中裂隙长度(c=16 mm)和裂隙间距(d=15 mm)均保持不变,试验方案见表1和图1,裂隙几何分布如图2所示。

图1 裂隙几何特征岩样

图2 裂隙几何分布

表1 数值计算方案设计

1.2 岩样模型构建

采用Rhino建立含有不同裂隙几何特征的标准圆柱体试样模型(φ50 mm×100 mm),并通过Griddle插件将模型转换为能被FLAC3D 读取的f3grid网格文件,最后导入到FLAC3D 中进行数值计算。模型共划分为约1 141 000个单元和203 000 个节点,模型底部通过速度施加固定约束,模型顶部通过控制轴向位移的方法模拟加载过程,加载速率为1×10-7mm/step,岩样数值模型如图3所示。

图3 岩样数值模型

模型采用应变软化模型[18],应变软化模型是Mohr-Coulomb理论体系下的经典模型之一,在弹性阶段应变软化模型和摩尔-库伦模型一致,塑性屈服后岩石的黏聚力、内摩擦角等力学参数会随着塑性应变的增加而逐渐衰减,两种模型的应力-应变曲线如图4所示。

图4 摩尔-库仑模型与应变软化模型应力-应变曲线对比

岩石峰前阶段取值如下:弹性模量2.09 GPa,泊松比0.26,黏聚力3.61 MPa,内摩擦角30.36°,抗拉强度0.4 MPa。峰后软化阶段的黏聚力和内摩擦角随塑性应变的衰减规律参数见表2。

表2 岩石峰后软化阶段参数[19]

2 模拟结果分析

2.1 裂隙倾角对单轴力学特性影响

图5为无裂隙岩样和3 种不同裂隙倾角(a=0°、45°、90°)岩样的应力-应变曲线。由图5可知,不同裂隙倾角的模型在弹性阶段表现出相似的线性变化规律,而峰后阶段应力跌落明显,呈现出一定的软化和残余特征。随着裂隙倾角的增加,岩样的抗压强度、弹性模量和峰值应变均相应地变大。

图5 不同裂隙倾角岩样应力 应变曲线

图6为不同裂隙倾角的抗压强度、残余强度和峰值应变。由图6可知,无裂隙岩样的抗压强度和峰值应变最高,说明裂隙的存在降低了岩石的力学性质。在不同裂隙倾角对比中,裂隙倾角为90°的岩样与无裂隙岩样具有相近的力学性质,抗压强度达到了完整岩石的85.1%。与之相比,裂隙倾角为0°的岩样抗压强度仅为完整岩石的24.9%,说明裂隙倾角对岩石的力学性能影响程度较大,且抗压强度、残余强度和裂隙倾角呈近似线性关系,峰值应变与裂隙倾角的线性关系稍差,但仍是裂隙倾角越大,峰值应变越大。

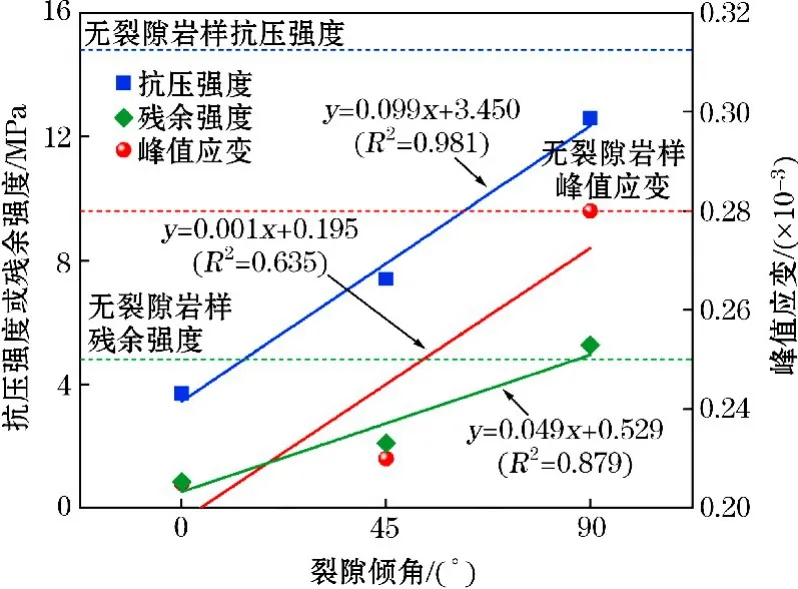
图6 不同裂隙倾角岩样抗压强度、残余强度和峰值应变

由于各方案裂隙几何特征不同,进行单轴加载时岩样的塑性区分布也有所不同,故以各方案岩样达到峰值应力时为标准,对该时刻的塑性区分布情况进行分析。其中,蓝色表示剪切破坏,红色表示拉伸破坏,黄色表示复合破坏(颜色区分见电子版)。无裂隙岩样和3种不同裂隙倾角(a=0°、45°、90°)岩样的塑性区分布如图7所示。

图7 不同裂隙倾角岩样塑性区分布

由图7可以看出,当裂隙倾角为0°和45°时,主要为拉伸破坏,且塑性区呈X 状;当裂隙倾角为90°或无裂隙时,主要为剪切破坏。由于这两种方案下岩样的抗压强度较大,加载时间较长,故塑性区不但分布在裂隙周围,在岩样端部和中部塑性区均较为发育。同时在各种倾角下,裂隙的两端均存在复合破坏区,且随着倾角的增大,复合破坏区面积不断减小。

2.2 裂隙张开度对单轴力学特性影响

图8为无裂隙岩样和3种不同裂隙张开度(b=1 mm、2 mm、3 mm)岩样的应力-应变曲线。由图8可知,裂隙张开度的增加会一定程度地削弱岩样强度,但削弱作用较为有限。

图8 不同裂隙张开度岩样应力-应变曲线

图9为不同裂隙张开度的抗压强度、残余强度和峰值应变。由图9可知,峰值应变和裂隙张开度呈近似线性关系,抗压强度与裂隙倾角的线性关系稍差,残余强度和裂隙张开度线性关系不明显。裂隙倾角为1 mm、2 mm 和3 mm 的岩样抗压强度分别为无裂隙岩石的50.1%、49.7%、45.3%,说明裂隙倾角为1 mm 和2 mm 时,对岩样力学性质的劣化程度相近,当裂隙倾角为3 mm 时,劣化程度有小幅增加。整体而言,3种张开度下岩样的抗压强度、残余强度和峰值应变差距较小,说明裂隙张开度对岩石的力学性能影响程度较为有限。

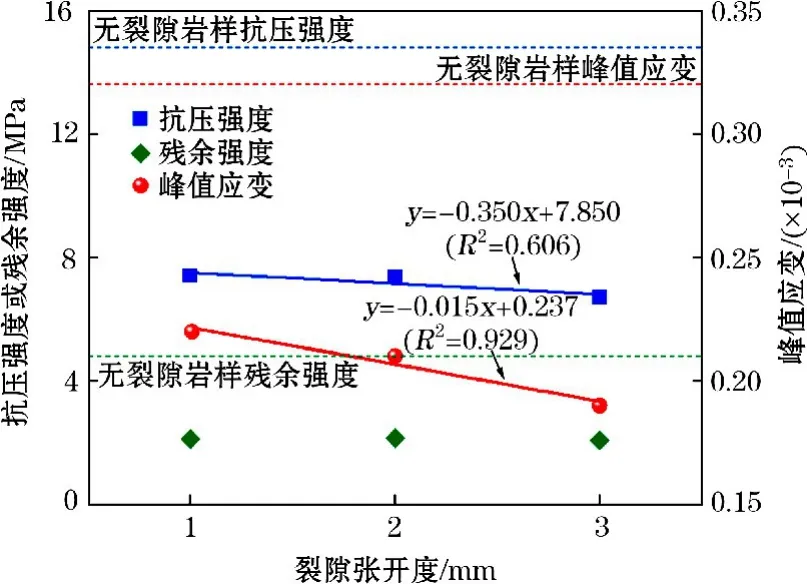
图9 不同裂隙张开度岩样抗压强度、残余强度和峰值应变

无裂隙岩样和3种不同裂隙张开度(b=1 mm、2 mm、3 mm)岩样的塑性区分布如图10所示。由图10可以看出,岩样主要为拉伸破坏,塑性区呈X状,且随着张开度的增加,拉伸破坏塑性区体积减小,裂隙两端的复合破坏区体积也有所减小,塑性区更加集中在裂隙附近。

图10 不同裂隙张开度岩样塑性区分布

2.3 裂隙数目对单轴力学特性影响

图11为无裂隙岩样和3种不同裂隙数目(e=1、2、3)岩样的应力-应变曲线,图12为不同裂隙数目的抗压强度、残余强度和峰值应变。

图11 不同裂隙数目岩样应力-应变曲线

图12 不同裂隙数目岩样抗压强度、残余强度和峰值应变

由图11可知,单裂隙和三裂隙岩样力学性质的劣化程度相近,岩样抗压强度分别为无裂隙岩石的50.1%、46.3%,与之相比,双裂隙岩样仅为29.5%,可以看出裂隙数目并不是数目越多,劣化程度越高,抗压强度、峰值应变和裂隙数目无明显的线性关系,和文献[20]结论较为一致。由图12可以看出,裂隙数目在应力-应变曲线峰后阶段的影响较为明显,单裂隙和双裂隙岩样的延性特征较为明显,但三裂隙岩样反而显示出脆性特征。同时裂隙数目越多,残余强度越低,三裂隙岩样的残余强度几乎为0。

无裂隙岩样和3种不同裂隙数目(e=1、2、3)岩样的塑性区分布如图13所示。由图13可以看出,岩样主要为拉伸破坏,裂隙数目对塑性区整体分布形态影响不大。同时塑性区从裂隙尖端发展并与邻近裂隙发生桥连,这些连接裂隙的塑性区可能会随着加载的进行继续发展贯通,使得岩样力学性质不断弱化。

3 多裂隙岩样裂纹扩展规律研究

通过对多裂隙岩样的塑性区扩展过程进行分析,以探究预制裂隙之间裂纹的发育扩展规律。由于双裂隙和三裂隙岩样的裂纹扩展规律相似,故仅以三裂隙岩样为研究对象,分别取第300,600,900,1200,1500,1800,2100,2400,2700,3000,3300,3600共12处时步下的岩样中部竖直剖面进行分析研究。其中2100时步的岩样达到峰值强度,2100 时步之前为弹性阶段,之后为塑性阶段,如图14所示。

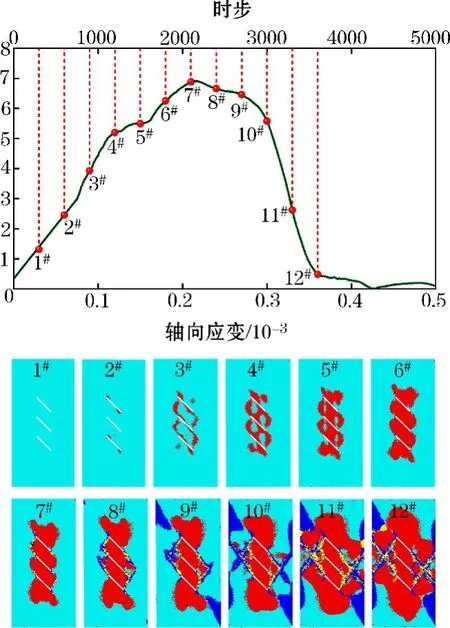
图14 三裂隙岩样各时步裂纹扩展情况

由图14可以看出,300时步(1#)岩样裂隙附近未萌生裂纹;随着加载的进行,裂隙端部出现应力集中,600时步(2#)岩样两侧的预制裂隙端部开始产生翼形裂纹,但中部预制裂隙的裂纹萌生和扩展速率较慢,此时仍未萌生裂纹。裂隙两端萌生的裂纹不仅在裂隙平行方向扩展,还沿着接近平行于轴向加载方向向其他裂隙端部扩展,900 时步(3#)岩样产生的次生裂纹不断扩展发育,直到不同预制裂隙端部裂纹上下贯通。1200时步(4#)岩样裂隙不断发育扩展,不同预制裂隙中部裂纹发生上下贯通;此后的1500时 步(5#)、1800 时 步(6#)和2100 时 步(7#)岩样裂隙继续扩展发育直到岩样破坏,预制裂隙之间裂纹发生了完全的交汇贯通。在岩石的峰后阶段,即2400时步(8#)之后的岩样裂隙端部开始出现剪切和复合裂纹,这些裂纹在预制裂隙端部发生桥连,并逐渐形成X 形破坏区,预制裂隙附近的内部裂纹也开始与外部裂纹出现扩展搭接,最终导致岩样完全失去承载能力。

4 结论

本文采用FLAC3D 对单轴压缩条件下裂隙岩体的变形破坏规律进行了模拟研究,探讨了裂隙倾角、裂隙张开度、裂隙数目与岩石单轴力学特性的关联,并对多裂隙岩样的裂纹扩展规律进行了探究,研究结论如下。

(1) 随着裂隙倾角的增加或裂隙张开度的降低,岩样的单轴抗压强度和峰值应变均有所增加,且裂隙倾角相较于裂隙张开度对岩石的力学性能影响程度更大。

(2) 裂隙数目对应力-应变曲线的影响在峰后阶段较为明显,单裂隙和双裂隙岩样的延性特征较为明显,但三裂隙岩样反而显示出脆性特征。随着裂隙数目的增加,岩样的残余强度不断降低,三裂隙岩样的残余强度几乎为0。

(3) 预制裂隙端部首先萌生裂纹,裂纹不仅向裂隙平行方向沿裂隙扩展,还沿着接近平行于轴向加载方向向其他裂隙端部扩展。次生裂纹不断扩展发育,最终导致不同预制裂隙裂纹上下完全交汇贯通,岩样达到峰值强度。峰后阶段岩样裂隙端部开始出现剪切和复合裂纹,并与外部裂纹搭接,最终导致岩样完全失去承载能力。