基于风振理论的塔式起重机非工作状态风荷载探讨
黄仕修
(海南省锅炉压力容器与特种设备检验所 海口 570102)
盘点近10年来影响我国较大的台风当数“威马逊”[1],它正面袭击海南,台风中心风力达到或超过17级,最大风力达到72 m/s。根据灾后的《海南台风塔机倒塌受损情况调查报告》[1],台风对经过地区的塔式起重机(以下称塔机)造成重大破坏,很多塔机倒塌的情况类似图1,共计143台塔机倒塌或受损。中国建筑业协会机械管理与租赁分会组织了国内部分专家和业界人士对塔机倒塌和受损情况进行了调查和分析,认为风力过大是导致以上塔机倒塌或受损的主要原因,设计标准和规范存在缺陷也是其他原因之一。海南、广东、广西、福建等沿海地区属于台风多发地区,但这些地区并未制定符合本区域气候条件的塔机准入地方标准,以至于进入这些地区的塔机不能完全满足抗风需要。建议海南相关部门收集台风和强台风登陆数据,制定符合本地区气候条件的塔机设计、制造准入地方标准。如果能通过对在超强风力作用下塔机倒塌或受损具体情况进行了解并做科学分析,从而给塔机设计、制造、使用、管理等环节提供有价值的参考意见和建议,制定有针对性的应对措施和方案,对于提高建筑起重机械行业安全管理水平将是一件有意义的事。

图1 台风引起的塔机倒塌
查询了近几年较典型的相关文献,李明等人[2]在《海南强台风塔式起重机倾覆原因分析与建议》中总结了设计上缺少理论依据、制造工艺过程存在多个环节缺陷、安装施工质量把控不严谨、现场使用管理环节落实不规范以及防风措施落实不到位等方面的问题。分析得出台风对塔机的损害原因是主观上台风风力过大,客观上设备存在缺陷。黄茂能等人[3]对厦门“莫兰蒂”台风塔式起重机倒塌情况进行调查分析,通过整理多个台风对塔机的破坏现场,也从设计、制造工艺、安装质量、使用、维护检查等方面查找问题,归纳出台风对塔机的损害原因仍然是台风风力过大,设备设计未能满足抗风要求。王玲娟等人[4]对塔机进行风振响应分析,利用有限元软件ABAQUS建立金属设计模块通过计算机模拟不同风场频率下的模拟结果,得出与塔机共振频率一致时的响应,指出塔机发生共振时的最大位移值位置。文献很少就台风最不利风载对塔机主体结构造成的耦合响应得出理论研究方向。
参考GB/T 3811—2008《起重机设计规范》[5]和GB/T 13752—2017《塔式起重机设计规范》[6]等相关标准规范,以及多篇关于风工程专著和台风对塔机造成危害的文献,对于露天作业的起重机械,如门式起重机、装卸桥、流动式起重机和门座起重机等,考虑由于附加质量较多,自振周期较同等条件的塔架要长,共振风速通常落在12~20 m/s范围内,正好是起重机械工作状态时的计算范围。处理非工作状态的风力时,计算风速内地为31 m/s(9级风力),台湾及南海为49 m/s(12级风力),共振风速远小于计算风速,这样只在下部一小部分具有共振风力,对结构受力分析不起大的影响。因此,我国现行标准对非工作状态下的起重机主体结构设计风载特性主要考虑基本风压值、风压高度变化值、迎风面积和风力系数这4个要素,顺风向利用基本风压值只考虑第一振型进行简化验算,不考虑横风共振的作用,对于塔机而言,有一定的局限性。
1 典型案例
图2记录了某台倒塌塔机最后一次摇摆过程。这台塔机由于锁住了回转装置,上机体无法随着风向的改变而转动,最能反映出台风风载中所受荷载与时间的关系。反复观察其倒塌过程,该塔机最后一次摇摆经历了逆风左摆、回到平衡位置、顺风右摆、最高附着装置失效、继续右摆、次高附着装置失效,最后整体倒塌的过程。

图2 强迫风振中的塔机摇摆
从力学分析知道,塔机最高附着装置以上机体摇摆,受到塔身弹性回复力作用,回弹力和它离开平衡位置的位移(即振幅)成正比,可以表达为F=-kx。这台塔机在向右摇摆到振幅最大位置过程中,最高附着装置提供的反力不足以克服风载荷和因风振产生的冲击力导致最终破坏。塔身标准节将所有动能继续向下一个附着装置传递,欲重新建立起新的振动模式,但最终因机体接受了更多风载动能,振幅进一步加大,对这道附着装置的冲击力更大而导致接连失效,很快发展为整机倒塌事故。
通过观察建筑工地多个台风导致塔机倒塌的过程,发现这些塔机都是因为发生了强烈的受迫振动。特别是倒塌前的阵风叠加效应,更是加快了倒塌。为了从台风风场作用时间上直接反映出台风特殊风场与塔机振幅的关系,下面利用一个简单且灵敏度较高的单摆装置进行情景模拟。
2 风振实验
参考实际台风风场做以下假设:设塔式起重机的上机体质量集中于一理想质点(质量为m);受到塔身标准节结构弹性提供的弹力为-kx;在摇摆振动中,除受台风顺风向基本风阻尼力为-c(dx/dt)的作用外,还受到台风策动力F0cosωt的作用(F0是策动力最大值,ω为策动力角频率)。参考《风工程与结构抗风设计》[7]中风振计算方法,根据牛顿第二定律,可得式(1)。
令ω0=k/m,2β=c/m,h=F0/m,则式(1)可写成式(2)。
式中:
c——粘滞阻尼系数;
k——结构的弹性系数;
x,β,h——无量纲系数。
这就是受迫振动的微分方程。注意到ω0是振子系统无阻尼振动的固有频率,当系统受到角频率为ω的策动力时,系统最后稳定状态的频率将是ω,而不是ω0,显然受迫振动系统响应发生在策动频率上,可以肯定,当结构自振频率较低(即柔性结构)时,强风对结构容易产生时程共振,其位移响应中的脉动分量更加突出,也可通过实验得以证实。
2.1 实验目的
定向分析讨论塔机摇摆振动幅度在持续风载和受迫共振风载2种情况下的响应。
2.2 实验可行性分析
单摆振子采用小钢球作为受风物体,灵敏度高,能反映本实验的真实情况。回复力T'=-Gsinθ,而理想弹簧振子的回复力F=-kx,就振子回复力大小而言,当θ→0时,可认为T'=F。
2.3 实验过程
事实上,找一个理想的振动装置,将它完全放入一个风洞实验装置中,并模拟台风风速v=30~70 m/s的大功率供风是不容易的。因此采用以下方法进行情景模拟:
如图3所示,把一个简易的单摆摆球装置放置于简单的风洞中,持续施加稳定风速于摆球上,摆球受风力作用偏离垂直位置摆到一个稳定位置(记为1位置)。解除风场,摆球得到了一定的势能,必将以垂直线为中心线摆动,不计短时间内的能量损失,摆球将继续做同振幅振动。根据观察,模拟塔机遭受台风过程中的危险情形:当摆球从最左端向原风场同向摆动,T/4时刻后经过最低点时施加一个同向且同大小的风场(即恢复原风场),当摆球摆到右端最高位置时,得到单摆在共振风场作用下的最大振幅(记为2位置)。再次让单摆做预定位置(1位置)小幅度振动,当摆球处于最左端(对称1位置)开始与风向同方向运动时(记为T时刻)恢复原风场作用,得到一个单摆在风场中的最大振幅(记为3位置)。这样,利用轨迹最高点的位置就能反映单摆振子受静风载荷作用和规律脉动风荷载作用下2种情形的差别。本实验仅定性讨论持续风载和受迫共振风对摇摆振动物体运动幅度的影响,略去风力系数、挡风折减系数等要素。

图3 风洞实验布置
风洞实验图见图4,由吹风筒、有机玻璃管、悬挂小钢球及便携式风速测试仪等组成一个简单的测试验证装置。小钢球直径d=2 cm,单摆有效长L=75 cm;测得风筒出风口处风速V0=8.5 m/s。采集数据点见图5,结果记录见表1。

表1 单摆实验数据记录mm

图4 风洞实验
图5 实验数据点记录
2.4 实验真实性验证
实验铁质小球直径d=2 cm,小球挡风面积s=πd2/4=3.14×0.022/4 m2=3.14×10-4m2,小球重力G=mg=ρvg=7.8×103×4πr3/3×10 N=0.33 N。根据GB/T 3811—2008中风速与风压的关系式P=0.625vs2,得vs=8.5 m/s时,P=0.625×8.52N/m2=45 N/m2,小球受到的水平风力T=P×s=45×3.14×0.012N=1.41×10-2N;从力学分解可知,摆动角度θ=arcsin(T′/G)=arcsin(1.41×10-2/0.33)=0.042(θ≤5°时,T与T′可等同使用),得线段AB=L×tanθ=2.9 mm,实际测量均值为2.7 mm,误差Δ=(2.9-2.7)/2.9×100%=6.9%,结果可信。对线段AC、AD利用同样方法算出其他对应量见表2。
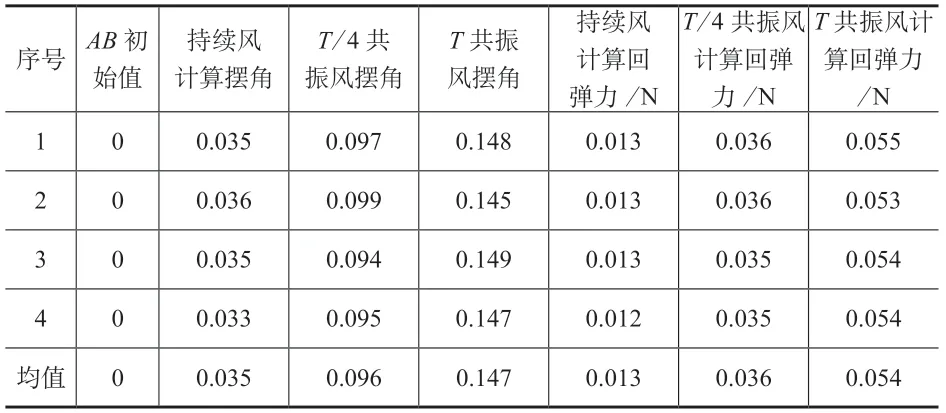
表2 单摆实验数据统计
2.5 实验数据讨论
根据图3,在摆锤夹角θ很小的情况下,单摆振子的回复力等于理想弹簧振子的回复力。分析表2数据,T/4共振风作用下小钢球获得的回弹力FT/4与持续风作用下小钢球获得的回弹力F0的关系为FT/4/F0=0.036/0.013=2.77倍,T共振风作用下小钢球获得的回弹力FT与持续风作用下小钢球获得的回弹力F0的关系为FT/F0=0.054/0.013=4.15倍。
根据实验结果,绘出风振位移-时程关系图,如图6所示。可以肯定,当结构自振周期越长(即柔性结构),脉动风对结构越容易产生共振,其位移响应中的脉动分量更加突出。如果在回荡到达左停止点后继续模仿共振风施加同样风场,钢球将继续吸收风动能,振幅将到达新的高点。这种反复与单摆同步风场,振子的振幅响应明显加大。根据《结构风工程》[8]中引用的高斯分布(Gauss)理论,这种情况发生的概率越来越小。

图6 风振位移-时程关系
2.6 实验数据误差分析
实验结果测得平均值:AB=2.6 cm,BC=4.7 cm,CD=2.7 cm;其中B点为初始摆角θ=arctan(2.6/75)=0.033,与理论计算结果有一定差距。原因有:1)测量数据存在测量误差;2)实验受器材限制,玻璃管开口存在风程损失,影响实验结果;3)堵塞效应影响真实风场作用结果;4)共振风作用时间是人为模拟,风场建立和撤除时间存在误差;5)其他误差和影响,如测量仪器、钢球固定绳索等造成的误差难以避免。
本次讨论的是模拟台风过程中风场作用时间与塔机摇摆受迫共振的响应,是定向讨论,而非定量分析。因此,通过实验能够明显体现台风风场与塔机摇摆同步时对塔机结构响应带来的影响。以上定量分析结果虽然存在误差,但不影响结论。
2.7 实验拓展
塔机平衡臂和工作臂横架在塔身标准节顶部回转装置之上,在风力作用下,虽然随风旋转到顺着风力的方向,减小了受风面积。但在其非顺风方向上,长长的平衡臂和吊臂也同时受到风场漩涡横风作用。一般而言,塔机附着在高层建筑上,建筑物可以看作相对静止,塔机由于自身属于桁架结构,在跨临界风场中产生的周期性脱落并不明显,但建筑物在跨临界风场中产生的周期性横风脱落会直接影响塔机平衡臂和工作臂。这种叠加响应与塔机工作臂和楼面间的距离以及夹角有一定关系。如图7所示,风场从左向右在建筑物正面形成正压区,在建筑物的背面形成负压区。风来流轨迹质点A、B、C、D受建筑物钝体阻挡向上扬起,上扬角度随风速的变化而变化。流经建筑物上方后在建筑物背面负压区随着建筑物造成的漩涡脱落,改为下沉方向。此时在塔机后方平衡臂(1区)会出现一个上扬风场,而同时前方工作臂(2区)则产生一个下沉风场。从风场质点作用效果看,风场的某一个质点(如C质点)先对平衡臂“上抬”,经过一段时间Δt后又对工作臂进行了“下按”,或者说某一质点在“上抬”平衡臂的同时,在Δt时间前的另一个质点同时在“下按”工作臂。这就在塔机这段结构上除了水平顺风推力外还对塔身产生力偶矩,即进一步增加塔机这段结构获得摇摆振动的动能。这种周期明显与塔机振动周期一致的风场确实存在,通过多次实地对台风中塔机的摇摆振动进行观察,发现台风风场极不稳定,在每次台风开始到结束,总会存在这种短时间内巧合的节奏风场,如阵风场或旋转风场等;塔机通常挨着楼边,风场在高楼的阻挡后,确实在其背风处形成多个漩涡脱落,特别是塔机上机体离楼面较近时对塔机的工作臂和平衡臂作用非常明显。图8中风场受到建筑物群的阻挡,同时形成多个不同向的风场,导致相隔不远的2台塔机出现不同的摆向(图中A、B所指向),同时塔身发生明显的弯曲摇摆。

图7 附着塔式起重机的台风风场

图8 漩涡脱落对塔机工作臂的偏摆
参考GB 50009—2012《建筑结构荷载规范》中附录F.1.1[9],一般高耸钢结构基本自振周期T=0.013H。以某公司普通QTZ63型塔机为例,离地面独立高度设计值为40 m,高层安装附着装置时自由高度为35.5 m,综合塔机上机体,结构计算高度按H=40 m计算,基本自振周期T=0.013×40 s=0.52 s。当然,每个型号规格塔机基本自振周期应根据生产单位生产的塔机所选取的型材和制造工艺不同而不同,自振周期与结构的质量和刚度有关,可以通过改变截面或结构形式等手段来达到改变的目的。现场安装高度也是决定因素之一,例如塔机随着安装高度的不同,塔身刚度不同,其基本自振周期也不同。但塔机回转装置以上部分,从十几吨到几十吨甚至更大的振动质量,工作臂加上平衡臂长度从几十米到近百米的大尺寸振动响应尺寸,横架于塔身顶部。严重的质量突变、偏移以及平衡臂加工作臂的横风效应对整机自振周期的影响程度是很明显的,应当做进一步探讨。一次台风过程风力从小到大,其湍流输送的一系列大小不同的漩涡所引起的风场随时间变幻不定,其风振强度、周期也非常容易与塔机自振周期相近甚至一致,因此塔机结构发生强迫共振的概率并不低,将产生比稳定风作用大几倍甚至几十倍的共振响应,破坏极为严重,应当引起重视。在我国沿海台风高发地区,针对风载较敏感的起重机械,GB 50009—2012中8.4.1条要求,当其自振周期T≥0.25 s时(上述计算结果T=0.52 s符合),应考虑风压脉动对结构产生顺风向风振的影响,顺风向风振响应按结构的随机振动理论进行计算。GB 50135—2019《高耸结构设计标准》中4.2.9条关于考虑风压脉动和风压高度变化的影响系数计算中[10],对于结构外形或质量有较大突变的高耸结构,风振计算均应按随机振动理论进行。
3 结束语
综上所述,虽然上述实验过程较为简单,所建立的风场与实际台风风场有相当大的差异,但其结果基本能直观反映塔机在强台风风振中的存在情况。塔机这种既有结构外形突变又有质量较大突变的高耸结构,更应该对其非工作状态下的风荷载做进一步探讨。从外形受横向风影响大、质量突变大、易发生强迫共振等方向适当增强其抗风能力验算,尽可能地提高我国沿海台风高发地区塔机的本质安全。

