基于BP 神经网络的高分辨率海底地形跨层生成模型

王振，张锡亭，王建华

1. 北京航空航天大学 数学科学学院，北京 102206

2. 大连理工大学 工业装备与结构分析国家重点实验室，辽宁 大连 116024

3. 大连理工大学 数学科学学院，辽宁 大连 116024

4. 长沙矿冶研究院有限责任公司，湖南 长沙 410006

地球上海洋总面积约为3.6 亿平方千米，占地球表面积的71%，蕴含巨大资源[1]。海底地形作为海洋研究的基础地理信息，对海洋资源开采、水下设备研发以及对海底构造运动和海洋环流的研究具有重要意义[2]。但由于海底环境的特殊性以及采样困难问题，造成海底地形数据网格精度不足，这给海洋事业发展带来挑战。海底地形复杂多变，高分辨率的水下地形的生成对于船舶、水下航行器等海洋工程装备的路径规划和安全行驶十分重要。

提高海底地形图像的分辨率面临诸多困难，如何通过对有限测量数据的有效填充生成高分辨率地形是急需解决的问题。国内外研究人员提出很多种数据插值算法。如最近邻域插值和线性插值，但由于最近邻域插值在运算时直接选用邻近的数据进行插值计算，得到的图像的边缘容易是锯齿状的，视觉效果较差。而线性插值数据量小、速度快，相对于最近邻域插值方法来讲，插值效果较好，但是其插值过程中会丧失一些高频成分，使得图像处理后变得有些模糊。为了改善上述情况，基于高阶多项式的多项式内插算法被应用于图像处理中，如Keys[3]提出立方卷积插值和Hou 等[4]提出三次样条插值改变了图像边缘锯齿状以及图像模糊的问题，但是计算复杂、计算量大。于是，Reed 等[5]提出了基于最小二乘法和线性插值方法的线性样条插值方法以及Truong 等[6]提出基于最小二乘法与立方卷积插值函数的立方卷积样条插值算法，经验证比起先前的插值算法，会获得更清晰的图像，但是其计算复杂度相对较大 , 特别是算法中的计算循环卷积部分。除上述插值方法外，比如Schafer 等[7]提出基于贝叶斯方法和最大似然的插值算法，Li 等[8]提出基于模糊聚类的插值算法，这些数据插值算法在填充数据量小的问题上取得显著的效果，然而面对大规模数据填充任务时，精度急剧下降，这是由于大规模数据存在着丰富的数据信息维度，而这些数据插值算法不能有效体现大规模数据的深度特征[9]。在地形数据处理方面，南非矿产地理学家Krige 提出了克里金插值算法。克里金插值算法相比于传统线性插值算法具有更高的精度，在地质统计学及图像处理等方面获得了广泛应用[10]，但它本质上是一种光滑的内插值算法，生成图像较光滑，然而真实的地表具有复杂性，用这种插值算法建立的模型未能体现真实地表最重要的特征[11]。

为了更好地提高图像的质量，近几年许多新方法被提出，比如Ramponi 等[12]提出空间可变的插值算法, 该方法利用相邻点之间的不对称性引入加偏差的距离，从而有效保护了图像的局部特征，进而提高重构图像的品质。Thurnhofer 等[13]提出自适应插值算法，根据原始图像的不同区域的不同的结构特性，采用的不同的插值方法。为了更好完成大规模数据填充任务，大热的机器学习方法被用于数据插值中，如Narang 等[14]提出K近邻插值算法；Wang 等[15]提出基于支持向量回归方法的数据插值方法；Shi 等[16]提出PixelShuffle 算法；Tian 等[17]提出DUpsampling 算法；张守建等[18]提出基于多层前馈神经网络（back propagation,BP）的数据填充方法，应用于我国西南地区地形数据中。伴随着海底开发工程装备的发展，对海底高分辨率地形的需求变得十分迫切，但现有方法大多是基于邻点的经典数据填充格式，很难反应海底地形的地貌特征，而利用有限采样数据获得相邻样本间的内在联系，同时保持整体特征的地形生成方法值得深入研究探索。

本文在有限采样数据下，通过BP 神经网络建立具有跨层生成网格样本能力的海底地形生成模型，对海底地形样本填充，形成高分辨率海底地形图像。

1 高分辨率海底地形跨层生成模型

在保持样本数据整体特征的前提下生成满足高分辨率要求的海底地形，本文建立具有跨层网格生成效果的BP 神经网络模型对原始网格型海底样本加密填充，从而获得高分辨率海底地形图像。

1.1 模型建立

本文针对如图1 所示的规则网格地形样本进行加密填充。图1 中黑色圆形实心点代表测量地形已有样本网格点，记为第1 层网格；绿色菱形实心点代表目标生成的网格点，记为第0 层网格。将第1 层网格每隔一行采样一行，每隔一列采样一列，得到的更稀疏的网格样本记为第2 层网格，同理可生成更稀疏的高层网格。在第k层网格中取(m×n)个网格点组成第k层网格的网格单元，第一层网格的(3×3)网格单元如图1 中红框所示。在每个第k层网格单元中，相邻的上下左右4 个等间隔网格点构成的小单元的中间位置为其对应的第k−1层网格。

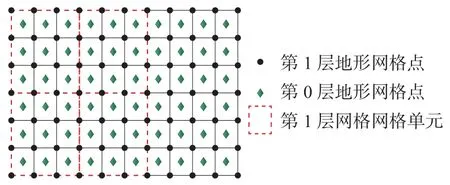
图1 海底地形样本网格点示意

由于空间自相关性，同一区域地形数据具有相同的统计特征和随机性[18]，因此通过大量网格单元样本训练，神经网络模型已将区域海底地形地貌数据随机特征和统计特征融入跨层网格样本间非线性映射关系中。采用这种方法得到的跨层网格生成模型既能表达网格点之间的相邻关系，也能表达区域地形的随机统计特征。利用3 层BP 神经网络[19−25]构建高分辨率海底地形跨层生成模型，将第k层网格地形样本和第k−1层网格地形样本作为训练集，通过BP 神经网络获得两者间的非线性映射关系，形成具有跨层网格生成能力的BP 神经网络模型。

式中：W(1)、W(2)分别为输入层到隐藏层以及隐藏层到输出层权重矩阵；分别为输入层到隐藏层和隐藏层到输出层的阈值矩阵；Z(1)为输入层的输出值构成的矩阵；A(2)为隐藏层的输出值构成的矩阵；f为激活函数，用于隐藏层的传递，以达到增强BP 神经网络模型非线性逼近能力的目的。

假设模型训练样本为第k层原始海底地形网格样本Xk及其对应的第k−1层原始海底地形网格样本Xk−1，样本Xk以输入层–隐藏层–输出层的方向[26]，按照式(1)～式(3)运算，得到经BP 神经网络正向传播运算后的第k−1层海底地形网格样本Ok−1。

考虑到正向传播结束后样本Ok−1与样本Xk−1之间有误差，根据两者的均方误差利用梯度下降法，沿输出层–隐藏层–输入层的方向，进行误差反向传播[27]，从而得到更新后的层间连接权重矩阵和阈值矩阵。

经过正向传播和反向传播之间的反复迭代，直到误差达到容许的范围或者循环达到设定的次数，则训练过程完毕。BP 神经网络会保存一套层间连接权重矩阵和阈值矩阵，形成如式(4)所示的用于反映训练集中样本Xk与样本Xk−1之间非线性映射关系的跨层网格生成模型。

为检验跨层网格生成模型Fk→k−1对第p层海底地形网格样本Xp的适用性，将Fk→k−1应用于Xp。

按照式(5)，生成第p−1层海底地形网格样本Xp−1，完成对样本Xp的加密填充。以上过程记为Fk→k−1,p→p−1。

通过已有样本数据检验模型Fk→k−1对第p−1层数据的生成质量，确定上述训练模型的适用性，也部分说明跨层网格样本之间具有相似的数据结构。因此可以利用训练好的模型F2→1应用于第1 层网格样本，也是给定的最精细网格，生成更精细的第0 层网格样本，即X0=F2→1(X1)，得到最终加密填充后的样本数据。

1.2 模型检验

为验证模型是否可以在不改变样本统计特征的前提下，完成对海底地形样本的加密填充并提高海底地形图像的清晰度，本文使用Mann-Whitney U 检验、Levene 检验和图像清晰度3 个指标进行比较、验证。

1.2.1 Mann-Whitney U 检验

Mann-Whitney U 检验[28−29]假设原始海底地形样本Xk−1和模型生成的海底地形样本Ok−1分别来自除了均值以外完全相同的2 个总体，由此检验2 组样本的均值是否有显著的差别。令WXk−1Ok−1表示Xk−1样本观察值小于Ok−1样本观察值的个数，m和n分别表示Xk−1和Ok−1的样本个数，则检验统计量Z为

检验统计量Z服从标准正态分布，当求得的P值大于显著性水平0.05 时，认为2 组地形样本均值相等。

1.2.2 Levene 检验

Levene 检验[30−31]是一种方差齐性检验的方法。利用该检验方法来检验原始海底地形样本Xk−1和模型生成的海底地形样本Ok−1的方差是否相同。令Z1.和Z2.分别为Xk−1和Ok−1经转化后的数值，和分别为转化后2 组地形样本的均值，表示Z1.和Z2.全部为地形样本的均值。转化公式及检验统计量W为

检验统计量W服从F(1,m+n−2)分布，当求得的P值大于显著性水平0.05 时，认为2 组地形样本之间方差相等。

1.2.3 图像清晰度

本文采用基于频率域特征的评价函数[32]来计算像素矩阵为M×N型矩阵的海底地形云图的图像清晰度，计算过程为：

1）将海底地形云图RGB 图像转化为对应的灰度图像，利用加权平均法计算图像每一点的灰度值。

式中：(x,y)为图像矩阵中每一点的坐标；R、G、B为三元光色红、绿、蓝强度值，任何一种颜色都可以由这3 种颜色表示，R、G、B取值范围都为0 ～255。

2）对转变为灰度值后的海底地形云图图像数值矩阵进行二维离散傅里叶变换，转换到频域。

3）计算海底地形云图图像清晰度数值。

式中：R(µ,ν)和I(µ,ν)分别为傅里叶变换F(µ,ν)的实部和虚部；G为图像的清晰度数值，该数值越高，图像越清晰。

2 南海海底地形生成与分析

利用Python 搭建海底地形跨层生成模型，完成对原始网格型海底地形样本加密填充。为了确保模型有效，选取南海海底网格型样本作为算例进行训练分析。采用ETOPO5 (https://www.ngdc.noaa.gov/mgg/global/relief/ETOPO5/TOPO/ETOPO5/)中南海海域网格型海底地形数据作为样本进行训练，具体为东经105.004 2°～124.995 8°, 北纬21.362 5°～24.995 8°。选取3 种跨层取样方式：将整体网格型原始海底网格样本按照紧密相连的(3×3)个、(6×6)个、(12×12)个网格形成的网格单元进行分割。在3 种网格单元中分别以1 个、2 个、4 个网格上下左右等间隔取样，每个网格单元都分别含有16 个第1、2、3 层样本取样位置，9 个相对应的第0、1、2 层样本取样位置。取样位置举例说明如图2 所示。

图2 取样位置图像

将跨层取样后的海底地形样本划分3 种不同的训练集和测试集的组合验证模型效果。它们分别为：1）将171 570 组第2 层样本和其对应的第1层样本随机分为170 570 组训练集和1 000 组测试集。利用模型获得训练集中第2 层样本与第1 层样本之间的映射关系F2→1，将其作用于测试集的第2 层样本中，生成相应的新第1 层样本，与这种样本组合相关的模型运行过程用F2→1,2→1标记。2）将83 580 组第3 层样本和其对应的第2 层样本随机分为82 580 组训练集和1 000 组测试集。通过模型将训练集中的第3 层样本与第2 层样本之间的映射关系F3→2作用于测试集的第3 层样本中，生成相应的新第2 层样本，与这种样本组合相关的模型运行过程用F3→2,3→2标记。3）将83 580 组第3 层样本和其对应的第2 层样本作为训练集，随机选取1 000 组第2 层样本及其对应的第1 层样本作为测试集。通过模型将训练集中的第3 层样本与第2 层样本之间的映射关系F3→2作用于测试集的第2 层样本中，生成相应的新第1 层样本，与这种样本组合相关的模型运行过程用F3→2,2→1标记。在算例运行过程中，为使各变量处于同等重要位置，保证模型运行结果的可靠性，对样本标准化后再进入模型训练。

2.1 海底地形跨层生成

本文BP 神经网络的输入层、隐藏层和输出层的神经元个数，分别为16、40 和9，学习率为0.000 1，一次训练选取的训练样本组数为7，所有训练样本最大训练轮次为400，选取的激活函数为tanh 激活函数，根据激活函数，本文使用的权重矩阵初始化方法为Xavier 初始化[33−34]。F2→1,2→1、F3→2,3→2、 F3→2,2→1共3 种组合模型运行结果如图3～8 所示。

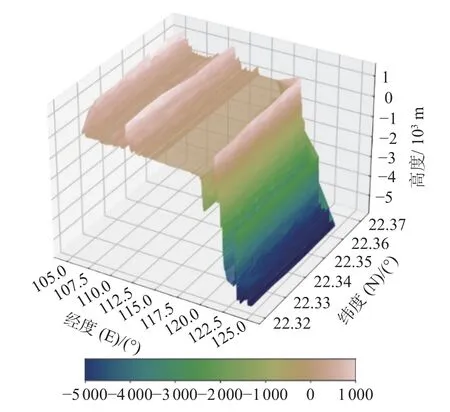
图3 F2→1,2→1 第 1 层原始海底地形样本构成的三维图像

图3 、图5 和图7 表示3 种不同组合方式下测试集中原始海底地形样本构成的三维图像；图4、图6 和图8 表示3 种不同组合方式下由模型生成的海底地形样本构成的三维图像。由同种组合方式的2 个图像对比可知，模型生成的海底地形样本与原始海底地形样本相差不大。为更客观地评价海底地形跨层生成模型结果，本文不仅对三维海底地形图像进行对比，并且进行理论分析。如表1 所示，将3 种不同组合的模型运行结果与克里金插值算法对比，以均方误差、相对误差、决定系数、Mann-Whitney U检验和Levene 检验为对比指标进行比较。

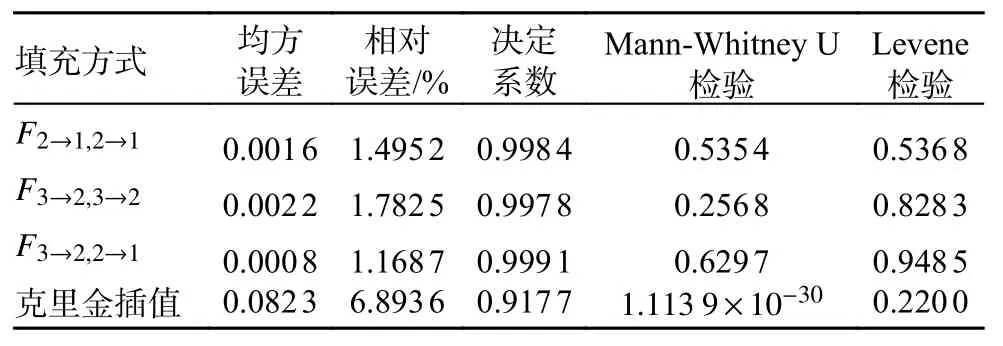
表1 不同填充方式的误差及假设检验结果对比

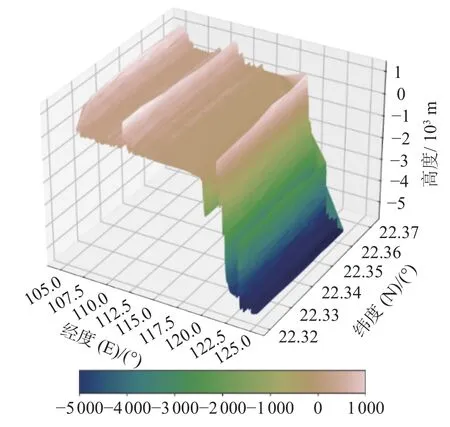
图4 F2→1,2→1模型产生的第 1 层海底地形样本构成的三维图像

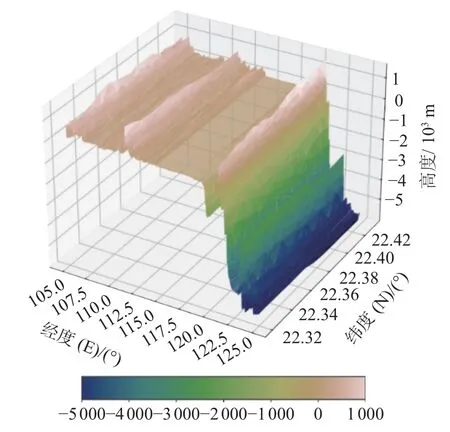
图5 F3→2,3→2第 2 层原始海底地形样本构成的三维图像

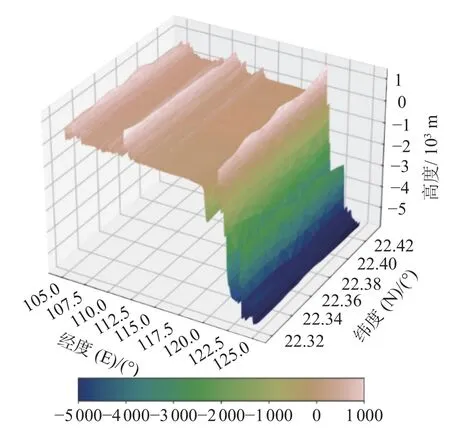
图6 F3→2,3→2模型产生的第 2 层海底地形样本构成的三维图像

图7 F3→2,2→1第 1 层原始海底地形样本构成的三维图像

根据表1 可知，由F2→1,2→1、F3→2,3→2和F3→2,2→1这3 种组合方式对应的高分辨率海底地形跨层生成模型产生的海底地形样本与原始海底地形样本之间均值和方差相同的假设都成立，而由第2 层原始海底地形样本和克里金插值方法共同产生的第1 层海底地形样本与第1 层原始海底地形样本之间不能通过均值相等的检验。对于模型生成的海底地形样本与原始海底地形样本之间的均方误差和相对误差，模型低于克里金插值。在决定系数方面，模型高于克里金插值。因此，该模型可以在不改变数据统计特征的前提下，利用跨层网格生成策略完成对海底地形数据的填充。

2.2 有效性验证

由上文可知，本文建立的海底地形跨层生成模型可以有效获取跨层样本间的非线性映射关系，并运用到其他层网格样本生成中。为完成原始网格型海底样本的加密填充，本文参照F3→2,2→1运行模式，利用F2→1,1→0运行模式，获得第0层海底地形样本，完成对原始海底地形样本的加密填充。为体现高分辨率海底地形生成模型对样本的填充效果，随机选取该海底2 个局部地区，得到2 个地区的样本填充前后的三维海底地形对比图像，如图9 ～ 18 所示。同时，利用Mann-Whitney U 检验和Levene 检验来检验2 个地区样本填充前后的统计特征的一致性，并由克里金插值对相同区域的第1 层原始海底地形网格样本加密填充，以图像清晰度为依据比较两者生成的海底地形云图图像的质量，具体结果如表2 和表3所示。

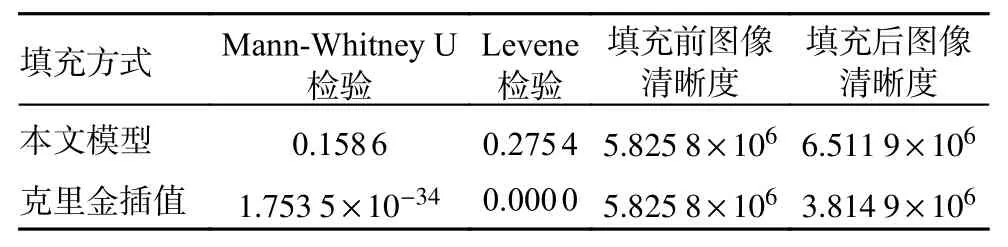
表2 本文模型生成地形和克里金插值结果的数据的有效性对比(局部地区1)

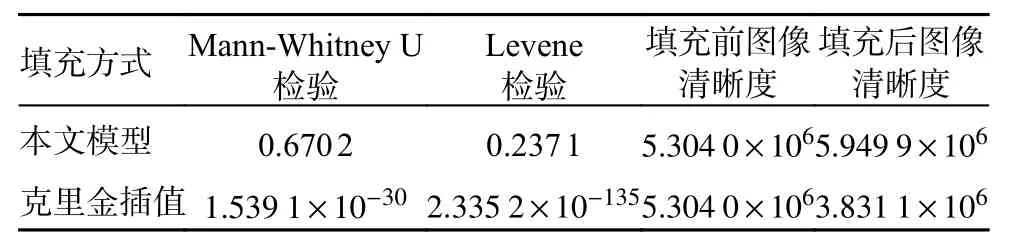
表3 本文模型生成地形与克里金插值的数据的有效性结果对比(局部地区2)

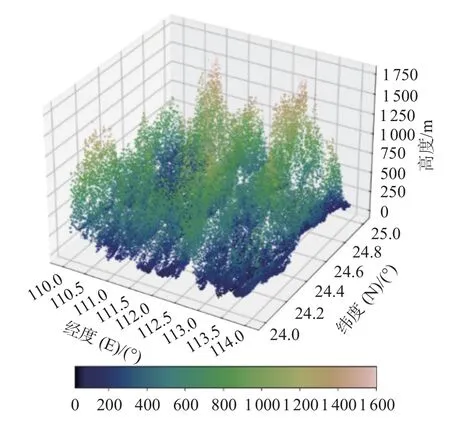
图9 局部地区1 原始样本海底地形三维图像

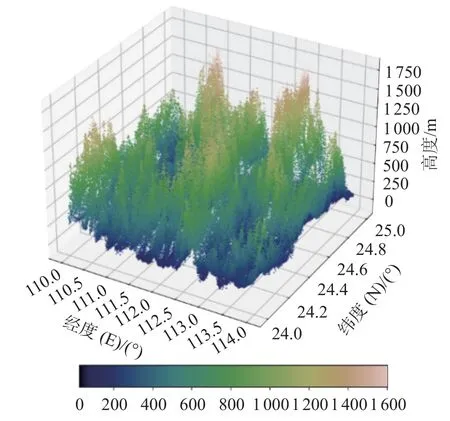
图10 局部地区1 模型填充后海底地形三维图像

由图9～10 对比以及图14～15 对比可知，本文高分辨率海底地形跨层生成模型可以对地形数据进行合理的填充，并且由图11～13 对比以及图16～18 对比可知，克里金插值方法获得的图像过于光滑，没有体现出海底的地形特征，而本文模型生成的图像在提升清晰度的同时，保证了生成的海底地形图像有效性。由表2 和表3 可知，本文构建的高分辨率海底地形跨层生成模型对样本填充效果良好。Mann-Whitney U 检验和 Levene检验结果显示，填充前后样本的均值和方差没有显著差异。通过图像清晰度计算结果可知，该模型对样本填充后图像的清晰度高于原始样本图像以及克里金插值填充后样本图像的清晰度。

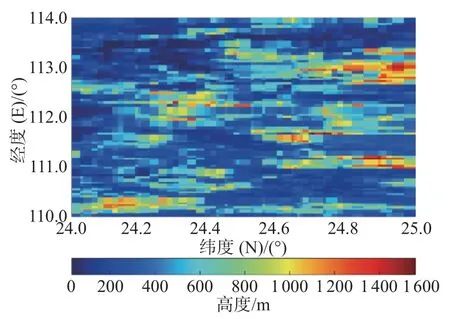
图11 局部地区1 模型原始样本海底地形云图

图12 局部地区1 模型填充样本后海底地形云图

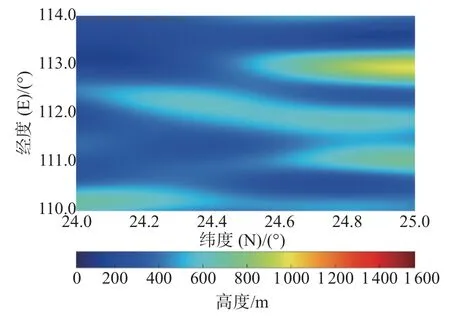
图13 局部地区1 克里金插值后海底地形云图

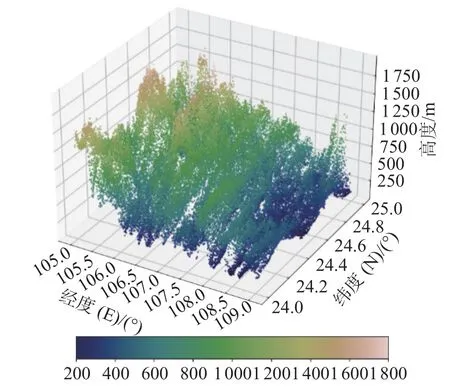
图14 局部地区2 原始样本海底地形三维图像

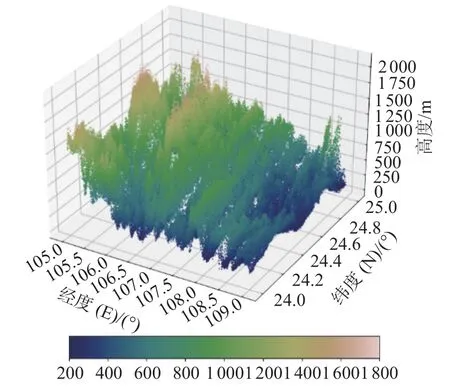
图15 局部地区2 模型填充后海底地形三维图像

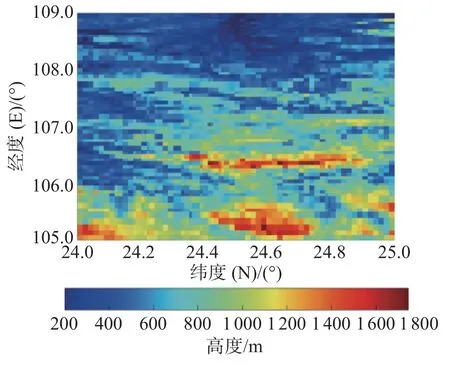
图16 局部地区2 原始样本海底地形云图

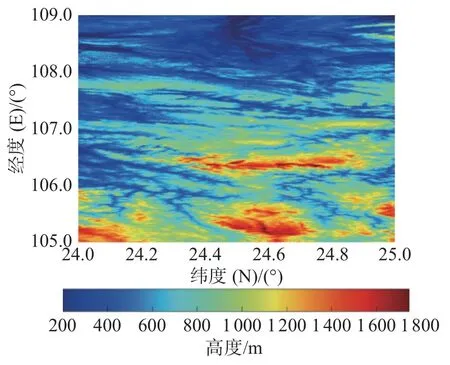
图17 局部地区2 模型填充样本后海底地形云图

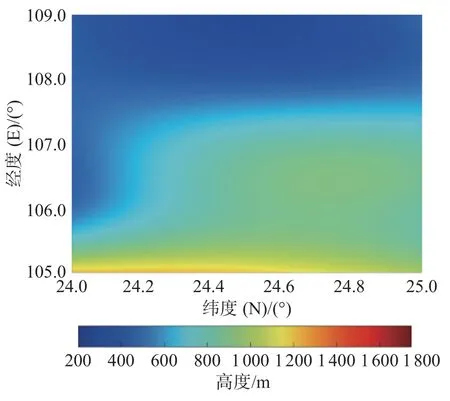
图18 局部地区2 克里金插值后海底地形云图

3 结论

本文基于BP 神经网络建立了具有跨层网格生成能力的高分辨率海底地形跨层生成模型，通过南海海底地形验证了该模型产生的数据兼顾了原始样本的相邻数据关系和整体数据特征。

1）模型利用BP 神经网络的泛化能力，将高层网格样本与其对应的低层网格样本之间的非线性映射关系迁移至其他层网格样本生成中，并根据均方误差与相对误差验证了该模型具有有效的网格样本跨层生成能力。

2）通过假设检验，验证了该模型生成样本可以表征出原始样本的统计特征。

3）由云图图像及其清晰度的计算结果表明，相较于传统克里金插值方法，该模型的结果良好。因此，本文模型可以有效获取并迁移跨层网格间的相关关系至其他层网格数据生成中，完成对海底样本的加密填充，生成高分辨率图像用于展现海底地形。机器学习和跨层网格生成方法的结合方式给海底地形的研究提供了一种新的思路，高分辨率海底地形跨层生成模型在更大地形范围以及更多海山、海脊等海底地貌特征方面具有广阔的应用前景。