波形腹板钢-混组合箱梁畸变效应分析*

岳 阳 杨黎明 康 健 李 峰

(1.甘肃五环公路工程有限公司 兰州 730050; 2.甘肃省桥梁工程研究中心 兰州 730050)

波形腹板钢-混组合箱梁结构将混凝土和钢材的材料特性有效地组合起来,使得2种材料得到了充分利用,但是在偏心荷载作用下也更易产生畸变变形。

近年来,我国学者对箱型截面的畸变效应进行了充分研究。李宏江等[1]在弹性地基梁法的基础上对波形腹板钢-混组合箱梁畸变进行实验研究,并对波形钢腹板预应力混凝土组合箱梁扭转与畸变研究进展进行了阐述[2]。刘保东等[3]对内衬混凝土对波形钢腹板刚构桥扭转和畸变性能的影响进行了研究。马磊等[4]对单箱双室波形腹板钢-混组合箱梁进行了有限元分析和试验研究;张元海等[5]对箱形梁畸变效应受跨中横隔板的影响规律进行了研究分析。尽管研究人员对箱梁畸变效应的研究已较为全面,但是鲜有人将畸变分析理论与传统扭转分析理论相统一。

为了优化组合箱梁设计理论和施工方法,本文利用与传统混凝土箱梁扭转效应分析理论相统一的畸变效应分析思路,重新定义畸变角,推导建立畸变微分方程,并根据波形腹板钢-混组合箱梁的畸变翘曲应力随混凝土厚度差的变化规律,对设计施工提出建议。

1 畸变角

根据截面等效原理将组合截面等效为混凝土截面[6-9],建立以O点为形心坐标原点x、y轴为形心主轴的坐标系,设畸变中心位于D点,顶板至形心的距离为y0,畸变中心至形心距离为yD,b1、b2分别为顶底板宽度的1/2,b3为翼缘板的宽度,bw为腹板的截面长度,h为箱梁高度,α为腹板的俯角,t1、t2分别为箱梁顶、底板的厚度,箱梁截面计算简图见图1。

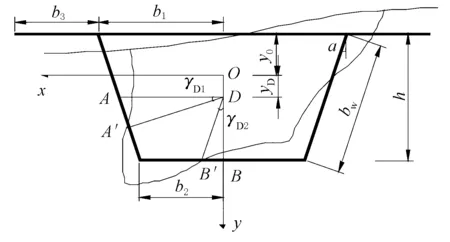
图1 波形腹板钢-混组合箱梁畸变简图

用水平线段穿过交于A,竖直线段穿过D点交于B,当箱梁产生畸变变形时,A和B就会移动到A′、B′的位置。定义∠ADB的改变量为畸变角,用γD表示,γD由两部分组成,即

γD=γD1+γD2

(1)

在规定畸变角的方向时,以∠ADB减小为正,虽然传统畸变分析方法与扭转分析方法具有差异性,但按照本文定义的畸变角进行畸变分析使得两者更具统一性。

2 畸变总势能

2.1 畸变翘曲应变能

箱梁截面模型分别发生畸变角γD1和γD2时各板件的变位图[10]见图2。

图2 变位图

以周线坐标s逆时针方向为正,则顶底板及腹板切向位移可表示为

(2)

式中:x1为A点到y轴的距离。

畸变时纵向翘曲位移w满足闭口截面变形连续条件,若对式∂ut/∂z+∂w/∂s=0积分一周,即

(3)

将式(2)代入式(3)为

γD2′=kDγD1′

(4)

式中:kD=x1h/[b1(y0+yD)+b2(h-y0-yD)]。

对式(4)两边进行积分可得γD2=kDγD1+C,因为畸变角γD1、γD2彼此不独立所以积分常数C=0,为方便计算可将γD1和γD2用来表示,即

(5)

将式(5)代入式(2),可得畸变翘曲位移对周线坐标s的一阶偏导数为

(6)

将式(6)两边对s积分,可得

(7)

式中:w0为畸变翘曲位移在周线坐标初始点处的值,当s的起始点位于y轴和周线的相交处w0=0时 ,此时畸变翘曲位移w的表达式为

(8)

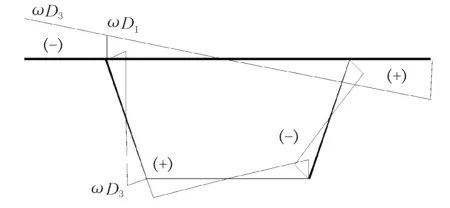
图3 畸变扇形坐标

通过计算可知,翼缘端部、腹顶板相交处、腹底板相交处的畸变扇性坐标可表示为

(9)

由胡克定律求得各点的畸变翘曲正应力σD,即

(10)

腹顶板相交处翘曲应力σ1和腹底板相交处翘曲应力σ2之比β的表达式为

(11)

整理后,可得畸变中心竖坐标

(12)

箱梁截面在产生畸变变形时,其截面上的翘曲应力满足在自身平面内平衡的条件,即

(13)

根据式(13)中第2项的平衡条件可得畸变应力之比β

(14)

根据式(10)可得翘曲应变能U1

(15)

式中:v为箱梁结构的体积;L为箱梁结构的跨长;IωD为畸变翘曲惯性矩。

2.2 横向框架应变能

以单位梁段进行分析,其横向框架变形图见图4。用u、v、θ表示任意一点沿x、y轴方向的位移和转角。

图4 横向框架变形图

(16)

用ui、vi(i=1,2.3,4)表示4个角点的位移,则1、2角点的位移ui与位移vi为

(17)

其中

(18)

其角点1和角点2点处的弯矩表达式为

(19)

式中:Es为钢材的弹性模量;Ec为混凝土弹性模量。

将式(17)代入式(19),再根据角点1处的弯矩平衡条件,可以得出m1(1-4)+m1(1-2)=0,即

(3io+4iw)θi+2iwθ2=-(3io/b1)Dv1γD+ξ

(20)

其中

角点2处的弯矩平衡表达式为

(21)

波形腹板形状见图5。

图5 波形钢腹板形状图

根据移轴及转轴公式以单个波段的腹板进行计算有

(22)

式中:tw为钢腹板厚度;L为波形钢腹板的周期长度。

联立式(20)、式(21)和式(19)则可以计算得出角点1与角点2处的弯矩值。其弯矩为

(23)

其中

且

以结构的对称性和弯矩分布的反对称性,可求得整个框架上的弯矩,从而得出畸变横向框架应变能U2,即

(24)

2.3 畸变荷载势能

分布及端点节点力作用下外荷载所做的功为

(25)

其中:FT为作用在边界横截面上的畸变广义力向量;u为畸变广义位移向量。具体为

(26)

将式(18)和式(26)代入式(25)便可得到产生畸变角γD时所对应的的畸变荷载md的表达式,计算过程如下。

(27)

由式(27)可以得出,md的表达式为

(28)

式中:md为分布畸变荷载;PD为作用在1、4角点处的反对称荷载。

2.4 畸变总势能

以翘曲应变能、横向框架应变能、外荷载势能三者之和可得畸变总势能∏的表达式为

(29)

3 畸变控制微分方程及其初参数解

依据势能驻值原理,对式(29)进行一阶变分运算,则有

(30)

按照驻值原理,δ∏=0,可得控制微分方程为

EIωDγD″″+EIRγD-md=0

(31)

即

γD″″+4λ4γD=md/(EIωD)

(32)

由式(30)中的边界项可得,畸变矩MD和畸变双力矩BD,即

(33)

式(32)所对应的微分方程的通解为

γD(z)=A1sh(λz)cos(λz)+A2ch(λz)cos(λz)+A3ch(λz)sin(λz)+A4sh(λz)sin(λz)

(34)

4个初参数γD0、γD0′、BD0、MD0分别为箱梁在z=0处的畸变位移、畸变广义翘曲位移、畸变双力矩和畸变矩。根据式(33)和(34),可得畸变方程的初参数解。

[sin(λz) ch(λz)+cos(λz)sh(λz)]+

[cos(λz)sh(λz)-sin(λz)ch(λz)]

(36)

根据结构约束情况,确定初参数γD0、γD0′、B0、M0后,进而得出扭转角和翘曲位移的值。

1) 简支端:

γD=0、γD″=0

2) 固定端:

γD=0、γD′=0

3) 自由端:

γD″=0、γD‴=0

4 算例分析

以桑园子黄河大桥40 m简支波形腹板钢-混组合箱梁为实例,在最不利车道荷载作用下对其进行畸变效应分析。其组合箱梁顶板为宽3 m、厚0.25 m的C60混凝土顶板;底板为宽3 m、厚0.022 m的耐候钢底板,翼缘板为宽1.4 m、厚0.25 m的C60混凝土板;梁高h=1.82 m,其横断面见图6。波形腹板厚度tw=20 mm,a=0.33 m,b=0.27 m,h=0.2 m,混凝土的弹性模量Ec=36 MPa,泊松比υc=1.666 7;耐候钢板的弹性模量Es=210 GPa,泊松比υs=0.3。

图6 横断面图(单位:m)

首先根据截面等效原理可将钢腹板及钢底板分别转换为厚度等于94.5,120 mm的C60混凝土板,再根据箱梁横截面情况布置车道荷载,发现最不利车道荷载工况为单车道布载,单车道布载时箱梁集中畸变荷载216 kN,均布畸变荷载为6.3 kN。

当车道荷载偏心作用于波形腹板钢-混组合箱梁截面时,畸变翘正应力与畸变翘曲剪应力均在集中荷载作用的跨中位置具有最大值,且二者沿跨中向两端方向先减小后增大,受边界条件影响在梁端处趋近于0。通过对畸变应力分析发现,在车道荷载作用下产生的最大畸变翘曲正应力占弯曲正应力的14.7%,最大畸变翘曲剪应力占弯曲剪应力的48.9%。对于波形腹板钢-混组合箱梁而言,由于畸变产生的翘曲应力在梁体组合应力中的占比较大,因此在结构设计中应对畸变效应加以重视。畸变翘曲应力沿梁轴线变化曲线图见图7。

图7 畸变翘曲应力沿梁轴线变化曲线

为研究混凝土顶板厚度对波形腹板钢-混组合箱梁畸变翘曲应力的影响,保证其他参数不变的前提下,将箱梁跨中截面顶板混凝土厚度由0.15 m增至0.25 m。顶板厚度对畸变翘曲应力的影响曲线图见图8。

图8 顶板厚度对畸变翘曲应力的影响曲线

由图8可见,随着混凝土顶板厚度的增大,箱梁因畸变效应产生的翘曲正应力逐渐减小,翘曲剪应力虽然略有增大,但增幅较小,整体趋于平稳。按照波形腹板钢-混组合箱梁相关施工规范要求,一般混凝土板的施工允许误差为±5 mm,但从上述结果可知,混凝土顶板的负差将导致畸变翘曲正应力的增大,因此,在实际施工过程中,应尽量保证混凝土顶板不产生负差。

桑园子黄河大桥波形腹板钢-混组合箱梁为钢底板箱梁,设计中采用剪力钉结合底板浇筑铺底混凝土的形式来增加截面刚度。为揭示铺底混凝土厚度对箱梁畸变效应的影响规律,在保证其他参数不变的情况下,将铺底混凝土厚度由0 m增至0.3 m。铺底混凝土厚度对畸变翘曲应力的影响曲线图见图9。

图9 铺底混凝土厚度对畸变翘曲应力的影响曲线

由图9可见,随着铺底混凝土厚度的增加,畸变翘曲正应力与畸变翘曲剪应力逐渐减小,当混凝土厚度从0增至0.15 m时,翘曲正应力减小55.3%,翘曲剪应力减小71.1%。但是随着厚度的增加,翘曲应力的减小幅度也在减小,当混凝土厚度从0.15 m增至0.3 m时,翘曲正应力减小33.4%,翘曲剪应力减小46%。这说明增加铺底混凝土厚度虽然能够有效减弱箱梁的畸变效应,但随着厚度增加其效果逐渐减弱。

5 结论

1) 本文重新定义畸变角,使得畸变翘曲位移与约束扭转翘曲位移在表达式形式上具有一致性,然后基于势能驻值原理推出畸变控制微分方程,为波形腹板钢-混组合箱梁畸变效应分析提供了与扭转分析相统一的方法。

2) 畸变翘曲应力相对于弯曲应力而言不容忽视,在实际工程中对于波形腹板钢-混组合箱梁的影响较大,在结构设计过程中应充分考虑畸变效应,增加组合箱梁截面框架刚度。

3) 畸变翘曲正应力随波形腹板钢-混组合箱梁顶板混凝土厚度的增大而减小,因此在实际工程中应避免厚度小于设计值。

4) 波形腹板钢-混组合箱梁钢底板增铺混凝土时,畸变翘曲应力随铺底混凝土厚度的增大而减小,因此在设计中加设剪力钉铺设铺底混凝土能够有效提高组合箱梁的截面框架刚度,减小翘曲应力。