基于Burger’s 蠕变模型的采矿车行驶海底稀软底质下陷研究

赵化淋，孙永福，贾超，卫如春，邓浩，吴滔

1. 山东大学海洋研究院，青岛 266237

2. 山东大学海洋地质与工程研究所，青岛 266237

3. 国家深海基地管理中心，青岛 266237

随着对深海的不断探索，丰富的海洋矿产资源成为科学家关注的重点。遍布于各大洋底的多金属结核是锰、铜、镍、钴等多种金属的重要来源，研究表明其具有巨大的储量规模和经济价值[1]。据统计，全球大洋约15%的面积被多金属结核所覆盖[2]，而太平洋C-C 区、西北太平洋海山盆地、中印度洋海盆等多金属结核富集区大多赋存于低承载力与抗剪强度的稀软底质中[3-5]。伴随着南海海洋勘探深入，我国在南海多个海域发现了多金属结核成矿区，大量陆源物质进入海洋也为南海北部边缘海结核提供了丰富的成矿物质来源，便于南海边缘海结核的快速生长成矿，作为极具潜力的海洋矿产资源，南海北部多金属结核成矿区成为试验目标靶区，是目前国内深水资源勘探、开发的重点区域[6]。但铁锰结核主要分布在海底有松软沉积物的表面或者向下几厘米的表层沉积物中，开采起来较为困难[7]。深海采矿车是实现深海矿产资源开采的重要环节，由于深海沉积物不同于陆地底质，是一种具有高含水率、高液限、高塑性、大孔隙比、低强度等特性的特殊稀软底质[8]，在采矿作业中，深海稀软底质的物理力学特性极易影响采矿车行走的稳定性，较低的承载力会使得采矿车具有下陷的风险，导致采矿车不能行走或者丧失采矿功能，严重时可能会使整个采矿系统瘫痪。因此，研究海底稀软底质的物理力学特性对深海采矿车行驶下陷的影响具有重要意义，可为未来实现深海矿产的开采和利用提供必要的经验积累和技术储备[9]，同时为类似稀软底质区提供借鉴与参考。

目前，已有学者针对深海采矿车进行了广泛的研究。如Leng 等[10]研究了深海采矿车的动态特征，包括动态建模方法、轨迹特征和采矿采集系统。讨论了考虑深海沉积物对深海采矿车性能的相互作用。Schulte 等[11]通过一定比例的膨润土与水模拟海底地质的物理力学特性，研究该模拟底质在不同剪切装置下的剪切应力－位移关系，分析了采矿车深海行走性能，计算了细软底质可提供的牵引力以及采矿车的静态与动态沉陷。Hong 等[12]建立了履带式采矿车在海底稀软底质上行走的3D 瞬态模型，通过压力-沉陷、剪切应力-位移和剪切应力-动态沉陷等关系式描述了稀软底质对履带车的作用力，对履带式采矿车直线行驶与转向行驶性能进行了动力学分析。戴瑜等[13]通过构建海底履带车行驶牵引性能的数学计算模型，探明了履带车海底行走牵引力与滑转率之间的定量关系，研究了履带车接地段参数对其牵引力的影响特性，提出了履带式采矿车海底行走最佳滑转率、滑转率控制范围及履带接地参数的最佳设计值。陈峰等[14]考虑了海底履带机器车的特殊工作环境，以及车体的特殊设计，建立了海底履带机器车的数学模型，使用了MADYMO 多刚体动力学仿真软件，建立了深海底履带机器车结构模型，进行了仿真分析，并与实验结果进行了比较，验证了模型的有效性。Qi 等[15]建立了描述海底土壤流变特性的分数阶导数Burger’s模型，并通过太平洋C-C 矿区模拟土壤蠕变试验确定了其关键参数。预测了DSMV 的履带接触地面长度和行走速度，为提高采矿效率提供了安全设计。

深海稀软底质具有多孔性、高含水率和低剪切强度等力学特性且呈流动态，深海采矿车在其床面行走，容易产生随时间变化的沉陷现象，因此，研究中应考虑深海稀软底质的蠕变特性。此外，土体所表现出的物理力学性质，其根本都是内在结构发生变化的外在反映，结构性对土的性质的变化起着重要的决定作用，缺乏对土体结构特征及其演化规律的描述会导致实际的工程计算结果难以模拟土体的实际状态，进而出现较大的计算误差，故而原状土的结构性对研究结果具有重要意义[16]。综上，前人的研究要么没有考虑海底稀软底质的蠕变特性，要么仅采用模拟土样来模拟海底底质的物理性质，缺乏原状土的结构性，因此均具有一定的局限性。

考虑到深海稀软底质的蠕变特性，Burger’s 模型作为常用的蠕变模型之一，可反映稀软底质的黏弹性特点。因此选用PFC3D 颗粒流数值模拟软件为研究手段，以其中Burger’s 接触模型作为海底稀软底质的本构模型，进行模拟研究。软件中模型接触力按时间步长不断进行迭代，模拟应力变形随时间的发展过程，从而迭代计算稀软底质的非恒定荷载作用。以某海域稀软底质原状土为依托，开展土工试验与室内三轴试验，获取其物理力学性质，并通过室内三轴试验与模拟三轴试验对PFC3D 中Burger’s 接触模型进行参数标定。依据标定结果，改变相应参数从而获得不同底质条件的5 种工况，针对5 种工况建立了采矿车在海底稀软底质地层上行走的数字仿真简化模型，通过计算模型研究了各工况下海底采矿车在不同行驶速度时的下陷深度，从而分析海底采矿车在稀软底质的行驶稳定性，在宏观上做一般的探讨，为类似参数的海底稀软底质的采矿车行驶提供借鉴与参考。

1 研究方法

1.1 Burger’s 蠕变本构模型

对海底稀软底质选用Burger’s 蠕变模型，通过开尔文模型（Kelvin）和麦克斯韦模型（Maxwell）在法向和剪切方向串联来模拟蠕变机制。开尔文模型是线性弹簧和阻尼元件并联作用的组合，麦克斯韦模型是线性弹簧和阻尼元件串联作用的组合。伯格的模型作用于一个很小的区域，因此只传递一种力。

在法向和剪切方向上，Burger’s 模型的蠕变组分如图1 所示，该模型将开尔文模型和麦克斯韦模型串联起来。

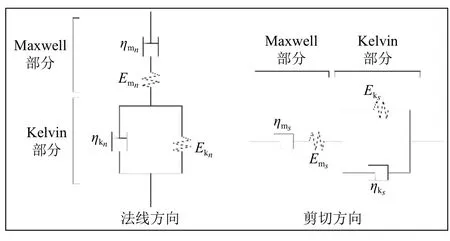
图1 Burger’s 蠕变模型Fig.1 The Burger's creep model

在法线方向上，麦克斯韦模型提供了刚度为Emn的线性弹簧和黏性系数为ηmn的阻尼器，开尔文模型提供了刚度为Ekn的线性弹簧和黏性系数为ηkn的阻尼器。在剪切方向上，麦克斯韦模型提供了一个刚度为Ems的线性弹簧和一个黏性系数为ηms的阻尼器，开尔文模型提供了一个刚度为Eks的线性弹簧和一个黏性系数为 ηkn的阻尼器。基于该本构模型，石崇等[17]在《颗粒流（PFC5.0）数值模拟技术及应用》中给出颗粒间接触力。

在每个方向上，Burger’s 模型的总位移u为模型的开尔文部分位移uk和麦克斯韦部分位移umE、umη三者之和，如公式1 所示：

式1 关于时间t的一、二阶导数分别如公式2、公式3 所示：

接触力F，利用模型中开尔文体的刚度Ek、黏性系数 ηk和一阶导数，由公式4 给出，同时，其一阶导数F˙如公式5 所示：

式中，符号 ±分别表示法线方向和切线方向， +表示法线方向， -表示切线方向。同样，利用麦克斯韦体的刚度Em和黏性系数 ηm，给出接触力F及其一、二阶导数

综上，可求得接触力F的二阶微分方程如公式7：

由公式7 可知，Burger’s 蠕变模型的本构模型如公式8 所示：

式中， σ为应力； ϵ为应变。

1.2 基于离散单元法的Burger’s 模型

连续介质理论中的Burger’s 模型将试样视为连续体，模型作用的对象是整个连续的试样[18]。而在颗粒离散单元法中，当前时步颗粒间的接触力是根据上一时步的接触力值以及当前和上一时步颗粒间发生的位移来更新的，因此，接触力可采用有限差分法进行计算。石崇等分别对模型中开尔文体以及麦克斯韦体的接触力和位移进行了公式推导，同时根据黏弹性线性叠加原理给出总位移[17]。

1.2.1 模型中的开尔文体

对于模型中的开尔文体，其为线性弹簧和阻尼器并联构成，因此，位移与接触力之间的关系可由公式9 表示[19]：

采用中心差分方式近似求取uk和F的平均值，可得：

式中，t表示当前时步的计算结果；t+1 表示下一时步的计算结果； Δt为时间步长。

对公式10 进行整理，可得到公式11 所示开尔文体位移的计算公式：

式中，A、B为关于时间步长的函数，可分别由公式12、公式13 求得：

1.2.2 模型中的麦克斯韦体

对于模型中的麦克斯韦体，其为线性弹簧和阻尼器串联构成，因此，其位移及位移的一阶导数分别为公式14、15 所示：

将公式6 代入公式15 可得：

同样地，采用中心差分方式近似求取um和F的平均值，可得：

对公式17 进行整理，可得到麦克斯韦体位移的计算公式18：

1.2.3 整个Burger’s 模型

对于整个Burger’s 模型，根据黏弹性线性叠加原理，总位移u可由公式19 给出：

对公式19 进行中心差分近似，可得：

综上可得，最终接触力计算公式如公式21 所示：

式中，C、D为关于时间步长的函数，可分别由公式22、23 求得：

2 微观参数标定

本研究采用PFC3D 颗粒流数值模拟软件中的Burger’s 接触模型作为海底稀软底质的本构模型进行模拟研究，为得较符合实际的数值模拟结果，数值模型的微观参数应与材料的宏观力学特性相互对应。石崇等[17]给了一种基于三轴试验的Burger’s接触模型参数的标定方法，是一种较为理想并应用广泛的进行颗粒微观参数标定的校准方法。本节通过在PFC3D 中模拟常规三轴压缩实验，同时开展室内常规三轴试验，基于微观参数与宏观参数的关系，对微观参数进行调试，从而使数值模拟试验与室内三轴试验所表现出的宏观力学特性保持一致。

2.1 模型参数影响

在颗粒离散单元法中，Burger’s 蠕变模型共有9 个基本参数，如表1 所示。

为了明确每个参数对瞬时强度特性以及蠕变特性的影响，杨振伟等[18]在PFC3D 中建立了常规三轴压缩实验的数值模型，在模拟试验中采用控制变量法对每个参数进行了分类研究。为方便计算，对各个参数的法向和切向设置了相同的参数值，从而将Burger’s 接触模型参数简化为5 个，即Em、ηm、Ek、ηk和f。

2.1.1 模型参数对瞬时强度特性的影响

取弹性模量、泊松比、单轴抗压强度等三项物理力学参数作为反应瞬时强度特性的指标，通过5 组对比试验得到了不同模型参数取值下相应的瞬时强度结果。模型中各参数对瞬时强度特性的影响关系如表2 所示。

表2 Burger’s 蠕变模型参数对瞬时强度特性的影响Table 2 The effect of Burger’s creep model parameters on instantaneous strength characteristics

由试验结果可知，在Burger’s 蠕变接触模型中，仅有Maxwell 体弹性系数和摩擦系数对瞬时强度特性存在显著影响，其余参数均对瞬时强度特性无显著影响。因此，在进行Burger’s 蠕变模型参数标定调试时，只需调试Maxwell 体弹性系数和滑动摩擦系数即可，对其他参数可直接匹配无需调整。

2.1.2 模型参数对蠕变特性的影响

同样地，通过对比试验记录在不同模型参数取值下轴向应变随时间的改变量，得出各模型参数不同取值情况的蠕变加载、卸载曲线。取瞬时应变量、起始应变量、起始应变率等八项参数作为反映蠕变特性的指标，模型中各参数对蠕变特性的影响关系如表3 所示。

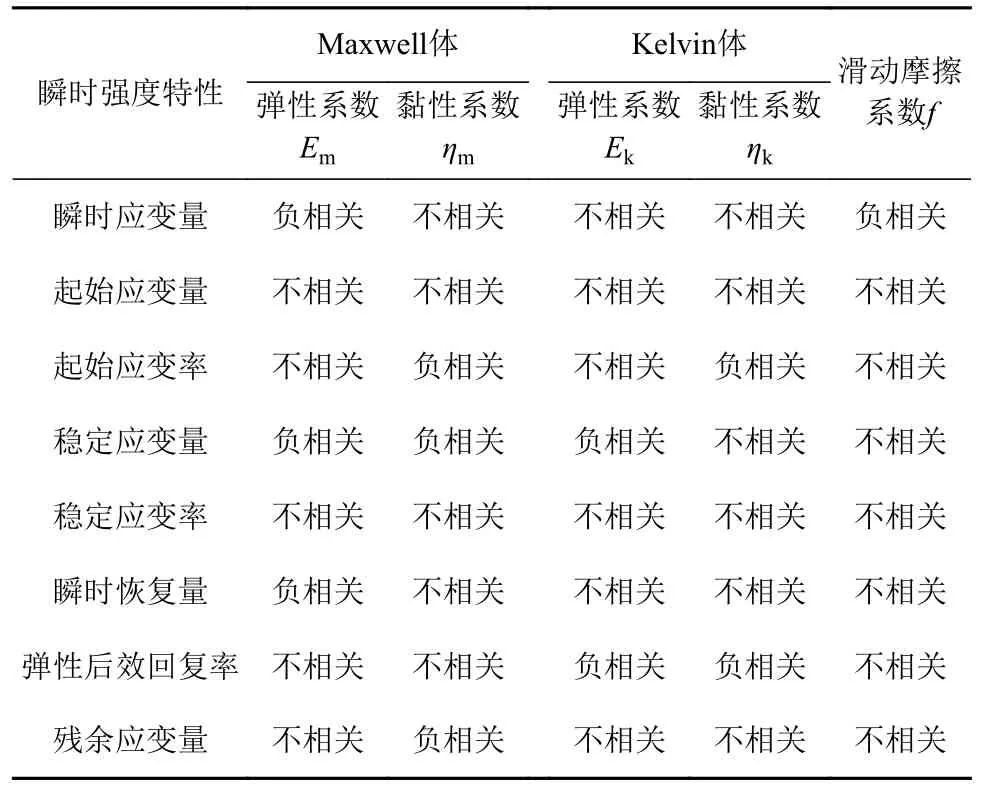
表3 Burger’s 蠕变模型参数对蠕变特性的影响Table 3 The effect of Burger’s creep model parameters on creep characteristics

试验表明，材料在经历短暂初始顺势变形后，开始进入等速蠕变阶段，此后应变增加速率随时间增长逐渐变小并趋于0；卸除偏应力，变形将急剧减小，但随着弹性应变的不断恢复，应变减小速率逐渐变小并最终趋于稳定。

不同模型参数下的蠕变特性表明，Maxwell 体的弹性模量与瞬时应变量、瞬时恢复量，黏性系数与稳定蠕变率、残余应变量呈负相关关系；Kelvin体的弹性模量与起始蠕变量，黏性系数与起始蠕变率、弹性后效恢复率呈负相关关系；滑动摩擦系数则与瞬时应变量呈负相关关系。

2.2 物理标定试验

2.2.1 试验仪器及材料

试验仪器采用德国APS-WILLE Geotechnik 伺服电机控制动三轴试验系统，该试验系统是由电机加载系统、三轴室及升降装置、自动体积压力控制器（VPC）、动态控制器以及计算机等部分组成（图2）。

图2 伺服电机控制动三轴试验系统Fig.2 The system of servo motor-control dynamic triaxial test

动三轴试验仪加载活塞能补偿在动态和静态试验期间由于三轴室内部的加载杆的体积变化而导致的围压变化，可以准确控制轴向和围压之间的相位。电机作动器与操作软件相结合，能够生成并施加不同类型的加载波形到试样，最大荷载可达60 kN，荷载精度为0.1% F·S。三轴室采用可更换的上帽和底座，适用于直径为38 ～150 mm 的试样。

试验材料为某区域海底底质原状土样，土样采用特定密封容器保存，同时在封口处用保鲜膜困扎密封。运输过程中按原状方向放置，加固容器以防止土样在运输过程中受到振动、冲击或其他影响，同时避免在运输过程中暴露土样于高温、高湿度等不适宜环境中。

采用Mastersizer 3000 激光粒度分析仪对海底沉积物土样进行粒度分析，结果表明，沉积物中砂砾占2.3%～5.2%，黏粒占 38.1%～48.4%。采用多功能X 射线衍射仪对沉积物进行矿物成分分析，沉积物土样主要由石英、白云母、方解石、钠长石和绿泥石等矿物组成。其中，石英占40.9%，白云母占29.3%，方解石占22.7%，钠长石占6.5%，绿泥石占0.6%。

采用GYS-2 型液塑限测定仪、ZJ 四联应变控制式直剪仪、WG 型单杠杆固结仪等试验仪器，对海底沉积物土样进行天然含水率及天然密度试验、液塑限试验、四联剪切试验、固结压缩试验等室内试验。

根据室内土工试验结果，同时综合现场调查数据，得到所示该土样所处海域海底底质物理力学性质范围（表4）。

表4 研究海域海底底质物理力学性质范围Table 4 Physical and mechanical properties of seabed sediments in the study area

由试验结果可知，该海域海底底质土样具有较高的含水率、液限、可塑性和压缩性，具有更低的密度和强度特性。

2.2.2 试验内容及结果

常规三轴试验是较为理想的进行颗粒细观参数标定的基准试验，其作用只是为了对数值模拟中的微观参数进行标定，理论上保持数值模拟三轴试验与室内常规三轴试验二者的试验条件相对应，即可进行对微观参数的标定。因此本次研究选取固结排水试验，对3 组南海原状土进行了不同围压的三轴压缩试验。试验土样为圆柱形试样，试样尺寸为直径×高度=38 mm×76 mm，剪切类型为固结排水剪切，3 组围压分别为100、150、200 kPa。采用等应变速率剪切，考虑到剪切类型为固结排水剪切，根据《土工试验方法标准》（GB/T 50123—2019），剪切速率宜为0.003%/min～0.012%/min。试样轴向尺寸为76 mm，选取加载速率为0.008 mm/min[20]。具体试验方案如表5 所示。

从数据中来，到实践中去。全面质量管理，控制病种成本，促进学科发展，推进医师执业能力评价。破旧立新，腾笼换鸟，病种分析引领医院精细化管理。

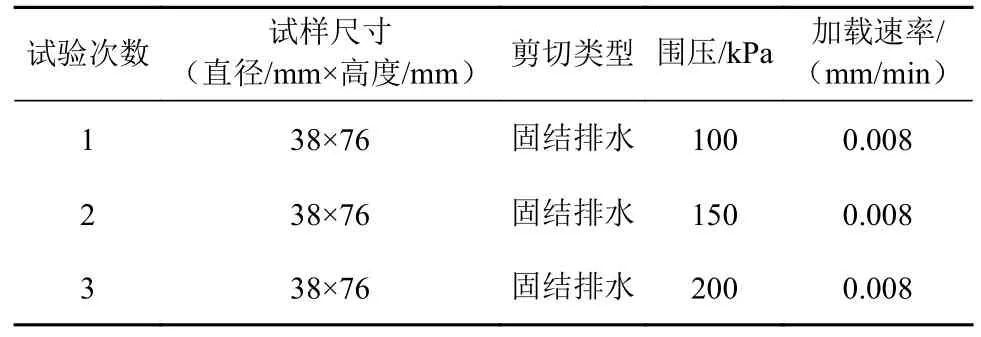
表5 三轴试验方案Table 5 Triaxial test scheme

根据《土工试验方法标准》（GB/T 50123—2019），具体试验步骤如下：

（a）该原状土为较软土样，采用切土盘削切成直径为38 mm 的圆柱形土样，取试样高度为76 mm，按要求削平上下两端。放入饱和器在水下静止饱和10 h。

（b）在压力室底座依此放置透水石、滤纸、试样、滤纸、透水石以及试样帽，用橡胶膜套在试样外并扎紧在压力室底座及试样帽上。安装压力室罩并注水，对试样施加相应围压进行固结。

（c）固结完成后，按照试验方案选取的加载速率进行轴向加载，直至试样达到设定的轴向应变。

（d）在不同围压条件下，完成三组三轴压缩试验，提取试验数据并分析，得到不同围压条件下的应力应变曲线（图3）。

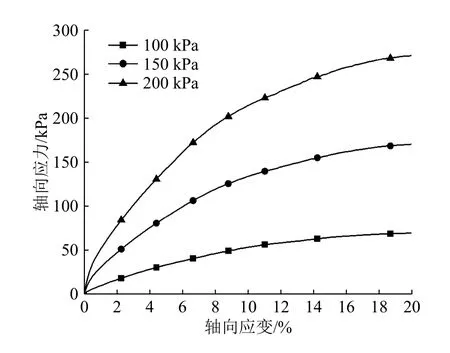
图3 不同围压条件下的应力-应变曲线Fig.3 Stress-strain curves under different confining pressures

2.3 微观参数标定

2.3.1 数值模型建立

数值模拟采用PFC3D 颗粒流软件，为减少颗粒数量，提高计算速度，三轴试验数值模拟中颗粒的尺寸相比于实际颗粒粒径有所放大。Huang 等[21]指出，在三轴试验的离散元模拟中，当尺寸比SR（即试样最小边长与颗粒中值粒径的比值）相对较小时，会引起边界效应，而根据河海大学石崇等专家的研究结果可知，当尺寸比SR＞40 时，试样尺寸对数值计算结果的影响可忽略不计[22]。

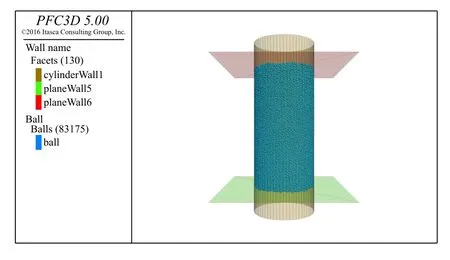
图4 常规三轴试验数值模型Fig.4 Numerical model of conventional triaxial test

侧面作为伺服控制平面，通过控制其收缩和扩张对模型试样施加整体围压并在伺服机制下保持围压的恒定。上下两墙体作为加载板，可以沿模型试样轴向方向上下移动，可通过定义上下加载板的移动速度来实现等应变速率的固结排水剪切试验。

2.3.2 数值模型参数标定

数值模型生成后，根据表4 研究海域海底底质物理力学性质范围，定义模型的颗粒密度等已知参数。对模型中颗粒间的接触定义为Burger’s 接触模型，为方便计算，同样对各个参数的法向和切向设置了相同的参数值，从而将Burger’s 接触模型参数简化为5 个。标定之前，同样根据表4 中粘聚力、内摩擦角、压缩模量等参数，对5 个基本参数初步赋予相应的经验值。

参数赋予后，通过伺服控制平面对模型试样施加相应恒定围压，实现试样的各向同性固结，固结过程中保持排水条件。固结完成后，对加载板施加等同于室内三轴试验的加载速度进行压缩试验，试验结束后输出应力-应变曲线。

根据首次试验得到的应力-应变曲线，并按照本文第2.1 节中的参数调试方法对5 个基本参数进行调试。经调试后，所采用的模型微观力学参数如表6所示。且不同围压下室内三轴试验与数值模型三轴试验所得应力-应变曲线对比结果如图5 所示。

表6 模型微观力学参数Table 6 Micromechanical parameters of the model

图5 室内试验与数值模拟对比结果Fig.5 Results of comparison between laboratory test and numerical simulation

根据对比结果可以看出，数值模拟结果与室内试验结果较为吻合，因此，可以用该参数作为Burger’s 接触模型的微观参数取值，同时根据该结果亦可论证选用Burger’s 蠕变模型的合理性。

2.4 不同工况下模型参数取值

根据表2、3 中蠕变模型参数分别对瞬时强度特性以及蠕变特性的影响机制，依据上述标定结果，改变不同模型参数获得不同底质条件的5 种工况，从而研究不同底质条件下采矿车行驶的下陷情况。对应工况下的模型参数取值如表7 所示。

表7 不同工况下的模型微观力学参数Table 7 The micromechanical parameters of the model under different working conditions

3 海底采矿车行驶数值模拟

3.1 计算模型

本文采用鲲龙500 深海采矿车为模型原型，采矿车整体结构如图6 所示，长5.4 m，宽3.5 m，高1.9 m，在陆地上总重9.5 t。

图6 鲲龙500 深海采矿车Fig.6 Kunlong 500 deep-sea mining vehicle

利用PFC3D 软件中的Clump 模块生成采矿车的简化模型，履带触地尺寸为0.8 m×4.6 m。通过赋予Clump 模块体积、密度等参数，从而达到计算模型模拟采矿车整车质量以及通过履带对土体产生相应压力的效果，三维简化模型如图7 所示。

图7 深海采矿车三维简化模型Fig.7 3D simplified model of a deep-sea mining vehicle

按上述三轴试验数值模型的参数生成海底土层模型，由于计算能力的限制，在海底采矿车行驶模拟中，海底底质颗粒粒径同样有所放大。取尺寸比SR 为40，按同比例的粒径级配修改数值模型中的粒径级配为0.07～0.18 m，最终生成尺寸为10 m×20 m×10 m 的海底地层模型。定义颗粒间的接触为Burger’s 接触模型，赋予表7 中不同工况下的接触模型参数。

施加流体单元，打开渗流模块和浮力计算选项，读取流体单元的节点文件和单元构成文件，设置流体单元的密度为1 040 kg/m3，流体动力粘滞系数为1×10-3Pa·s，施加流体单元压力，定义静水压力。施加重力场，在重力和浮力作用下进行地层平衡，得到海底地层计算模型（图8）。

图8 海底地层计算模型Fig.8 Computational models of the sea bottom

调用采矿车三维简化模型，在重力和浮力作用下下沉到地层表面，与地层接触，得到采矿车海底行驶计算模型（图9）。

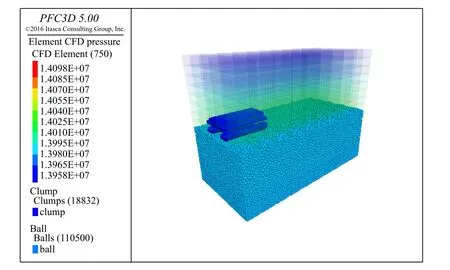
图9 采矿车海底行驶计算模型Fig.9 A computational model of mining car undersea driving

履带式采矿车在海底移动的实际速度通常为0.5～1.0 m/s[14]，因此本研究采用0.5、1.0、1.5 以及2.0 m/s 的速度进行仿真计算，模拟不同工况下采矿车在不同行驶速度中的下陷情况。同时，取速度为0，模拟静止情况下的下陷情况。

3.2 颗粒与流体耦合作用分析

PFC 中颗粒与流体之间的运算是通过差分方法实现的[23-26]，其指导思想是将颗粒与流体之间的相间作用力作为固相与液相之间的桥梁，通过该作用力在两相之间建立联系，在整个计算过程中，通过渗透介质变化反映流场的变化，进而不断更新相间作用力。

液相与固相之间的相互耦合过程如图10 所示，整个计算域内，颗粒采用离散介质方法从微观尺度进行研究，流体基于连续介质方法从中尺度层面考虑其平均值[27]。

图10 固相与液相耦合过程示意图Fig.10 Schematic diagram of solid-liquid phase coupling process

图10 中，首先按孔隙率生成颗粒，引入流场，并通过计算使得颗粒处于稳定状态。在当前时步，按照颗粒的位置决定颗粒之间重叠量，从而计算颗粒间的接触力，并将该接触力施加到颗粒的运动方程；另一方面，根据颗粒的分布确定流体计算单元内的孔隙率，根据初始条件和边界条件以及获得的单元孔隙率将流体方程进行离散求解，计算该时刻的流场，经迭代稳定后，获取各流体单元的压力梯度，用于计算固相与液相之间的相间作用力，将此作用力作为颗粒受到的外力施加到运动方程。颗粒在内外力作用下会产生新的加速度、速度、位移，颗粒位置重新调整，再由力-位移法则得出下一时步颗粒间的接触力，根据颗粒分布确定下一时步流体单元的孔隙率，将其代入流体方程，如此反复，从而实现颗粒与流体之间的耦合计算。

基本模拟过程如下：① 生成墙体和颗粒；② 设置墙体和颗粒属性；③ 读入流体网格；④ 设置流体属性；⑤ 循环求解。

3.3 计算结果与分析

图11 所示不同工况下海底采矿车在不同车速下的下陷情况。由下陷曲线得出不同速度工况下采矿车稳定时间与稳定下陷量（表8）。

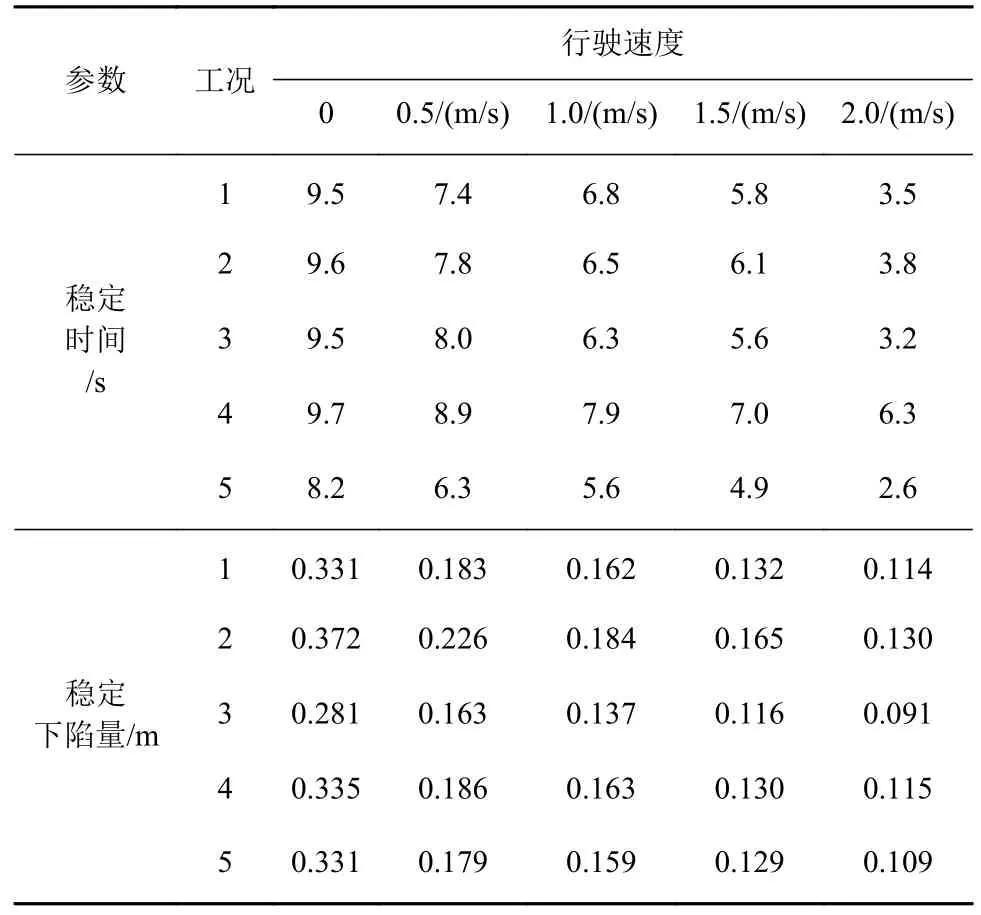
表8 不同工况下采矿车各行驶速度的下陷数据Table 8 Subsidence data of a mining car at different driving speeds under different working conditions

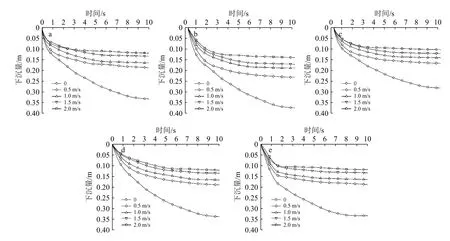
图11 各工况下不同车速下的下陷曲线a:工况1, b: 工况2, c: 工况3, e: 工况4, d: 工况5。Fig.11 Subsidence curves at different vehicle speedsa: Condition 1, b: Condition 2, c: Condition 3, d: Condition 4, e: Condition 5.

对于土样所处海域，由工况1 曲线可知下陷情况分为两个阶段：0～0.5 s 时在初始装载期间发生的瞬时下陷，以及0.5 s 后发生的蠕变下陷。且由其他工况曲线可知，不同底质条件下的下陷情况均可大致分为以上两个阶段。

进一步分析可知，对于同一种底质条件，海底采矿车在静止时下陷量最大，随着采矿车行驶速度的增加，其下陷量会随之减少并趋于稳定；蠕变随时间的变化而变化，当海底采矿车行驶速度更快时，海底稀软底质的蠕变时间减少，从而导致蠕变下陷量减小。对于不同底质条件，对比图11a、b、c 可知，较大弹性系数的底质其下沉量较小，即具有较强的承载力；对比图11a、d、e 可知，较大黏性系数的底质其下陷稳定时间较短，蠕变时间较少，即具有较低的蠕变性能。

本次研究中海底采矿车行驶的模拟下陷趋势与Bekker[28]在1969 年的研究结论一致，因此，采用基于Burger’s 蠕变模型的PFC 颗粒流软件是可行的，本次研究具有一定的可靠性。

Xu 等[29]于2016 年通过制备人工材料来模拟太平洋多金属结核矿区的深海稀软沉积物的性质，进行了不同压应力下的压缩蠕变试验和不同压剪应力下的剪切蠕变试验，从而获得压剪蠕变参数，建立了压沉模型和压剪复合蠕变本构模型，利用RecurDyn 软件计算了履带式矿车在不同速度时的压剪复合蠕变下陷。对比其结果，本次研究获得了一致的蠕变下陷趋势，进一步验证了本研究的可靠性。

4 结论

（1）本文以某海域海底稀软底质原状土样为依托，开展了相关土工试验，综合现场调查资料得到了海底稀软底质的物理力学性质范围：物理性质中，天然含水率为88.13%～137.79%，天然密度为1.3～1.5 g/cm3，孔隙比为2.46～3.85，液性指数和塑性指数分别为0.96～1.97 和37.2～57.8；力学性质中，粘聚力为3.7～6.9 kPa，内摩擦角为2.4°～3.9°，压缩系数为1.86～3.73 MPa-1，压缩模量为1.26～2.13 MPa，贯入阻力为0.19～1.32 N。试验结果表明，该海域海底稀软底质具有更高的黏粒含量、含水率和压缩性，具有更低的密度和强度特性，即承载力较低，蠕变性能较强。同时为进一步进行不同底质条件下海底采矿车在不同行驶速度时的下陷深度研究奠定了数据基础。

（2）模拟结果显示，对于同一种底质条件，下陷量会随时间呈非线性的变化，除装载期间发生的瞬时下陷外，约0.5 s 后会因海底底质的蠕变性能而发生蠕变下陷，并逐渐趋于稳定；且稳定时间与行驶速度呈负相关，行驶速度越快，蠕变下陷量达到稳定时所用时间越少；就不同行驶速度而言，蠕变下陷量与行驶速度呈负相关，当行驶速度更快时，海底底质的蠕变时间减少，从而会导致蠕变下陷量的减小。

（3）对于不同底质条件，对较大弹性系数的底质其下沉量较小，即具有较强的承载力；较大黏性系数的底质其下陷稳定时间较短，蠕变时间较少，即具有较低的蠕变性能。