基于BP神经网络的海底浅层超软黏土不排水抗剪强度预测*

孙 耀 李 飒 李怀亮 甘惠良 赵福臣

(1. 天津大学建筑工程学院 天津 300350; 2. 海洋石油工程股份有限公司 天津 300461)

南海蕴藏了丰富的油气资源[1-2],但该海域海底表层沉积物类型复杂,现有研究显示,存在以黏土为主的海底表层土,颗粒极细,含水量很高,不排水强度小于5 kPa[3],本文将其称为超软黏土。超软黏土因其强度低、松软易变形的特性很容易引发海底失稳[4],所以其力学特性需要特别关注。处于海底表层的饱和超软黏土的状态介于固体与流体之间,因此很难取得高质量的原状样,依靠室内试验准确确定其不排水强度存在困难[5];对于原位试验CPT,现有研究显示,利用CPT数据反演0～5 m范围的土体分类及性质误差较大[6]。这使得合理、快捷地得到浅层超软黏土的不排水抗剪强度成为研究人员关注的焦点[7]。

已有研究表明,黏土的不排水抗剪强度与其自身物理性质密切相关。目前,主要采用回归分析方法,建立某些物性指标与不排水抗剪强度的关系式来获取超软黏土的不排水抗剪强度。研究者通过多种试验方法发现,不排水抗剪强度与含水率[8]、液性指数[9]、流动性指标[10-11]、含水量比[12-15]等多种因素都存在着联系。

近年来,国内外一些学者开始采用机器学习方法开展土体不排水抗剪强度预测的研究。在该类方法中,神经网络能够对非线性关系进行建模,适用于土体参数之间复杂关系的表述。同样是建立黏土的不排水抗剪强度与其自身物理性质之间的联系,相较传统线性回归模型,神经网络能够更准确地捕捉数据之间的非线性关系。神经网络通过学习土体样本数据中潜在的复杂规律和关联性,能够较准确地预测未知土体样本的物理力学参数[16]。该方法在软黏土物理力学参数预测方面已经取得了一定研究进展。研究人员利用不同的数据来源和方法,如基于孔压静力触探(CPTu)现场测试数据[17]、室内不固结不排水剪切试验数据[18]等数据来源,再通过RBF神经网络[19]、灰色关联-径向基神经网络[20]等方法,建立了多种神经网络模型来预测软黏土的力学特性和物理参数。这些研究为软黏土物理力学参数的预测提供了重要理论支持和技术手段。

为了建立中国深海超软黏土的不排水强度与物理性质指标的关系,本文采用落锥法对超软黏土的不排水强度进行了测试。考虑到现有研究得到的不排水强度与各类物性指标之间的关系离散性较大,通过已有地区黏土试验数据,建立的单一指标关联经验公式普适性较差。因此,本文尝试通过收集多地区黏土试验数据,建立不排水抗剪强度与物性指标之间的非线性映射网络来预测超软黏土的不排水抗剪强度,即利用BP神经网络反演各物性指标与不排水抗剪强度关系,对超软黏土的不排水抗剪强度进行预测。同时,根据建立的神经网络模型以权积法求解抗剪强度对各物性指标的敏感度系数,从而评价各项指标对不排水抗剪强度的影响程度。基于这种评价,根据试验与搜集的数据给出了针对中国海域超软黏土的对数流动性指数与不排水抗剪强度关联的经验公式,从而为实际工程提供参考。

1 现有经验公式对海底浅层超软黏土不排水强度的拟合情况

为了开展黏性土不排水抗剪强度反演研究,在中国南海LS场地约1 500 m水深的海底表层取得5种海底超软黏土进行了物理性质测试,试样物理性质指标见表1。

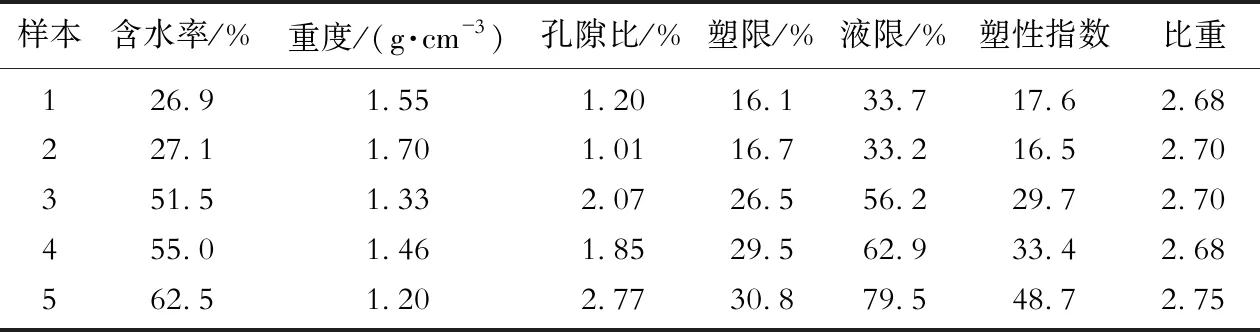
表1 南海1 500 m水深软黏土试样的物理性质指标

由于海底表层的土体强度较低,三轴试验等常规方法无法开展,目前很多国家采用落锥法进行不排水强度的测量,该方法已经列入了相应的土工试验规程[21]。落锥试验是一种根据锥重量、贯入深度和经验系数来测定黏土不排水抗剪强度的试验[22],其最小测试强度可达0.1 kPa[23]。本文采用锥角为60°,锥质量为60 g的圆锥锥头,依据规范[24]对表1土样进行不排水强度测量。由于采用扰动土进行试验,为了获得更多数据,通过阶梯式改变土样的含水量获得每个土样的多组试验样品,具体试验方案见表2。

在试验得到落锥贯入深度后,依据试验规程给出的落锥试验计算不排水抗剪强度经验公式,计算土体的不排水强度。

Su=kmg/h2

(1)

式(1)中:Su为不排水抗剪强度,kPa;k为由锥角决定的经验系数,无量纲;m为锥头质量,kg;g为重力加速度m/s2;h为落锥贯入深度,m。

为了获得更准确的数据,对上述所有样品同时进行了每组3次的平行微型十字板试验,得到不排水抗剪强度与mg/h2关系(图1)。通过十字板试验确定式(1)中k值。结果表明,当k值取0.28时,落锥预测强度与十字板试验测量强度具有较好的一致性,这与规范推荐的k=0.27非常接近[24],因此本文k取0.28进行各土样的不排水抗剪强度的计算。

图1 微型十字板试验的不排水抗剪强度与mg/h2关系

根据本次试验数据,得到Su与含水量比WCR的拟合公式,即

Su=2.178 4WCR-5.336

(2)

将式(2)和现有文献公式(表3)计算结果进行对比,可以看出,本次试验数据与Federico公式吻合度最高,但与其他公式相差较大(图2)。这主要是由于现有公式均是通过试验数据获得的经验公式,其普适性较低。为了进一步说明这一点,同时进一步扩充数据规模,通过查阅文献收集了90组取样深度在海床表面以下5 m范围内同时包含含水率、液塑限且不排水抗剪强度低于5 kPa的海洋超软黏土数据(表4、图3),这些数据遍及5个国家9个不同地区。可以看出,当取样地点不同时,数据的离散性很大,现有经验公式均无法同时反应所有数据的变化特征;且数据的高离散性,也导致很难获得精度较高的拟合公式。

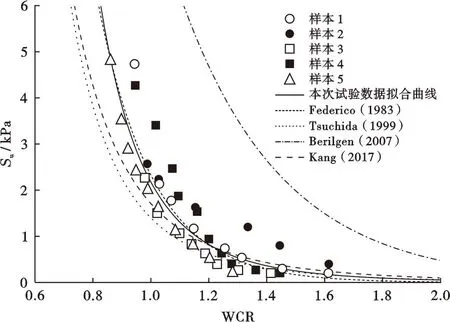
图2 不排水抗剪强度和与含水量比关系

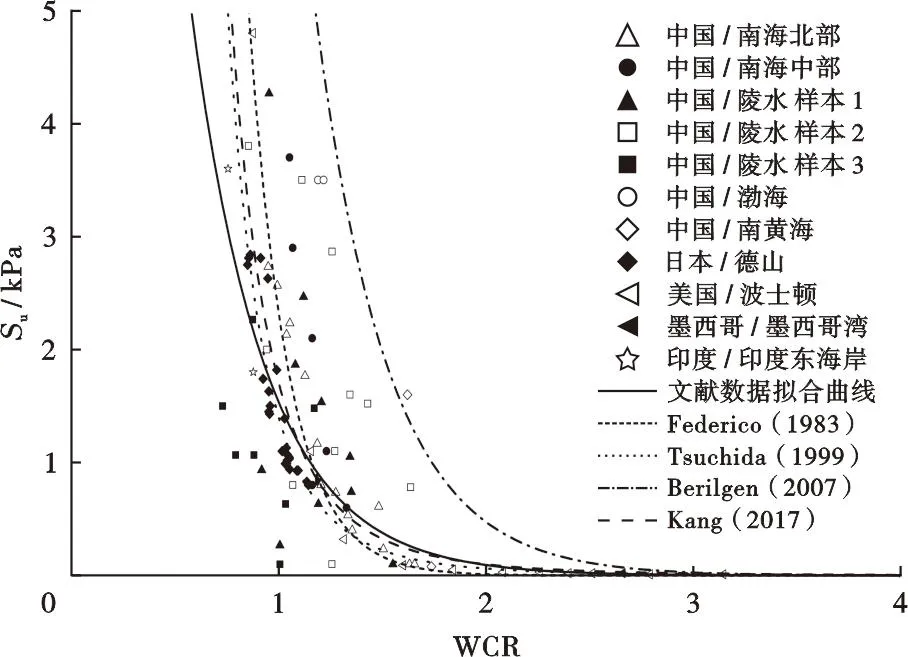
图3 现有文献数据中不排水抗剪强度与含水量比关系

表3 现有经验公式中不排水抗剪强度与物性指标关系

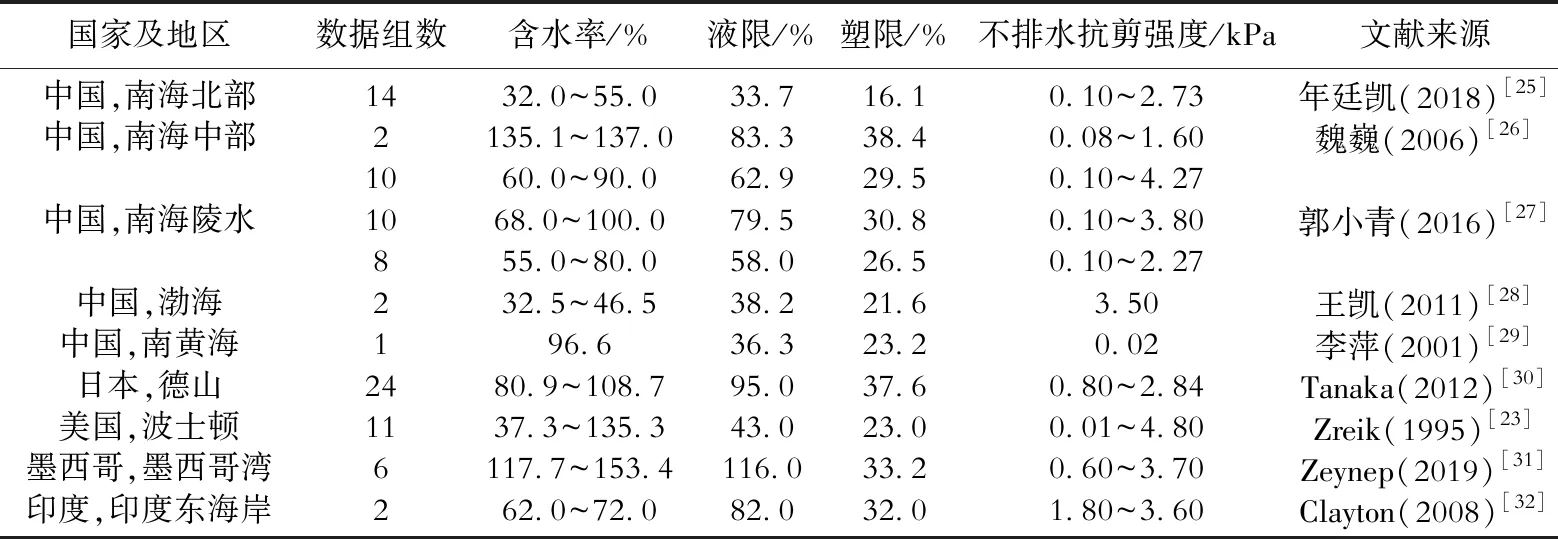
表4 不同海域超软黏土文献数据汇总

2 基于BP神经网络模型的超软黏土不排水抗剪切强度预测

2.1 BP神经网络模型

考虑不同地区黏土试验数据的高离散性,基于单一指标建立的不排水抗剪切强度拟合公式普适性较差。因此,尝试通过收集多地区超软黏土试验数据,建立土样不排水抗剪强度与物性指标间的非线性映射网络来预测超软黏土的不排水抗剪强度。本文基于python编程语言建立的不排水抗剪强度预测模型为BP(back propagation)神经网络模型,BP神经网络本质上是一种多层前馈神经网络,按照误差逆向传播的算法进行训练[33]。根据现有研究成果,BP 网络输入向量包含3个基础参量:含水率(w)、液限含水率(wl)、塑限含水率(wp);3个衍生参量:液性指数(IL)、对数流动性指数(ILN)、含水量比(WCR),输出向量为超软黏土的不排水抗剪强度(图4)。隐藏层与输出层都使用relu函数(式(3)),相对于常用的sigmoid函数,relu函数能很好地缓解梯度弥散与过拟合的问题,也能起到加快神经网络学习速度的作用[34]。

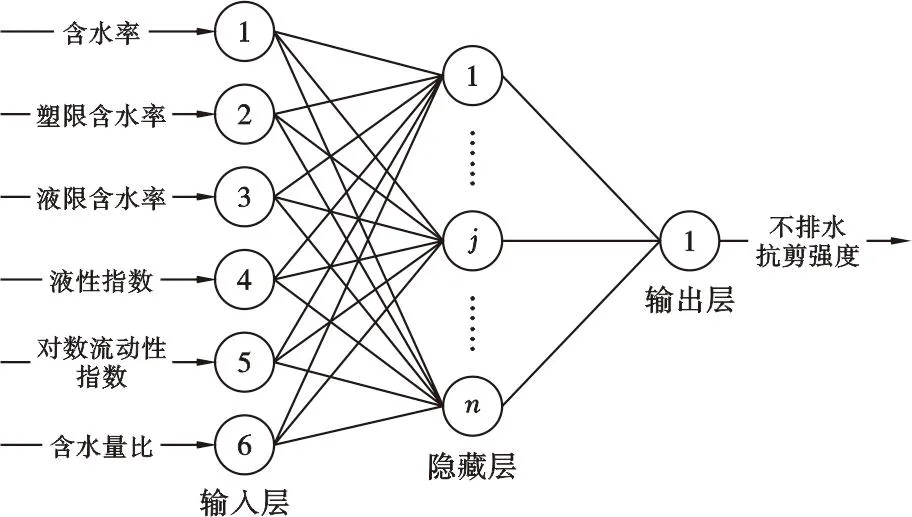
图4 BP神经网络结构图

f(x)=max(0,x)

(3)

2.2 训练、测试和验证数据

为了开展超软黏土不排水抗剪强度预测,将通过查阅文献收集的90组深海超软黏土数据(表4)作为神经网络的训练与测试组数据,并从中随机选取80组作为训练数据,另外10组作为测试数据,从基于表2测得的51组试验数据中,选择不排水抗剪强度低于5 kPa的42组数据作为神经网络的验证数据。

为了提高和保证预测精度并且方便计算,在开始训练预测模型前,将神经网络模型数据库内的不排水抗剪强度值及各物性指标参数数据按式(4)[35]全部归一化在[0.1,0.9]的区间内。

(4)

式(4)中:Xmin、Xmax分别是参数X中的最小值、最大值;Y是参数X归一化后的值。

2.3 模型结构参数选取

现有研究成果表明,超软黏土不排水抗剪强度Su与液性指数IL[9]、对数流动性指数ILN[11]、含水量比WCR[12]这3个衍生参量有较大相关性。为了合理选择输入参量,对比研究2种不同的3维输入与6维输入共3种输入模式的预测效果。其中2种3维输入模式分别为w、wl、wp,称之为三维基础组;IL、ILN、WCR,称之为三维衍生组,衍生组参量由基础组参量通过式(5)～(7)计算得到,6维输入为w、wl、wp、IL、WCR、ILN,称之为6维组。

IL=(ω-ωp)/(ωl-ωp)

(5)

ILN=ln(ω-ωp)/ln(ωl-ωp)

(6)

WCR=ω/ωL

(7)

理论上3层BP神经网络模型即可实现非线性映射,考虑到3层以上神经网络学习速度减慢的特点,本文采用单隐层神经网络。在做对比试验时,神经网络参数除了输入模式不同以外其他设置均相同。根据式(8)[36]可确定3维输入模式下的隐层节点的数量范围为2～12,6维输入模式下的隐层节点的数量范围为3～13。

(8)

式(8)中:n为隐层节点数;ni为输入参量数;no为输出参量数,本文的神经网络仅输出不排水抗剪强度,因此no取1;a为可自取的任意值变量,通常为0～10的固定值。

由网络模型在3种输入模式下的预测均方误差MSE与隐层神经元数的关系(图5),可以看出,3种输入维度下MSE均随隐层神经元数增大而先波动减小后逐渐增大,尤其是6维输入模式的波动性最大;6维组、3维基础组、3维衍生组这3种输入模式的MSE最小值分别为0.015 9、0.035 15和0.028 47,与之相应的隐层神经元数为9、6、6个。可见,衍生组的MSE最小值比基础组更小,这与现有研究成果相吻合。得益于输入信息量最多的优点,6维输入模式在准确性上更好,更加可靠,且9个隐层神经元时预测效果最佳。因此选择6维输入模式作为最终输入模式,选择隐层神经元数为9个。

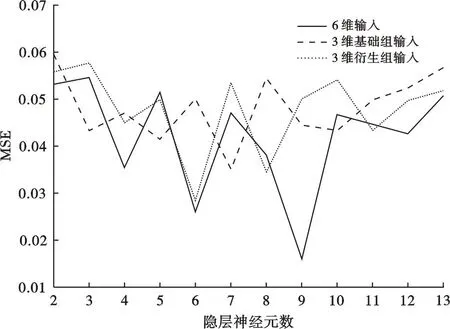
图5 输入维度对反演误差的影响

2.4 模型预测结果

由神经网络模型训练集、测试集与验证集结果(图6a、b)可以看出,训练集、测试集的均方误差分别为0.022 48、0.015 9。两个数据集的预测结果与实测值最大误差都不超过0.5 kPa,且训练集与测试集的相关系数R2分别为0.986 9、0.985 7,说明二者的真实值和预测值都非常接近,神经网络预测结果较为理想。为了检验神经网络模型预测效果,再将该网络应用于实验室测得的42个验证组数据进行预测,得到验证组的数据均方误差为0.0213 9,相关系数为0.987 4(图6c),表明训练数据的有限性对神经网络预测准确度的影响较小,该神经网络预测不排水抗剪强度结果可靠。

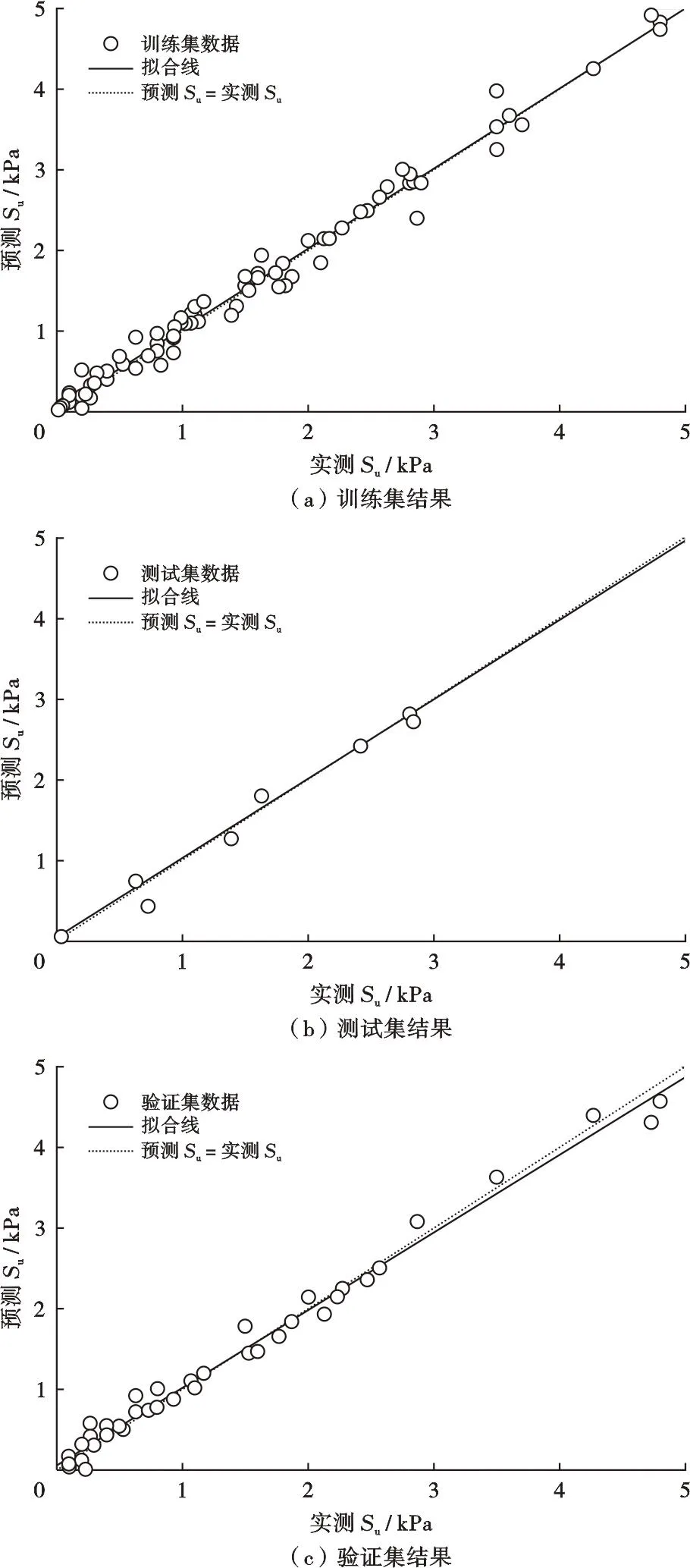
图6 训练集、测试集与验证集结果

综合训练集、测试集与验证集数据共132组,对模型预测误差进行分析:132组样本的不排水抗剪强度预测绝对误差都在0.5 kPa以内,其中50%的样本误差在0.1 kPa以内(图7),表明神经网络的预测精度能够满足实际工程需要。

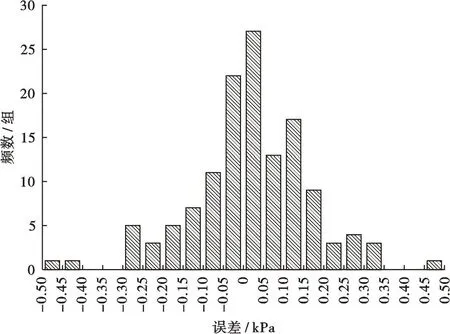
图7 真实值与神经网络模型预测值误差分布

为了对比研究神经网络模型和传统单物性指标关联的经验公式在预测超软黏土不排水抗剪强度方面的误差,按前人常用的指数函数、幂函数形式进行132组数据的拟合,选择相关系数更大者总结如式(9)～(11)。

Su=exp[(1.18-IL)/0.84],R2=0.795

(9)

Su=exp[(1.05-ILN)/0.119],R2=0.842

(10)

Su=exp[(1.1-WCR)/0.385],R2=0.762

(11)

由神经网络模型和不排水抗剪强度与液性指数、对数流动性指数、含水量比3种拟合公式(式(9)～(11))在预测不排水抗剪强度方面的相对误差累计比例分布(图8)可以看出,神经网络模型预测不排水抗剪强度的相对误差明显小于3种经验公式计算的相对误差。神经网络预测相对误差超过50%的样本占比仅11.8%,而经验公式计算的相对误差超过50%的样本占比高达55%左右。可见,基于含水率、液限、塑限、液性指数、对数流动性指数以及含水量比这6个物性指标,利用神经网络预测浅层软黏土的不排水抗剪强度具有较好的可行性和准确性。

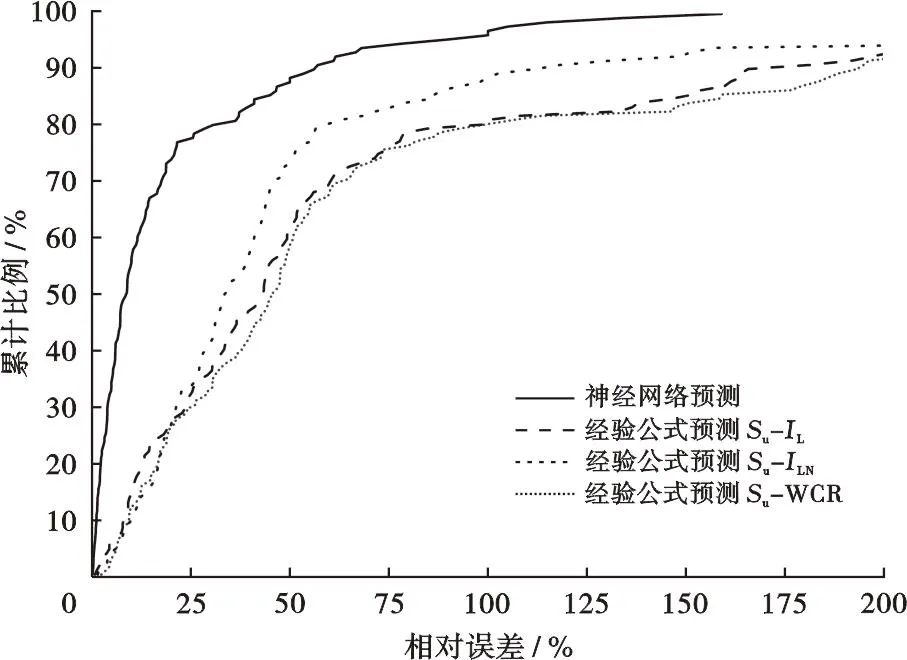
注:曲线数据点纵坐标代表小于横坐标所示相对误差的样本占总样本的比例。

为了进一步研究神经网络模型预测超软黏土不排水抗剪强度的区域适用性,在已有132组数据的基础上,先采用不包括某一地区的数据集进行训练和学习,再采用该地区的数据集进行测试。考虑到测试数据集的数据量需求,选择中国南海、美国波士顿以及日本德山3个区域进行超软黏土不排水抗剪强度的预测。多地区多种预测方法的预测均方误差对比(图9)表明,神经网络模型在排除该地区数据的情况下仍能较好地预测该地区超软黏土不排水抗剪强度,且其预测效果明显优于不排水抗剪强度与液性指数、对数流动性指数、含水量比这3个单一指标的拟合公式,说明神经网络模型能够较好地克服现有经验公式受地域限制的问题。神经网络模型对于中国南海区域超软黏土不排水抗剪强度预测误差相较美国波士顿和日本德山明显更大的原因在于中国南海的覆盖面积相较美国波士顿和日本德山要大很多,用一套数据代表整个南海的特征并不准确,这影响了神经网络的预测效果。

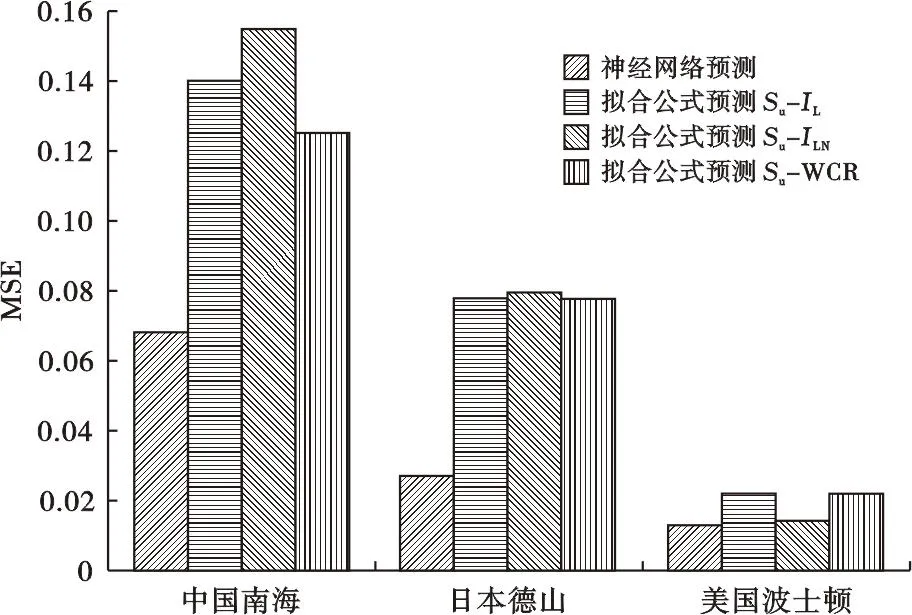
图9 神经网络和拟合公式预测不同地区Su的误差对比

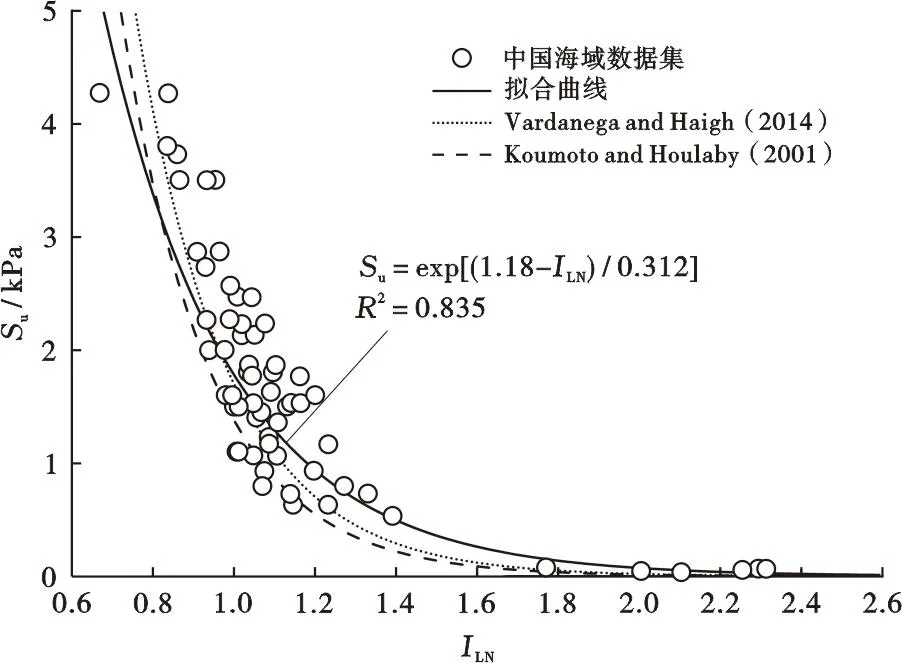
图10 基于中国海域数据的对数流动性指数与不排水抗剪强度经验关系

3 超软黏土物性指标敏感性分析及其经验公式

本文所建立的BP神经网络模型搭建了不排水抗剪强度与各物性指标之间的映射关系,可以根据该映射关系利用权积法求解各物性指标对不排水抗剪强度的敏感度系数。权积法以BP神经网络各层之间的连接权进行敏感度系数计算,计算第i个输入因子xi对第s个输出因子ys的敏感度系数sis的表达式[37]为

(12)

式(12)中:wij为输入因子xi与隐层神经元j的连接权,vjs为隐层神经元j与输出因子ys的连接权,f′(nets)与f′(netj)分别为隐层神经元j和输出神经元s的激活函数。

将训练与测试组数据90组和试验测得的42组数据合并,并进行数据归一化处理。将6个物性指标作为神经网络的输入神经元,不排水抗剪强度作为输出神经元,隐含层神经元数仍取9。从132组合并数据中随机选取122组数据作为训练集,另外10组数据作为测试集。为防止神经网络出现过拟合现象(即训练误差下降而测试误差上升),采用梯度下降法进行处理[38],使用训练集更新计算梯度、连接权和阈值,用测试集估计误差。一旦训练误差下降而测试误差上升,则停止模型训练,返回最终连接权和阈值,此时神经网络模型具有最小测试集误差,且物性指标与不排水抗剪强度之间的映射关系也已建立。最后,根据各物性指标与不排水抗剪强度之间的连接权值,根据式(12)计算得到各物性指标的敏感度系数(表5)。可以看出,在含水率(w)、液限(wl)、塑限(wp)、液性指数(IL)、对数流动性指数(ILN)以及含水量比(WCR)这6个物性指标中,对数流动性指数(ILN)的敏感度系数明显高于其他指标,说明该指标与不排水抗剪强度的相关性最强。该结论也与图8中的3种经验公式预测的误差曲线图相互验证,利用ILN与Su经验公式的估计误差小于其他2种公式。因此,若需要寻找与建立物性指标与不排水抗剪强度之间的经验关系,建议优先考虑对数流动性指数这一指标。

表5 物性指标敏感度

根据物质指标敏感性分析结果,利用本文中中国海域的89组数据建立对数流动性指数(ILN)和不排水抗剪强度Su之间的经验公式(13),其相关系数R2为0.835。该经验公式与现有经验公式具有相同的形式,也即基于对数流动性指数建立的不排水强度公式,可表示为式(14)的形式,其中,a、b为拟合参数。图12给出了不同经验公式针对中国海域数据集的结果,可以看出,当对数流动性指数(ILN)小于1.0时,中国海域经验公式的计算结果与Koumoto[10]的计算式(式(15))较为接近;大于1.0时,与Vardanega[9]的计算公式(式(16))较为接近,也再次表明现有经验公式均具有一定局限性。

Su=exp[(1.18-ILN)/0.312]

(13)

Su=exp[(a-ILN)/b]

(14)

Su=exp[(1.07-ILN)/0.217]

(15)

Su=exp[(1.12-ILN)/0.226]

(16)

4 结论

1) 在超软黏土不排水抗剪强度预测方面,当取样地点不同时,数据的离散性很大,现有经验公式存在受地域限制的问题,无法同时反应所有数据的变化特征,计算精度较低。

2) 考虑多因素影响的BP神经网络模型在超软黏土不排水抗剪切强度预测方面具有普遍适应性,该模型预测结果非常接近落锥试验实测结果,均方差低至0.0213 92,R2值达到0.987 4,且预测相对误差远低于现有经验公式计算的相对误差,预测效果明显优于现有经验公式。

3) 基于建立的神经网络模型,采用权积法计算得到对数流动性(ILN)指标对不排水抗剪强度(Su)最为敏感。据此建立以对数流动性指标为参数的中国海域超软黏土不排水抗剪强度预测经验公式,其相关系数R2为0.835,表明该公式在计算中国海域超软黏土不排水抗剪强度方面具有较好的精度,但由于数据量有限,依旧存在一定的局限性。