基于锥规划的配电网故障区段定位

蹇杭利, 李翠萍, 李江

(1.东北电力大学 电气工程学院,吉林 吉林 132012;2.上海电力大学 电气工程学院,上海 200090)

0 引 言

配电网连接输电网与电能用户,承担着分配电能的关键职能,是电力系统的重要组成环节,其运行可靠性与电能用户的生产、生活密切相关[1]。据有关数据表明,电网中发生的所有故障中,约80%到90%发生在配电网[2]。因此,配电网故障定位技术研究是保证配电网安全可靠运行的基础工作,对提高供电质量具有重要的现实意义。

随着配电网自动化以及通信技术的不断发展,微型同步相量量测单元(micro phasor measurement unit,μPMU)在配电网中逐渐普及[3]。文献[4]分析短路故障区段的电流相位差值,根据正序电流性相位突变值进行区段定位,无法对其他类型故障进行定位。文献[5]通过出故障前、后时间特征矩阵中元素的变化规律,实现配电网故障选线和精确定位、但该方法要求提取到明显的故障特征。综上,虽然在故障定位上的研究取得了一定的进展,但仍存在如下问题:①现阶段不可对所有节点进行配置μPMU;②以上算法均存在多解、区段定位可靠性不高问题;③故障区段定位算法速度慢,无法在线实时监测。

本文从配电网故障区段定位的需求出发,针对上述配电网故障区段定位面临的问题,提出基于锥规划的配电网故障区段定位算法。在Simulink中搭建仿真模型,结果表明该算法定位速度快,不受故障类型、故障位置的影响,可以准确定位故障区段。

1 配电网拓扑结构分析

某一个区段发生短路故障后,故障附近区段电流值的突变,是故障区域的主要特征。对于基态下的区段-量测关联矩阵B。若从变电站到第Mi个微型同步量测单元(负荷支路)的路径中包含了第i个区段,则bij=1;否则bij=0。μPMU进行量测后,对获取的三相电流进行克拉克变换[6]如下:

(1)

(2)

(3)

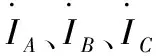
构建克拉克电流模值和Isum并构建克拉克相角θsum。

Isum=Iα+Iβ

(4)

θsum=θα+θβ

(5)

通过对每一个量测节点的Isum进行比较,获取所有量测节点中最大的Isum-m,并将各个量测值与最大量测值做比值,构建克拉克电流幅值状态指标矩阵IK-I。

Isum-max=max(Isum-1,Isum-2,…,Isum-Nmea)

(6)

(7)

IK-I中的数值最大为1,当其中某个元素接近于1时,表示该部分距动作行为越近,影响较大;反之则影响较小,或者正常运行。求取所有量测节点的θsum的均值,建立克拉克电流相角状态指标矩阵IK-θ。

(8)

(9)

IK-θ中的数值越大,表示该部分距动作行为越近,影响较大;反之则影响较小,或者正常运行。根据IK-θ和IK-I建立克拉克电流状态指标矩阵IK。

IK=IK-I+IK-θ

(10)

在IK中,某一个元素的值越大,则离故障区段越近。基态下配电网的量测节点与区段之间的拓扑结构用B表示,故障情况下,用IK表征故障信息。为了更好地表征每一个区段的状态信息,将B和IK进行综合考量,建立电流-量测关联矩阵KB。

(11)

由于量测节点有限,完全依靠KB进行故障区段的确定可能存在多解或者误解,为提升故障区段的定位准确性,采用锥规划算法进行故障区段的精确定位。

2 基于锥规划的区段定位算法

2.1 锥规划模型的建立

本文依托基尔霍夫电流定律建立网络方程,在构建的IK基础下,以克拉克电流指标值与下一级克拉克电流指标差值之和最小作为目标,得到如下目标函数。

(12)

式中:Ik-z为配电网中克拉克电流指标值与下一级克拉克电流指标差值之和;Tp为该周期内所有时段总数量;t为时间段;IK-n为第N个配置量测单元的节点的克拉克电流状态指标值;Nsub-mea为第N个量测单元的下一级量测单元的总数量;Hn为与第N个量测单元相连接的下一级量测单元M的集合,Hn={1,2,…,Nsub-mea};xa,b为目标函数的整行约束;IK-n,set(t)为下一级量测单元的克拉克电流指标差值之和。经矩阵形式的转换,目标函数化简为:

IK-subX=Ik-z

(13)

式中:IK-sub为第N个量测单元的下级克拉克电流指标差值矩阵;Ik-z为所有量测单元对应的克拉克电流指标差值矩阵;X为整数约束矩阵。基于上述目标函数和约束条件,可以建立标准的锥规划模型。标准的锥规划形式为:

(14)

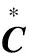
2.2 二阶锥算法求解

(15)

(16)

式中:Xj为解的子集;B为对称矩阵;k为子集的个数。由于现阶段配电网中的所有节点若均配置同步量测单元,则成本过高,不符合实际场景,因此假设支路节点均为配置同步量测单元,则X对应的支路元素则为0,减少了解空间的维数。对于减少维数的线性问题,采用内点法即可求取最优解了。实质为将以克拉克电流指标值与下一级克拉克电流指标差值之和最小作为目标,将其转变为锥规划模型,进行最优化求解,若差值越小,则越接近故障区段。故障区段定位流程如图1所示。

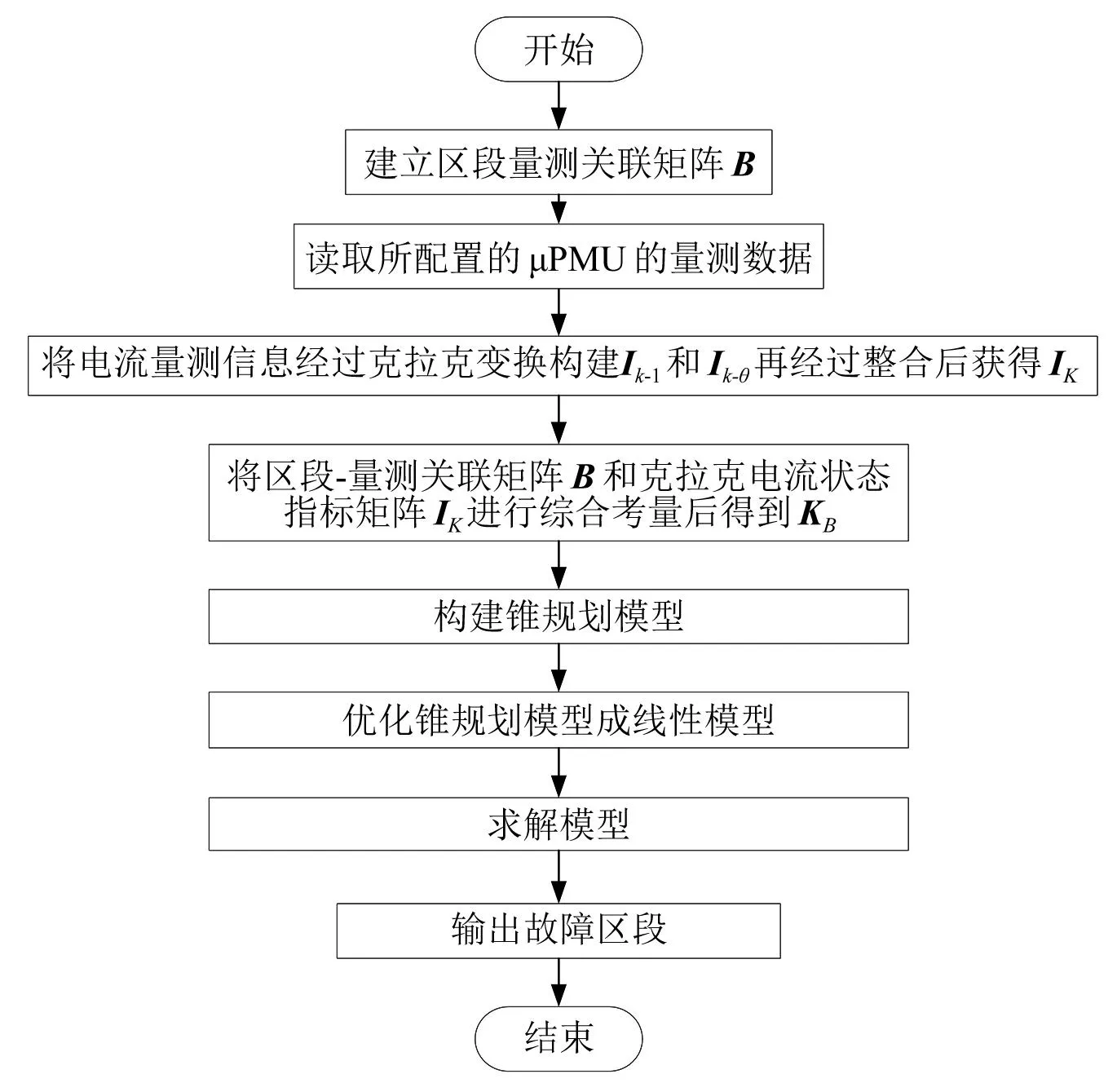
图1 配电网区段定位算法流程图

3 算例分析

为验证所提出的算法在大规模配电网的适用性,使用Simulink,以图2所示的IEEE 33节点系统为例进行仿真测试。对于μPMU的配置,本算例引用文献[7]已优化后的配置算法进行最佳配置。如图2所示,白色标记的节点为配置了μPMU的节点,黑色标记的节点为未配置测量单元的节点。

图2 IEEE 33节点系统拓扑结构

在IEEE 33节点的基础上分别设置单相接地、两相短路,三相接地故障(μPMU数据无畸变、无丢失)验证算法的有效性和准确性。为了考虑DG的投入与切断对算法的影响,用[K1,K2,K3)〗分别表示DG1,DG2,DG3的状况,如果DG接入到配电网中,K值则为1;切除则为0。算法有效性验证如表1所示。

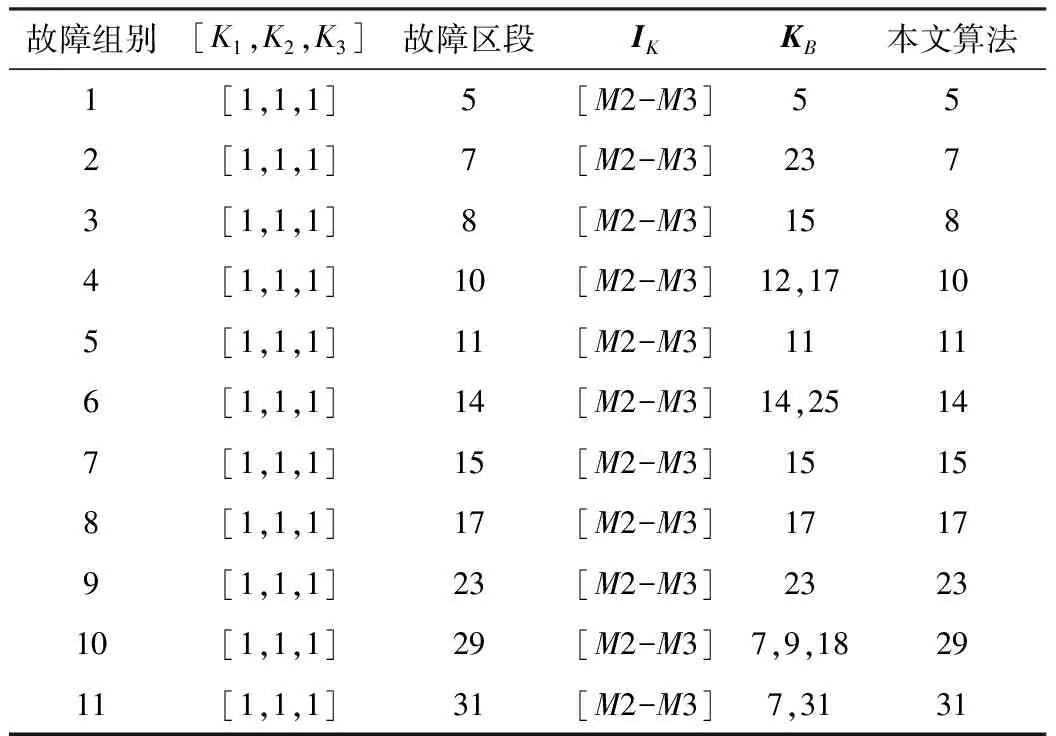
表1 算法有效性验证

表1中一共有10组故障组别,分别在随机的DG状态下进行不同故障测试。首先使用IK进行故障区段的判断,只可以进行一个大的区段的定位。若使用KB进行故障区段的定位,容易出现定位错乱的情况。通过锥规划模型的建立并求解可获得准确故障区段。为验证算法的性能,分别使用本文算法、多端故障电流匹配的算法[8]、克拉克电流相角差值定位算法和基于IELM算法的定位算法[9]。表2为采用三种算法的对比。

表2 算法对比

通过将上述三种算法和本文算法进行同种故障的测试分析,从而得出对比性。其测试结果如图3和图4所示。

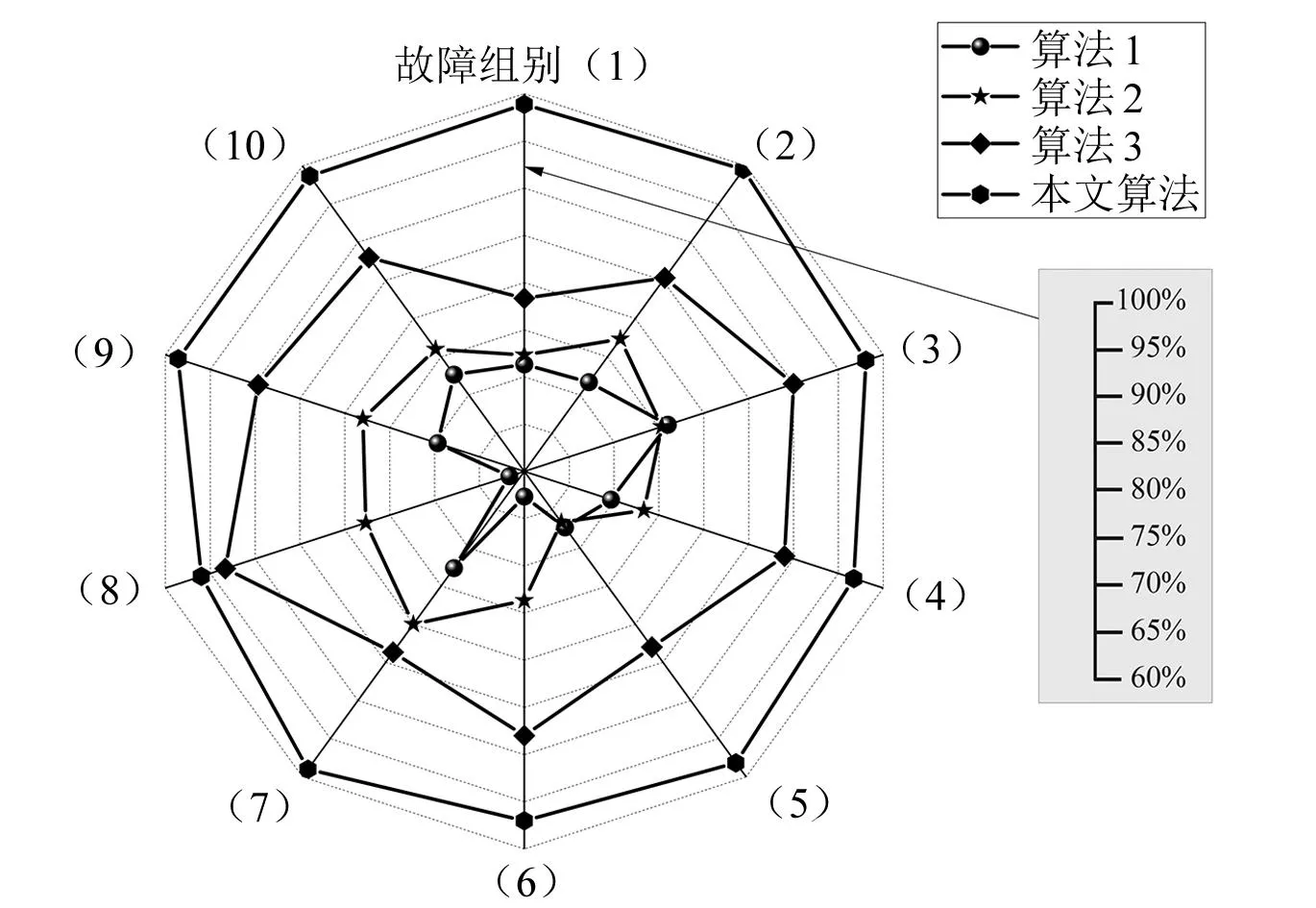
图3 算法平均准确率

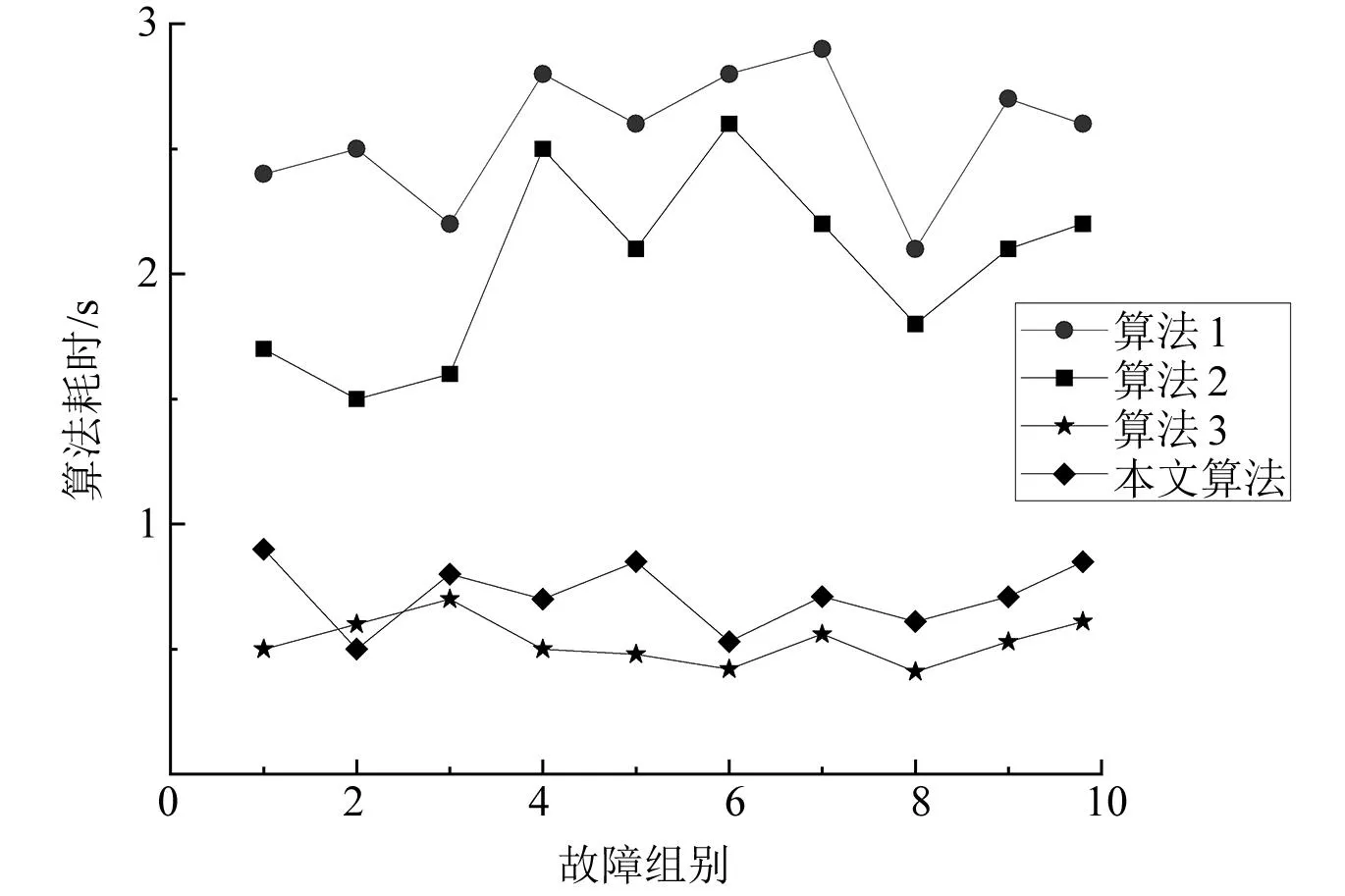
图4 算法耗时对比

由图3可知,算法的准确性顺序都大致为:本文算法>IELM算法>克拉克电流相角差值算法>多端故障电流匹配算法。由图4可知,算法平均耗时:IELM算法>本文算法>克拉克电流相角差值算法>多端故障电流匹配算法,但是本文算法和IELM算法的相差时间不大。所提算法在算法2的基础上,解决了全节点覆盖量测装置的痛点,同时采用锥规划算法提高了最优解的求解,提高了准确性和算法速度。

4 结束语

本文以配电网为研究对象,以简单辐射状单电源配电网为例,采用锥规划算法进行优化求解,提出了一种基于锥规划的配电网故障区段定位算法,具有以下特点。

(1) 本文在非所有节点都配置量测装置的前提下,考虑了量测装置与配电网整体的关联,保证系统的区段均完全可观。

(2) 在基本算法上,以克拉克电流指标值与下一级克拉克电流指标差值之和最小作为目标构建锥规划模型,优化标准锥规划模型,实现对故障区段的准确定位。

(3) 在Simulink中搭建了IEEE 33节点配电网模型,在多个算例中进行了仿真验证。结果表明,在量测装置上传数据不畸变的情况下,本文算法不仅可以应用于短路、断路等各种类型的故障,同时还不受多种类型分布式电源接入与切除影响。

未来将针对在μPMU上传信息畸变的情况下,研究如何将故障区段多解问题转变为锥规划模型,进而求得故障区段的最有解,从而可为提高新型电力系统的稳健性而提供技术支撑。