渗流条件下富水砂层盾构隧道开挖面临界支护压力计算分析*
张跃明 钟久强 余 金 涂万年 朱碧堂,5
(1.广州地铁设计研究院股份有限公司,510010,广州; 2.浙江省交通规划设计研究院有限公司,310031,杭州;3.江西水利职业学院建筑工程系,330013,南昌; 4.华东交通大学土木建筑学院,330013,南昌;5.江西省地下空间技术开发工程研究中心,330013,南昌)
0 引言
临江依河的城市地铁盾构隧道往往需要穿越富水砂层,在土舱内外水压差作用下,不可避免地会发生渗流现象。富水砂层由于黏性低、自稳能力差,在渗流作用下,盾构掘进容易引起土体沉降变形和开挖面失稳破坏。对于土压平衡盾构,盾构推力通过土舱内改良的渣土均匀传递至开挖面以维持土压平衡。开挖面压力的准确计算对控制隧道开挖引起的土层损失、土体变形及地层稳定至关重要。
由于传统平衡法无法准确考虑土体本构模型、尺寸及边界效应的影响,许多学者采用有限元数值模拟进行研究分析。文献[1]采用Plaxis 3D有限元软件,基于M-C(摩尔-库伦)本构模型,通过不同内摩擦角及埋深比的变化,研究了不排水条件下砂土中盾构隧道开挖面临界支护力的变化情况,并提出了计算开挖面临界支护压力的简化方法。文献[2]利用Midas-GTS软件建立了多层摩擦型材料的三维滑移破坏模型。
目前,已有的确定开挖面临界支护压力的方法较少考虑开挖面发生渗流的情况。文献[3]基于二维稳态渗流模型,提出了考虑渗流影响下的开挖面临界支护压力计算式。文献[4]采用Plaxis 2D软件,分析了考虑流固耦合效应影响下,隧道开挖面附近土体位移及极限支护力的变化情况,研究了埋深比对开挖面极限支护压力、地面最大沉降值及土拱效应的影响。
总体而言,现有针对发生渗流情况下的临界支护压力计算无法反映盾构隧道开挖面的三维效应。由于缺乏理论支撑,所施加的开挖面压力往往无法满足开挖面稳定或地面沉降变形的控制要求,导致工程险情时有发生。因此,对发生渗流条件下的盾构隧道开挖面失稳破坏模式开展三维数值模拟分析,研究渗流对开挖面临界支护压力的影响,对隧道开挖稳定、控制隧道开挖引起的土体变形及其对周边建(构)筑物的影响具有重要的意义。
针对不发生渗流条件下的盾构隧道开挖面,本文采用Optum G3软件开展三维有限元上下限极限分析,明确开挖面临界支护压力近似理论解和失稳破坏模式,并基于敏感性分析,提出不发生渗流条件下的开挖面临界支护压力计算式。对于开挖面发生渗流的情况,本文采用Plaxis 3D软件开展三维有限元分析,明确开挖面失稳破坏模式,并基于开挖面支护力-位移曲线确定开挖面的临界支护压力。在主要参数敏感性分析的基础上,综合考虑无渗流条件下的开挖面临界支护压力计算式,进一步提出了考虑稳态渗流条件下的临界开挖面压力计算方法。
1 无渗流条件下开挖面临界支护压力
1.1 Optum G3三维极限分析模型
采用有限单元极限分析法和Optum G3商业软件计算分析开挖面的稳定性。Optum G3是一款基于关联流动法则(即土体剪胀角与内摩擦角相同)的三维有限元极限分析软件,可给出与上下限解非常接近的近似理论解。需要输入的土体参数包括内摩擦角φ、黏聚力c、剪胀角Ψ、弹性模量E、静止土压力系数K0、重度γ、泊松比ν等。值得说明的是,剪胀角对开挖面临界支护压力的影响不大[5],不影响本文的分析计算结果。
针对均质砂土,建立Optum G3三维极限分析模型,如图1 a)所示。本文取隧道直径D=6 m,砂土破坏服从M-C屈服准则,黏聚力c=0,土体重度γ=18 kN/m3,φ=20°~40°。由于盾构隧道存在对称性,为了提高模型的计算效率,以隧道中轴线为对称轴,取半边模型进行研究,模型的相对尺寸如图1 b)所示。模型上表面设置为自由面,下表面限制水平及竖向位移,侧面限制水平位移。
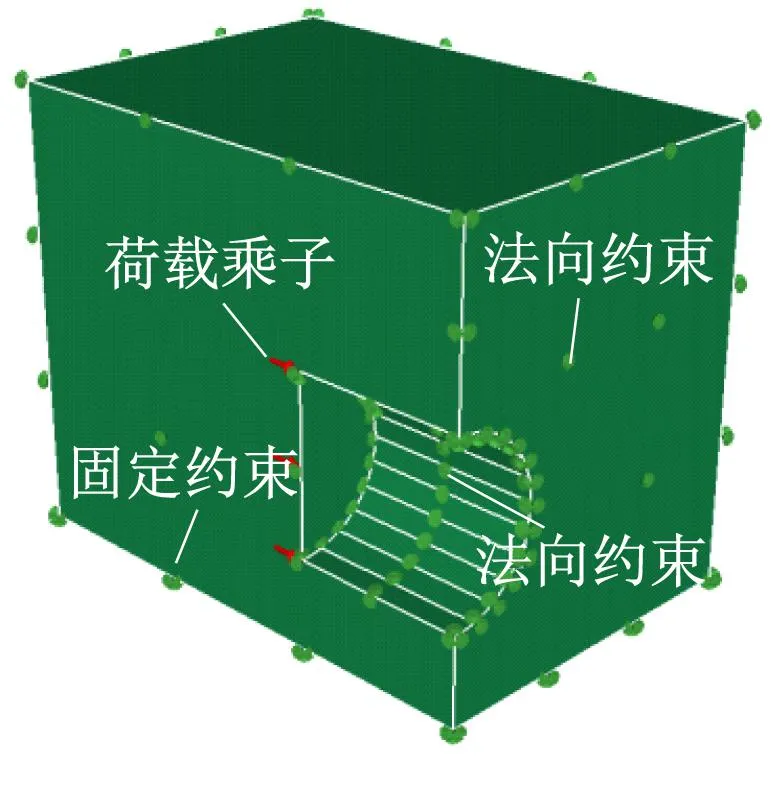
a) 三维模型
为消除初始边界影响、加快计算速度,在开挖模拟过程中,假定一次性开挖土体至6 m位置,对隧道四周侧壁施加径向约束,以模拟衬砌限制其径向位移。在开挖面上施加朝向隧道内部(垂直于开挖面)的一个初始荷载和荷载乘子,通过搜索计算得到极限状态时的荷载乘子,即可获得开挖面临界支护压力。采用自适应4节点四面体单元进行网格划分,前一次计算结束后对可能的塑性区重新进行网格加密划分,以提高计算精度,模型一般迭代3次即可达到稳定值。在计算过程中,采用上下限极限分析混合求解器,可获得开挖面临界支护压力的近似理论解。
1.2 无渗流条件下开挖面破坏模式
当埋深比C/D=1.0且φ=25°、30°、35°、40°时,开挖面失稳破坏模式如图2所示,破坏区域近似为图中虚线和隧道开挖面包围的区域。当φ=25°时,开挖面破坏从开挖面底部发展至接近地面区域;当φ>25°时,开挖面滑移破坏区局限于开挖面前方一定的范围内,这与文献[6]中的砂土开挖面破坏模式一致。对于一般的砂土地层(φ≥30°),只要开挖面压力大于临界支护压力,在C/D>1.0情况下,开挖面前方区域在短时间内不会发生大面积破坏。
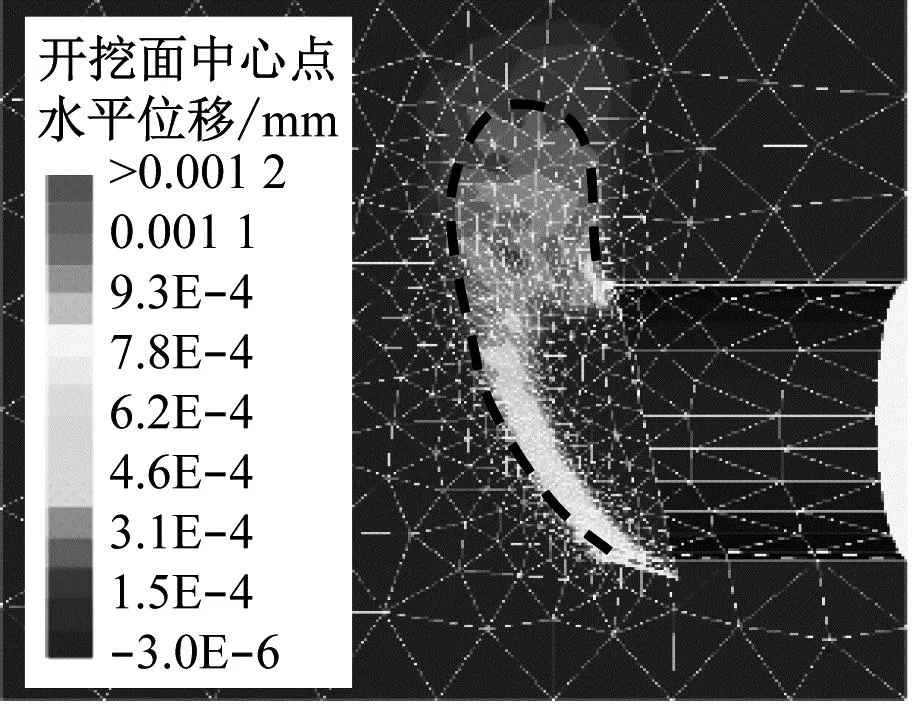
a) φ=25°
当φ=30°且C/D=0.5、1.0、2.0、4.0时,开挖面失稳破坏模式如图3所示。除C/D=0.5时,开挖面滑裂面向上延伸几乎贯通至地面外,其余开挖面前方土体失稳区域范围基本一致,均为自拱底向上超出拱顶一定的高度,失稳面形态均为狭窄的“灯泡状”圆形滑弧,且由于土拱效应,滑裂面不再延伸至地面。由此可知,浅埋盾构隧道掘进时,开挖面的支护压力不足,容易引起地面塌陷破坏;对于深层盾构隧道掘进时,当开挖面压力偏小时,地面主要表现为过量沉降。
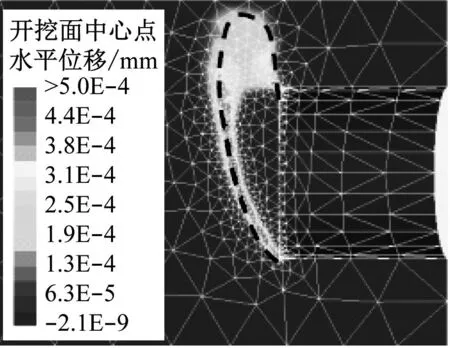
a) C/D=0.5
1.3 无渗流条件下开挖面临界支护力简化计算
文献[1]中提出的不排水情况下,均质土中隧道开挖面临界支护压力可以表示为:
(1)
式中:
pf——开挖面临界支护压力;
Nc——黏聚力承载系数;
q——地面荷载;
c′——土体有效黏聚力;
Nq——超载承载系数;
Nγ——土体重度承载系数。
文献[1]的研究结果表明,当φ≥20°、C/D≥1.0时,地面超载对开挖面临界支护压力没有影响,这与前述滑裂面发生位置和大小不一致。因此,对于富水砂层(黏聚力为0),经整理,式(2)可简化为求解土体重度承载系数的形式:
Nγ=pf/γD
(2)
根据前文所述Optum G3计算结果,掌子面量纲一化极限支护压力(即Nγ)与砂土内摩擦角正弦值sinφ之间的关系曲线如图4所示。由图4可知:当φ=20°~40°时,随着内摩擦角正弦值sinφ的增大,pf/γD逐渐降低。两者可采用式(3)进行拟合,则有:
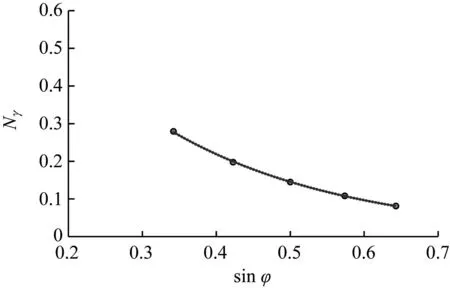
图4 量纲一化后的Nγ与sin φ关系曲线
pf=NγγD=1.12e-4.09sin φγD
(3)
对于φ为20°和40°时的情况,将Optum G3计算结果与式(3)的计算结果进行对比发现,两者的最大误差不超过5%。由此可知,式(3)可用于不考虑渗流条件下的开挖面临界支护压力的简化计算。
2 Plaxis 3D流固耦合分析模型
上述均质砂土地层开挖面临界支护压力计算没有考虑开挖面处的地下水渗流,即默认假定土舱内水头与地层中的地下水头相等,不发生渗流。此时,开挖面的总支护压力为由式(3)计算所得的开挖面临界支护压力与地下水压力之和,导致深埋隧道所需总压力高于人工作业极限压力350 kPa。此外,在盾构隧道开舱换刀时,需要考虑渗流条件下的最小开挖面支护压力。
2.1 计算模型
考虑到Optum G3没有渗流模块,本文采用Plaxis 3D有限元分析软件通过稳态渗流与流固耦合分析,研究渗流力和内外水头差对开挖面失稳模式和临界支护力的影响。
鉴于盾构隧道的对称性,以隧道中轴线为对称轴,取半边模型进行研究,以提高计算效率。Plaxis 3D隧道开挖有限元模型如图5所示。对于位移边界条件,模型上表面设置为自由面,下表面限制水平及竖向位移,侧面限制水平位移。对于渗流边界条件,模型上表面设置为排水面,隧道剖面所在侧面及下表面设置为不排水面,其余侧面设置为排水面;隧道开挖面设置为无压自由渗流,侧壁为不排水面。
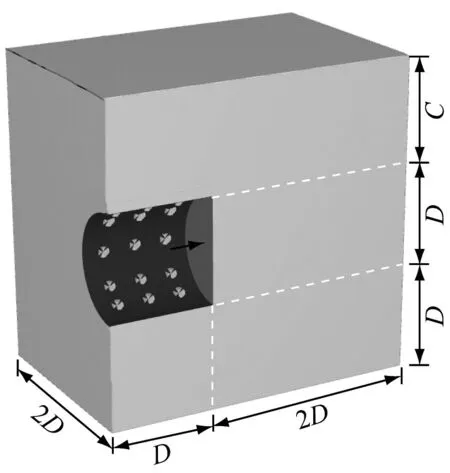
a) 相对尺寸关系
假定土体为均质砂土,土体破坏服从M-C屈服准则,c=0,γ=18 kN/m3,φ=20°~40°,渗透系数为60 m/d。网格划分采用自适应10节点四面体单元,单元数量共计23 189个。施工步阶段分为初始地应力平衡与稳态渗流计算。开挖面处施加法向垂直支护压力,初始施加值大小为静止水土压力,然后逐步递减,直至开挖面失稳得到最小支护压力。
2.2 下限支护力临界值的确定
采用力-位移法[1,5]确定隧道开挖面临界支护压力,主要步骤如下:
1) 取隧道开挖面中心点为位移控制点,于地应力平衡初始施工步后创建分阶段渗流分析步;
2) 激活隧道侧壁位移边界与渗流边界,激活开挖面处渗流边界;
3) 施加初始开挖面支护力,其值大小为静止水土压力,激活计算步;
4) 紧跟初始分析步创建多个并列渗流分析步,开挖面支护力以10 kPa递减,其余条件不变;
5) 当计算不收敛后,将最后一级收敛开挖面压力按1 kPa逐渐降低,直至开挖面失稳破坏,Plaxis 3D模型无法收敛,对应的开挖面压力可视为临界开挖面压力。当支护力发生微小改变而位移发生突变时,判断该点为失稳点,此时对应的支护力值即为下限支护力临界值。
3 模拟计算结果分析
3.1 稳态渗流模式
当C/D=1.0时,渗流场孔压分布如图6 a)所示。模型整体渗流场孔压分布呈T字形,开挖面上方的水压/水位显著降低,有效应力有所增长,进而引起开挖面上方的土体发生沉降。由于开挖面为无压自由渗流面,故在开挖面处孔压为0。开挖面处的渗流矢量分布如图6 b)所示。由如图6 b)可知:拱顶处渗流流量较小,拱底处渗流流量较大。

a) 孔压分布
不同C/D值产生的孔压分布和渗流模式相似,但由于C/D不同,则自由水面下降的幅度有所不同,进而导致开挖面周边和上方有不同的水头等高线。不同C/D条件下,开挖面周边水头等高线示意图如图7所示。其中,A线范围的区域为开挖面渗流主要影响区,大约前方1.5D范围内存在明显的渗流水位下降,容易发生土体失稳破坏。
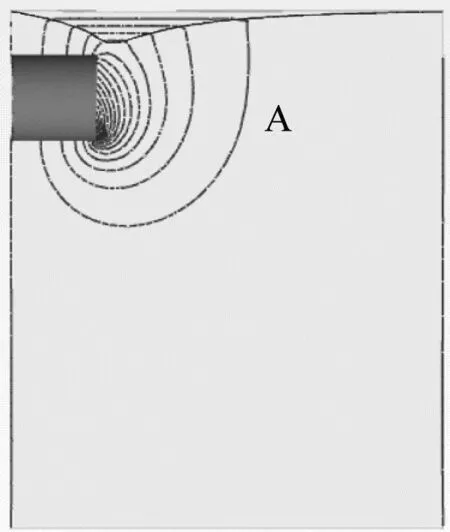
a) C/D=0.5
3.2 流固耦合作用下的开挖面失稳模式
当C/D=1.0且φ=25°、30°、35°、40°时,开挖面失稳破坏模式如图8所示。考虑渗流条件下的开挖面失稳破坏模式与未考虑渗流条件下的失稳破坏模式(见图2)相似,但破坏区域相对较大。当φ=25°时,开挖面破坏从开挖面底部发展至地面;当φ>25°时,开挖面滑移破坏区局限于开挖面前方一定的范围内。在极限状态下,开挖面上方土体出现了较大的沉降。
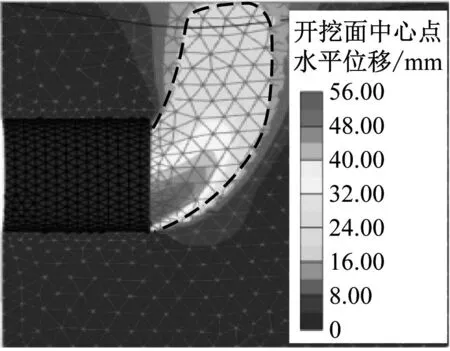
a) φ=25°
3.3 渗流条件下的开挖面临界支护压力
当C/D=1.0时,稳态渗流条件下,本文由Plaxis 3D软件分析所获得的开挖面最小支护压力同文献[5]及文献[7]的数值计算结果较接近,位于上下限极限分析结果之间,验证了本文所提计算方法获得的下限支护力临界值是合理的。
考虑地下水不同状态对开挖面临界支护压力的影响,当C/D=1.0时,干砂、未发生渗流条件下及发生稳态渗流条件下,饱和砂土临界支护压力与开挖面中心点水平向位移关系曲线如图9所示。三种情况下的临界支护压力值分别为11 kPa、43 kPa及100 kPa,相应的静止水土压力值为128 kPa。因此,当考虑地下水稳态渗流时,开挖面所需的临界支护压力远远大于干砂地层,约为干砂地层的4倍。由此可见,渗流可显著降低掌子面稳定所需要的最小临界支护力,这是因为渗流释放了孔隙水压。

图9 不同地下水状态下的饱和砂土临界支护压力与开挖面中心点水平向位移关系曲线(C/D=1.0)
3.4 内外水头差对开挖面临界支护压力的影响
当C/D=1.0时,不同水头差条件下,临界支护压力与开挖面中心点水平向位移关系曲线(D=6 m,渗透系数为60 m/d)如图10所示,其中h1为土舱内外地下水头差。随着h1的不断减小,曲线拐点对应的临界支护压力也逐渐变小。当水位线位于隧道中轴线以上时,其支护压力降幅明显大于位于中轴线以下的支护压力降幅。
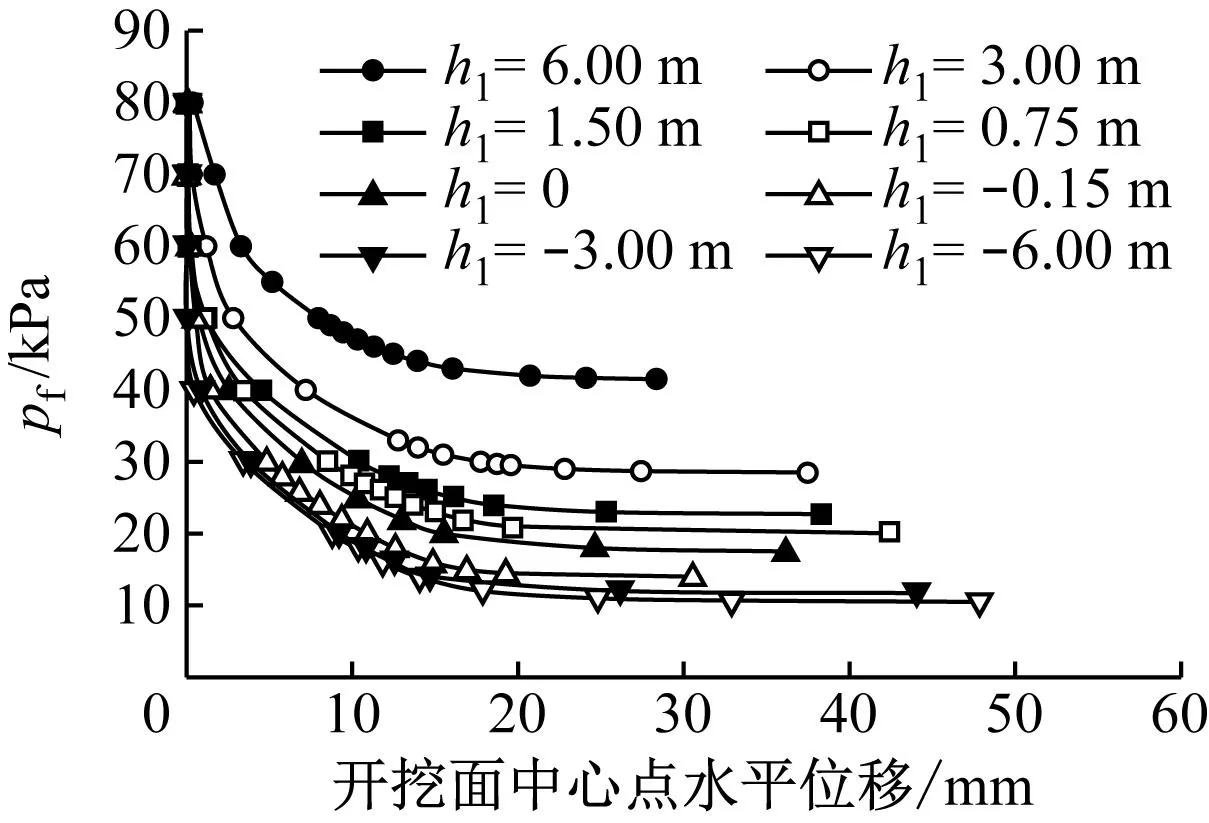
图10 不同水头差条件下临界支护压力与开挖面中心点水平向位移关系曲线
基于上述水头差和内摩擦角敏感性分析,考虑稳态渗流条件下的富水砂层开挖面临界支护压力可以表示为:
pf=F0γ′D+F1γwD=
1.12e-4.09sin φγ′D+F1γwD
(4)
式中:
F0——重度修正系数;
F1——黏聚力修正系数;
γw——水的重度;
γ′——土体浮重度。
式(4)第一项为无渗流条件下砂土稳定需要的开挖面临界支护压力;第二项为土舱与地层内外水头差作用下需要的额外支护压力,用于抵挡渗透力。通过埋深比、内摩擦角和水头差等参数敏感性分析,可拟合得到:
(5)
式中:
hw——地下水位深度。
则富水砂层开挖面临界支护压力可以表示为:
pf=1.12e-4.09sin φγ′D+
(6)
Plaxis 3D数值计算与式(6)计算所得的开挖面临界支护压力对比如图11所示。两种方法所得的开挖面临界支护压力误差在5%以内。由此可知,式(6)可更为简便地确定发生稳态渗流条件下的开挖面临界支护压力。
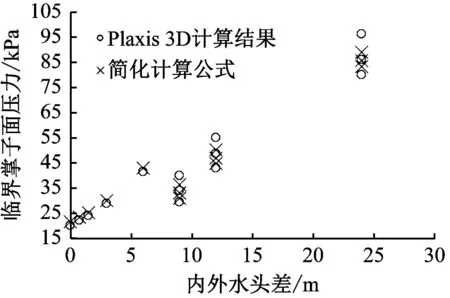
图11 Plaxis 3D数值计算与式(6)计算所得的开挖面临界支护压力对比
4 结语
通过Optum G3三维上下限极限分析和Plaxis 3D有限元数值模拟分析,分别明确了无渗流条件和发生渗流条件下的开挖面破坏模式。通过主要参数的敏感性分析,提出了计算全断面砂层的临界开挖面支护压力计算公式。主要获得以下结论:
1) 当C/D<1.0、φ≤25°时,开挖面破坏区从拱底发展至接近地面,容易发生浅层隧道冒顶破坏。当C/D≥1.0、φ>25°时,开挖面前方失稳破坏区局限于开挖面上方一定范围内,发生渗流时比无渗流时的破坏区域稍大。
2) 在开挖面无渗流情况下,富水砂土地层盾构隧道开挖面的临界支护土压力可采用pf=1.12e-4.09sin φγD计算式进行计算,此外该计算值还需加上地下静止水土压力。
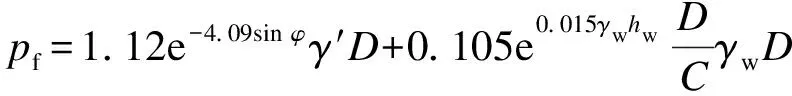
4) 对于不同的地下水状态,临界开挖面支护压力排序为:未发生渗流的临界开挖面支护压力>发生渗流的临界开挖面支护压力>干砂条件下的开挖面临界压力。

