基于人工势场引力因子的机械臂避障规划算法
苗田恬,方厚招,安 康,孙延博,方祖华,管西强+
(1.上海师范大学 信息与机电工程学院,上海 201418;2.中国航天科技集团有限公司 上海航天技术研究院 上海卫星工程研究所,上海 201108)
0 引 言
机器人技术的发展已经成为国家科学技术发展水平和工业自动化程度[1]的重要衡量指标之一。其中,像人一样的机械臂能够高效协助人们完成加工、搬运、整理等繁琐的工作任务,减少、简化冗杂的体力劳动[2]。比如KUKA公司的iiwa[3]、Kinova公司的Jaco[4]、FANUC公司的M-430iA[5]、国内JAKA公司的Ai3[6]等机械臂的宜人化、灵巧化,让生活、工作、娱乐变得越来越智能。因此,提高机械臂的安全性、可靠性,合理的路径规划与实时避障必不可少。机械臂避障路径规划的典型方法有遗传算法[7]、模糊逻辑控制算法、栅格法、人工势场法[8,9]、RRT[10]、PRM等。
针对人工势场法存在的目标不可达和局部极小值[11]问题,国内外众多学者对人工势场法进行了不同程度的研究和优化。张大志等[12]提出一种基于水流场改进的人工势场方法,解决了传统人工势场法中的局部极小值、路径振荡以及目标不可达等问题,但是在进行动态避障时,移动机器人需要从动态障碍物前方绕过,会造成增加避障路程和避障失效概率的问题。J. Lee等[13]对附加的防碰撞条件进行了改进,并引入改进算法,克服对称对齐的用户-障碍-目标问题。M.H. Mabrouk等[14]用一阶微分方程表示移动机器人的内部状态,并添加函数使之克服局部极小值,向目标位置移动。但两者均未考虑位置定位精度问题,即使通过人工势场法或其变型产生一个完美的目标路径,当路径上的位置精度不足时,移动机器人可能会经历不必要的振荡运动或意外碰撞。S. D. Das等[15]研究了人工势场在机器人三维运动规划中的应用,然而,它的应用仅限于仅包含点障碍物,以及忽略末端效应器方向的场景。
1 人工势场模型
1.1 人工势场算法
人工势场算法示意如图1所示,Xo表示障碍物的中心位置,圆形阴影区域代表障碍物范围,星号中心位置Xg表示目标点位置,圆形Xt(x,y) 代表机械臂末端位置。机械臂末端在运动的过程中由于同时受到障碍物斥力Fatt和目标点引力Frep的作用,最终在其合力的作用下成功避开障碍物并停止在目标点位置。
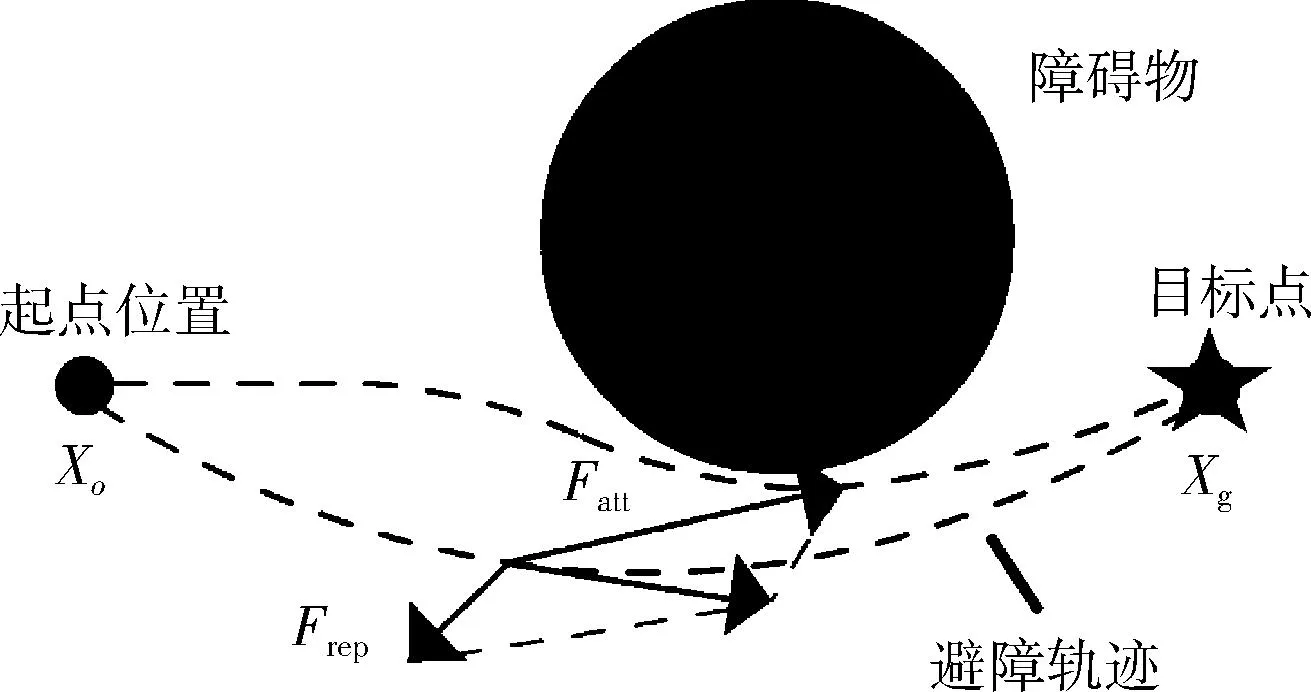
图1 人工势场算法
其中目标点对机械臂产生的引力势场表示为
(1)
其中,ka为引力势场系数;l(Xt,Xg) 表示一个矢量,其大小为目标点中心位置Xg(x,y) 到机械臂末端位置Xt(x,y) 的距离 |Xt(x,y)-Xg(x,y)|, 方向由机械臂末端指向目标,Xt(x,y) 越大,对应的引力势场Uatt越大。
机械臂受到的障碍物斥力势场表示为
(2)
其中,kb为斥力势场系数;ρ0为常数,表示障碍物产生的斥力势场的最大范围;l(Xt,Xo) 表示一个矢量,为障碍物中心位置Xo(x,y) 到机械臂末端位置Xt(x,y) 的距离 |Xo(x,y)-Xg(x,y)|, 方向由障碍物指向机械臂末端,距离矢量l(Xt,Xo) 越大,对应的斥力势场Urep越小。
目标点中心位置Xg(x,y) 和障碍物中心位置Xo(x,y) 固定,在式(1)中引力势场表达式的引力势场系数ka为给定的值,其值的合适取值则会影响到引力的大小,直接影响到机械臂末端的运动路径。同理,在式(2)斥力势场表达式中,斥力势场系数kb和斥力势场作用范围常数ρ0的确定影响到斥力的大小。研究模型参数如何设定能够使得机械臂末端获取最短避障路径是本文的重点。因此,本文将充分分析引力势场系数ka、 斥力势场系数kb以及斥力势场作用范围常数ρ0这3个参数对机械臂末端运动路径的影响。
1.2 斥力势场作用范围常数ρ0分析
研究斥力势场作用范围常数ρ0变化对机械臂末端路径的影响,定义机械臂起点与目标点的连线为L, 障碍物中心位置到该连线的垂直距离为Lf。 结合斥力势场公式(式(2)),可做以下分析(如图2所示,假设障碍物与目标点距离为0.5,Lf=0.4):
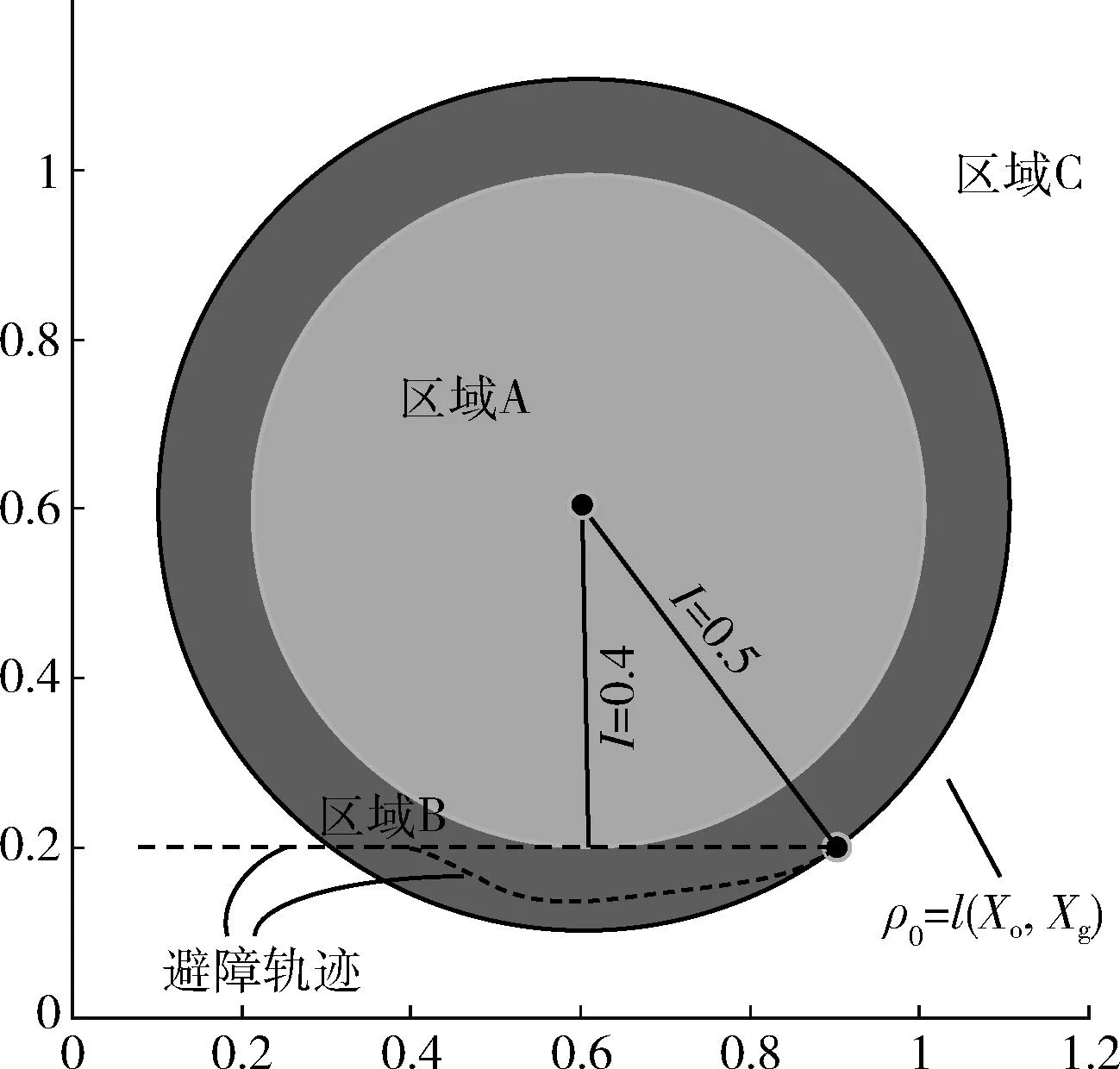
图2 以ρ0为半径的斥力范围作用区域
(1)当调节斥力势场作用范围常数ρ0值小于障碍物中心位置到连线L的垂直距离Lf, 即ρ0处于区域A(ρ0<0.4) 时,满足l(Xt,Xo)≥ρ0条件,障碍物对机械臂末端斥力为零,机械臂仅受到引力的影响,机械臂末端路径为直线。
(2)当调节斥力势场作用范围常数ρ0值大于障碍物中心位置到连线L的垂直距离Lf, 小于障碍物与目标点距离,即ρ0处于区域B(0.4<ρ0<0.5) 时,机械臂末端受到障碍物的斥力,运动过程中将呈现出远离障碍物的现象。
(3)当调节斥力势场作用范围常数ρ0值等于障碍物中心位置与目标点距离(即ρ0=0.5), 机械臂末端在运动的过程中不仅远离障碍物,且在达到目标点时所受斥力为零,与情况(2)相比,该情况的轨迹更加平滑,机械臂末端最终以平滑路径轨迹停止在目标点位置。
(4)当调节斥力势场作用范围常数ρ0值大于障碍物中心位置与目标点距离,即ρ0处于区域C(ρ0>0.5) 时,当机械臂末端到达目标点附近时仍受到斥力作用,使得机械臂末端最终无法到达目标点位置。
以ρ0为半径的斥力范围作用区域如图2所示。
综上分析,斥力势场作用范围常数ρ0等于障碍物位置与目标点位置距离时,机械臂末端在运动过程中拥有较为平滑的轨迹并成功到达目标点。因此,本文选取ρ0等于障碍物位置与目标点位置距离对机械臂末端路径进行后续分析。
1.3 引力势场系数与斥力势场系数比值 (ka/kb) 分析
由式(1)和式(2)得到引力势场和斥力势场的比值为
(3)

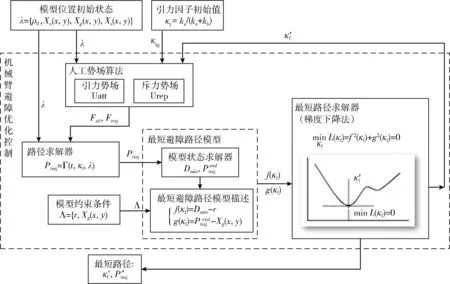
2 基于引力因子的最短路径规划模型
经过对人工势场法相关参数的分析,确定了斥力势场作用范围常数ρ0为障碍物与目标点距离,引力势场系数ka、 斥力势场系数kb的比值 (ka/kb) 变化影响着机械臂末端的运动路径。然而,对于在机械臂实际的工作环境中,对于不同位置和大小的障碍物,模型参数如何设定能够获取最短避障路径是本文关注的重点问题。因此,在本节中将构建基于引力因子的最短避障路径规划模型,求解机械臂末端最短路径及参数,使机械臂末端能够以最短路径避开障碍物并达到目标点。
2.1 机械臂避障模型
工业SCARA的平面两自由度Matlab机械臂避障模型如图3所示,图中采用平面两自由度机器人,该机构常用于平面多关节工业机器人(SCARA工业机器人)中。定义如图3所示的以机器人肩关节中心的机器人笛卡尔坐标系,机器人第一关节角度为q1,第二关节角度为q2。本模型对障碍物进行简化,定义障碍物区域外接圆做简化描述障碍物。其中,Xo(x,y) 为圆心坐标,r为圆半径。该方法尽管增加了障碍物区域,但极大地简化了对障碍物的描述,方便模型的建立,能够提高避障路径规划的效率。
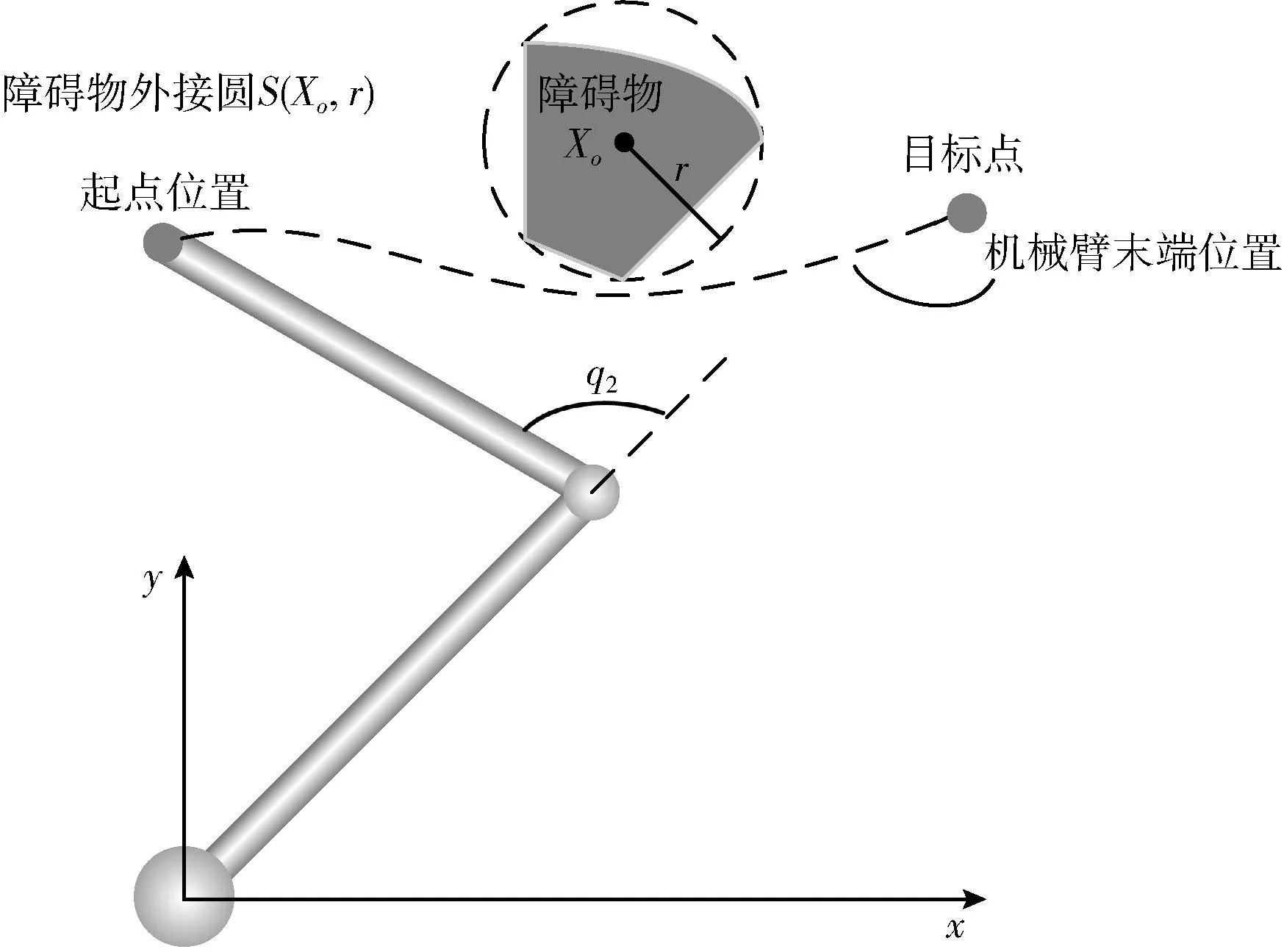
图3 工业SCARA平面两自由度机械臂避障模型
对于任意位置和大小的障碍物,确定斥力势场作用范围常数ρ0等于障碍物位置与目标点位置距离后,机械臂末端运动路径的变化由引力势场系数ka、 斥力势场系数kb的比值 (ka/kb) 决定。本文将建立机械臂最短避障路径规划模型,通过对非线性目标函数求最优解,得到机械臂的最优路径。
2.2 机械臂最短路径规划算法
由1.3节分析可得 (ka/kb) 保持不变时,机械臂末端的路径不变。ka/kb增大时机械臂末端避障路径弧度会变小,反之,机械臂末端避障路径弧度则会变大。当ka远远大于kb或ka远远小于kb时,ka/kb处于无穷大和无穷小的状态,这对于我们分析参数对避障路径的关系增加了难度,为了使现象和结果更加直观,定义引力因子κf
κf=ka/(ka+kb)
(4)
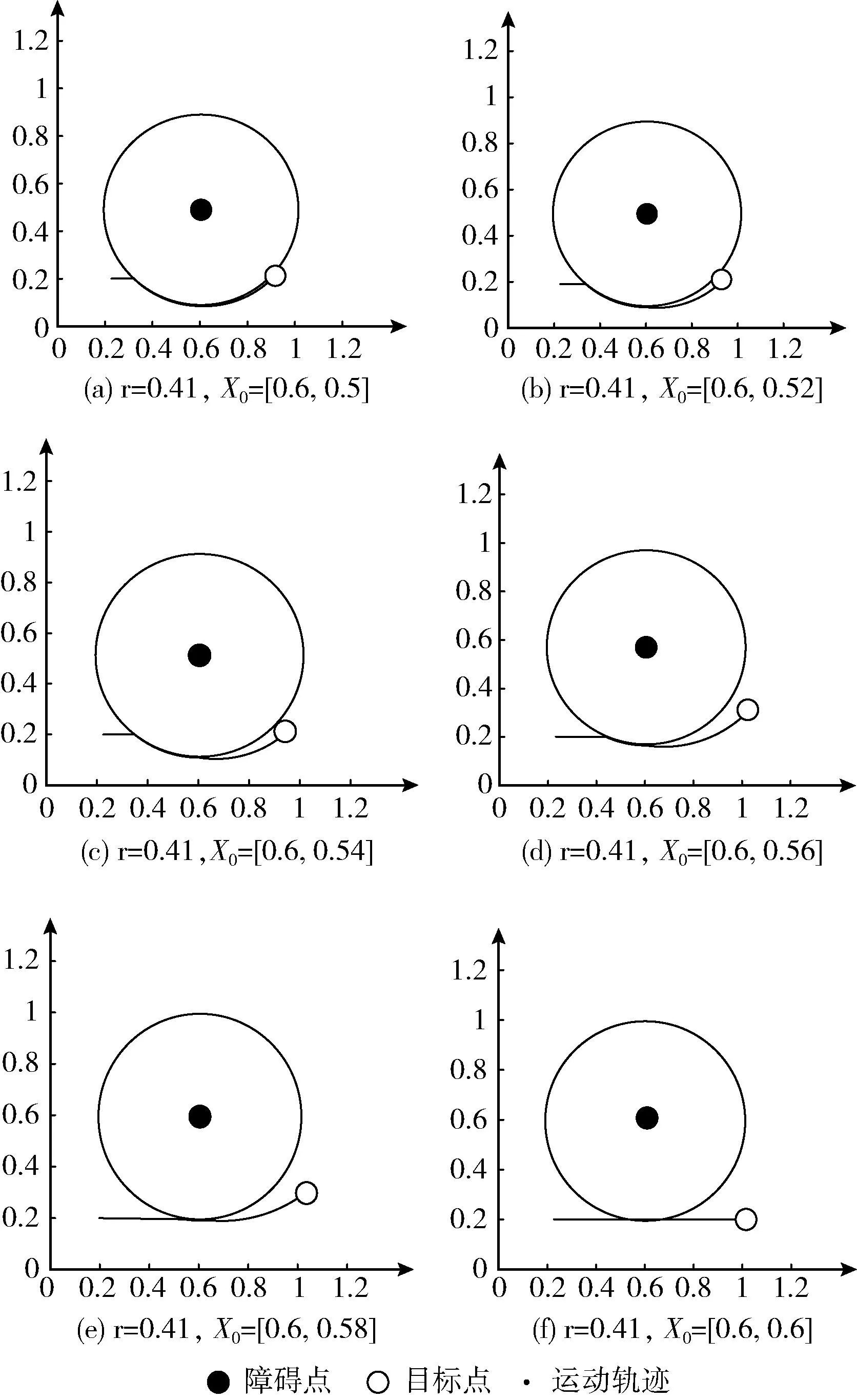
其中,当引力势场系数ka所占比例越大,κf则越大,机械臂末端避障路径弧度会变小,ka/kb无穷大时κf极值为1;反之,机械臂末端避障路径弧度会变大,ka/kb无穷小时κf极值为0。通过定义该引力因子,使我们能够更加直观有效地研究机器人的最短避障路径。
机械臂末端从起始位置出发到达目标点位置,在运动过程中,研究机械臂的避障问题,时刻需要关注机械臂末端位置与障碍物中心位置之间的距离,防止机械臂与障碍物的碰撞。令机械臂末端运动路径点的集合为Ptraj
Ptraj=Γ(t,κf,λ)
(5)
其中,Ptraj为机械臂末端运动路径函数,能够表示出机械臂末端任意时刻所在的位置;Ptraj与t,κf,λ有关,其关系函数定义为Γ(t,κf,λ), 表明了机械臂末端运动路径与t,κf,λ之间的关系。其中t为机械臂末端运动的时间;κf为引力因子;对于指定的障碍物和目标点信息,λ为一组常数如式(6)所示
λ={ρ0,Xo(x,y),Xg(x,y),Xt(x,y)}
(6)
其中,ρ0为斥力势场作用范围常数,Xo(x,y) 为障碍物的位置,Xg(x,y) 为目标点的位置,Xt(x,y) 为机械臂末端初始位置。
在机械臂末端运动路径点的集合Ptraj中,存在与障碍物中心Xo(x,y) 距离最短的点xmin(x,y), 定义该最短距离为dmin(图4)
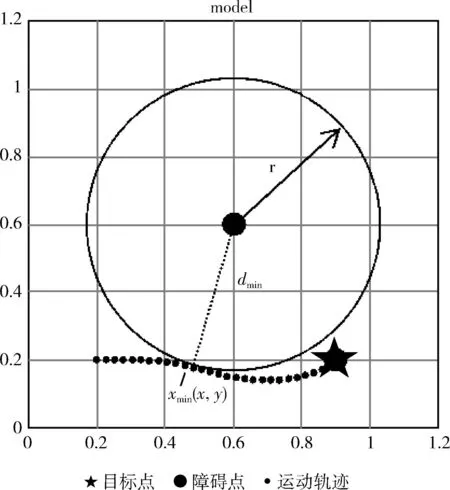
图4 机械臂末端的最短避障路径规划
dmin=Φmin(κf,λ)
(7)
其中,κf为引力因子;λ如式(6)所示为一组常数;dmin与κf、λ有关,Φ表示了最短距离dmin与κf与λ之间的函数关系。
机械臂末端的最短避障路径规划如图4所示,机械臂末端的最短避障路径,在路径平面内,圆形表示障碍物区域,实心大圆代表以Xo(x,y) 为圆心r为半径的障碍物,五角星则代表目标点的中心点位置,实心圆点状路径为机械臂末端从起点到目标点的运动路径,其集合为Ptraj。
机械臂末端从起始位置出发到达目标点位置,在运动过程中,机械臂的碰撞检测问题可以被描述为路径末端Ptraj到障碍物中心点Xo(x,y) 最小距离dmin与障碍物的半径r之间的关系问题:
(1)dmin (2)dmin=r,则表示机械臂末端与障碍物外接圆处于相切的状态,存在唯一解,此临界状态为机械臂避障的最短路径。 (3)dmin>r,则表示机械臂末端处于障碍物范围之外,存在多个解,机械臂末端未与障碍物发生碰撞现象。在多个解中,存在可以近似认为机械臂末端轨迹与半径r的圆相切,此时状态下,机械臂末端的路径长度大于(2)中的情况。因此,当dmin=r时,机械臂末端从起始点到达目标点的路径最短。 当机械臂末端路径经过最短路径到达目标点时,则该运动状态模型可以被描述为 (8) (9) (10) 图5 基于人工势场引力因子的机械臂最短避障路径规划控制流程 则构建避障路径的目标函数 L(κf)=f2(κf)+g2(κf) (11) (1)给定初值κf0∈R0, 允许误差ε>0, 令k=0。 (4)选择步长因子μk>0, 以保证L(κfk+μkhk) (5)计算κfk+1=κfk+μkhk。 (7)置k=k+1,转第(1)步。 本节设计改变障碍物半径和障碍物纵坐标位置的适应性实验,研究不同障碍物大小和位置的最短路径的特征以及机械臂的关节角度路径特征,本文在Matlab中搭建了SCARA机器人实验平台,并进行了相关算法的验证。与传统人工势场法相比,本文提出的算法在求解避障最短路径的同时,实现了运动轨迹与障碍物半径的相切控制,并取得了较好的控制效果。 表1 不同障碍物半径的路径参数 图6 障碍物半径变化的机械臂末端路径 图7 障碍物半径r与引力因子的关系 表2 不同障碍物圆心位置的路径参数 图8 障碍物位置变化的机械臂末端路径 图9 障碍物纵坐标y与引力因子的关系 上述讨论针对不同圆心位置和半径的障碍物,机械臂末端轨迹与障碍物外切圆相切且又能收敛到末端的最短避障路径。对于不同的末端路径,本节基于工业SCARA机器人的平面模型对机械臂的关节路径进行求解分析。关节路径通过机器人逆运动学计算得到。 本节选择图6(a)和图6(c)的机械臂末端最短避障路径为例,其中障碍物半径r分别为0.4和0.44,中心位置为(0.6,0.6),目标点为(0.9,0.2),机械臂末端起始位置(0.2,0.2)。图3所示平面两自由度机械臂模型大臂和小臂长度分别为0.4 m和0.35 m。设置避障模型坐标系原点在机械臂坐标系的(-0.5,0.3),从而使机械臂能够在运动空间范围内完成避障运动任务。通过控制机械臂的两个关节电机,使得机械臂末端精确跟踪最短避障路径。 通过机器人逆运动学计算得到两种情况的机械臂关节角度变化情况如图10所示,横坐标为无量纲的时间坐标,纵坐标表示关节角度,其中五角星表示大臂关节角度q1,实心大圆表示小臂关节角度q2,可以看到虚线为r=0.4情况,机械臂小臂关节先增大后减小,大臂关节先减小再增大,从而实现机械臂末端的直线运动。在机械臂开始运动时,图中两种情况的关节运动基本相同。当r=0.44情况下机械臂末端在t∈[0.2,1] 时间段内,相比r=0.4情况机械臂小臂关节增大更多的角度,而同时大臂减小更多的角度,这主要是因为当r=0.44情况的机械臂末端出现弧线路径,使得机械臂需要摆动更多的角度实现避障运动。 图10 最短避障路径的机械臂关节角度变化情况(r为0.4和0.44) 本文提出一种基于人工势场的机械臂最短避障路径规划模型,以引力因子κf为核心,求解机械臂二维平面内的最短避障路径。结果表明:当ρ0等于障碍物与目标点距离时,机械臂末端在运动过程中的轨迹较为平滑并最终能够到达目标点;比值ka/kb与避障路径弧度的变化成反比关系,当该比值不变时,机械臂末端的运动路径不变。本文提出的算法能够准确适应障碍物位置和大小的变化,满足机械臂末端在最短空间状态下避障的要求。与传统人工势场法相比,本文提出的算法在求解避障最短路径的同时,实现了运动轨迹与障碍物半径的相切控制,并取得了较好的控制效果。进一步为机器人路径规划研究提供理论意义,同时也为改进人工势场法提供分析思路。
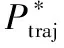
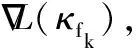

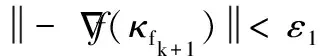
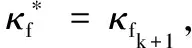

3 实验与讨论
3.1 障碍物大小变化情况的最短路径特征分析
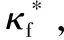
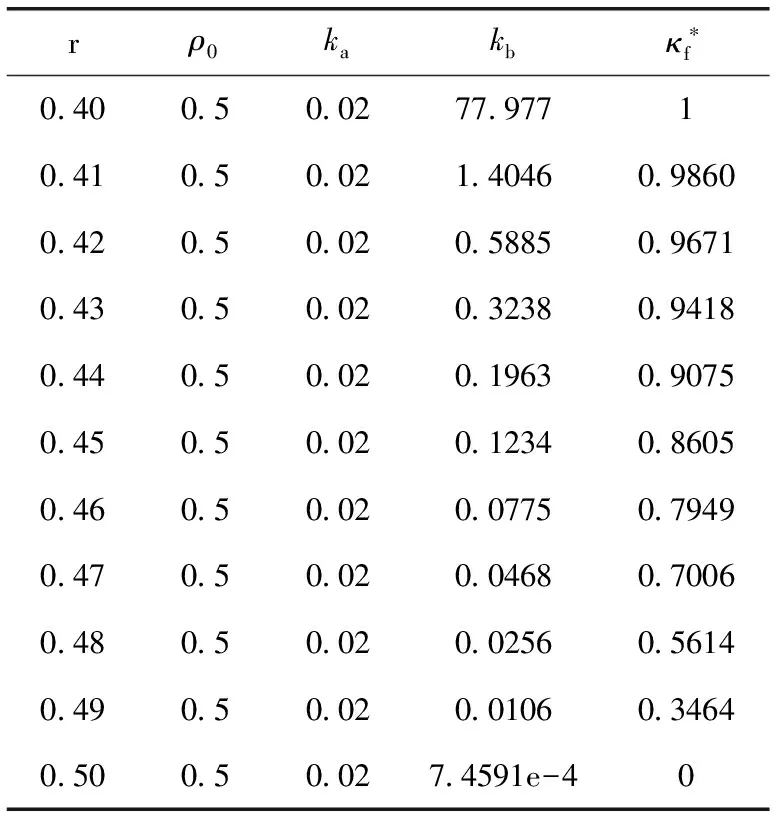
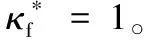
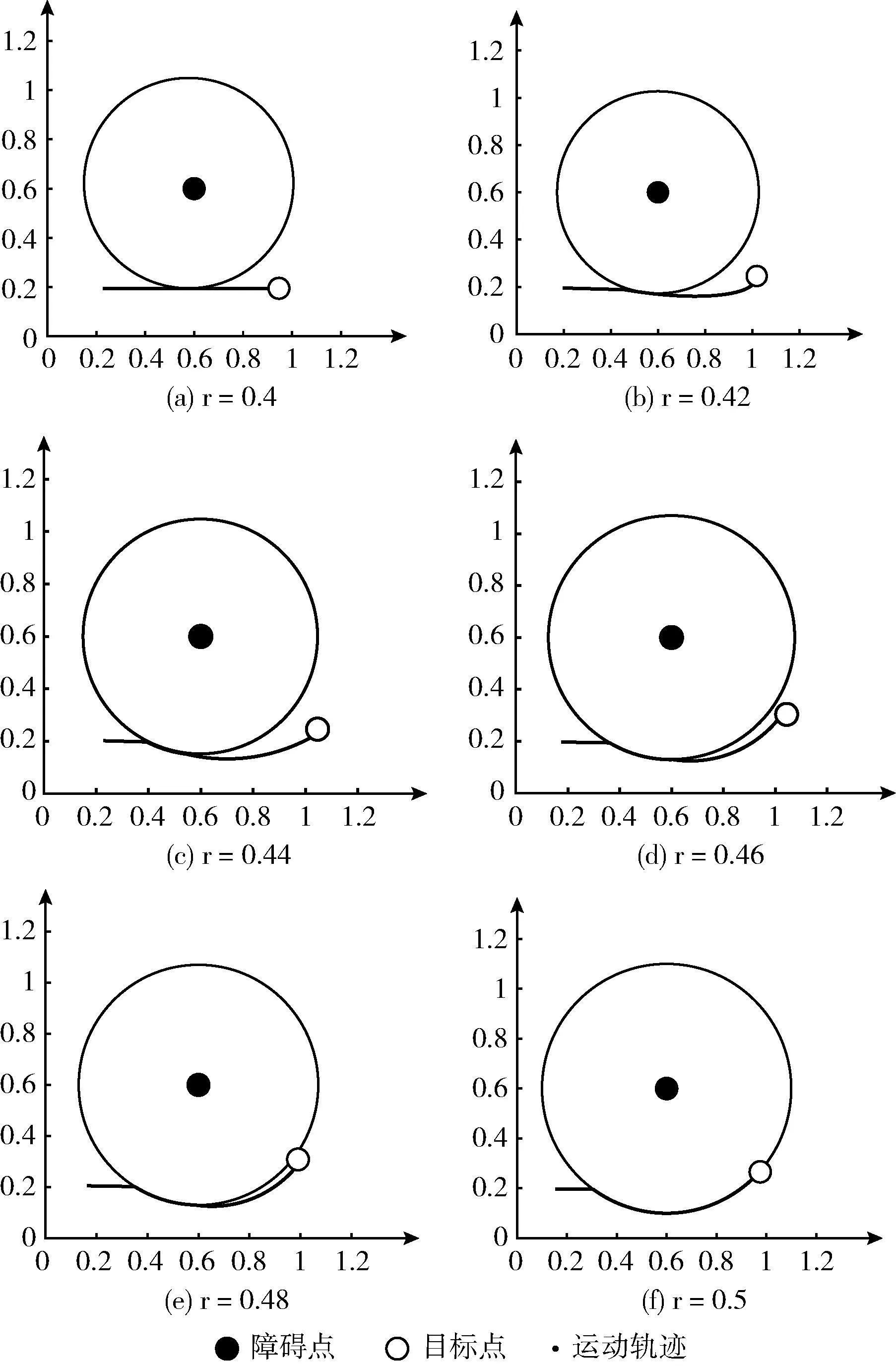
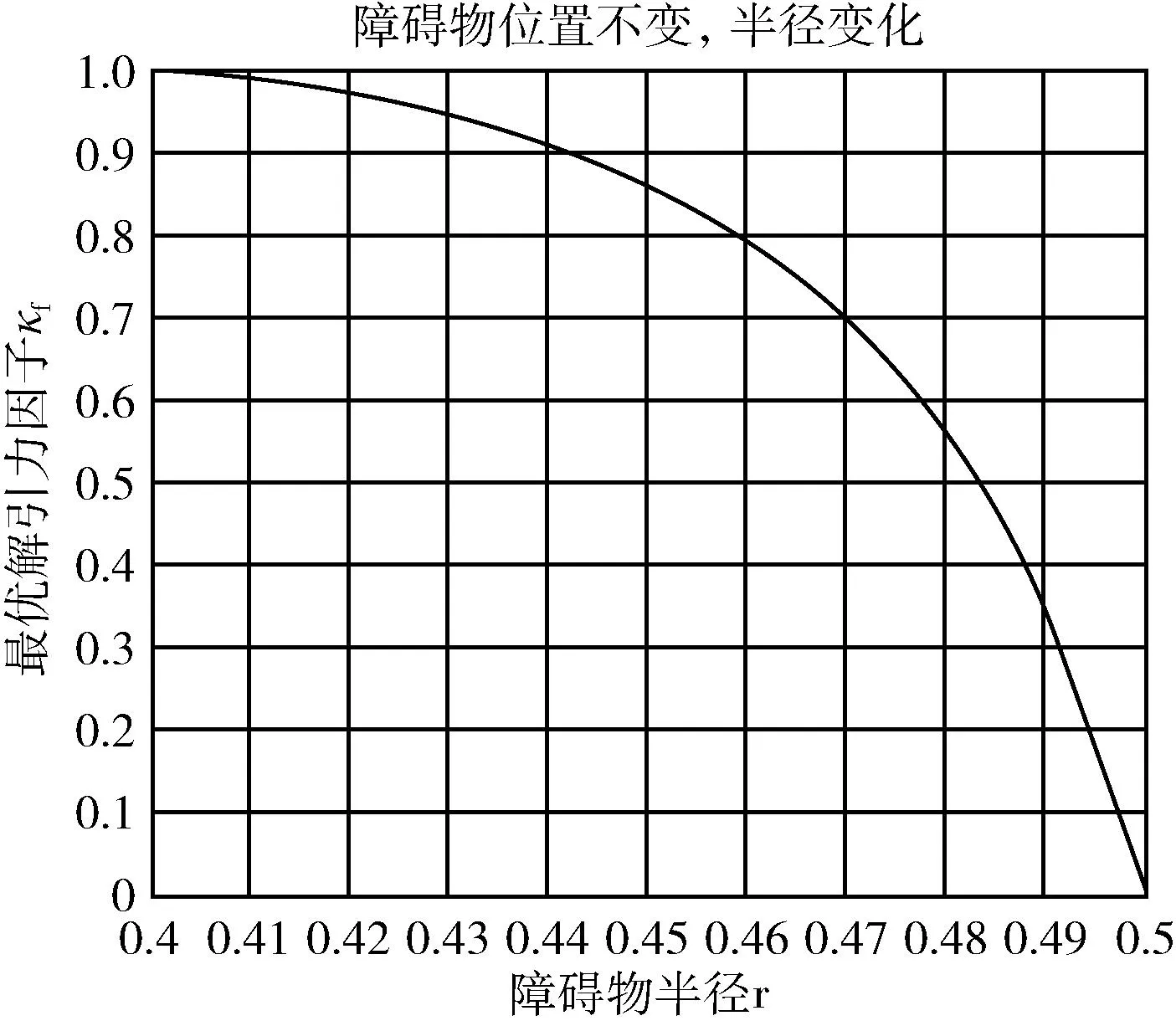

3.2 障碍物圆心位置变化情况的最短路径特征分析
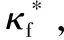



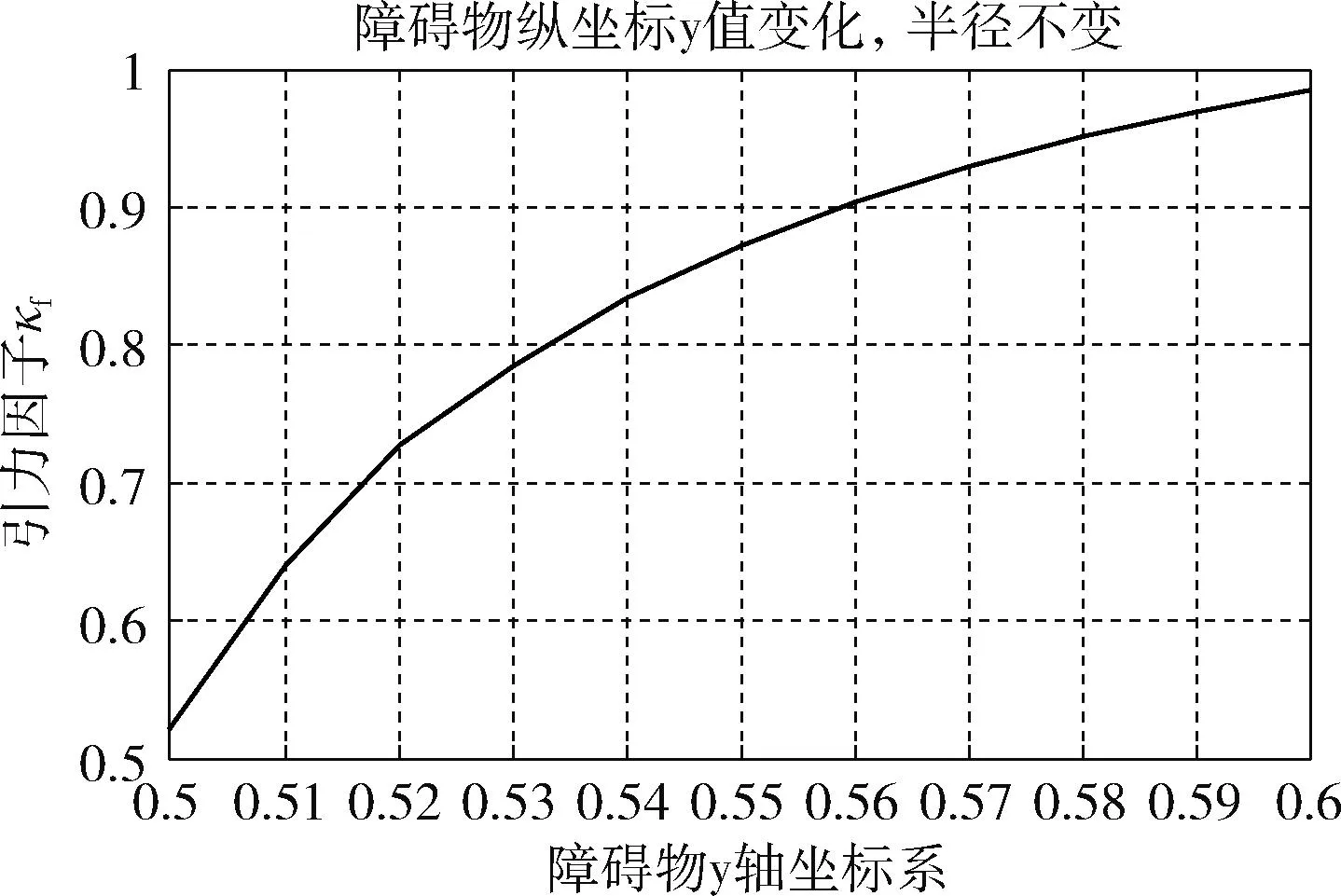

3.3 机械臂关节路径分析

4 结束语

