基于Transformer的飞机状态预测

王经纬，高艳鹍，宋澣兴，刘一非

(1.中国航空研究院 中国航空系统工程研究所，北京 100029；2.中国航天科工集团第二研究院七〇六所，北京 100854；3.北京邮电大学 计算机学院，北京 100876；4.北京工商大学 计算机学院，北京 100048)

0 引 言

在大迎角飞行过程中，由飞机表面流场复杂变化及涡的破裂等导致气动力呈现强烈的非线性特性，严重影响飞行安全和飞机效能。现阶段，非定常气动力建模是解决大迎角问题的主要方法之一[1]。

对飞行状态的预测作为气动力建模的一个分支，传统方法较复杂，成本高，样本数据需求量大，且存在提取时间关联信息能力弱、性能表现差等弊端。随着人工智能技术的兴起，智能方法如神经网络模型、支持向量机模型等陆续应用到飞行状态预测，这些方法规避了对复杂流体的机理研究，属于黑箱非线性系统建模，学习能力强，效果显著。

由于预测飞行状态需要同时预测飞行状态参数与飞行状态类别，且二者相辅相成，实际上是一种回归与分类相结合的问题。为更好解决这一问题，本文提出了一种多任务Transformer模型，能够同时进行回归与分类，通过实验与其它方法进行对比，多任务Transformer模型在飞行状态参数回归上至少有21.6%的性能提升，在飞行状态分类上至少有4.1%的性能提升。

本文主要创新点如下：

(1)提出了一种基于多任务Transformer的模型用于飞机状态预测；

(2)使用Transformer模型同时进行飞行状态参数的预测与飞行状态分类，模型的Query、Key和Value集将飞机状态参数特征进行融合，同时，通过分配预测任务与分类任务损失函数的不同比重，改进了Transformer模型结构，更好适应了应用场景；

(3)飞机仿真数据实验结果表明，本文提出的模型在性能上优于现有LSTM预测模型，且与单任务Transformer模型相比也表现出了一定优势。

1 相关工作

随着神经网络的不断发展，国内外学术领域在非定常气动力建模方面的探索不断深入，主要从反向传播(back propagation，BP)、循环神经网络(recurrent netual network，RNN)，到支持向量机(support vector machine，SVM)，均取得了一定进展。王海峰等[2]介绍了BP神经网络的相关方法。何磊等[3]采用LSTM循环神经网络对振荡三角翼的非定常气动力进行建模，取得了收敛速度快、预测精度高、且泛化性良好等效果。Kou J等[4]利用LSTM进行飞机失速预测建模；陈翔等[5]验证了LSTM神经网络模型应用在非定常气动力建模上的优势。何磊等[6]使用支持向量机方法也取得了较好预测效果。

近年来，Transformer模型架构一枝独秀，在视觉[7，8]、语音[9-12]、目标检测[13-16]等领域都取得了很好的效果，作为时序预测较前沿的方法之一，本文基于该架构提出了一种基于多任务Transformer模型的飞机状态序列预测方法，通过对比实验，在回归任务与分类任务上表现良好，有着很高的应用前景。

2 基于多任务Transformer的飞机状态序列预测方法

由于使用人工智能方法预测飞机状态序列属于较新兴的研究领域，能借鉴的经验方法较少。在充分研究、分析飞机仿真数据后，我们提出了多任务Transformer预测方法，下面主要介绍方法涉及的基本概念和细节。

2.1 基本概念

定义1 飞行状态参数序列集合。飞机的飞行状态参数序列为某一时刻的各项气动力参数(状态点参数)，包括飞行速度、飞行高度、迎角、侧滑角、俯仰角、旋转角、俯仰角速度、偏航角速度等。飞机的飞行状态参数序列集合由一段连续的状态参数序列构成，表示为T={T1，T2，…，TN}， 其中N为所有飞行状态参数序列总数。飞行状态参数序列集合中的第i条飞行状态参数序列由Ti={(α1，β1，p1，q1，r1，l1)，…，(αN，βN，pN，qN，rN，lN)} 表示，其中 (αm，βm，pm，qm，rm，lm) 表示飞行状态序列中的第m个状态点，αm表示第m个状态点的迎角，βm表示第m个状态点的侧滑角，pm表示第m个状态点的滚转角速度，qm表示第m个状态点的俯仰角速度，rm表示第m个状态点的偏航角速度，lm表示第m个状态点的状态标识。

定义2 飞行状态序列集合。当飞机的迎角超过临界迎角后，会发生的一系列大迎角异常运动。通常情况下，飞机会沿着一条小半径的螺旋线一面旋转、一面急剧下降。飞行状态序列集合对应飞机的所有飞行状态(正常、异常)，记为W={W1，W2，…，WN}， 其中N为所有飞行状态参数序列总数。其中一条飞行状态由Wi={w1，w2，…，wN} 表示，其中wm表示该飞行状态序列第m个状态点的飞行状态标签，wm∈{0，1，2，3，4}。 其中，0表示正常，1～4表示4种异常状态，属于大迎角异常状态。

定义3 多任务损失函数。本文研究重点在于基于多任务Transformer模型完成两个任务：任务1-飞行状态参数回归和任务2-飞行状态分类。多任务损失函数即模型总损失函数由loss=rate1*loss1+rate2*loss2表示，loss1为任务1的均方误差，loss2为任务2的交叉熵误差，rate1为任务1损失函数的权重系数，rate2为任务2损失函数的权重系数。

2.2 多任务Transformer模型架构

2.2.1 Model Encoder模块

图1展示了本模型的架构。本模型主要由Model Encoder模块、Model Decoder模块以及多任务生成模块组成。

图1 多任务Transformer模型结构

Model Encoder模块对当前飞行状态参数序列进行特征提取，然后为其添加位置编码信息，最后通过输入Model Encoder提取参数序列的高维特征。

当前飞行状态参数序列表示为T0∈Rbatch_size×p×t， 其中batch_size为数据批量大小，p为Model Encoder输入序列的状态点数量，t为状态参数维度，即一个状态点中选取特征参数的个数。使用线性映射层(Linear1)对该序列进行特征提取，得到数据特征序列T1

T1=T0*WLinear1

(1)

其中，WLinear1∈Rt×d，T1∈Rbatch_size×p×d，d为模型内隐向量维度。

此时，T1不包含位置编码信息，需要使用Position Embedding为T1添加位置编码信息。Position Embedding表示为

PE(pos，2i)=sin(pos/10002i/d)

(2)

PE(pos，2i+1)=cos(pos/10002i/d)

(3)

其中，pos为飞行序列中的第pos个状态点，i为其中第i个维度。

经过位置编码模块后，得到包含位置信息的数据特征序列T2

T2=T1+PE

(4)

其中，T2∈Rbatch_size×p×d，PE∈Rbatch_size×p×d。

然后，使Transformer Encoder模块提取更高维度的数据特征序列T3。 本方法使用2层的Transformer Encoder，每层是由一个多头注意力网络和一个前馈神经网络(FFN)构成的。其中多头注意力的公式为

MultiHead(Q，K，V)=concat(head1，…，headh)W0

这里

(5)

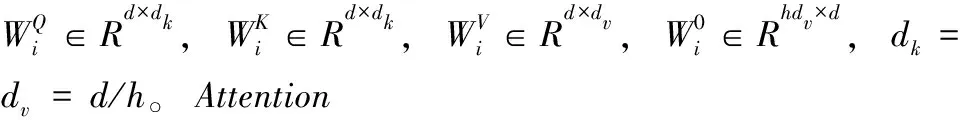
(6)

在多头注意力层之后的前馈神经网络的公式为

FFN(x)=max(0，xW1+b1)W2+b2

(7)

其中，W1∈Rd×df，W2∈Rdf×d，x为多头注意力网络的输出。

特征升维过程可表示为可以描述为

T3=TransformerEncoder(T2，T2，T2)

(8)

其中，T3∈Rbatch_size×p×d。

2.2.2 Model Decoder模块

Model Decoder模块结构与Model Encoder的结构一致，首先对预测序列进行数据处理，然后添加位置编码信息，最后输入至Transformer Decoder提取高维数据特征。

本方法中的回归任务为多步预测，需要将预测出的飞行状态参数序列与Model Decoder模块的输入序列进行拼接。拼接后序列表示为T′0∈Rbatch_size×p×t， 其中batch_size为数据批量大小，p为预测飞行状态参数序列的状态点数量，t为状态参数维度。使用另一个线性映射层(Linear2)对T′0进行特征升维，得到数据特征序列T′1

T′1=T′0*WLinear2

(9)

其中，WLinear2∈Rt×d，T′1∈Rbatch_size×p×d，d为模型内向量维度。

使用与Model Encoder相同设计的Position Embedding层为T′1提供位置编码信息PE′， 得到具有位置编码信息的数据特征序列T′2

T′2=T′1+PE′

(10)

其中，T′2∈Rbatch_size×p×d，PE′∈Rbatch_size×p×d。

最后，使用Transformer Decoder模块生成高维数据特征序列T′3， Transformer Decoder的过程与Transformer Encoder一致，可描述为

T′3=TransformreEncoder(T3，T′2，T′2)

(11)

其中，T′3∈Rbatch_size×p×d。

2.2.3 多任务生成器

数据经过Model Encoder和Model Decoder后，使用多任务生成器完成任务1-飞行状态参数回归和任务2-飞行状态分类。

对于任务1-飞行状态参数回归，使用一个线性映射层(Linear3)进行特征提取，得到任务1中间向量

Ttask1=T′3*WLinear3

(12)

其中，WLinear3∈Rt×d，Ttask1∈Rbatch_size×p×d。

接着，使用一个线性映射层(Status Predictor)得到预测结果的输出向量

Output1=Ttask1*WStatusPredictor

(13)

其中，WStatusPredictor∈Rd×t，Output1∈Rbatch_size×p×t。

对于任务2-飞行状态分类，使用一个线性映射层(Linear4)进行特征提取，得到任务2的中间向量

Ttask2=T′3*WLinear4

(14)

其中，WLinear4∈Rd×d，Ttask2∈Rbatch_size×q×d。

最后，使用线性映射层(Type Classify)进行状态分类得到任务2的输出向量

Output2=argmax(Ttask1*WTypeClassify)

(15)

其中，WTypeClassify∈Rt×type_num为一个全连接层，type_num为飞行状态的种类数。任务2输出Ttask2∈Rbatch_size×q×type_num。

3 实验设计

3.1 数据集

本文的实验数据集主要由某型机模拟仿真数据组成。实验数据集中共包括2000条时序序列数据文件(每个文件包含5000～8000条飞行状态点)。其中每个序列的飞行状态参数由5维特征参数(迎角、侧滑角、滚转角速度、俯仰角速度、偏航角速度)和1维飞行正常状态标签(取值0/1)组成。实验数据集共计1 082 435个飞行状态，其中包括592 647个正常飞行状态和489 788个异常飞行状态。

根据时序序列特点，本文实验使用滑动时间窗口方法对数据进行划分，窗口大小为P+Q，步长为P+Q，P、Q分别为输入序列条数和预测序列条数，即选取窗口内前P个飞行状态参数序列作为模型输入数据，窗口内后Q个状态参数序列作为真值数据。

3.2 对比方法

为测试本文提出的多任务Transformer模型效果，实验主要通过与两个现有方法以及两个本方法的单任务版本效果进行对比。这4个方法分别是：

(1)Seq2Seq(Linear)[2]：双层的线性层模型被使用在进行大迎角非定常气动力建模中，建模过程的重点是调整权重，使输出层与实际值误差达到最小。我们将双层L应用在Seq2Seq结构上，得到了该方法Seq2Seq(Linear)。

(2)LSTM[5]：这是一个利用LSTM进行飞机失速预测建模的方法，LSTM循环神经网络能够在失速之前学习各种相关参数的独特时间演变，并可以提前很长时间预测潜在的失速能力，可以有效提出失速预警。

(3)Transformer(task1)[9]：这是本模型的一个单任务版本，是通过去除多任务生成器模块中飞行状态分类功能得到的。该方法仅保留本模型中飞行状态参数回归功能。

(4)Transformer(task2)[9]：这是本模型的另一个单任务版本，是通过去除多任务生成器模块中飞行状态参数回归功能得到的。该方法仅保留本模型中飞行状态分类功能。

3.3 实验设置

为了确保公平性，本实验采用相同的Adam优化器以及损失函数，并使用了相同的超参数，见表1。为了确保多任务学习中两个任务的损失函数值的数量级接近，本实验设置任务1权重系数为1，任务2权重系数为0.0001。

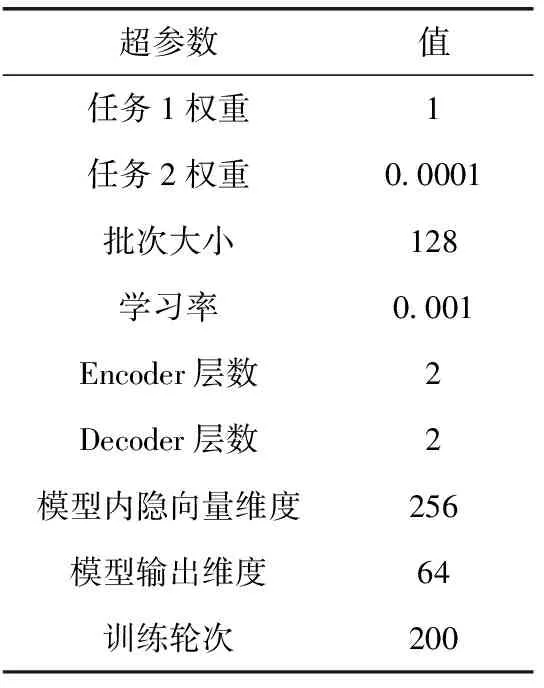
表1 超参数设置

值得注意的是，相较于分别使用Transformer(task1)和Transformer(task2)完成任务1-飞行状态参数回归和任务2-飞行状态分类，本文提出的多任务Transformer可以同时完成这两个任务，因此在参数规模、时间开销上达到事半功倍的效果。

为了更好贴近实际应用场景，体现小规模训练数据、大步长预测的特点，本实验在模型训练过程中使用前20步时序数据完成后5步飞行状态参数回归和飞行状态分类，在测试过程中使用相同数量的前序数据，完成后30步、60步、90步的飞行状态参数回归和飞行状态分类。

3.4 性能评测指标

对于任务1-飞行状态参数回归选用RMSE和MAE进行评估。

RMSE的计算方式为计算所有飞行状态参数回归值与真值的均方根误差之和，MAE的计算方式为计算所有飞行状态参数回归值与真值的平均绝对值误差之和。RMSE的计算方式为

(16)

其中，T为预测特征的个数，Numall为测试集中所有状态点的总数，Sj，i为在第j次预测中第i个特征的模型输出值，gdj，i为在第j次预测中第i个特征对应的真值。

在本实验中，不同特征的rmse值也可以用rmset表示，t∈{α，β，p，q，r，l}，rmset的公式为

(17)

其中，Numall为测试集中所有状态点的总数，Sj，t为在第j次预测中特征t的模型输出值，gdj，t为在第j次预测中特征t对应的真值。

MAE计算方式为

(18)

其中，变量与RMSE公式内变量含义一致。RMSE和MAE越小说明飞行状态参数回归误差越小，模型性能表现越高。

对于任务2-飞行状态分类选用ACC和RECALL估表现方法。ACC的计算方式为计算所有状态分类正确的比例，RECALL的计算方式为计算异常飞行状态被正确分类的比例。ACC和RECALL的公式分别为

ACC=rightall/Numall

(19)

其中，rightall为所有飞行状态分类正确总数，Numall为测试集中所有状态点数量

RECALL=rightabnormal/Numabnormal

(20)

其中，rightabnormal为异常飞行状态分类正确总数，NUMabnormal为所有异常飞行状态数量。

ACC越大代表对于飞行状态的分类准确率更高，模型表现越好；RECALL越大代表异常飞行状态被正确分类的概率更高，模型性能表现越好。

4 实验结果分析

4.1 总体对比

表2～表7分别对比了4种方法在预测30、60、90步时的RMSE、MAE和ACC、RECALL。由表2可知，在预测步数为30步的任务1-飞行状态参数回归任务上，本方法取得最好的RMSE和MAE表现，分别为0.576和0.369。相比于算法Seq2Seq(Linear)和LSTM算法，多任务Transformer在RMSE方面分别降低了0.195(25.3%)和0.159(21.6%)，在MAE方面分别降低了0.247(40.1%)和0.152(29.2%)。验证了在多任务架构下，使用Transformer模型的优越性；相比于Transformer(task2)有0.064(10%)的RMSE下降和0.039(9.6%)的MAE下降，验证多任务架构对于任务1-飞行状态参数回归效果有正向提升作用。

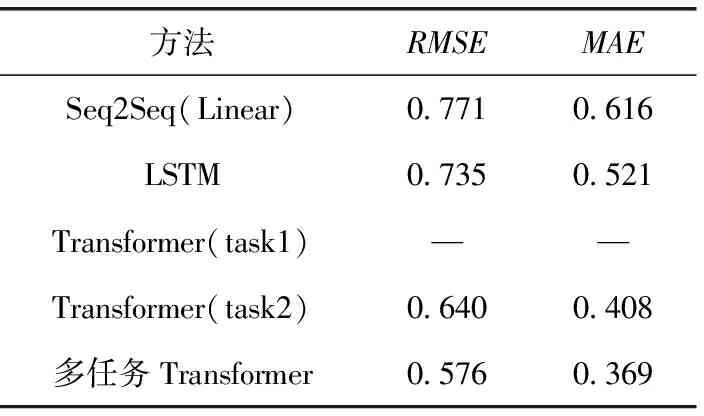
表2 预测30步时的RMSE和MAE

由表3可知，在预测步数为30步的任务2-飞行状态分类任务上，本方法相比于Seq2Seq(Linear)和LSTM在ACC方面均有0.037(4.1%)提升，在RECALL方面有0.086(10.9%)和0.084(10.6%)的提升，验证在同样使用多任务架构的情况下，使用Transformer模型的优越性。本方法与Transformer(task1)取得相同的、最好的ACC和MAE表现，分别为0.944和0.874。验证本模型使用的多任务架构在提升飞行状态参数回归性能的前提下，仍能在飞行状态分类任务上取得最好的表现。

表3 预测30步时的ACC和RECALL

由表4、表6可知，在预测步数为60步和90步的任务1-飞行状态参数回归任务上，本方法仍取得最好的表现，模型的RMSE分别为0.994和1.347，模型的MAE分别为0.642和0.865。相比于算法Seq2Seq(Linear)和LSTM算法，在预测步数为60步时，本方法的RMSE分别降低了0.493(33.2%)和0.44(30.7%)，MAE分别降低了0.570(47.0%)和0.356(35.7%)；在预测步数为90步时，本方法的均方误差分别降低了0.809(37.6%)和0.73(35.1%)，MAE分别降低了0.921(51.5%)和0.564(39.4%)，验证了使用在使用多任务架构下，使用Transformer模型的优越性；相比于Transformer(task2)，在预测步数为60步和90步时，RMSE分别降低了0.053(5.1%)和0.046(3.3%)，MAE分别降低了0.023(3.5%)和0.019(2.1%)，验证多任务架构对于飞行状态预测效果有正向提升作用。

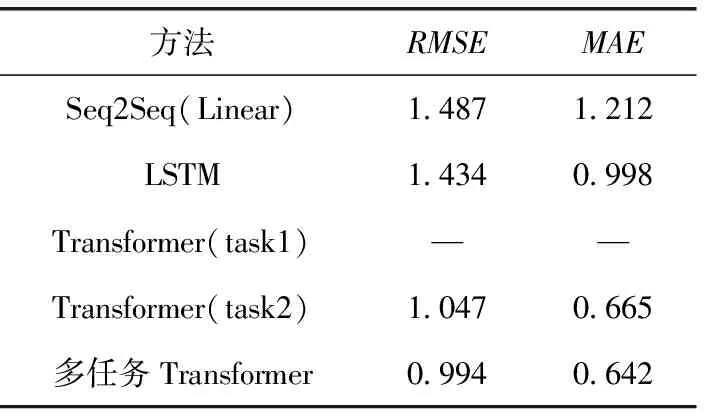
表4 预测60步时的RMSE和MAE

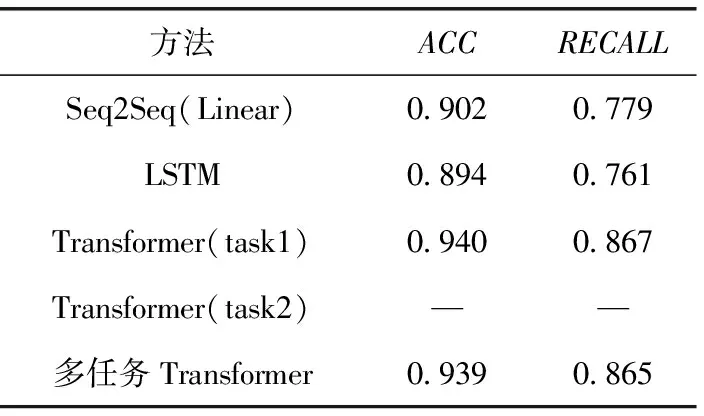
表5 预测60步时的ACC和RECALL

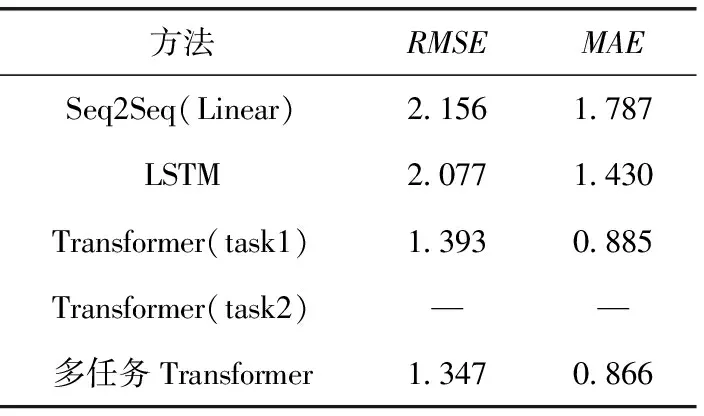
表6 预测90步时的RMSE和MAE

由表5、表7可知，在预测步数为60步和90步的任务2-飞行状态分类任务上，在预测步数为60步时，本方法相比于Seq2Seq(Linear)和LSTM在ACC方面分别有0.037(4.1%)和0.045(5%)提升，在RECALL方面分别有0.086(11%)和0.104(13.7%)提升；在预测步数为90步时，本方法相比于Seq2Seq(Linear)和LSTM在ACC方面分别有0.04(4.5%)和0.055(6.3%)提升，在RECALL方面分别有0.089(11.6%)和0.124(16.9%)提升，验证在同样使用多任务架构的情况下，使用多任务Transformer模型完成飞行状态分类任务的优越性。相比于Transformer(task1)模型，多任务Transformer在ACC方面，在预测步数为60步和90步时，均有0.001(0.1%)的轻微下降；在RECALL方面，在预测步数为60步和90步时分别有0.002(0.3%)和0.003(0.3%)的轻微下降。

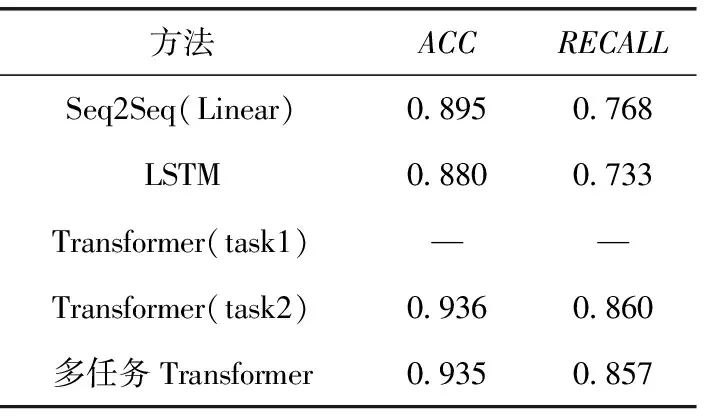
表7 预测90步时的ACC和RECALL

4.2 回归均方误差分析

对于任务1-飞行状态参数回归，本文对各个方法的参数预测效果进行了进一步分析，结果如图2、图3、图4所示。对于α、p、r特征，在预测步数为30步、60步、90步的实验中，多任务Transformer均取得稳定的、最优的效果。对于β和q特征，在预测步数为30步、60步、90步的实验中，LSTM取得了最优的效果，但是多任务Transformer取得了与LSTM较为接近的效果，与LSTM相比，在β特征上rmseβ至多高0.023。在r特征上rmser至多高0.007。对于l特征，除了Seq2Seq(Linear)效果较差外，其余方法均取得了接近的结果。

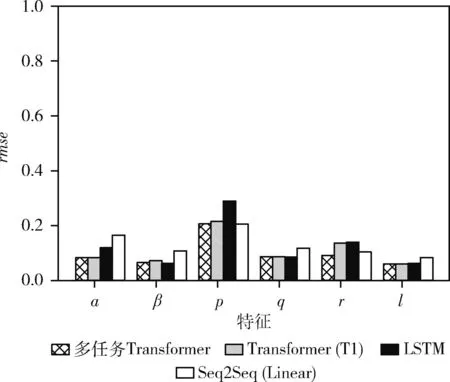
图2 预测30步时各状态特征均方误差

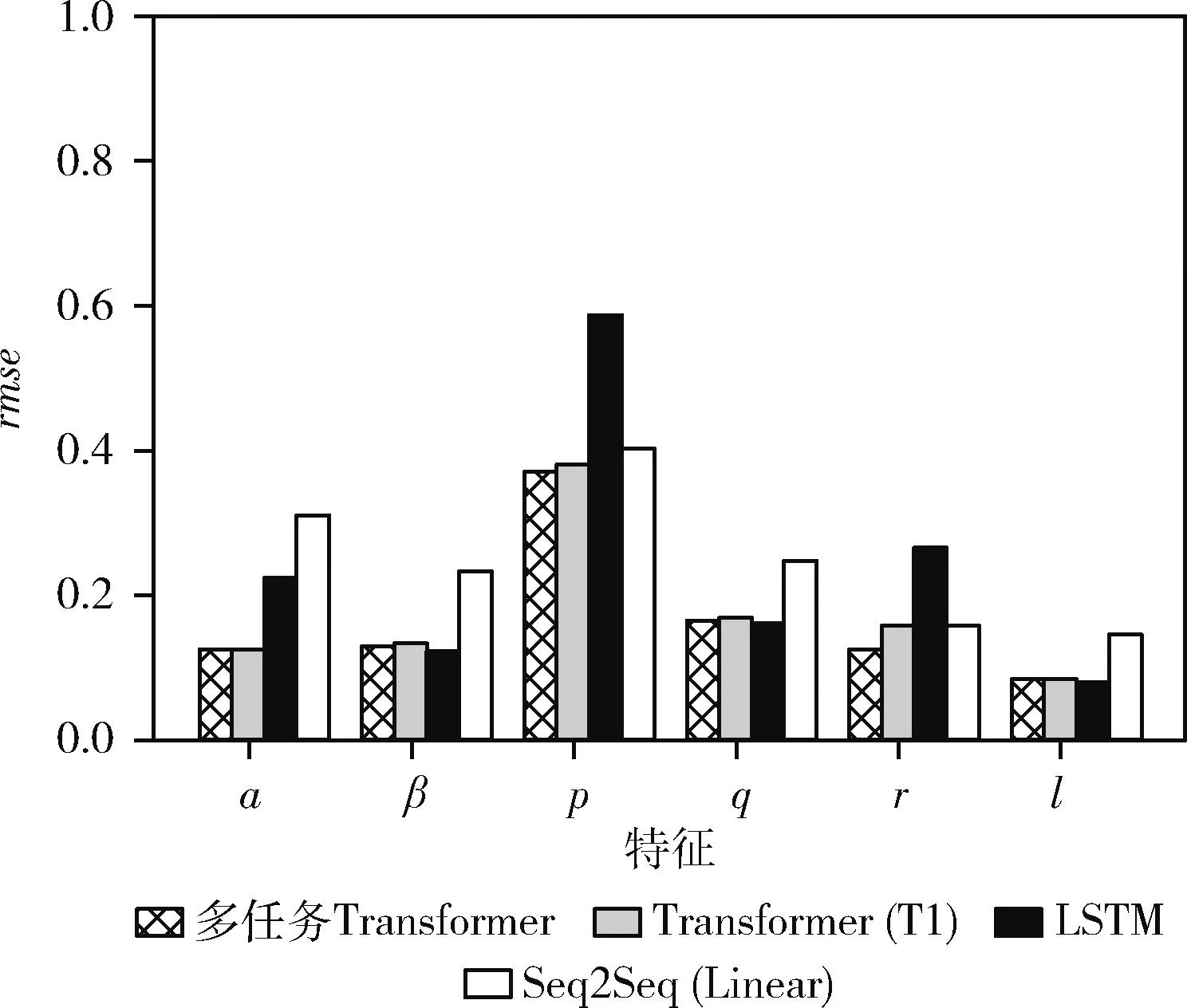
图3 预测60步时各状态特征均方误差

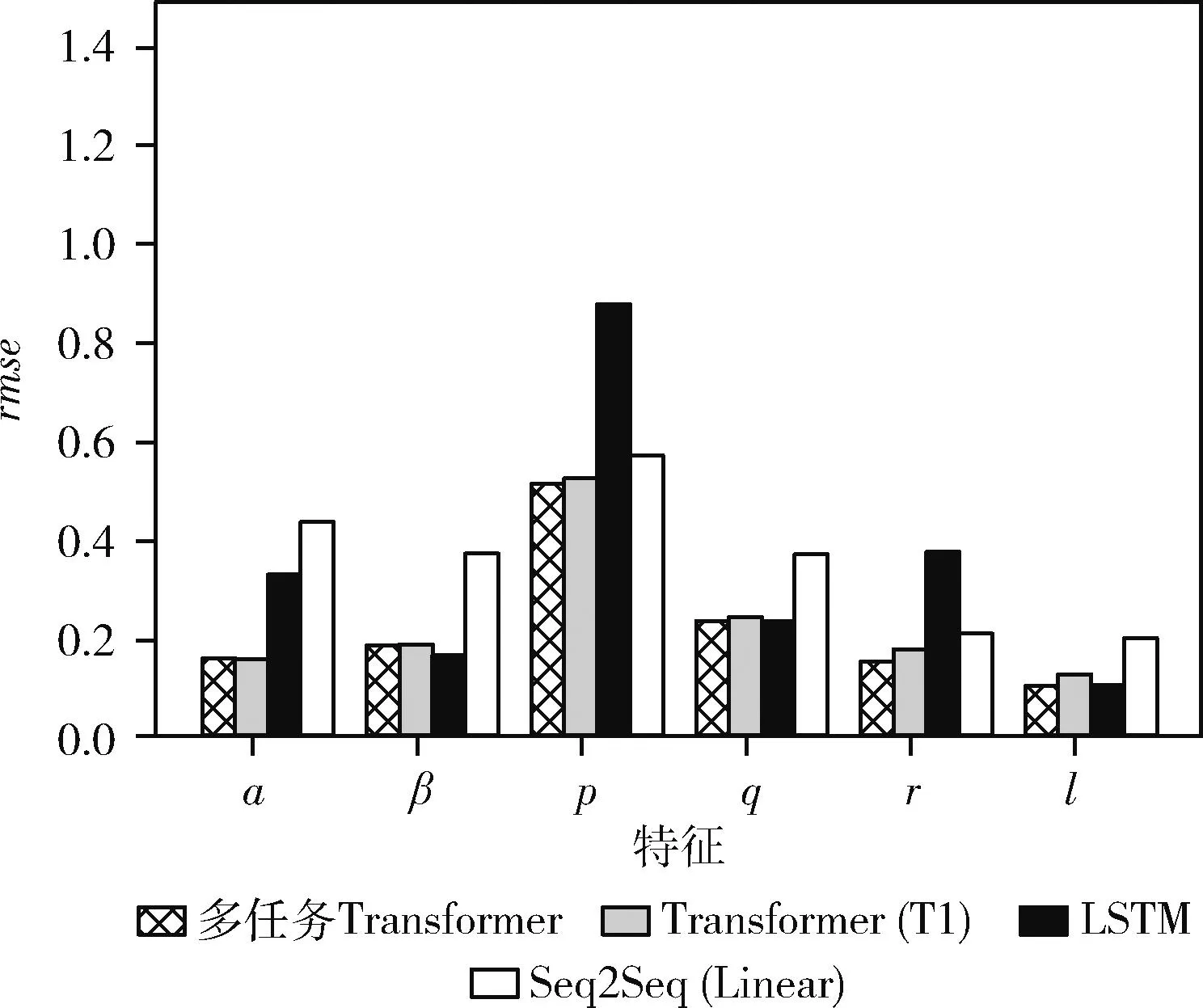
图4 预测90步时各状态特征均方误差

总体而言，多任务Transformer在飞行状态参数回归上相比于对比方法在α、p、r有绝对的性能提升，在β和q特征上有与最优方法接近的较优表现。

5 结束语

本文提出了一种多任务Transformer模型，能够同时完成参数回归任务与状态分类任务。该模型在不同的预测步数实验中的回归任务上均取得了最优的效果，相比于LSTM至少有21.6%的性能提升；在分类任务上，虽然相比于单任务版本Transformer至多有0.1%的准确率下降，但相比其它模型在准确度上均有大幅提升，尤其较LSTM至少有4.1%的性能提升。

今后，多任务Transformer模型应探索优化β和q的预测能力。同时，由于在分类任务上略差于单任务Transformer模型，将进一步研究如何设计有效的机制提升分类能力。