两相静止坐标系下基于改进型双二阶广义积分器的锁相环控制策略

韩以鑫 邹复民 侯 隽 张 青

两相静止坐标系下基于改进型双二阶广义积分器的锁相环控制策略

韩以鑫1邹复民1侯 隽2张 青2

（1. 福建理工大学电子电气与物理学院，福州 350118；2. 福建星云电子股份有限公司，福州 350000）

由于分布式新能源和多样化负荷广泛接入电网，传统基于单同步旋转坐标系的锁相环（SRF-PLL）结构在复杂工况下无法准确地跟踪电网相位、频率等参数，因此本文提出一种在两相静止坐标系下基于改进型双二阶广义积分器（DSOGI）的锁相环控制策略。首先，采用级联谐振滤波器处理低频段奇次谐波，在二阶广义积分正交信号发生器（SOGI-QSG）的基础上添加直流偏置滤除支路，在消除直流扰动、实现正负序电压解耦分离的同时，优化对高频段谐波的抑制；然后，构建ab锁相环（PLL）结构，基于小信号控制模型优化动态响应性能，提高锁相精度；最后，通过Matlab/Simulink仿真对比，证明了改进型锁相环控制策略的有效性。

二阶广义积分正交信号发生器（SOGI-QSG）；锁相环；直流偏置；级联谐振滤波器

0 引言

得益于电力电子技术近年来的发展，储能变流器等并网电气设备既能增强供电可靠性，又能改善分布式新能源电能质量。要实现储能变流器高质量并网，必须快速、精准地锁定电网相位、频率和幅值等参数，因而锁相环（phase-locked loop, PLL）成为影响分布式新能源发展的关键技术之一，具有很高的研究价值[1-3]。

基于单同步旋转坐标系的锁相环（synchronous reference frame-PLL, SRF-PLL）是实现电网同步的典型方案，因其结构简单而得到广泛应用。然而，SRF-PLL的抗干扰能力十分有限，当电网呈现非理想状态甚至存在畸变干扰时，其对电网相位与频率的提取都会产生误差波动[4-6]。

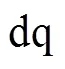
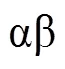
1 改进型DSOGI-QSG

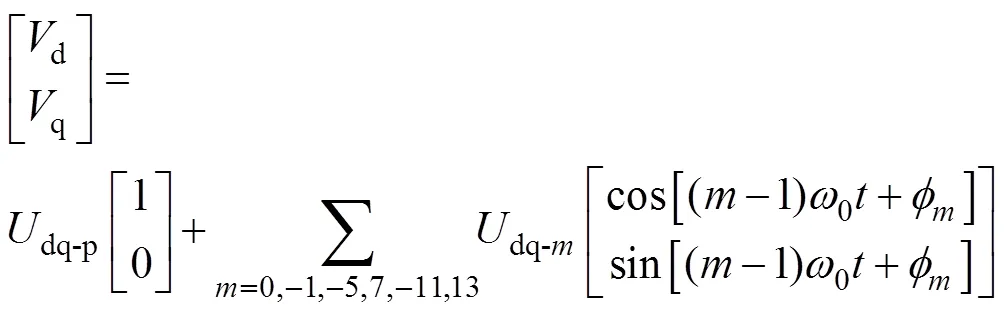
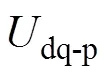
由式（1）可得电网电压的幅值和相位信息。

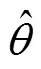
由式（2）和式（3）可知，畸变电网工况下，电网电压的幅值和旋转角频率都无法处于恒定状态，致使SRF-PLL不能准确地提取电网电压正序分量并准确追踪电网相位。

为提高PLL的抗干扰能力以适应畸变电网工况，可在锁相结构中选取合适的滤波器形式进行滤波，主要分为三类[13]：①锁相环的滤波器为复系数形式的锁相环；②在锁相控制环的内部增加环路滤波器的锁相环；③在锁相控制环的前端增加前置滤波器的锁相环。前两种滤波形式的优点在于结构简便，但是为了有效抑制低频段谐波，必须大幅度降低锁相内环的系统带宽，而且存在数字化实现困难的问题。在锁相环的前端增加前置滤波器则可排除鉴相结构对PLL结构的干扰，具有良好的响应速度和锁相精度。

1.1 带积分负反馈补偿支路的SOGI-QSG

不对称的三相电网电压利用对称分量法可分解成正序、负序和零序分量。正序和负序分量可表示为

其中

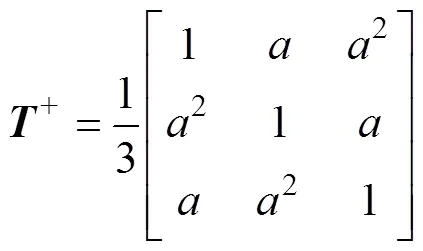
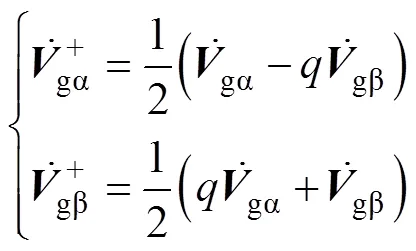
分析式（5）可知，需对电网电压的、轴分量与进行90°的移相，二阶广义积分器[14]可实现此功能。传统SOGI-QSG的结构原理如图1所示。

传统SOGI-QSG传递函数为

式中：、分别为传统SOGI-QSG实现“等幅值、等相位”和“等幅值、90°移相”功能的传递函数；、分别为传统SOGI-QSG的输入信号及其“等幅值、等相位”的输出信号；wg为电网基波锁相频率，这里和下文将作为QSG的谐振频率；为增益系数。当时，传统SOGI-QSG的频率特性曲线如图2所示。

图3 INFC-SOGI-QSG的结构原理

INFC-SOGI-QSG的传递函数为

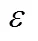
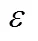
（c）不同下直流分量的跟踪性能对比

1.2 级联谐振滤波器

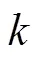
谐振滤波器在谐振点可以实现等幅值增益，先对特定阶次谐波进行提取，再通过负反馈消除对应的谐波扰动，并对其他谐波信号也有衰减效果。

单一谐振器的传递函数为

图5 级联型谐振滤波器的小信号模型

级联型谐振滤波器的频率特性曲线如图6所示，由式（11）结合图6可知，当谐波频率与谐振频率相同时，谐波消除模块对输入信号的谐振增益趋于零，因此对特定的奇次谐波具有良好的滤波效果，且不存在相位偏移。比例系数的取值为kr=1.414；理论上，wcn取值越小，滤波性能越强，对其他信号影响越小，但如果wcn的值过小，滤波器的响应速度就会降低，甚至影响谐振滤波器的衰减效果。为了降低谐振滤波器对频率波动的敏感度，截止频率的取值范围通常为30～90rad/s。

系统滤波响应时间s为

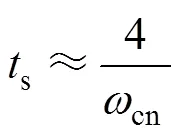
2 基于两相ab 静止坐标系下的锁相环控制策略

图7 ab PLL的锁相原理

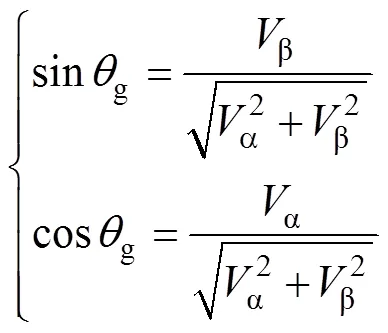
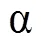
2.2 参数整定与性能分析

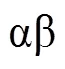
图8 改进型锁相结构

图9 ab PLL的线性化小信号模型

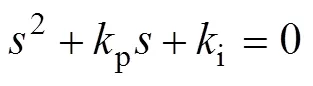
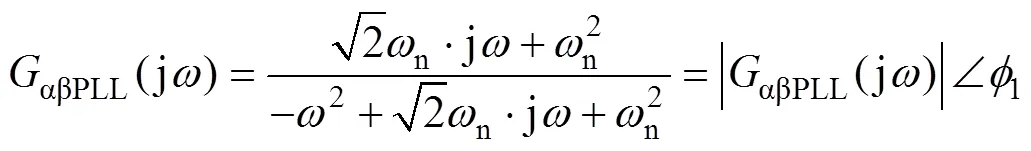
其中，有

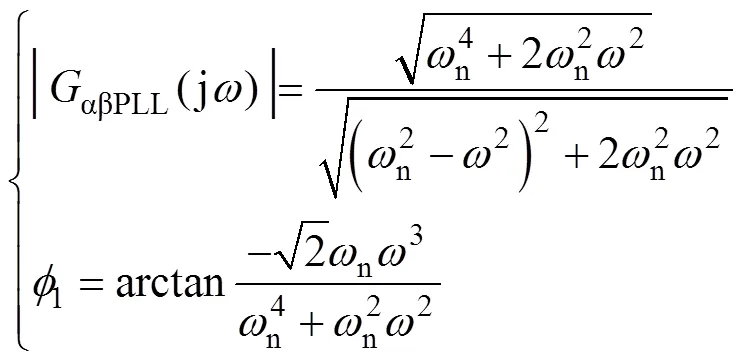
在经典的SRF-PLL结构的锁相内环添加低通滤波器（low-pass filter, LPF）是抑制谐波扰动的基本方法。因此，LPF-SRF-PLL的闭环传递函数为

图10 ab PLL的频率特性曲线

式中，1为在SRF-PLL锁相内环添加的LPF的时间常数。

根据式（20）可得LPF-SRF-PLL的频率特性曲线（1=0.02、p=0.5、i=10）如图11所示。

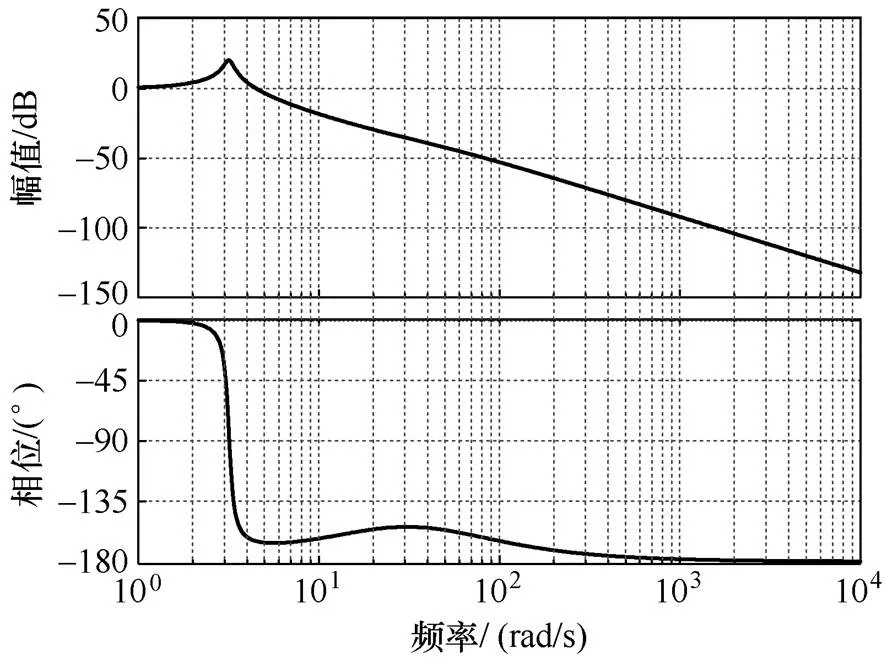
图11 LPF-SRF-PLL的频率特性曲线

3 仿真分析

3.1 三相不平衡

在仿真过程中，=2s时注入20%负序电压；为测试锁相结构的抗干扰能力，参考国家标准[17-18]给出的最恶劣情况模拟电网工况，同时注入4%的5、7次谐波，频率跳变为50.5Hz。三相电网电压不平衡工况的仿真结果如图12所示。

（a）三相不平衡电压

（b）相位误差

（c）频率响应

3.2 电压幅值跌落

为测试电压幅值跌落工况下的锁相性能，=2s时，仿真三相平衡电网的A相电压幅值突变，从311V跌落到0V；经过0.3s后，恢复到三相平衡状态，以此简单模拟低压故障穿越。电压幅值跌落工况的仿真结果如图13所示。

（a）A相电压幅值跌落

（b）相位误差

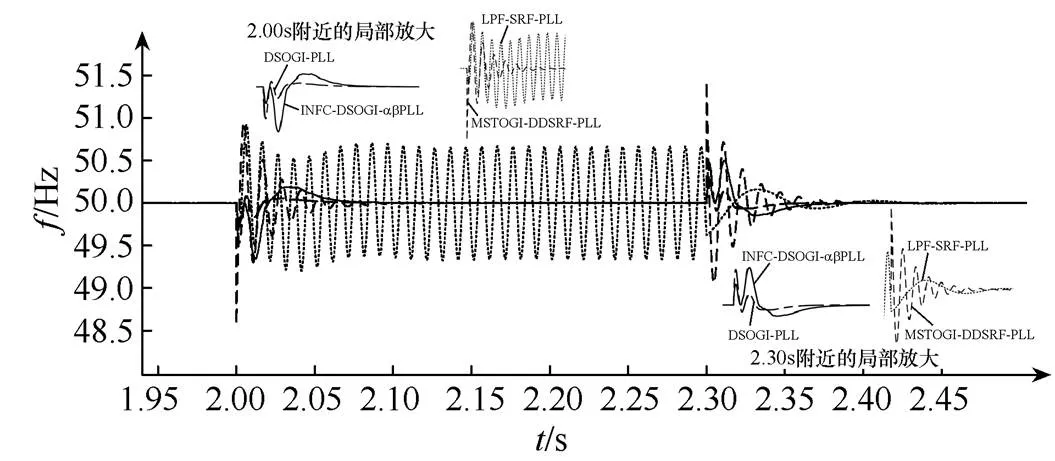
（c）频率响应

3.3 频率突变

为测试频率突变工况下的锁相性能，=2s时，仿真电网频率从50Hz跳变至47Hz。三相电网电压频率突变工况的仿真结果如图14所示。

（a）三相电网频率突变

（b）频率突变响应

图14 三相电网电压频率突变工况的仿真结果

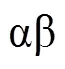
3.4 直流偏置

为测试直流偏置工况下的锁相性能，=2s时向电网C相电压注入15%的直流分量。三相电网电压直流偏置工况的仿真结果如图15所示。

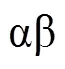
（a）三相电网直流偏置

（b）相位误差

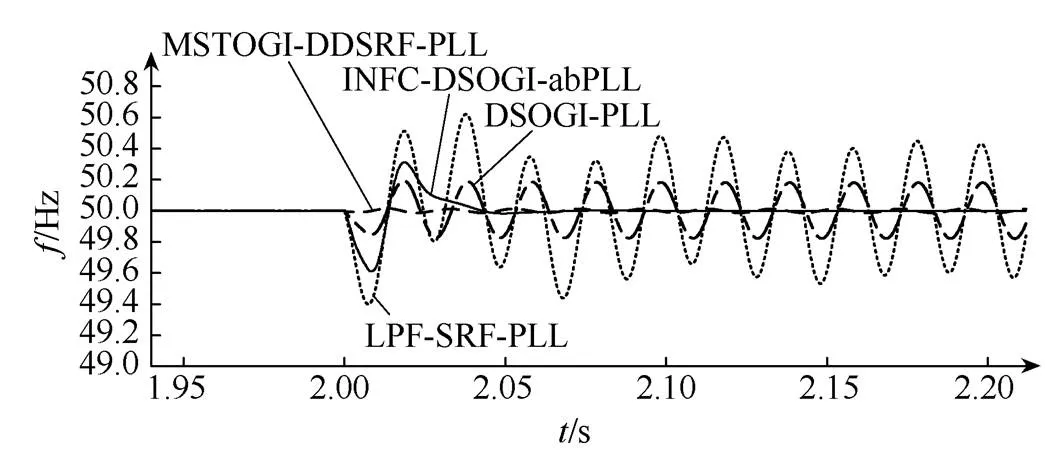
（c）频率响应

3.5 谐波畸变

为测试谐波畸变工况下的锁相性能，=2s时注入40%的负序电压、30%的5次谐波、25%的7次谐波、20%的11次谐波和15%的13次谐波。三相电网谐波畸变工况的仿真结果如图16所示。通过计算总谐波畸变率（total harmonic distortion, THD）验证INFC-DSOGI-PNSC结构的滤波效果。

（a）三相电网谐波畸变

（b）相位误差

（c）频率响应

3.6 相位突变

为测试相位突变工况下的锁相性能，=2s时，三相平衡电网电压相位突变增加90°。三相电网相位突变工况的仿真结果如图17所示。

（a）相位突变电压

（b）相位误差

（c）频率响应

4 结论

针对新能源电网环境下的复杂电网工况，本文提出一种在两相静止坐标系下基于改进型DSOGI的通用型锁相环控制策略，在锁相环的鉴相环节添加INFC-SOGI-QSG结构和级联谐振滤波策略，可以消除谐波分量和直流偏置的影响。与传统DSOGI- PLL、LPF-SRF-PLL的单一特性相比，改进型PLL在提升锁相内环系统带宽裕度的基础上实现了对电网相位的准确跟踪，工况通用性更强；与MSTOGI- DDSRF-PLL结构相比，具备更好的低次谐波滤除特性，可排除复杂工况下谐波扰动对相位误差的影响。通过软件仿真可知，当发生突变工况时，本文提出的改进型控制策略有较小的频率和相位误差超调、更快的系统响应速度，性能最佳。为了提高通用锁相环在复杂电网工况下的适应性，本文在锁相外环改进滤波结构，以此来提高锁相内环的系统性能。但是，目前在实际应用过程中，为了实现对电网正序分量相位的有效追踪，锁相环仍采用传统PI算法，因此为了使锁相环算法在能应对复杂电网工况的同时，还能适应日益革新的电能质量处理设备，尝试设计更加“智能”的控制器来使系统始终处于最优状态是十分必要的。

[1] 郭羿辰, 卢闻州. 基于改进型二阶广义积分器的锁相环研究[J]. 电气技术, 2022, 23(9): 14-18, 28.

[2] 张蕾. 一种适用于谐波电网环境的新型锁相环技术[J]. 电气技术, 2021, 22(8): 25-28, 44.

[3] 何宇, 漆汉宏, 罗琦, 等. 基于分数阶滤波器的三相锁相环技术[J]. 电工技术学报, 2019, 34(12): 2572- 2583.

[4] 祁永胜, 李凯, 高畅毓, 等. 三相电压不平衡下DDSRF-PLL与DSOGI-PLL的锁相误差检测与补偿方法[J]. 电工技术学报, 2024, 39(2): 567-579.

[5] 洪小圆, 吕征宇. 基于同步参考坐标系的三相数字锁相环[J]. 电工技术学报, 2012, 27(11): 203-210.

[6] GOLESTAN S, GUERRERO J M, VASQUEZ J C, et al. A study on three-phase FLLs[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 213-224.

[7] 唐爱博, 王安娜, 宋崇辉. 基于改进SOGI-PLL电网基波正序分量同步方法[J]. 控制工程, 2021, 28(6): 1136-1142.

[8] 李志华, 高岚. 船舶电网改进型DDSRF-PLL相位跟踪方法研究[J]. 中国修船, 2022, 35(6): 48-52.

[9] JAALAM N, RAHIM N A, BAKER A H, et al．A comprehensive review of synchronization methods for grid-connected converters of renewable energy source[J]. Renewable and Sustainable Energy Reviews, 2016, 59: 1471-1484.

[10] 高正中, 王亚男, 牛慧晖, 等. 用于矿井电网电压同步频率检测的改进型DSOGI-PLL[J]. 工矿自动化, 2020, 46(8): 75-81.

[11] 回楠木, 王大志, 李云路. 基于复变陷波器的并网锁相环直流偏移消除方法[J]. 电工技术学报, 2018, 33(24): 5897-5906.

[12] 回楠木, 王大志, 李云路. 复杂电网下基于双改进型SOGI的三相并网锁相环[J]. 仪器仪表学报, 2018, 39(4): 123-132.

[13] 张会来. 电网不平衡条件下频率自适应MAF锁相方法研究[D]. 青岛: 青岛科技大学, 2021.

[14] 郭羿辰, 卢闻州. 基于改进型二阶广义积分器的锁相环研究[J]. 电气技术, 2022, 23(9): 14-18, 28.

[15] 江燕兴, 潘逸菎, 窦伟. 一种用于光伏并网逆变器的高性能锁相环设计[J]. 电工电能新技术, 2016, 35(7): 75-80.

[16] 杨旭红, 郝鹏飞, 姚凤军, 等. 一种改进的锁相环用于抑制三相不平衡和直流偏移[J]. 科学技术与工程, 2020, 20(33): 13705-13711.

[17] 电能质量 电力系统频率偏差: GB/T 15945—2008[S]. 北京: 中国标准出版社, 2008.

[18] 电能质量 公用电网谐波: GB/T 14549—93[S]. 北京: 中国标准出版社, 1993.

Phase-locked loop control strategy based on improved dual second-order generalized integrator in two-phase stationary coordinate system

HAN Yixin1ZOU Fumin1HOU Jun2ZHANG Qing2

(1.School of Electronic, Electrical Engineering and Physics, Fujian University of Technology, Fuzhou 350118; 2. Fujian Xingyun Electronics Co., Ltd, Fuzhou 350000)

Due to the widespread integration of distributed renewable energy sources and diverse load into the power grid, the conventional synchronous reference frame-phase-locked loop (SRF-PLL) structure fails to accurately track grid parameters such as phase and frequency under complex grid conditions. Therefore, this paper proposes a novel phase-locked loop control strategy based on an improved double second-order generalized integrator (DSOGI) in the two-phase stationary coordinate system. Firstly, a cascaded resonant filter is employed to address odd harmonics in the low-frequency range. Additionally, a DC bias filter branch is incorporated based on second-order generalized integrator quadrature signal generator (SOGI-QSG) to mitigate DC disturbances, achieve decoupled separation of positive and negative sequence voltages, and optimize suppression of high-frequency harmonics. Subsequently, aabphase-locked loop (PLL) structure is constructed to enhance dynamic response performance by leveraging the small signal control model and improve phase-locking accuracy. Finally, the efficacy of the enhanced phase-locked loop control strategy is validated through comparative simulation using Matlab/Simulink.

second-order generalized integrator quadrature signal generator (SOGI-QSG); phase-locked loop (PLL); DC bias; cascaded resonant filter

2023-08-30

2023-10-23

韩以鑫（1998—），男，江苏盐城人，硕士研究生，主要研究方向为储能控制技术。