基于响应曲面中心组合设计的介质阻挡负载特征参数分析与优化
陈勇权 唐雄民 李仲涛
基于响应曲面中心组合设计的介质阻挡负载特征参数分析与优化
陈勇权 唐雄民 李仲涛
(广东工业大学自动化学院,广州 510006)
为了充分发挥介质阻挡放电(DBD)负载的性能,以高频脉冲激励作为介质阻挡负载的激励波形,以第一次放电时的负载电流幅值作为优化目标。基于响应曲面法中心组合设计建立数学模型,分析介质阻挡层厚度、脉冲电压幅值、脉冲升降沿时间和相对介电常数4个因素对高频脉冲激励下DBD负载第一次放电时负载电流幅值的影响,优化介质阻挡负载特征参数。结果表明,对DBD负载电流的影响强度从大到小依次为介质阻挡层厚度、脉冲电压幅值、脉冲升降沿时间、相对介电常数。在本文设定条件下,负载电流幅值的最大值8.692A在脉冲升降沿时间为200ns、脉冲电压幅值为4kV、介质阻挡层厚度为1mm、相对介电常数为8时获得。
介质阻挡放电(DBD);响应曲面法;负载电流幅值;有限元方法;优化
0 引言
介质阻挡放电(dielectric barrier discharge, DBD)是绝缘介质插入放电空间的一种非平衡态气体放电,又称介质阻挡电晕放电或无声放电。工业中常用的一种DBD负载的典型结构如图1所示,DBD负载一般由高压电极、介质阻挡层、气隙和低压电极组成。当放电电极间施加足够高的激励电压时,电极间的气体会被击穿而在微放电通道中发生放电现象,进而产生大量的活性粒子。由于这一特性,DBD技术在现阶段已广泛应用于材料表面处 理[1]、空气净化与水处理[2]、紫外光生成[3]和臭氧合成[4]等工业领域。
为了能充分发挥DBD负载的性能,国内外相关工作者做了大量实验研究工作。例如,等以DBD型臭氧发生器为例,分析输入电压、气体流量和反应室尺寸等参数变化对臭氧生产速率的影响[5];等从发光长度、放电电流、消耗功率和能量及发射光谱等方面分析比较纳秒脉冲和微秒脉冲驱动对产生氦气的影响[6];和通过在相同条件下分别施加短脉冲及长脉冲激励在电极板间产生氩气DBD,并在此基础上分析和讨论不同的升降沿时间对放电特性的影响[7]。这些实验结果表明[8-13],脉冲电压幅值、脉冲升降沿时间、介质阻挡层厚度、相对介电常数是影响DBD负载性能的4个主要因素。然而,传统实验研究方法无法获得DBD负载性能与这4种因素的内在关系,也无法获知这4种因素对DBD负载性能影响程度的强弱关系,这使科研工作者很难对DBD负载的供电电源和DBD负载参数进行进一步优化。针对这一现状,本文通过COMSOL Multiphysics[14]仿真软件建立DBD负载一维流体模型来分析介质阻挡层厚度、脉冲电压幅值、脉冲升降沿时间和相对介电常数这4种主要因素对DBD负载性能的影响。此外,本文还利用单因素试验及响应面试验对DBD负载性能进行优化,以期能充分发挥DBD负载的性能,为工业优化DBD负载性能提供理论基础。
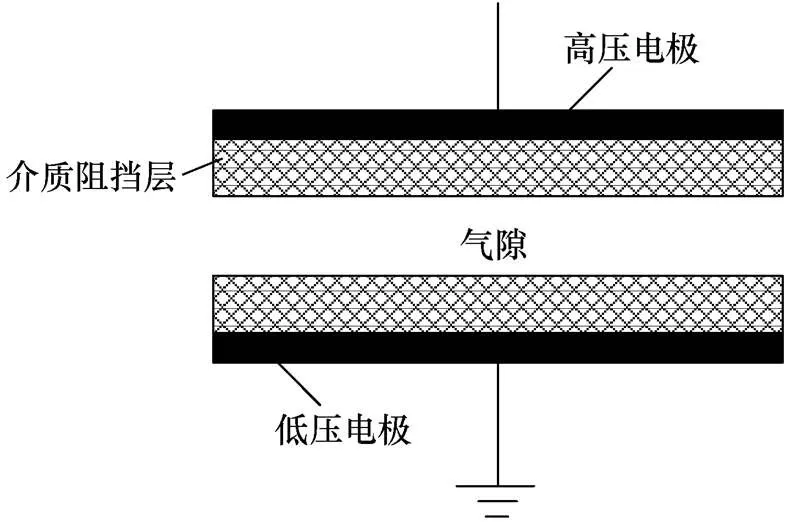
图1 一种DBD负载典型结构
1 DBD负载的一维流体模型
1.1 控制方程和边界条件方程
DBD负载的一维流体模型主要由控制方程及其边界条件构成,其中控制方程主要包括电子连续性方程、电子能量连续性方程、重物质的输运方程、放电区域的静电场泊松方程,具体表达为

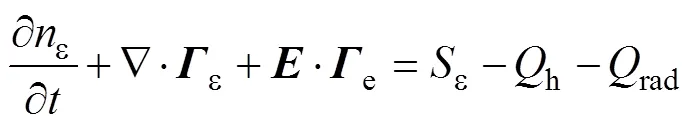


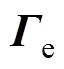
边界条件包括阻挡介质层表面的电子通量的边界条件、电极表面的电子能量的边界条件、重物质的边界条件、表面电荷积累的边界条件。这些边界条件的表达式为

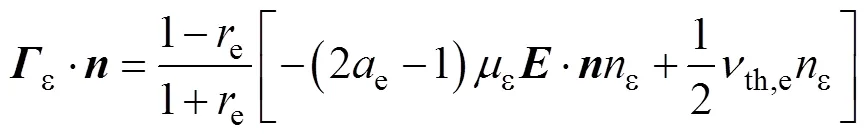
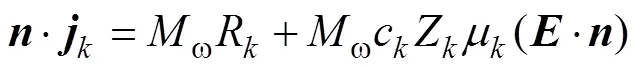
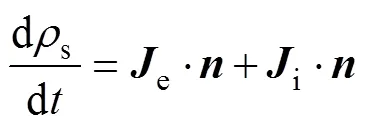
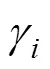
考虑到DBD负载在放电过程中,电极的直径远大于气隙宽度,因此可采用一维流体模型来进行简化计算[15]。基于式(1)~式(8)给出的控制方程及边界条件,可搭建如图2所示的DBD负载一维流体模型,并以此为基础来分析DBD负载的特性。图2中,d为介质层厚度,g为气隙宽度。不失一般性地,本文采用图3所示的脉冲激励波形。在图3中,为激励周期,r为上升沿时间,f为下降沿时间,w为激励脉宽,m为激励幅值。

图2 DBD负载一维流体模型
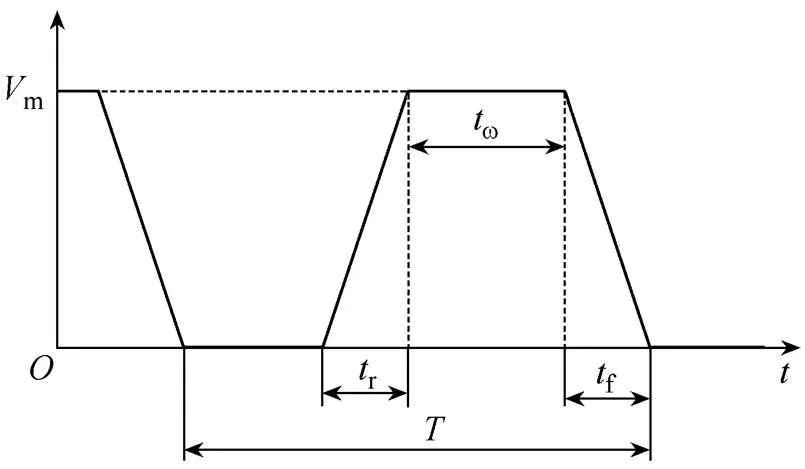
图3 脉冲激励波形
1.2 反应气体的化学设定
考虑到气体放电的相似性[16],选择氩气(Ar)这种经典的工作气体作为DBD负载填充气体,并选取7种放电间隙的主要反应、2种表面反应[17],4种不同类型的粒子(电子e、氩气的气体分子Ar、氩气的激发态粒子Ars、带正电的氩离子Ar+)来描述DBD负载的放电过程。主要粒子的化学反应方程见表1。

表1 主要粒子的化学反应方程
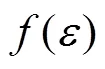
2 多因素影响强度
2.1 流体模型结果
一般情况下,DBD负载第一次放电电流幅值与DBD负载性能密切相关[20],因此本文选择用DBD负载第一次放电电流幅值来描述DBD负载性能。为了研究DBD负载性能与前面所述4种因素的关系,利用Box-Behnken设计方法设计一个4因素3水平的仿真实验:脉冲的升降沿时间取值为200ns、300ns、400ns,外加激励的脉冲电压幅值取值为2kV、3kV、4kV,介质阻挡层厚度取值为1mm、2mm、3mm,相对介电常数取值为7、7.5、8。用、、、分别表示脉冲的升降沿时间、脉冲电压幅值、介质阻挡层厚度、相对介电常数,这4个自变量的强度编码见表2,其中-1、0和1分别代表低、中和高实验水平。通过改变这4个因素的实验水平进行实验设计,得到对应的实验结果见表3。表3中为DBD负载第一次放电电流的幅值。

表2 4个自变量的强度编码
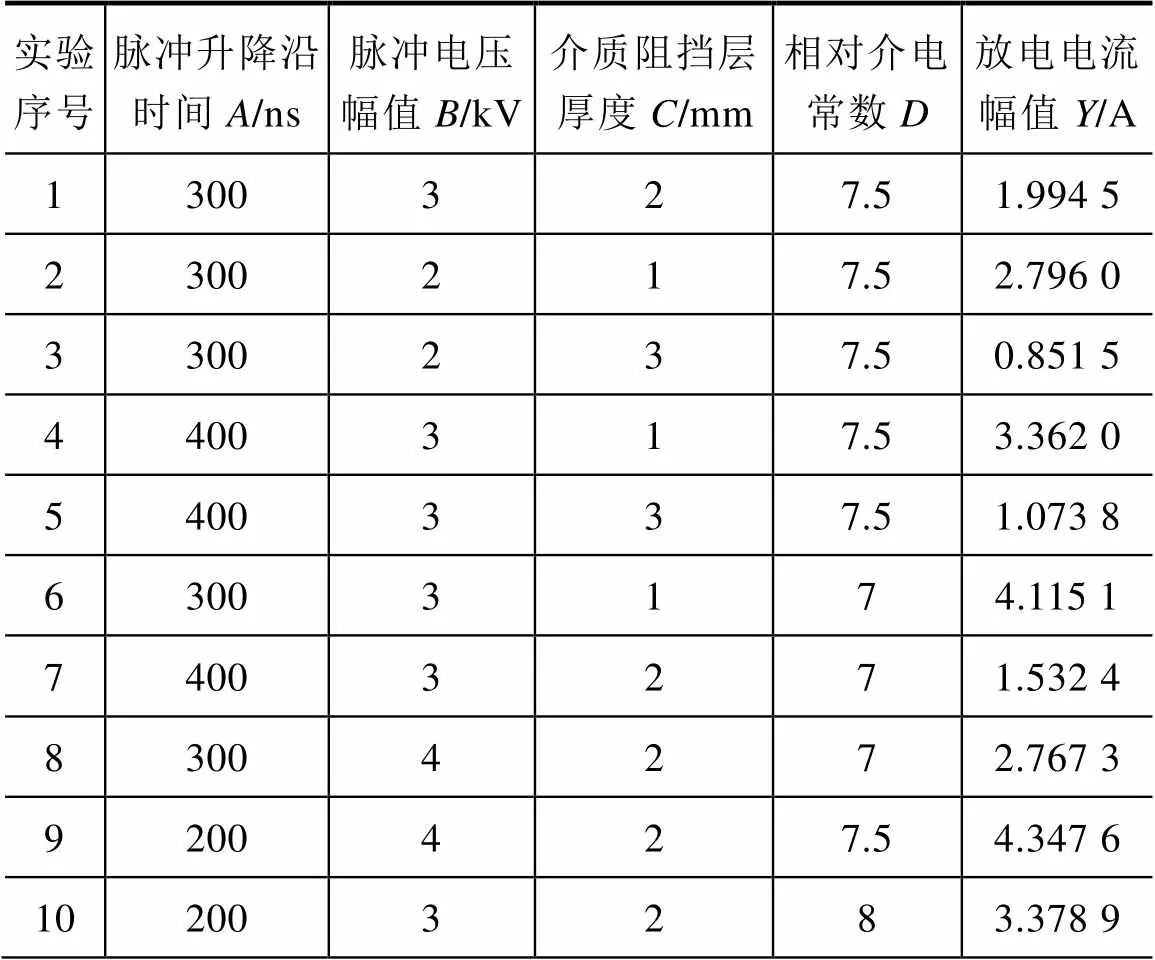
表3 实验结果

(续表3)
2.2 单因素响应分析
图4为脉冲升降沿时间、脉冲电压幅值、介质阻挡层厚度及相对介电常数对气体第一次放电电流幅值影响的单因素响应曲线。图4是由依次固定其中3个量在零水平的情况下,记录剩下的一个自变量对气体电流幅值的影响而生成的。从图4可以看出,、、、这4个单因素在图示取值区间内对响应变量变化趋势的影响几乎是线性的。此外,从各个曲线的陡峭程度还能看出,介质阻挡层厚度对响应变量的影响极其显著,脉冲电压幅值次之,相对介电常数对响应变量的影响则最小。

图4 单因素响应曲线
2.3 DBD负载的线性方程
在Box-Behnken实验设计基础上,根据DBD负载输出变量与输入变量之间的关系,可拟合出一个由二次多元回归线性方程表示的经验关系,即
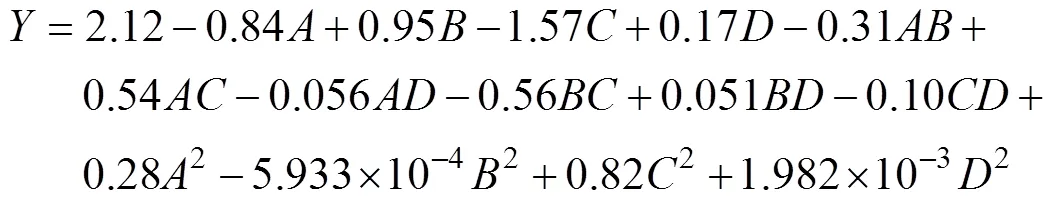
式(9)中,各项系数的正负表示该项因素对响应结果的影响方向,而系数的绝对值大小则反映该项对响应结果影响的大小。通过式(9)可获得介质阻挡负载第一次放电电流幅值的预测值,预测值与实际值的关系如图5所示。
从图5可以看出,所获得的预测值与Box-Behnken实验设计所得到的实际值非常接近,二者关系的拟合曲线近似一条直线,这表明该模型能成功捕捉过程变量对响应的相关性。
采用帕雷托方差分析法[21],可以得到DBD负载输入-输出模型的方差见表4。从表4可以看出,表示整个回归方程是否显著的值为117.260,且无显著影响的概率值为<0.000 1,远小于一般模型显著性检验规定的<0.05,此结果表明二次多元回归线性方程与各因素的拟合效果极好,只有0.01%的概率模型不显著。此外,从表4中各因素的值可知,、、、、、2这几项对响应变量的影响是极为显著的(<0.000 1),且根据各个因素的值,4个主要因素的影响强度从大到小依次为介质阻挡层厚度、脉冲电压幅值、脉冲升降沿时间、相对介电常数。
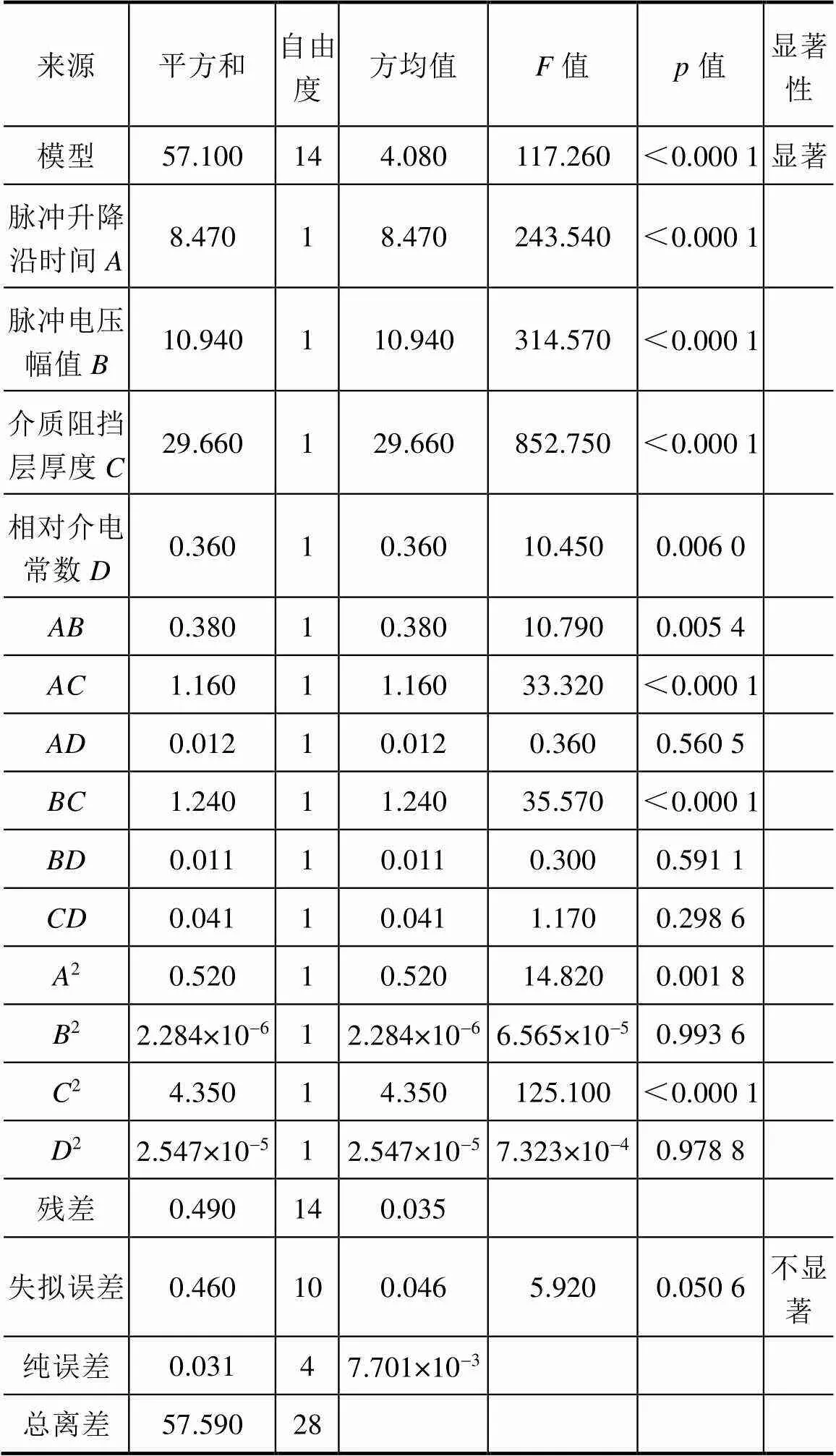
表4 DBD负载输入-输出模型的方差

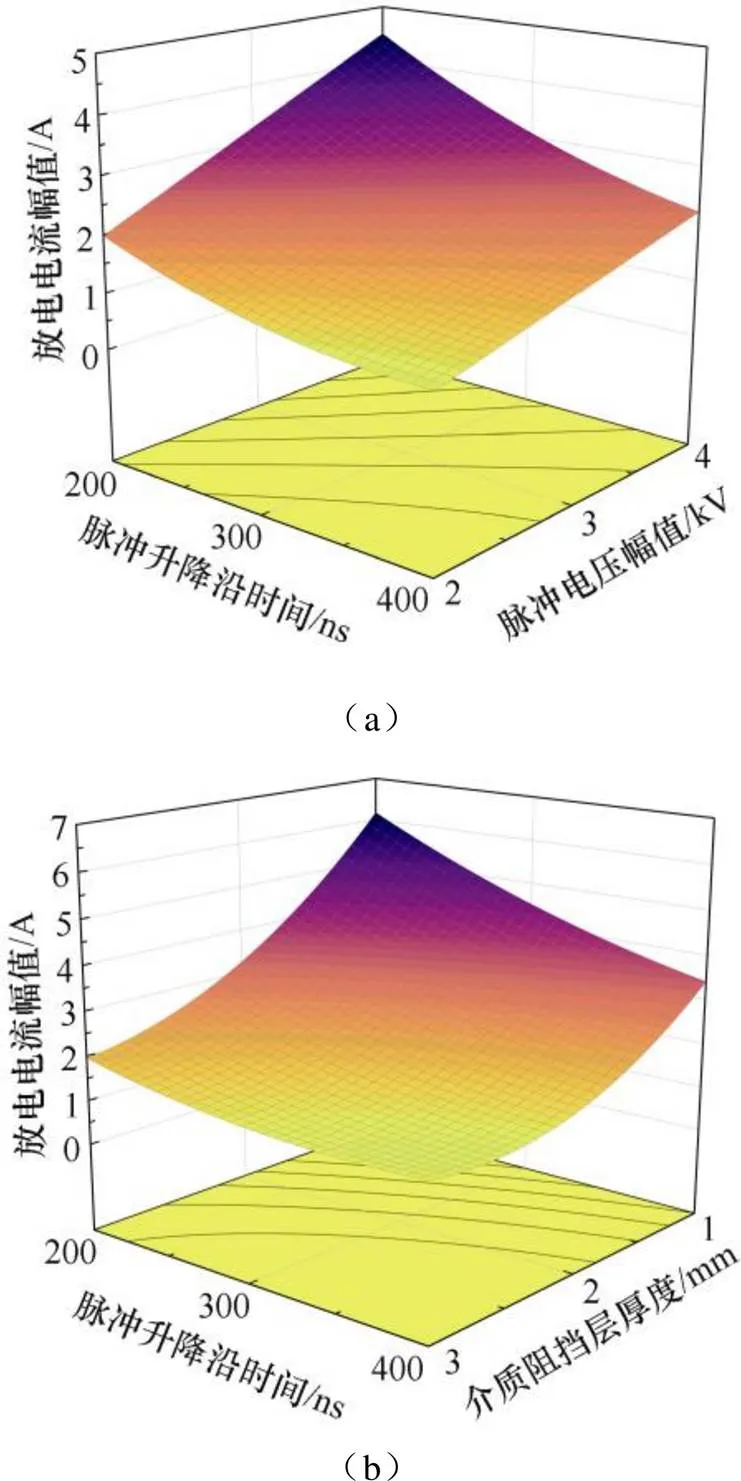
根据图6所示结果,可求得最佳实验条件为:脉冲升降沿时间为200ns、脉冲电压幅值为4kV、介质阻挡层厚度为1mm、相对介电常数为8。在此条件下,根据本文一维流体模型求得的介质阻挡负载第一次放电电流幅值最大值为8.692A,与回归模型的预测值8.75A基本吻合,证明了该模型的准确性和良好的拟合精度。
3 结论
本文基于DBD负载的控制方程及其边界方程构建了一维流体数值模型,并通过该模型分析了脉冲升降沿时间、脉冲电压幅值、介质阻挡层厚度、相对介电常数这4个主要因素对DBD负载性能的影响强度,同时分析了这4个主要因素之间交互作用的影响顺序,最后得到在脉冲升降沿时间为200ns、脉冲电压幅值为4kV、介质阻挡层厚度为1mm、相对介电常数为8的条件下,DBD负载将获得最佳性能。实验结果表明,这4种因素对DBD负载电流的影响强度从大到小依次为介质阻挡层厚度、脉冲电压幅值、脉冲升降沿时间、相对介电常数。
[1] 黑雪婷, 高远, 窦立广, 等. 纳秒脉冲介质阻挡放电等离子体驱动CH4-CH3OH转化制备液态化学品的特性研究[J]. 电工技术学报, 2022, 37(15): 3941- 3950.
[2] 武海霞, 陈卫刚, 张微薇, 等. 介质阻挡放电处理水中有机污染物研究进展[J]. 水处理技术, 2018, 44(11): 19-25.
[3] 肖俊, 陈荣, 雷宇, 等. 介质阻挡放电诱发185nm紫外光结合Bi2WO6/NMO催化降解CS2[J]. 合肥工业大学学报(自然科学版), 2019, 42(10): 1404-1410.
[4] 商克峰, 王美威, 鲁娜, 等. 沿面/体介质阻挡放电装置的放电及臭氧生成特性[J]. 高电压技术, 2021, 47(1): 353-359.
[5] BUNTAT Z, SMITH I R, RAZALI N M. Ozone generation using atmospheric pressure glow discharge in air[J]. Journal of Physics D: Applied Physics, 2009, 42(23): 235202.
[6] ZHANG Cheng, SHAO Tao, WANG Ruixue, et al. A comparison between characteristics of atmospheric- pressure plasma jets sustained by nanosecond- and microsecond-pulse generators in helium[J]. Physics of Plasmas, 2014, 21(10): 103505.
[7] LEIWEKE R J, GANGULY B N. Effects of pulsed- excitation applied voltage rise time on argon metastable production efficiency in a high pressure dielectric barrier discharge[J]. Applied Physics Letters, 2007, 90(24): 241501.
[8] HENRY RIGIT A R, ALI I, BOON T C, et al. Effect of number of electrodes on electrical performance of surface dielectric barrier discharge plasma actuator[C]// 2020 13th International UNIMAS Engineering Con- ference (EnCon), Kota Samarahan, Malaysia, 2020: 1-4.
[9] GANEA I, MORAR R. Factors that increase the electric field of the dielectric barrier ozone gen- erators[J]. IOP Conference Series: Materials Science and Engineering, 2017, 200: 012057.
[10] PAN Mingqiang, YAO Furong, LIU Jizhu, et al. Effect of magnetic field on activation performance of silicon/glass dielectric barrier discharge[C]//2018 19th International Conference on Electronic Packaging Technology (ICEPT), Shanghai, China, 2018: 908-912.
[11] XIE Qing, GAN Wenyan, ZHANG Cheng, et al. Effect of rise time on nanosecond pulsed surface dielectric barrier discharge actuator[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(2): 346-352.
[12] WANG Tahan, LIU Wenzheng, HE Kun, et al. Effects of different materials on dielectric barrier discharge characteristic[C]//2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 2020: 1-4.
[13] XU Yonggang, JIANG Weiman, TANG Jie, et al. Influence of driving frequency on the argon dielectric barrier discharge excited by Gaussian voltage at atmospheric pressure[J]. IEEE Transactions on Plasma Science, 2016, 44(11): 2553-2563.
[14] 张泽权, 蔡新景. 基于COMSOL仿真的电力电缆局部放电检测传感器设计[J]. 电气技术, 2023, 24(4): 29-36.
[15] 张增辉, 邵先军, 张冠军, 等. 大气压氩气介质阻挡辉光放电的一维仿真研究[J]. 物理学报, 2012, 61(4): 291-298.
[16] 车瑞, 孙明. 基于有限元法的气体放电模拟综述[J]. 电气技术, 2022, 23(7): 18-25, 80.
[17] PAN Jie, TAN Zhenyu, WANG Xiaolong, et al. Comparative study of pulsed dielectric barrier discharges in argon and nitrogen at atmospheric pressure[J]. IEEE Transactions on Plasma Science, 2015, 43(2): 557-566.
[18] HAGELAAR G M, PITCHFORD L C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models[J]. Plasma Sources Science and Technology, 2005, 14(4): 722-733.
[19] YAO Congwei, CHANG Zhengshi, MU Haibao, et al. Two-dimension simulation of small scale dielectric barrier discharge in argon[C]//2015 IEEE 11th Inter- national Conference on the Properties and Applications of Dielectric Materials (ICPADM), Sydney, NSW, Australia, 2015: 384-387.
[20] LIU Shuhai, NEIGER M. Excitation of dielectric barrier discharges by unipolar submicrosecond square pulses[J]. Journal of Physics D: Applied Physics 2001, 34(11): 1632-1638.
[21] MEHANAOUI A, LAROUSSI T, MEZACHE A. New Pareto clutter parameters estimators based on log- moments and fractional negative-moments[C]//2017 Seminar on Detection Systems Architectures and Technologies (DAT), Algiers, Algeria, 2017: 1-5.
Analysis and optimization of dielectric barrier load characteristic parameters based on response surface center combination design
CHEN Yongquan TANG Xiongmin LI Zhongtao
(School of Automation, Guangdong University of Technology, Guangzhou 510006)
To take advantage of the potential of dielectric barrier discharge (DBD) load, a high-frequency pulse excitation is selected as the excitation waveforms and the load current amplitude of the first discharge as the optimization objective. Based on the method of response surface center combination design, a mathematical model is built to analyze the effects of dielectric barrier layer thickness, applied voltage amplitude, applied voltage rising and falling time and the relative permittivity on the load current amplitude of the first discharge, optimizing the characteristic parameters of dielectric barrier discharge load. The results show that the influence on the DBD load current is in descending order of dielectric barrier layer, applied voltage amplitude, applied voltage rising and falling time, the relative permittivity. Under these conditions, the maximum load current amplitude is 8.692A when the applied voltage rising and falling time is 200ns, the applied voltage amplitude is 4kV, the thickness of dielectric barrier layer is 1mm and the relative permittivity is 8.
dielectric barrier discharge (DBD); response surface methodology; load current amplitude; the finite element method; optimization
国家自然科学基金项目(51207026)
2023-10-09
2023-11-14
陈勇权(1999—),男,硕士研究生,主要研究方向为介质阻挡放电机理分析及其供电电源设计。

