基于改进A*-DWA算法的移动机器人路径规划

刘钰铭,黄海松,2+,范青松,朱云伟,陈星燃,韩正功

(1.贵州大学 现代制造技术教育部重点实验室,贵州 贵阳 550025;2.重庆机电职业技术大学 信息工程学院,重庆 402760)

0 引言

机器人移动作业过程中,能源容量的多少从根本上决定了其执行给定任务的持久性,目前主要通过增加能源容量与补给次数完成,但提升效果有限且增加了资源成本[1]。在能源携带有限、补给不及时的情况下,机器人可通过节能、有效的路径规划方法,减少能源的损耗,提升复杂环境下的作业能力[2]。

常见的路径规划方法有遗传算法[3]、A*算法[4]、快速随机树搜索法[5]、动态窗口法[6](Dynamic Window Approach,DWA)、人工势场法[7]等,其中A*算法应用最广泛。劳彩莲等[8]改进A*算法的选取策略,消除多余转折点,生成平滑路径。LIN等[9]在A*的启发函数引入父节点信息并改变权重,减少搜索的节点数量与时间。然而,上述方法规划的路径非节能路径。在节能路径规划的相关研究中,张浩杰等[2]基于改进实时动态A*(Anytime Dynamic A*,AD*)算法对路径规划的能耗和效率方面进行改进,但其路径不平滑,不利于机器人运动平稳性。LIU等[10]提出基于距离—能耗搜索准则的A*算法规划节能路径,但路径存在冗余转折点,未考虑频繁转弯带来额外能量的损耗。PAL等[11]提出高效节能A*(Energy efficient A*,EA*)算法,通过减少移动机器人转弯次数降低能量损耗,但仅考虑转弯时的能量消耗,没考虑地面摩擦等环境因素对节能路径规划的影响,不足以规划出能耗最优路径。LIU等[12]考虑地面摩擦,在A*的成本函数中引入基于能量邻接矩阵搜索节能路径,并对路径进行平滑处理进一步降低能耗,但只适用于平坦路面环境下的节能规划。在上述能耗研究中,所构建的能耗模型没能全面考虑地面摩擦、坡道等环境因素对节能路径规划的影响,也未能考虑规划路径不平滑、多转折、转折角度大造成的能量损耗,且上述方法只适用于静态环境下的路径规划,不具备动态环境下的避障能力。

DWA算法具备动态环境下的避障能力,但易陷入局部解。为此,学者们将A*算法与DWA融合,ZHU等[13]构建了全局最优路径评价函数,将A*算法与DWA融合,避免陷入局部解的同时保持路径全局最优。邹文等[14]建立拓扑层地图来删除A*的冗余节点提高路径平滑度,同时为机器人增加运动状态优化DWA,将两者融合提升路径规划效率的同时增强动态环境下的灵活性。王彬等[15]将基于启发函数权重可动态调节的改进A*算法与基于环境自适应改进策略的动态窗口法相融合,不但解决了传统 A*和DWA冗余点多、效率低、路径冗余等问题,而且提高了路径安全性和实时性,更符合移动机器人的运动特性。

上述方法从不同角度对A*算法与DWA进行了改进,但都没考虑复杂狭窄环境下机器人节能路径的规划与动态避障。为此,本文提出一种节能A*算法(Energy-Saving A*algorithm,ESA*)与改进DWA算法(Improved DWA algorithm,IDWA)相融合的路径规划方法。基于地面摩擦、坡度、载重量等关键因素,构建出机器人能耗模型,提出以能耗成本为搜索新准则的ESA*算法规划节能路径,同时通过动态基准转弯惩罚和三角剪枝法避免因冗余路径、转折点产生额外能量损耗并利用弦定弧过渡法对路径平滑处理得到光滑、连续的全局节能路径。在此基础上融合改进DWA并提出航向角自适应调整策略对融合算法进行优化,提升机器人在复杂、狭窄环境下的动态避障能力,与此同时,设计全局节能路径偏离评价与能耗评价子函数进行局部能耗最优路径轨迹规划。

1 算法简述

1.1 传统A*算法

A*算法常用于静态环境下最优路径的求解,其根据代价函数在静态环境下选择一条从起点到终点距离最优的路径。传统A*算法的代价函数如下:

f(n)=g(n)+h(n)。

(1)

式中:g(n)表示起点到节点n的实际距离代价,h(n)表示节点n到目标点的预估距离代价。距离代价采用欧式距离来进行计算,如式(2)所示:

h(n)=sqrt[(xgoal-xn)2+(ygoal-yn)2],

g(n)=sqrt[(xn-xstart)2+(yn-ystart)2]。

(2)

其中(xn,xn)、(xstart,ystart)、(xgoal,ygoal)分别表示节点n、起点start、终点goal的坐标;

1.2 传统DWA算法

DWA算法通过机器人运动学模型对其速度约束空间进行采样,模拟机器人预测时间内的运动轨迹,再利用评价函数在多组运动轨迹中择选出评分最优的轨迹。机器人的运动学模型为:

θt=θt-1+ω(t)Δt。

(3)

其中:x(t)、y(t)、θt为机器人t时刻的位姿信息;x(t-1)、y(t-1)、θt-1为t-1时刻的位姿信息。DWA对模拟出机器人的若干运动轨迹进行评估择优,其评估函数为:

G(v,ω)=σ[αhead(v,ω)+βdist(v,ω)+γvel(v,ω)]。

(4)

式中:head(v,ω)、dist(v,ω)、vel(v,ω)分别为方位角、距离、速度评价子函数;σ为平滑函数;α、β、γ为各评价子函数的加权系数。

2 结合ESA*和IDWA的路径规划方法

2.1 ESA*算法

2.1.1 基于能耗成本的搜索准则

移动机器人的能量耗损主要为电子设备工作消耗的能量Eequipment和运动过程中所消耗的能量Emotion[16]。移动机器人的总能耗方程如下:

Erobot=Eequipment+Emotion=

(5)

式中:Pmotion为运动过程中的功率耗损,Pequipment为机器人电子设备的功率耗损。

由图1所示移动机器人运动过程的受力情况可知,移动机器人在运动过程中克服牵引阻力所损耗的能量为:

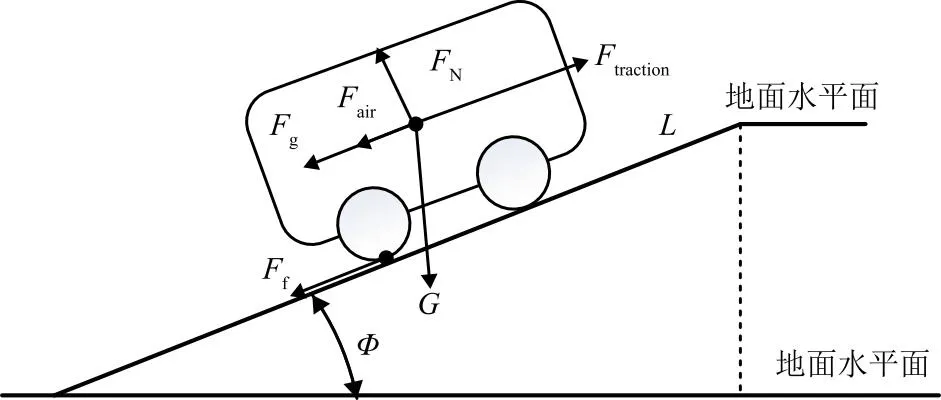
图1 移动机器人运动过程的受力情况

W=Pmotion×Δt=Ftraction×Δs=

(Ff+Fair+Fg)×L。

(6)

式中:W为运动过程的总功;Ftraction为运动过程的总牵引力;Ff、Fair、Fg为运动过程中的摩擦力、空气阻力以及重力斜面水平分力;L为移动距离;移动机器人在运动过程始终保持匀速行驶且速度低。因此,由式(5)和式(6)可知机器人在运动过程中的总能耗

Erobot=1+k[mgsin(φ)×s+μmgcos(φ)×s]。

(7)

为了表征复杂环境下机器人的移动距离和能量消耗,MEJRI等[17]构建了基于距离的邻接矩阵AD与基于能量的邻接矩阵AE。本文以能量矩阵AE(i,j)为ESA*算法的搜索准则:

AE(i,j)=Erobot=1+k[sin(φ)+

μi,jcos(φ)]mgAD(i,j)。

(8)

其中:μi,j为位置i到位置j的平均摩擦系数;考虑现实坡度对机器人移动的能耗影响,提出基于地面水平的邻接矩阵Aφ(i,j),如图2所示,具体公式如下:

图2 基于地面水平的邻接矩阵Aφ

Aφ(i,j)=φj-φi。

(9)

其中:Aφ(i,j)表示位置i到位置j的坡度大小以及坡度状态,相邻位置i与j数值差的绝对值表示对应区域间的坡度,正负表示移动机器人爬坡与下坡两种状态。结合式(1)、式(8)和式(9)可得基于能耗成本的路径搜索新准则:

E(k)=g′(k-1)+AE(k-1,k)+AE(k,goal)。

(10)

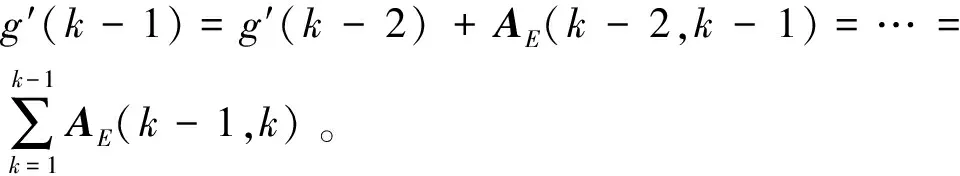
2.1.2 转折惩罚与剪枝

为解决ESA*算法因冗余节点多、路径多转折、转折角度大带来额外能量耗损的问题,本文提出两阶段优化方法。一阶段在节点扩展中引入基于动态转角基准的转弯惩罚因子避免转折点的产生,先由父节点与当前节点的坐标关系确定机器人的移动方向并以移动方向为转角基准,如图3所示;然后根据扩展节点与转角基准的位置关系,在能耗评价函数中利用转弯惩罚因子对其惩罚处理。引入惩罚因子的能耗评价函数为:

图3 动态转角基准示意图

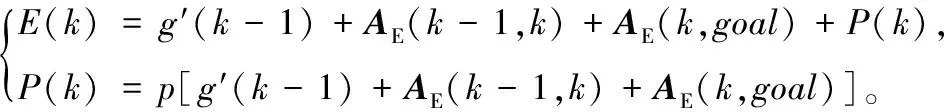
(11)

二阶段为了减少冗余路径、路径转折角度大造成的能量损耗,对初始规划路径节点进行三角剪枝处理,其通过表1算法实现。该方法示意图如图4所示。

表1 三角剪枝处理

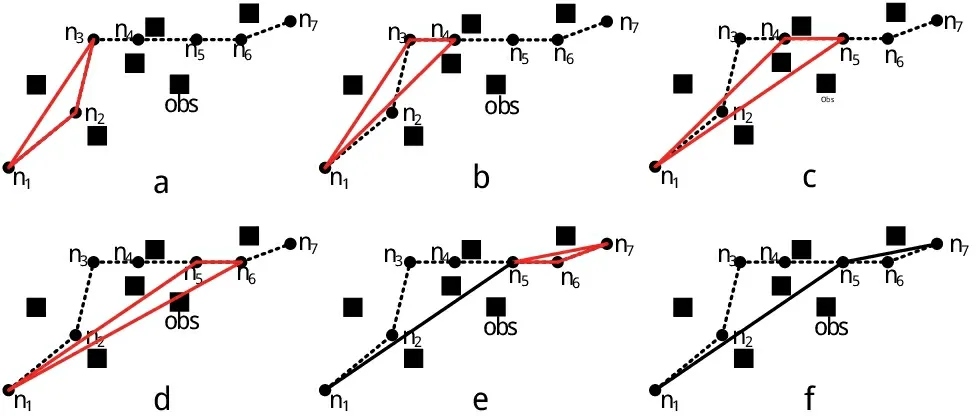
图4 路径三角剪枝示意图

2.1.3 基于动态弦定弧过渡的路径平滑处理方法

针对路径出现的急转折或角转折造成机器人能量损耗,影响机器人运行的平稳性和作业的持久性,本文通过表2算法对转折点进行平滑处理,得到光滑连续、低耗能的路径。平滑处理示意图如图5所示。

表2 转折平滑处理

图5 路径转折平滑处理示意图

2.2 IDWA算法

传统DWA局部路径规划时,没有考虑路径轨迹所消耗的能量,最优的轨迹不一定是能耗损耗少的。为此,设计能耗评价子函数,对局部路径轨迹进行能耗评价。RIAZI等[18]将加速度与速度的乘积定义为伪功率,伪功率的减少能有效降低能耗与峰值功率。设计的能耗评价子函数为:

(12)

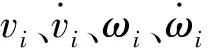
G(v,ω)=σ[αhead(v,ω)+βdist(v,ω)+

γvel(v,ω)+δEnergy(v,ω)]。

(13)

其中δ为能耗评价子函数的加权系数。

3 窄空间下融合ESA*和IDWA算法的路径优化方法

ESA*算法在静态环境下能规划出光滑连续的全局节能路径,但在狭窄、动态的环境下面对移动障碍物往往不能及时躲避,发生碰撞;IDWA算法能在动态环境中成功躲避障碍物,但易陷入局部解。为此,将两者进行融合,如图6所示。先从ESA*算法规划的全局节能路径中提取子目标点;然后让IDWA在相邻子目标点间进行局部路径轨迹规划,直至目标点。融合算法规划的路径对全局节能路径偏离较大,非最优节能路径,同时规划过程中机器人会因航向角调整问题常导致路径冗余、陷入局部解,寻路失败等问题,为此,本文将通过全局节能路径偏离评价和航向角自适应调整策略对融合算法进行改进。

图6 融合算法流程图

3.1 节能路径偏离评价

为避免额外能量损耗,设计全局节能路径偏离评价子函数Globdist(v,ω),使融合算法规划的路径更贴近全局节能路径。Globdist(v,ω)评价子函数结合全局节能路径信息,计算局部运动轨迹与全局路径的距离,其示意图如图7所示,计算公式为:

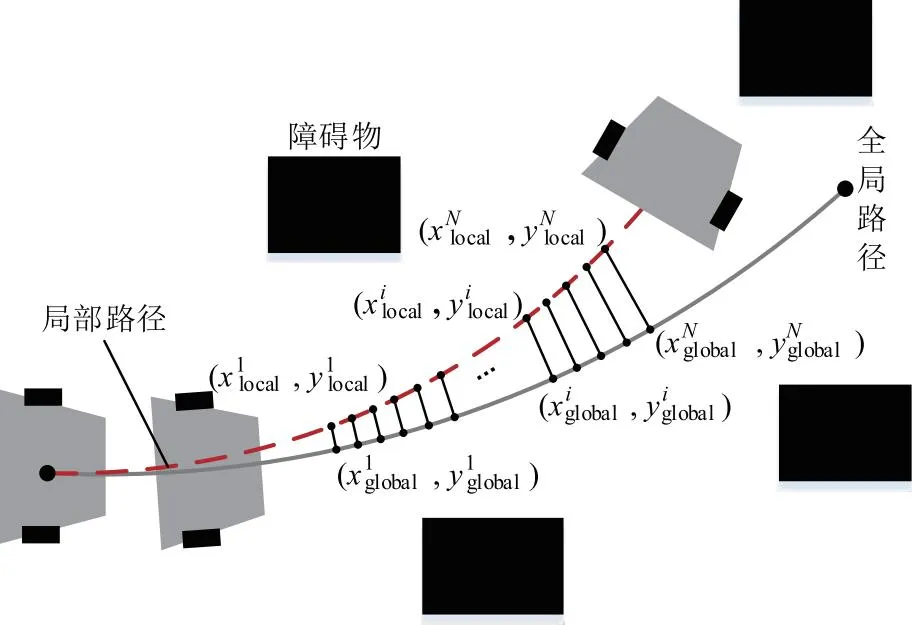
图7 节能路径偏离评价子函数示意图

Globdist(v,ω)=

(14)

融合算法优化后的评价函数为:

G(v,ω)=σ[αhead(v,ω)+βdist(v,ω)+γvel(v,ω)+

δEnergy(v,ω) +εGlobdist(v,ω)]。

(15)

其中ε为Globaldist(v,ω)评价子函数的加权系数。

3.2 基于全局节能路径的航向角自适应调整策略

在窄空间中,当机器人与动态障碍物相向而行时,如图8a所示,融合算法随机向左或向右选择方向,不考虑前方空间能否通过,容易导致机器人原地打圈调整航向角或与动态障碍物发生碰撞;当机器人与动态障碍物同向而行时,如图8b所示,融合算法可能会陷入局部解中,只能跟随动态障碍物缓慢前行,耗费大量时间;融合算法在相邻子目标点间进行局部路径轨迹规划时会因航向角产生累计误差,如图8c所示,导致路径冗余、陷入局部解。针对上述问题,本文对融合算法中航向角参数通过自调整策略优化。具体步骤如下:

图8 航向角调整情况示意图

步骤1计算子目标点hi-1、hi倾斜角度,计算公式为:

(16)

其中:arctan2()函数的值域为[-π,π];Δxi=xhi-xhi-1、Δyi=yhi-yhi-1为横、纵坐标的增量;φ为hi-1hi的倾斜角度;yawi-1i为hi-1hi段移动的理想航行角yawidea。

步骤2对hi-1hi进行动态障碍物检查,若有,则转步骤3执行航向角调整策略1;否则,转步骤4执行航向角调整策略2。

步骤3判断机器人与动态障碍物间左右区域内是否有静态障碍物,若有,则以yawidea为基准向右偏离yawout调整,更新状态参数(x,y,yawout,v,w);反之,则向左偏离yawout调整,转步骤6。yawout为航向角偏离阈值。

步骤4根据状态参数(x,y,yaw,v,w)获取机器人的实时航向角yawnow,将yawnow与yawidea进行比较,若yawin≤|yawnow-yawidea|,则转步骤5;反之,则不调整,转步骤6。其中yawin为航向角误差阈值。

步骤5若yawnow>yawidea,则对航向角参数进行动态减少,更新状态参数(x,y,yawnew,v,w),反之,则动态增大航行角参数。航向角参数动态调整的公式为:

yawnew=

(17)

其中:yawnew为动态调整的航向角,也为下一状态的起始航向角;κ为机器人转弯能力系数。

步骤6航向角调整结束。

4 实验与分析

4.1 实验环境地图

本文采用栅格法构建实验环境地图。为简化真实环境中的坡度、不规则障碍物在地图中的表达,作如下假设:

(1)在地图中忽略障碍物形状、高度等信息;

(2)非水平面上的区域以其投影地面的区域替代;

(3)机器人在非水平面上移动时的倾斜角与坡度角相等。

4.2 ESA*算法的路径优化方法对比与分析

4.2.1 平滑处理有效性验证与分析

为验证路径平滑方法的有效性,通过贝塞尔曲线平滑法[19](Bezier Curve Smoothing Method,BCSM)、过渡圆弧法[20](Transition Arc Method,TAM)以及本文动态弦定弧过渡法(String-Definite Arc transition Method,SDAM)进行对比验证,结果如图9所示,数据如表3所示。采用弯曲能量(Bending Energy,BE)和路径长度能量(The Bending Energy,TBE)[21]作为机器人路径平滑性的评价指标。

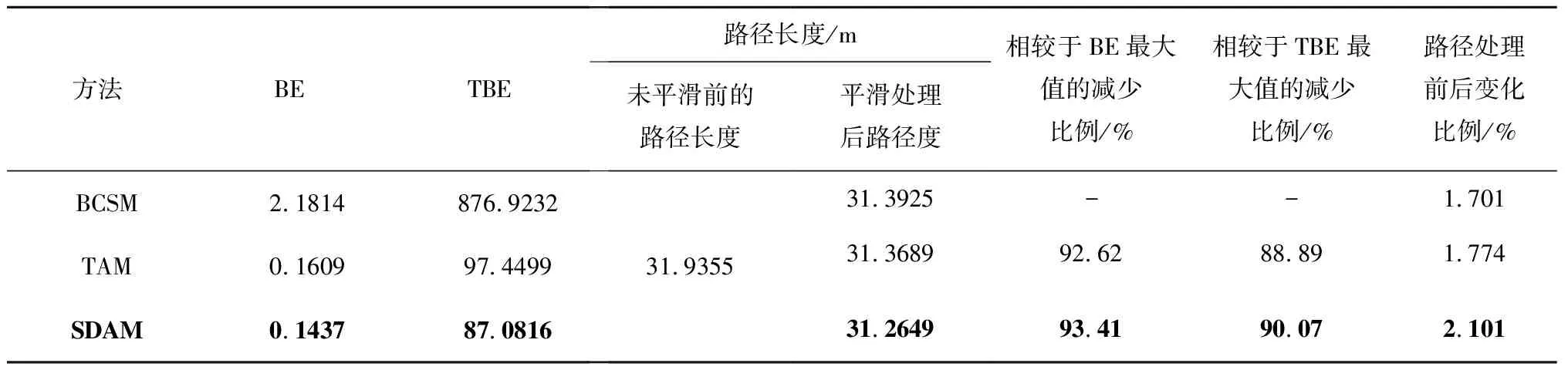
表3 路径平滑方法的实验结果对比

图9 路径转折点平滑处理结果

由图9a可知,同一环境下,BCSM、TAM和SDAM都完成了对转折尖峰的平滑处理,得到光滑连续的路径,但由表1和图10中可知,BCSM的路径曲率是最大的,TAM和SDAM的路径曲率相差不大但均远小于BCSM,其中BE和TBE值较BCSM分别减少了92.62%、93.41%,88.89%、90.07%;BCSM、TAM和SDAM处理后的路径长度较原路径均有减少,其中SDAM的减幅最大;由于BCSM平滑处理后的曲率和路径长度是最大的,从而导致TBE指标值较大。通过图9b的路径局部细节图可知,TAM方法平滑的路径会与障碍物发生碰撞,因为过渡圆弧半径的选取原则为转折点最短临边的比例定值,平滑处理过程不能动态改变圆弧半径,而BCSM和SDAM方法能保证优化路径的安全。综上分析,SDAM方法能设计出光滑连续、曲率合适、安全性高的路径。

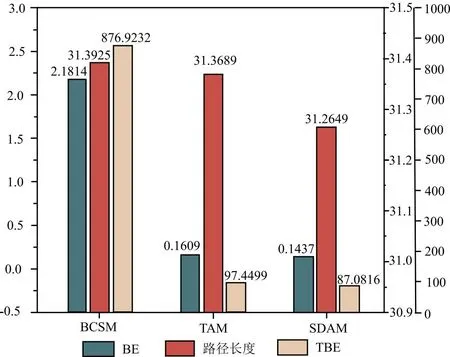
图10 路径平滑处理方法的性能指标对比

4.2.2 ESA*算法综合性能对比与分析

仿真环境如图11所示,其中栅格里的数字表示地面摩擦系数μ,绿色方框表示坡度为8°,红色的为12°。使用ACO算法、Dijkstra算法、传统A*算法、基于文献[8]、文献[10]、文献[22]和文献[23]的算法与ESA*算法进行机器人的全局路径规划,其规划轨迹如图12所示、性能指标结果如表4所示。为了能更直观地对比ESA*算法与其他方法在这些性能指标上的表现,对性能指标进行归一化以直方图形式进行表示,如图13所示。

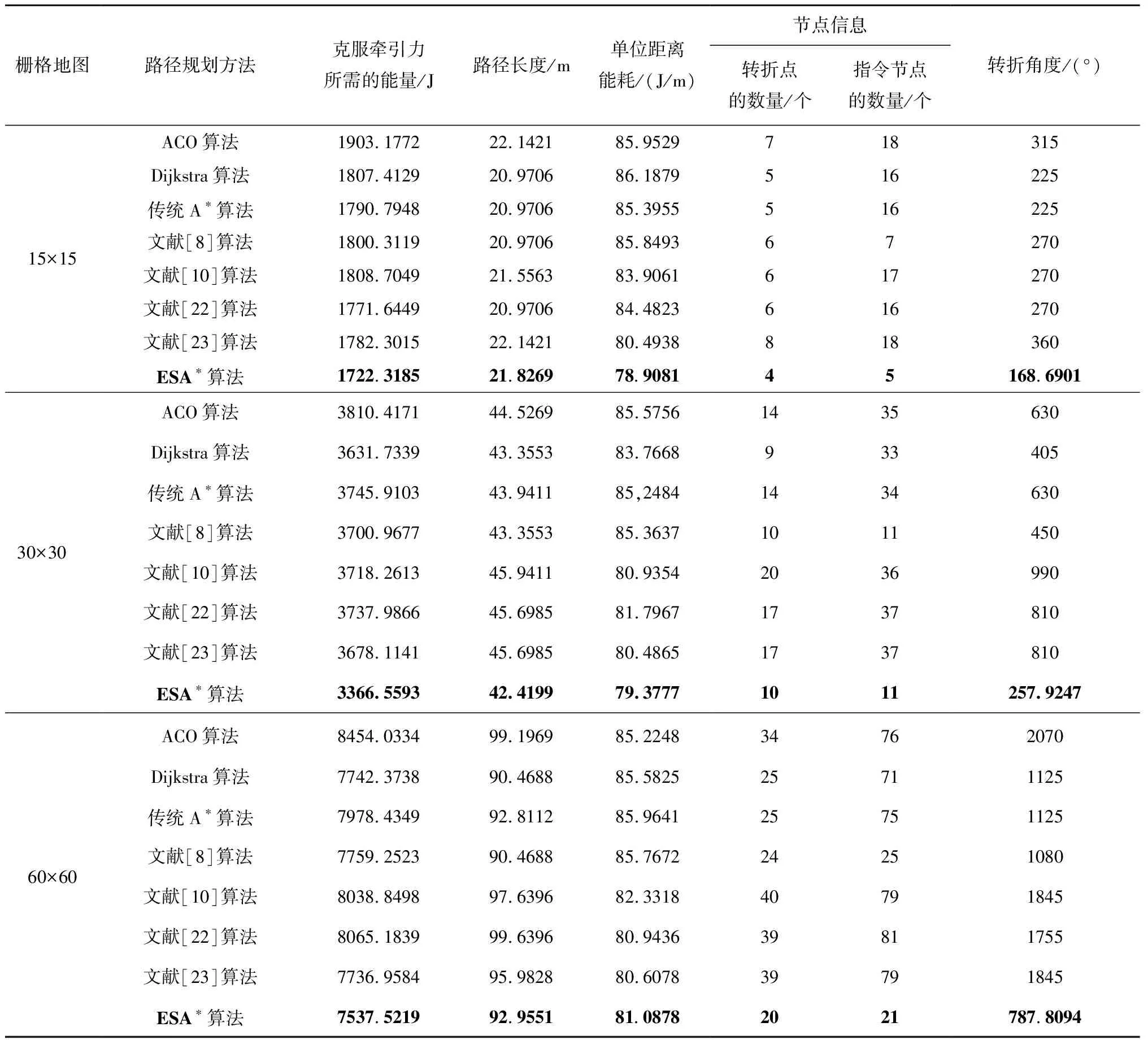
表4 移动机器人不同路径规划方法的实验结果对比

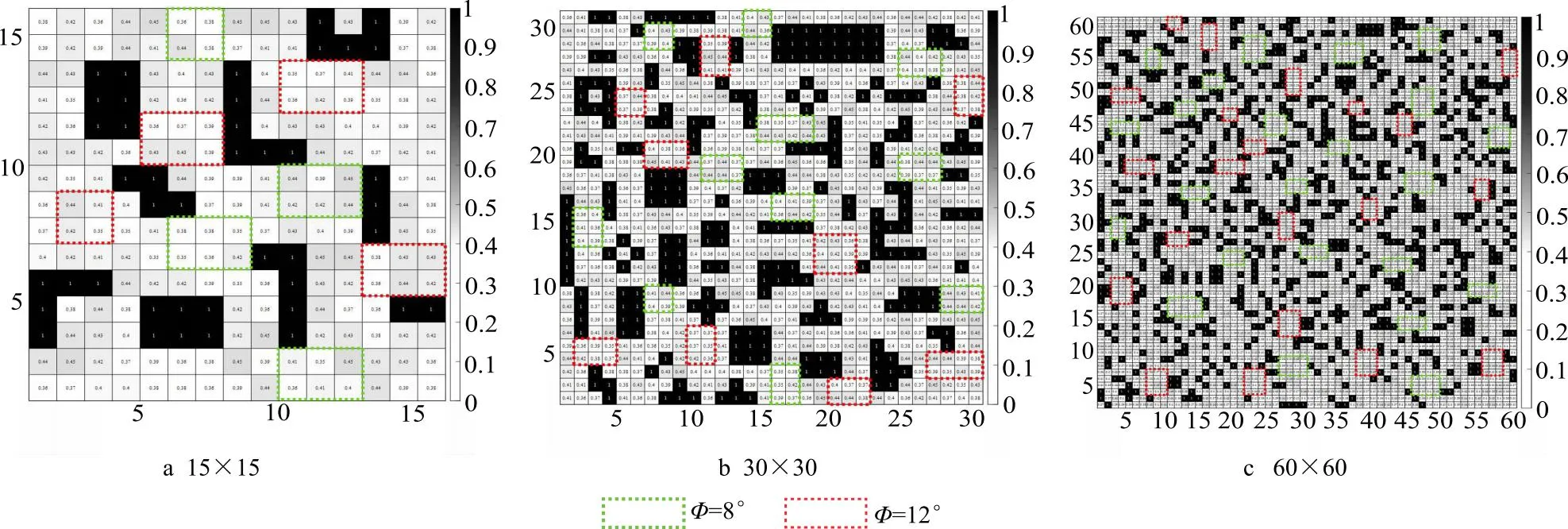
图11 实验仿真环境

图12 不同算法的路径规划轨迹

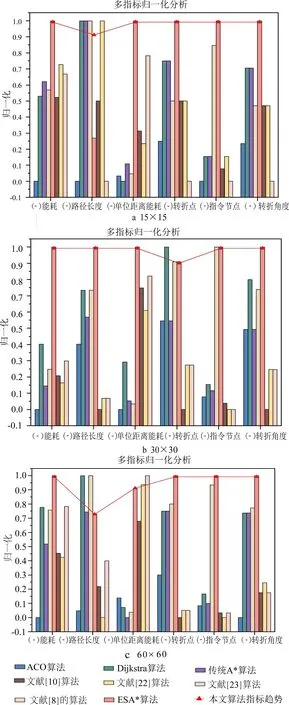
图13 多指标归一化分析

由图12的路径轨迹可知,上述算法在复杂度不同的环境下均能成功规划出路径,而由表4和图13中可知,ESA*算法的整体性能比其他算法要好。在能耗与路径长度方面,以路径长度为优化目标的ACO算法、Dijkstra算法、传统A*算法和文献[8]算法规划路径的长度与ESA*算法规划的路径长度相差不多,但在能量方面较ESA*算法耗费得多,在15×15、30×30与60×60环境中至少要多耗费68.609 8 J、265.174 7 J和204.851 9 J的能量,甚至于更多;与以能耗为优化目标的文献[10]、文献[22]和文献[23]算法相比,ESA*算法规划路径所耗费的能量最少,在15×15、30×30与60×60环境中至少减少了2.78%、8.47%和2.58%。相较于文献[22]没有考虑转弯能耗,ESA*算法不但在能耗上平均减少了316.138 6 J,而且路径转折数量也降低了43.55%,有效减少转弯带来的能量损耗。对于文献[23]中仅考虑爬坡能耗变化,ESA*算法全面考虑了坡度对机器人能耗的影响,能耗相比平均减少了190.324 8 J。ESA*算法较文献[10]相比,能量损耗和路径长度方面平均减少了6.93%和4.81%,从而有效提升了路径质量;从表4单位距离能耗数据可知,ESA*算法能为机器人规划出一条单位距离能耗较优路径,尤其是在规模不大的环境中。

在路径的平滑性上,ESA*算法较传统A*算法平均减少了22.72%的转向次数和70.41%的指令次数,同时路径累计转弯角度也平均减少了38.67%,明显提高了路径的平滑性;与文献[8]的路径平滑方法相比较,在转折点数量与指令节点数量相近的情况下,路径平均转折角度从600°减少到404.8°,有效减少了转弯的角度;而与ACO、Dijkstra等其他算法相比,ESA*算法无论在转折点数量、指令节点数量还是转折角度方面都有极大的提高。综合来看,ESA*算法在静态环境中能为机器人规划出一条低能耗且较为平滑的路径。

4.3 融合ESA*算法和IDWA算法的路径优化方法对比与分析

4.3.1 融合算法的仿真实验与分析

为验证改进融合算法的可行性,在空旷和密集两种复杂度不同的环境下分别用ESA*算法、IDWA算法、ESA*算法与传统DWA未改进的融合算法(传统融合算法)、ESA*算法与IDWA算法改进的融合算法(改进融合算法)作对比仿真实验,其结果如图14和图15所示。

图14 空旷环境下规划的路径轨迹

图15 密集环境下规划的路径轨迹

由图14a和图15a可知,在空旷与密集环境下,ESA*算法都能规划出连续平滑的全局路径,但由于ESA*算法本身不具备局部路径规划的特性,无法在动态环境中实时躲避随机的动—静态障碍物;在图14b和15b中可看出,IDWA算法在空旷的环境中能成功抵达目标点,但路径弯曲,不太平滑,当在密集复杂的环境中时,IDWA算法陷入了局部解,路径规划失败。由图14c、图14d和图15c、图15d分析可知,传统融合算法与改进融合算法在空旷环境下都能成功抵达目标点,但传统融合算法规划的路径对全局节能路径的偏离程度明显大于改进融合算法的,容易造成额外能量损耗;在密集环境下,改进融合算法能成功抵达目标点,而传统融合算法因航向角累计偏差陷入局部解,寻路失败。综合来看,相较于传统融合算法,改进融合算法更贴近全局节能路径,能有效减少额外能量的损耗,自适应调整航向角,避免产生冗余路径以及防止陷入局部解。

4.3.2 融合算法的避障实验与分析

为检验改进融合算法在窄空间中躲避动—静态障碍物的有效性和优越性,通过改进人工势法场(Improved Artificial Potential Field method,IAPF)[24]、改进Q学习算法(Improved Q-Learning Algorithm,IQLA)[25]以及基于A*和DWA优化的算法(The Improved A*and Dynamic Window Approach algorithm,TIA*-DWA)[26]与本文基于ESA*与IDWA的改进融合算法(the improved ESA*and IDWA algorithm,ESA*-IDWA)进行仿真对比实验,仿真结果如图16和图17所示,数据如表5所示。

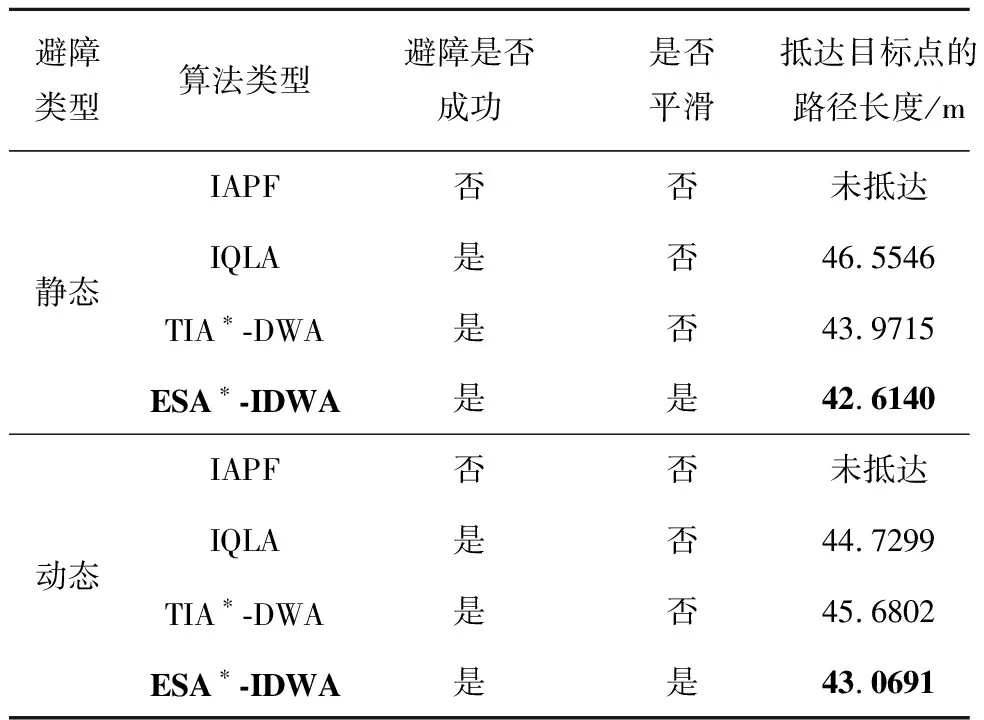
表5 仿真结果

图16 静态环境下的避障结果对比

图17 动态环境下的避障结果对比

在窄空间环境下,蓝色、黄色分别为静、动态障碍物。从图16a和图17a可知,IAPF算法避障路径规划失败,因为IAPF算法通过引入水流场改变斥力方向重新规划合力方向来调整前进方向解决路径振荡、陷入局部极小点、无法抵达目标点等问题,但在狭窄、单通道时面对长一字型、U型障碍物时斥力方向引起合力方向突变,导致路径振荡、陷入局部极小点。当在进行动态避障时机器人会从动态障碍物运动方向的前方运动,导致机器人与动态障碍物碰撞,避障失败。

从图16b、图16d和图17b、图17d中可知,IQLA、TIA*-DWA和ESA*-IDWA算法都成功避开动—静态障碍物,规划出从起始点到目标点的无碰撞路径,但从图16b、图17b和表5可知,IQLA的避障路径较长且存在转折点,路径不平滑,不利于机器人运动的平稳性。由图16c和图17c分析可知,机器人在窄空间中与动态障碍物同向而行且动态障碍物的速度小于移动机器人的速度时,TIA*-DWA算法会陷入局部解中,只能跟随动态障碍物缓慢移动,不能跳出;而当移动机器人与动态障碍物相向而行时,机器人不能正确调整自己的航向角,通过原地打圈调整航向角,造成冗余路径。根据图16d、图17d和表5可知,本文ESA*-IDWA算法的避障路径平滑且长度较短,较IQLA、TIA*-DWA的路径平均短6.14%、4.43%。在窄空间的动态环境中能有效躲避动态障碍物,自适应调整航向角,避免生成冗余路径,防止陷入局部解。总体来看,本文ESA*-IDWA算法能在窄空间的环境下完成动-静态障碍物的避障,且路径连续、平滑,更符合机器人的运动特性。

5 结束语

针对移动机器人因能量受限导致任务完成率低和在动态环境下避障灵活性差的问题,本文提出一种新的基于全局能耗最优路径下的局部能耗路径规划思路,并讨论了其可行性与有效性。本文主要贡献如下:

(1)考虑机器人运动过程中的耗能因素,建立能耗模型,提出基于能耗成本优化策略的ESA*算法并通过动态基准转折惩罚、三角剪枝与弦定弧过渡法相结合的路径优化方法解决因路径冗余、转折、转折角度大造成能量损耗的问题,得到全局能量损耗最优的平滑路径。

(2)将ESA*与IDWA算法相融合,并提出基于全局节能路径的航向角自调整策略优化传统动态窗口法,增强移动机器人避障能力,让其在动态、狭窄的环境下成功躲避动-静态障碍物。

(3)设计了全局节能路径偏离评价与能耗评价子函数改进融合算法,在基于全局能耗最优路径的基础上初步进行局部能耗最优路径规划的探索。

目前,全局能耗路径最优规划方法求解的能耗值是个预估值,机器人的真实能耗与局部运动规划息息相关。因此,后续的研究将围绕机器人局部能耗最优路径规划展开。