基于MARS的岩石抗拉强度预测模型
徐国权,王鑫瑀
(1.东华理工大学 地球科学学院, 南昌 330000; 2.河北钢铁集团矿业有限公司,河北 唐山 063000)
0 引 言
抗拉强度是反映岩石物理力学性质的基本参数之一,工程中岩石的拉伸破坏是其主要的破坏形式。对于许多岩体工程项目,在设计阶段以及后续岩体稳定性分析过程中都需要考虑的岩石的抗拉强度,因为抗拉强度是影响岩石破裂和失稳的关键指标之一[1]。Diederichs和Kaiser[2]指出抗拉强度是地下硐室临界稳定性的一个重要控制指标。
目前,对于岩石抗拉强度测试,国内制定的岩石力学试验标准[3-4]和国际岩石力学学会(International Society for Rock Mechanics,ISRM)[5]及美国材料与试验协会(American Society for Testing and Materials,ASTM)均推荐采用直接拉伸试验或间接测量法(如:巴西劈裂试验、弯曲试验法等)[6-9]。从理论上来说,直接拉伸试验的测试结果与岩石的抗拉强度最为接近,然而该方法在拉伸试验过程中往往受到仪器设备、岩石试样制备困难等因素的影响,导致试验过程中许多测试结果是无效的,因此很少被采用。巴西劈裂试验由于其试验设备操作简便对试样要求相对较低,已经成为最常用的间接测量方法,尽管使用这种方法也会得到一些无效结果[10]。为了得到可靠的测量数据,通常需要制备高质量的岩石试样,这往往需要花费大量的时间和费用。
虽然通过试验方法来获得岩石抗拉强度一直是工程设计的首选,但是在项目的初期阶段,研究人员更倾向于建立经验模型[11-13]或采用统计方法来间接估算岩石的抗压强度[14-15],以节约成本。近年来,采用无损检测技术并结合机器学习方法来预测岩体的力学性质已经成为热门研究方向之一。通过一些与岩石物理力学性质相关且易于测量的参数,建立智能预测模型,可以经济、快速和准确地获取一些重要的岩石物理力学参数。Behnia等[16]采用基因表达式编程(Gene Expression Programming, GEP)建立预测模型,通过测量岩石的石英含量、干密度和孔隙度,对完整岩石的抗压强度和静弹性模量进行预测,并取得了令人满意的结果。Hasanipanah等[17]尝试使用元启发算法来预测岩石抗拉强度,萤火虫优化算法(Fire-fly Algorithm,FA)被用来训练和优化自适应神经模糊推理系统(Adaptive-Network-based Fuzzy Inference System,ANFIS)的超参数。结果表明经过优化后的FA-ANFIS模型能够稳定有效预测岩石抗拉强度。
Parsajoo等[18]分别使用模糊推理系统(Fuzzy Inference System,FIS), ANFIS和人工神经网络(Artificial Neural Networks,ANN)三种智能算法对岩石抗拉强度进行预测。他们选择斯密特锤回弹数、P波速度和密度作为输入参数,巴西抗拉强度作为输出参数。共有超过150块花岗岩试件被收集到实验室进行测试,最终得到包含127组数据的数据集。结果表明ANFIS算法能够结合FIS和ANN算法的优点,是一种功能强大且适用的模型。Huang等[19]建立了一种基于ANN的岩石抗拉强度预测模型,他们采用施密特锤试验、干密度试验和点荷载结果作为输入参数,岩石抗拉强度作为输出参数建立预测模型,为了提高ANN模型的预测性能,分别使用入侵杂草优化算法、帝国主义竞争算法和人工蜂群算法对ANN模型进行了优化。结果表明,经过优化后的ANN模型是一种可靠的工程解决方案。Canakci和Pala[20]构建了一个ANN模型,利用声波速度、干密度、施密特回弹数和吸水率来估计岩石的抗拉强度。此外,他们还提出了基于上述参数来计算玄武岩抗拉强度的经验公式。Yilmaz和Yuksek[21]分别使用多元回归分析和ANN对岩石抗压强度和杨氏模量进行预测。他们指出抗压强度和杨氏模量与耐久性指数、点荷载指数、有效孔隙度和施密特回弹数之间存在统计学意义上的关系。尽管ANN模型在岩石物理力学性质预测方面表现出很好的效果,然而ANN属于“黑箱”模型,可解释性较差。
多元自适应回归样条(Multivariate Adaptive Regression Splines,MARS)是一种新颖的用于描述非线性关系的数据建模技术。它具有以下优点:
(1)数据驱动建模。
(2)MARS能够在没有很强的模型假设的情况下,对变量之间的复杂非线性关系进行建模。
(3)当存在较多潜在的自变量时,MARS可以获得自变量对因变量的相对重要性。
(4)MARS不需要长时间的训练过程,因此可以节省大量的模型构建时间,特别是在数据量比较大的情况下。
(5)与ANN等“黑箱”技术相比,MARS的突出优势是模型的可解释性,它能够识别出建模过程中变量的重要性。
本文基于MARS算法建立岩石抗拉强度预测模型,使用某引水隧道数据库[21],考虑了斯密特锤回弹数、干密度、点荷载强度指标和巴西抗拉强度等参数。除了MARS模型外,还建立了传统的决策树(Decision Tree,DT)、ANN和支持向量机(Support Vector Machines, SVM)模型用于岩石抗拉强度预测,并对上述4种机器学习模型进行性能进行了比较。
1 多元自适应回归样条
MARS是一种非参数回归方法[22-23],它不需要对输入变量和输出变量之间的潜在函数关系做出假设。MARS以非线性的形式建立自变量和因变量之间的关系,并识别自变量之间的相互作用和条件关系。MARS将数据以等效间隔划分若干分区,并对每个分区进行回归,得到一系列不同梯度分段曲线(样条),以此来模拟输入和输出之间的非线性响应。分段曲线的端点称为节,它标志着一个分区的结束和另一个分区的开始。最终得到的分段曲线通常用基函数(Basis Functions,BFs)来表示,这使得MARS模型具有很高的灵活性。其中,分段线性BFs可以表示为:
(1)
(2)
式中:τ表示节点;x为横坐标取值。这里每个函数都是分段线性的,并在值τ处有一个节。一个基本的BFs如图1所示。

图1 MARS中的BFsFig.1 Basis functions in MARS
模型输入变量和输入变量之间的关系可表示为
Y=f(X)+ε。
(3)
式中:Y为输出变量;X=(X1,X2,X3, …,Xn)T为预测因子的向量;ε为可加的随机变量,假设为0。MARS通过BFs逼近函数f,可以将f(X)表示为一个线性组合,该组合由BFs和截距构成,表示为
(4)
式中:M为BFs的数量;λm为BFs,它可以是一个样条函数,或者是模型中已经包含的两个或多个样条函数的乘积。系数βi(i=0,1,2,…,M)是常数,可以通过最小二乘法计算得到。
MARS模型建立过程一般分为两个阶段,首先是前向选择阶段,逐步生成MARS模型的候选BFs。在这一阶段,BFs被搜索并添加到模型当中,当达到最大允许BFs数量时,程序停止。此时,MARS创建了一条弯曲的回归线来拟合每个分区,但这通常会导致模型过拟合。
接下来进入向后剪枝阶段,从MARS模型中修剪BFs,逐步从模型中删除那些贡献较小的BFs。在这一阶段,如果一个自变量的BFs对提高MARS模型预测性能没有任何意义,可以将它从模型中完全删除。
最后,MARS模型使用广义交叉验证(Generalized Cross Validation,GCV)作为最终模型选择标准。GCV可以表示为
(5)

C(B)=(B+1)+dB。
(6)
式中:d为每个BFs优化的惩罚因子;B为BFs的数量。
MARS最小化GCV,降低了模型估计的偏差,但同时由于引入了额外的参数,增加了方差,以提高模型的拟合。
2 数据收集和准备
本文的目的是使用数据驱动建模技术来预测岩石的抗拉强度。数据来源于某引水隧道施工过程中所收集到的100组花岗岩样品[22-23]。这些样品在加工完成之后,被转移到实验室进行岩石力学测试,其中测试内容包括变量斯密特锤回弹数、干密度、点荷载强度指标和巴西抗拉强度,上述参数的测量均按照ISRM标准执行,最终得到80组数据,表1中给出了测量结果概况。

表1 数据概况Table 1 Summary of the dataset
相关性矩阵给出了输入变量斯密特锤回弹数、干密度、点荷载强度指标与输出变量巴西抗拉强度之间的相关性,如图2所示。输入变量的皮尔逊相关系数R均>0.8,表明输入变量同输出变量的相关性较高。

图2 相关性矩阵Fig.2 Correlation matrix
整个数据集被随机划分为两部分,其中70%的数据(56组数据)作为训练集,用于建立模型,剩余30%的数据(24组数据)作为测试集,用于评估模型性能。
在建模之前,需要对数据进行标准化处理。使用最大最小归一化的方式将数据归一化到0和1之间,其方程为
(7)
式中:x为原始数据;xmax和xmin分别为数据集中的最大值和最小值;xnorm为x的归一化值。
3 建立模型
基于MatLab软件建立MARS模型对岩石抗拉强度进行了预测,为了更好地评估MARS模型的性能,使用相同的训练数据和测试数据开发了DT、ANN、SVM模型,并将其同MARS模型的预测结果进行比较。
机器学习模型的性能在很大程度取决于模型的超参数设置,通过调整超参数可以提高模型的性能。为了确定每个模型的最佳超参数组合,通常可以采用交叉验证的方式。在交叉验证中,数据集被随机分成k个大小相等的子集。在k个子集中,保留一个子集作为模型测试的验证数据,其余k-1个子集作为训练数据。这一过程重复k次,这样每个子集都作为一次验证集,常用的10折交叉验证如图3所示。模型的误差可以通过k次试验的平均验证误差来表示。

图3 10折交叉验证Fig.3 Ten-fold cross validation
这里使用10折交叉验证得到4种机器学习模型的超参数组合如表2所示。

表2 模型超参数Table 2 Hyper-parameters in developed models
4 评价指标
为了评估所开发模型的性能,选取了4种常用的模型性能评价指标。它们分别为均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)、相关系数(Correlation Coefficient,CC)和决定系数(R2),其表达式分别为:
(8)
(9)
(10)
(11)

理论上,RMSE和MAE越接近于0说明模型的性能越好,RMSE反映出测量数据和预测数据之间的偏差,而MAE则可以准确反映实际预测误差的大小。CC和R2则是越接近于1表明模型拟合越好。
5 结果和讨论
5.1 MARS预测结果分析
根据选定的模型超参数,MARS在前向逐步阶段选取了50个BFs建立MARS模型。接下来,后向剪枝阶段删除多余的基函数。最终得到的模型包括13个BFs,其对应公式如表3所示。最终得到的MARS模型的巴西抗拉强度BTS为

表3 基函数及其方程Table 3 BFs and their corresponding equations
(12)
MARS模型的训练和测试性能由式(12)决定。式(12)和表3可以解释收敛如何随输入变量的变化而变化。表3中一些BFs的系数是负值,如BF1、BF3、BF6、BF7、BF9、BF10、BF11。在不深入详细分析每个方程的情况下,这些负系数可能表明当Rn、DD和Is50增加时收敛性降低。
方差分析(Analysis of Variance,ANOVA)是一种被广泛使用的统计方法,通常用于识别高维模型中的重要变量和变量之间的交互作用。利用训练数据对模型进行ANOVA分解,其结果如表4所示。表中的每一行总结了每个ANOVA函数的ANOVA分解,而每一列则是每个分解的汇数量,其中第1列为函数编号;第2列给出了函数的标准差,这个标准差表明了它对整个模型的(相对)重要程度,可以类比于线性模型中的标准回归系数;第3列提供了反映方差函数相对重要性的另一个指标GCV评分,它可以用来判断这个方差分析函数是否对模型做出重要贡献,或者仅仅是略微有助于提高整体GCV评分;第4列给出了构成ANOVA函数的BFs数量;最后第5列表明了与ANOVA函数相关的自变量。从表4中可以看到,ANOVA函数3做出了最大的贡献,它主要与Is50有关,同时函数1、2和4对模型的贡献相对较小,它们分别与变量Rn和变量DD有关。

表4 方差分析结果Table 4 ANOVA decomposition
5.2 性能比较
表5给出了4种模型在训练和测试阶段的性能指标计算结果,所开发的4种模型均表现出良好的预测效果,相关系数均>0.9,R2均>0.8。此外,所有的模型RMSE均>0.1,且均<0.9。综合性能评估结果,与DT、ANN、SVM模型相比,在训练和测试阶段,MARS模型均表现出最高的精度。SVM模型次之,DT和ANN模型表现相对较差,但在训练阶段DT和ANN模型表现要好于SVM模型。
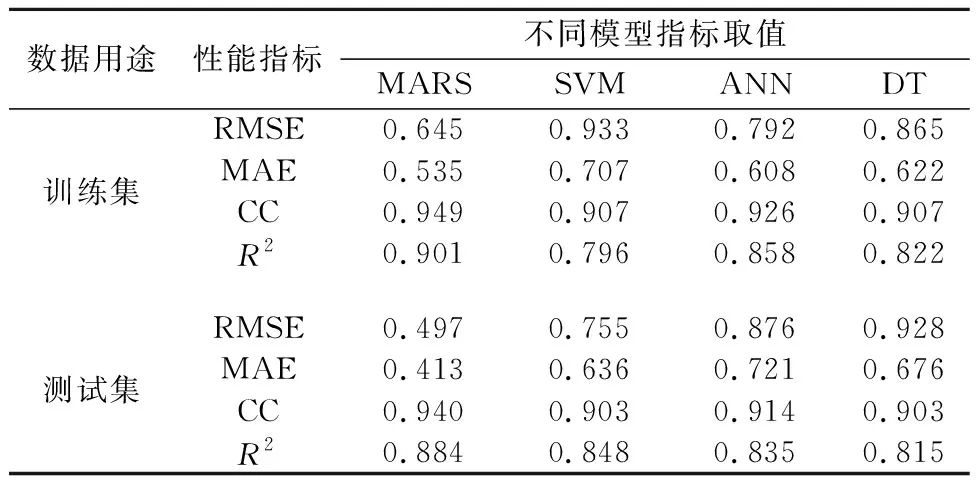
表5 模型在训练和测试阶段的性能指标Table 5 Performance indexes of developed models in training and testing stages
图4给出模型预测值与真实值之间的差异,可以看到,MARS模型的预测值最接近实测值,模型在训练和测试阶段的R2分别为0.901和0.884,均高于其他模型。SVM模型的R2在训练阶段低于ANN和DT模型,然而在测试阶段却高于ANN和DT模型,且同MARS模型之间的差距达到0.036。

图4 训练和测试阶段测量值和预测值的关系Fig.4 Actual values versus predicted values in training and testing stages
本文引入泰勒图[24]以图形化的形式来比较4种模型的预测性能,如图5所示。标准的泰勒图可以通过均方根误差、相关系数和标准差来量化实测值和预测值之间的关系。泰勒图的结果再次证明MARS模型的预测精度高于其他3种模型。

图5 训练和测试阶段的泰勒图Fig.5 Taylor diagrams in training and testing stages
6 结 论
数据驱动建模技术被认为是解决复杂工程问题的有效工具,本文研究了MARS模型在估计岩石抗拉强度方面的潜力。开发了MARS、DT、ANN和SVM4种预测模型。主要结论如下:
(1) 综合比较了4种模型的预测结果,所开发的4种机器学习模型都表现出了良好的性能。其中,MARS模型的整体性能最高(均方根误差和平均绝对误差最低,相关系数和R2最高),其次是SVM和ANN模型,DT模型的整体性能最低。
(2) MARS在寻找最优模型方面的计算效率更高,并且可以通过ANOVA分解提供每个变量对岩体抗拉强度估计的贡献,使得模型具有更好的可解释性。在本研究所选择的3个输入参数中,点荷载强度的贡献较大,斯密特锤回弹数和密度贡献相对较小。
(3) 本文给出了MARS模型的方程,在有适量现场数据的情况下,这些模型方程可以被用于预测岩石抗拉强度。研究结果表明,数据驱动建模技术在岩石抗拉强度预测方面有着很大的前景。
(4)岩石抗拉强度预测面临的挑战是,来自不同地区、不同类型的岩石往往表现出不同的性质,这可能会限制预测模型的鲁棒性。为了丰富数据库,进一步提高MARS模型的通用性和应用范围,还需要尽可能多的收集不同地区、不同类型岩石抗拉强度数据。

