库水作用下滑坡土体渗流与蠕变耦合试验研究

王 力,孙文铎,王世梅,胡秋芬,陈玙珊,南芳芸

(1.三峡大学 三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002; 2.三峡大学 土木与建筑学院,湖北 宜昌 443002; 3.中国地质大学(武汉) 湖北巴东地质灾害国家野外科学观测研究站, 武汉 430074); 4.河海大学 岩土力学与堤坝工程教育部重点实验室,南京 210024)

0 引 言

大量实例表明,水库蓄水后,库水长期反复大幅度涨落加剧了库岸滑坡灾害的发生,但滑坡变形演化失稳并不是立即发生的,大都经历了一个时间发展过程[1-3]。如美国Grand Coulee水库自1941年开始蓄水后发生滑坡500起,近49%的滑坡发生在开始蓄水后2 a内,其余均发生在2～12 a之间[4];我国三峡水库自2003年开始蓄水以来诱发变形的滑坡有151起,累积最大位移>1 000 mm的大型滑坡达14个,绝大多数滑坡变形随时间在不断增加。如三峡库区树坪滑坡累积位移已达4 000 mm有余[5],分析图1中库水位与地表位移监测曲线知,库水位周期性的升降,地表位移变形速率也随之增大和减小,且地表累计位移曲线的变化趋势为连续形阶梯上升。即使在库水位稳定时期,此刻对应的地表位移仍保持继续增大的趋势。这就表明了在滑坡变形过程中,地表位移不仅会受到库水位升降引起的渗流场变化影响,也会受到滑坡土体本身存在的蠕变效应的影响。库水位变动诱发滑坡变形或失稳具有显著的时间效应,其力学过程十分复杂,既包括地下水渗流产生的时间效应,也包括蠕变产生的时间效应,两种时间效应相互叠加交织在一起。

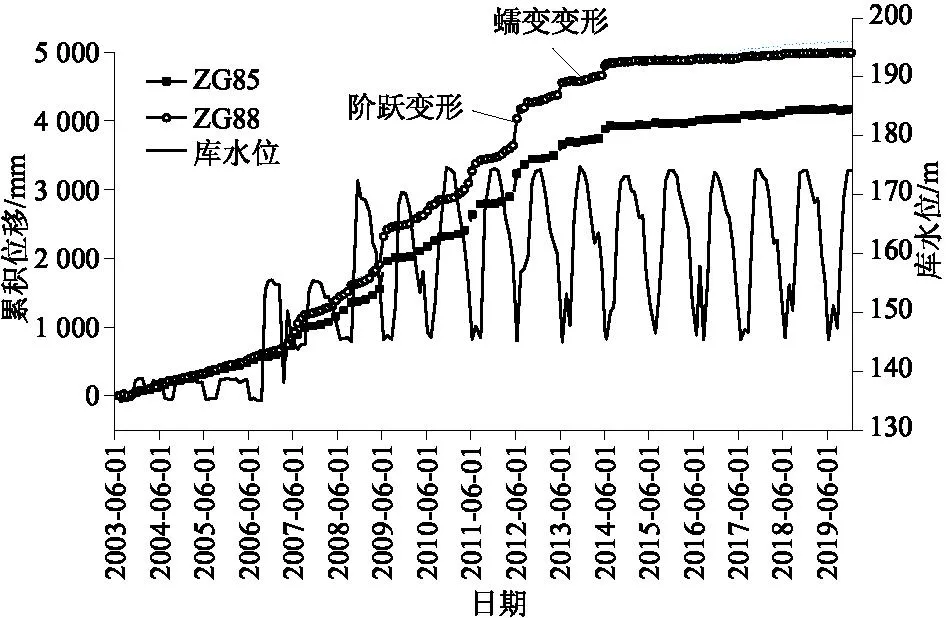
图1 树坪滑坡库水位及变形监测曲线Fig.1 Monitoring curves of reservoir water level and deformation of Shuping landslide

针对上述不足,本研究拟以三峡库区典型滑坡为研究对象,利用自主研发的渗流与蠕变耦合试验仪及改进后的GDS三轴仪,对渗流与蠕变相互影响展开系列试验研究,揭示土样渗流与蠕变耦合作用的物理特性,建立反映土体流固耦合效应的耦合桥梁,为后续构建渗流与蠕变耦合数学模型提供相关参数。

1 渗流对蠕变影响的试验研究

本文在针对渗流与蠕变耦合力学过程的研究中,通过开展定水头渗流试验来探究渗流对变形的影响作用,并进一步揭示其影响规律与作用机理,对渗流与蠕变耦合过程的规律分析及机理研究具有一定参考意义。

1.1 试验仪器和方法

试验仪器采用自主研发并由南京土壤仪器厂生产的SRS-1型三联渗流与蠕变耦合三轴试验仪。该试验仪器(图2)将三轴蠕变仪的加载及测量系统和非饱和渗透试验仪的渗流供水系统及渗流量测量系统有机结合在同一个试验系统中。其优点在于既能测得试验过程中土样的体积变化又可测量渗透系数,该渗流与蠕变耦合三轴试验仪可用于测定在一定的周围压力、主应力、渗透水压力作用下的渗流与蠕变特性,进行渗流与蠕变相互作用下的变形机理研究。仪器由压力控制系统(包括围压控制系统、轴压加载系统、渗透水压控制系统)、三轴压力室、量测系统(包括孔压、体积应变、轴向应变和渗流量量测系统)及数据采集系统等几部分组成(结构示意图见图2)。

图2 三联渗流与蠕变耦合三轴试验仪Fig.2 Seepage and creep coupling triaxial test instrument

试验方法及操作步骤如下:

(1)制样。试样采用单向分层击实法。土样风干碾散,过2 mm筛,配成含水率15%的湿土状,分为5层击实,保持每层土样质量相等,且每层接触面刨毛。再将土样装入饱和器内,采用真空饱和方法饱和土样。

(2)装样。装样时,需要先将仪器各连接管道内的空气排出,再将提前制备的土柱试样套在橡胶膜中放置并绑扎在压力腔内部的底座上,最后通过注水口往压力室内注满无气水。同时在试验初期,施加20 kPa的围压对试样进行预压,使橡胶膜完全贴合于试样之上。

(3)排水固结。逐级施加围压进行排水固结。固结排水稳定标准规定为:2 h固结排水量<0.1 mL。

胼胝体的嘴和膝部分别接受来自前交通动脉的胼胝体下动脉和胼胝体内侧动脉的血液供应。胼周动脉是大脑前动脉(anterior cerebral artery, ACA)的延续，共发出4条分支是胼胝体体部的最主要供血动脉。胼周后动脉是一条小的穿支动脉，来自于大脑后动脉(posterior cerebral artery, PCA)供应胼胝体的压部。研究发现胼胝体后方近压部处有ACA和PCA吻合支。胼胝体同时接受前循环和后循环供血，因此单纯的ACA或PCA阻塞并不会完全阻断胼胝体的血液供应，而导致严重的胼胝体梗死[3, 5]。

(4)渗流。待试样固结稳定后,施加渗透水压,观察渗流过程中土样的体积变形规律。

考虑到渗透水压施加初期,试样变形较快,随后变形逐渐趋缓,为充分反映这种变形特点,数据采集采取先小后逐渐增大的策略。

1.2 试验土样及方案

试验所用土样取自三峡库区秭归县莲花沱2号滑坡滑体,为位于消落带位置的粉质黏土,滑坡工程地质剖面图与取样位置见图3。试验采用重塑样,参考《公路土工试验规程》(JTG 3430—2020),对土样进行了基本物理力学性质试验,结果见表1。

表1 某滑坡土体常规物理力学性质指标Table 1 Conventional physical and mechanical properties of soil mass of a landslide

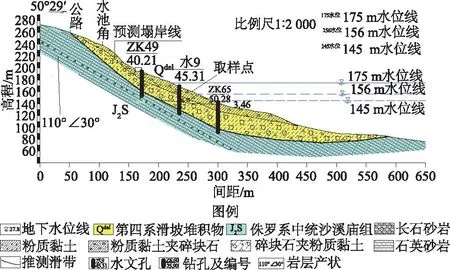
图3 莲花沱2号Ⅰ-Ⅰ′滑坡工程地质剖面图Fig.3 Engineering geological profile of Lianhuatuo No.2Ⅰ-Ⅰ′ landslide

针对渗透作用对土样变形的影响规律的试验方案设计如下:对试样逐级施加围压至150 kPa,并在固结稳定后再施加100 kPa的渗透水压。渗流对变形影响的稳定标准规定为:试验过程中观测土样的体积变形量趋于稳定。

1.3 试验结果

土样的体积应变和孔隙比e随时间t的变化结果如图4所示。可以看到在100 kPa渗透压作用下,土样的体积变形和孔隙比随时间的变化规律较一致且具有同步性。土样的体积变形可以分为快速膨胀回弹、稳定和缓慢压密3个阶段:

(1)膨胀回弹阶段。在对土样施加渗透压初期,土体内部孔隙水压力会在短时间内快速增大,这不仅会使其产生超孔隙水压力,同时孔隙比也随之增大,并在1 500 min达到峰值。此阶段超孔隙水压力对试样的作用会使有效围压下降,即产生围压卸荷的作用,从而发生体积回弹变形。

(2)稳定阶段。体积应变达到峰值后的1 500～2 000 min为土样的短期稳定阶段,此时随着土体内部积累的超孔隙水压力消散,渗流力作用与土样内部有效应力下降造成的回弹变形效应处于平衡状态,因此该阶段土样的变形未出现较大变化。

(3)压密阶段。稳定阶段后随着耦合作用的进行,土样内部的有效应力减小至一定值后趋于稳定,与之相关联的回弹变形也随之稳定;但渗流力依然对土体渗流场产生影响,因而在此阶段土样体积应变在渗流作用下缓慢压缩减小。

由此可知,围压和渗流力均会对土体积应变形产生影响,为了研究其各自作用过程的力学特性,还需分开探讨渗流作用中渗流力和有效应力变化对土体的变形影响作用。

2 变形对渗流影响的试验研究

2.1 试验方案

试验土样与试验仪器同前。 本试验为研究不同应力作用下土样的变形对渗透系数的影响, 试验设计的总体思路为: 首先施加不同的围压对土样进行排水固结, 待固结稳定即试样变形稳定后, 再施加对应的渗透水压进行渗流, 就可以测得土样变形稳定后的渗透系数。 具体试验方案详见表2。 制样、装样步骤同前, 由于多个试验土样在制作过程中会出现差异性, 为避免对试验结果造成影响, 本试验选择在同一个土样上施加围压条件。 即逐级对土样施加固结围压时, 待一级围压下固结稳定后, 施加对应的渗透水压, 至渗流稳定后测得此时土体的渗透系数, 并在此基础上继续进行下一级的固结渗透试验。

表2 粉质黏土试验方案Table 2 Experiment scheme for silty clay

2.2 试验结果

按照表2的试验方案,得到围压分别为50、100、150、200、250 kPa和对应的渗透压分别为40、90、140、190、240 kPa时土样孔隙比随时间的变化规律,如图5所示。可以看出,开始时,土样孔隙比随时间的增长而逐渐增大,施加渗透压初期孔隙比变化较快,但变化速率随时间逐渐减小,最后趋于平缓稳定状态。主要原因是土样排水固结稳定后对土样进行渗流,渗流时土样中孔隙水压力增大,根据太沙基有效应力原理可知,所施加围压一定即总应力不变,而孔隙水压力增大,此时土颗粒间的有效应力将变小,土骨架将产生一定量的回弹,这将导致土样孔隙比变大。

图5 孔隙比随时间的变化曲线Fig.5 Variation of void ratio with time

试验得到土样孔隙比和渗透系数的关系见表3,关系曲线见图6。传统做法获取e-k(孔隙比-渗透系数)关系时未考虑渗流导致的孔隙变形,对于同样的渗透系数,传统做法对应的孔隙比与本研究相比较小。因此,没有考虑渗流对变形影响的传统做法并不能反映岩土体渗流时的真实流固耦合现象。

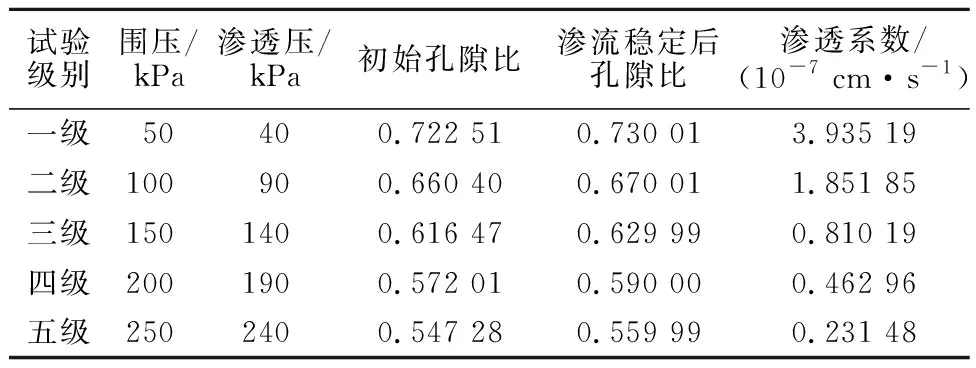
表3 土样孔隙比和渗透系数的关系Table 3 Relationship between void ratio and permeability coefficient of soil samples

图6 土样的e-k关系曲线Fig.6 Relationship curves of e-k of soil samples

3 渗流与蠕变耦合试验

3.1 试验仪器及改进

考虑到上述试验设备无法获取精确以及连续的试验结果,难以真实反映水库滑坡土体的流固耦合效应。本项研究将对GDS三轴仪进行改进设计,以完成高精度控制和量测的渗流与蠕变耦合试验,从而可以更为科学严谨地进行渗流与蠕变耦合作用的力学特性研究及分析。

改进设计的总体思路为:基于自主研发的非饱和渗透试验仪[20]的基本原理,将GDS三轴仪设计成既能测得试验过程中土样的体积变化,又可测量渗透系数的渗流与蠕变耦合三轴试验仪,可用于测定在一定的周围压力、渗透水压力作用下的渗流与蠕变特性。改造后的渗流与蠕变耦合三轴试验仪(图7)主要由渗透水压控制器、围压控制器、三轴压力室、孔压和体积应变量测系统、渗流量量测系统、数据采集系统等部分组成。

图7 渗流与蠕变耦合三轴试验仪实物照片Fig.7 Photo of seepage and creep coupling triaxial test instrument

渗透水压控制器在轴压控制器的基础上改装而成,通过塑料软管与试样上帽连接,用来测量与设置试样所需要的渗透水压目标值。渗透水压控制器压力量测的精度为0.1 kPa。渗透水压控制器内的水体积变化量即为渗流进水量,其精度为1 mm3。渗流量量测系统则是在反压控制器的基础上改装而成,通过塑料软管连接试样底座,当试验开始时试样中的水会通过底座与量测系统做交换,因而可以通过量测到的水体积变化量来获取渗流量,其精度为1 mm3。为了实现该改装方案,专门设计制作了配套的底座和试样帽,如图8所示。

图8 设计制作的底座和试样帽部件Fig.8 Photos of designed and manufactured base and sample cap

3.2 试验方案及方法

试验土样同前,试验的总体设计方案如下:逐级施加围压至100 kPa下固结完成,再施加90 kPa渗透水压,直至试样变形和渗透系数变化稳定。制样、装样与排水固结步骤同前,渗流与蠕变耦合的方法如下:待试样固结稳定后,施加90 kPa的渗透水压进行渗流与蠕变耦合试验,观测土样的体积变形和渗透系数的变化,直至土样的体积应变和渗透系数稳定不变,即为渗流与蠕变耦合试验结束。

3.3 试验结果

进行90 kPa渗透压作用下的渗流与蠕变耦合试验,总历时25 d,渗流与蠕变耦合阶段历时14 d。得到土样体积应变、孔隙比e、渗透系数k随时间t的变化规律,详见图9,同时得出渗流与蠕变耦合过程中土样孔隙比e和渗透系数k的关系曲线见图10。

图9 耦合作用下土样体积应变、孔隙比、渗透系数随时间的变化曲线Fig.9 Time-dependent variations of volume strain, void ratio, and permeability coefficient of soil samples under coupling action

图10 耦合作用下土样孔隙比e与渗透系数k的关系曲线Fig.10 Relationship curves of void ratio e and permea-bility coefficient k of soil samples under coupling action

由图9和图10可以看出土样的体积应变、孔隙比及渗透系数随时间的变化规律较一致,土样的孔隙比与体积应变的变化规律完全吻合。主要经历了3个阶段:施加渗透压耦合初期的快速增大阶段;变形或变化达到顶峰暂趋稳定后的缓慢减小阶段;变形或变化缓慢趋于稳定阶段。

图9(a)表明,土样在流变耦合作用下,其体积应变趋势经历了先快速增加到峰值,短期稳定后再到缓慢减小的过程。根据太沙基有效应力原理,施加在土样上的围压一定,等同于总应力值不发生变化,前期的体积变化是由于渗流导致土样内孔隙水压力迅速增大,进而使土粒间有效应力降低,土体在宏观上发生回弹变形,因此处于此阶段土样的体积迅速增大,并在2 560 min出现第一个小峰值;而在体积应变达到峰值后,会进入短期稳定阶段,此时渗流力作用与土样内部有效应力下降造成的回弹变形效应处于平衡状态,因此该阶段土样的变形未出现较大变化。随着耦合作用的进行,土样内部的有效应力减小至一定值后趋于稳定,与之相关联的回弹变形也随之稳定;但渗流力依然对土体渗流场产生影响,因而在此阶段土样体积应变在渗流作用下缓慢减小。总体而言,在土样的渗流与蠕变耦合试验中,影响体积应变的主要因素可以认为是渗流力与土颗粒间有效应力,其中有效应力变化发挥了关键作用。因而在试验初期有效应力的减小引起了土样的回弹变形,并在回弹变形趋于稳定后才体现出渗流力的作用,即体积应变达到峰值后,先进入短期稳定的阶段,随后缓慢减小。

图9(c)表明,在试验过程中,土样的渗透系数随时间变化趋势与体积应变随时间变化趋势相同,同样经历了类似的3个过程。但相较于体积应变在达到峰值前出现的3次小幅波动,渗透系数在达到峰值的过程中变化相对平稳,整体趋势规律明显。

图10中土样孔隙比与渗透系数的变化关系表明,二者在体积增大和减小阶段的关系曲线基本吻合,其中出现的微小差别可能是土体微观结构变化带来的影响。

4 结 论

(1)随着时间的增加,土样的体积变形经历了先快速增加到峰值,短期稳定后并缓慢减小的过程。此现象与应力路径相关,在施加一定水头给土样后,初期土样内部产生的超孔隙水压力会使有效围压减小,围压卸荷作用进而导致土样产生回弹变形;而后期随着超孔隙水压力的逐渐消散,其产生的回弹效应减弱,变形趋于稳定,仅有渗透力继续作用于土体,使土样体积变形缓慢减小。

(2)开展了不同固结应力作用下土样变形对渗流作用影响的试验,得到了渗流过程中土样体积变化规律。同时得出渗流开始前及稳定后土试样的e-k(孔隙比-渗透系数)关系曲线,对比分析后可知:考虑到变形影响的e-k关系曲线能更好地体现土体的流固耦合效应。

(3)为利用GDS三轴仪高精度特征,对其进行了改装,利用改进后GDS三轴仪的高级加载模块进行渗流与蠕变耦合试验,得到试验过程中体积应变、孔隙比及渗透系数随时间的变化规律,确定了渗流与蠕变耦合动态过程中的e-k关系曲线,水库滑坡流固耦合分析时采用此耦合桥梁更能反映滑坡稳定性的实际情况。