基于虚拟直流发电机的直流微电网惯性提高控制研究

马越超

（包头职业技术学院 电气工程系，内蒙古包头，014030）

0 引言

随着能源危机的加剧，由风能、太阳能、储能组成的微电网成为电力系统中的重要一环。微电网可分为交流微电网、直流微电网和交直流混合微电网。交流微电网由于能更好地适应当前配电网的形式，所以在早期研究过程中，处于领先地位。随着生活中直流负荷的日益增多，直流微电网逐步成为研究热点[1]。但由于直流微电网中各部分均需要通过低惯性的电力电子变换器变流后才能与直流母线相连，故整体缺乏惯性，易受到各种扰动的影响，降低直流母线电压的质量。文献[2]定义了直流微电网惯性时间常数并指出额定电压下电容所存储的能量与扰动瞬间释放的能量成正比关系，存储的能量越大，系统惯性就会越大。但在实际应用中，直流母线上所接电容的容值通常较小，无法在系统受到扰动时，减小直流母线电压变化速率。因此，如何提高直流微网的惯性是一个急需解决的问题。

目前，虚拟惯性控制是提高直流微网稳定性的一个重要策略[2]。文献[3]分析了直流微电网中引入虚拟电容后的惯性提升及其稳定性分析。文献[4]在直流微电网中使用变惯性控制策略，通过直流母线的变化率来灵活改变虚拟电容的容值，从而更好地减小母线电压的变化。文献[5]对交流变换器采用虚拟同步发电机控制，对直流变换器采用虚拟直流发电机（Virtual DC Generator，VDG）控制。

以上的研究结果均对稳定直流母线电压起到了一定的作用。本文以上文献基础上，将VDG 应用到了风力发电的升压变换器中。首先，建立基于VDG 控制的孤岛模式下风储直流微网双级控制策略，分析VDG 对直流母线电压的动态调节过程；其次，对风储直流微电网进行了小信号建模，利用阻抗比判据判断了转动惯量对风储直流微电网稳定性的影响；第三为了合理优化转动惯量，应用了粒子群算法进行寻优；最后在Matlab/Simulink 平台上搭建的风储直流微电网，并给出了风速变化，负载变化这两种工况下的仿真结果，以证明本文所提策略的正确性。

1 风储直流微网结构及原理

图1 为本文构建的孤岛模式下采用虚拟直流发电机控制的风储直流微电网。其由风力发电系统、可控整流、升压电路、逆变器、蓄电池、双向DC/DC 和可调直流负载构成。

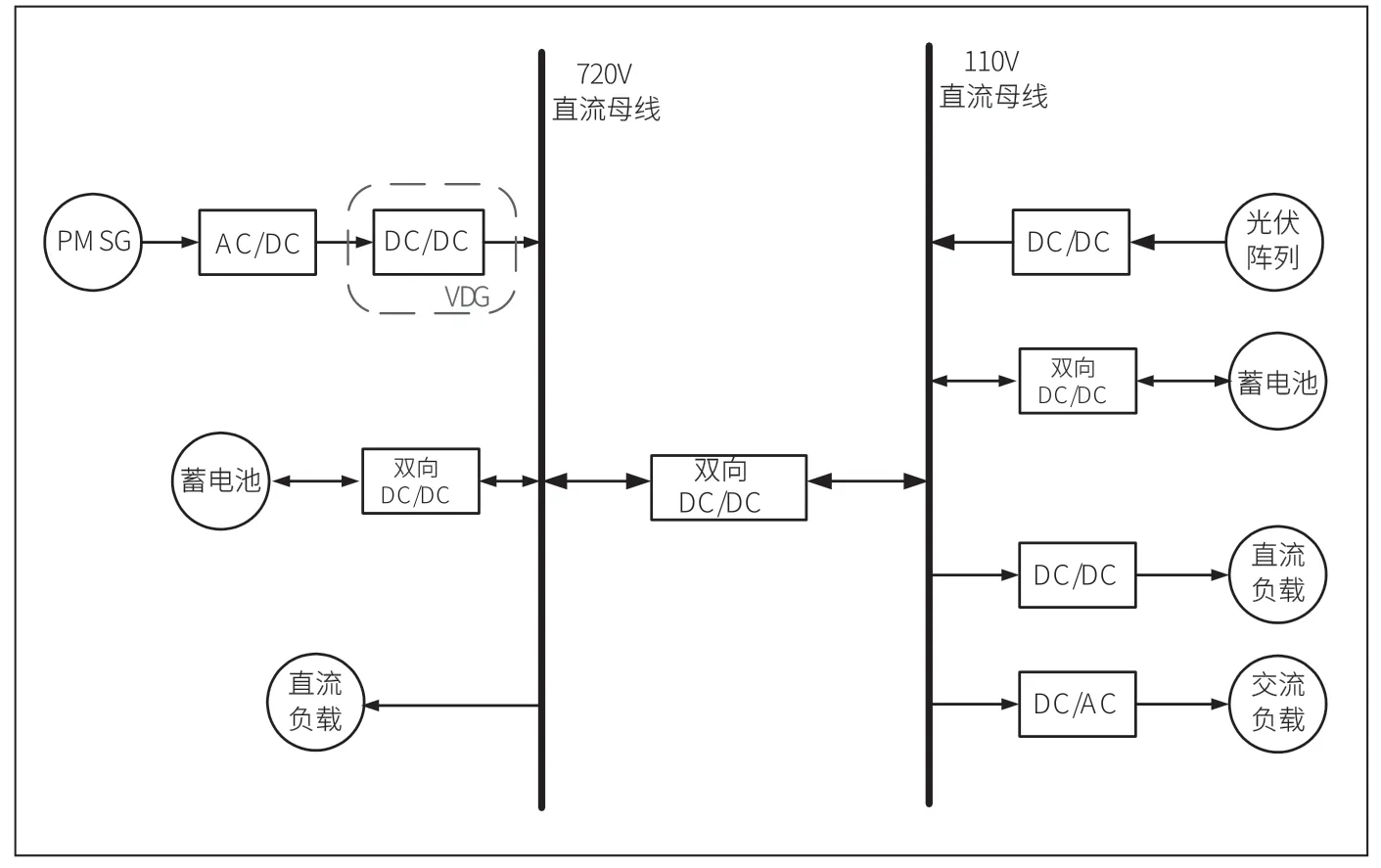
图1 双母线直流微电网控制策略

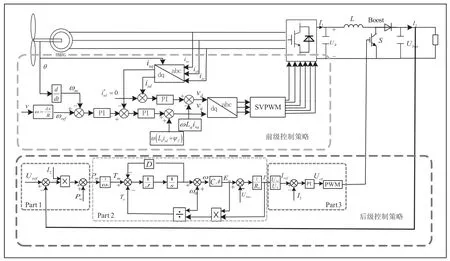
图2 风储直流微电网控制策略

与光伏控制系统相类似，本文设计的风力发电控制系统采用两级式控制策略：第一级为可控整流电路，采用转子磁场定向的矢量变换控制，结合空间矢量脉宽调制（SVPWM）控制技术，其中的转速外环为最大叶尖速比控制方法，使得风力发电系统始终处于最大输出功率状态；第二级为采用虚拟直流发电机控制技术的升压电路，利用虚拟直流发电机来提升前级控制器的输出电压和增加系统的惯性，从而加强风储直流微网的稳定性。

2 基于虚拟直流发电机的风储直流微网控制策略

■2.1 虚拟直流发电机转矩方程建立

虚拟直流发电机在运行时，可以有效地提高系统的惯性。因此，如果用它来控制风机的升压电路（如图3 所示），则变换器此时就会获得与直流发电机一样的机械特性。在使用时，DC/DC 升压电路的端口UB、I1接风机的前级控制电路，端口Ubus、I2接直流母线。

图3 虚拟直流电机模型

虚拟直流电机机械方程可描述为：

式中：J为直流发电机的转动惯量；Dv为直流发电机的阻尼系数；Tm为直流电机的机械转矩，Te为其电磁转矩；ω为实际角速度；ω0为额定角速度；Pe为电磁功率。

结合式(1)(2)可知，由虚拟直流发电机产生的虚拟电磁转矩与直流母线电压提供的虚拟机械转矩是相互制动的。当直流微电网功率平衡时，系统内部不存在功率交换；而当系统功率不平衡时，DC/DC 直流变换器与母线电压就会产生功率交换，也就会导致感应电动势以及电枢电压的变化。

电枢方程可描述为：

式中：E为直流电机电枢电动势；Ia为其电枢电流；CT为其转矩系数；U为机端电压；φ为磁通。

采用以上的虚拟直流发电机控制升压电路时，当发电机所带负载变化时，可以通过改变励磁电流的大小来稳定输出电压，减小电压波动，为系统提供惯性。

■2.2 虚拟直流发电机控制策略

虚拟直流发电机是由三个模块构成：直流电压调节模块、直流发电机模块和电流跟踪模块，具体分析如下：

Part 1：直流母线电压调节模块的主要作用是产生虚拟直流发电机的机械功率Pm。它是由电压补偿环节和风机输出功率两部分构成。电压补偿环节Δp是将直流母线电压的偏差量Δu与变换器输出电流I2相乘后得到的，具体表达式如式(5)所示：

式中：Udref为直流母线参考电压；I2为风机升压变换器输出电流；Pw为风力机输出功率。

Part 2：直流发电机模块主要是得到变换器低压侧电流参考值Ia。其利用机械方程和机械功率Pm计算得到发电机当前转速ω，再由电枢方程得到发电机产生的感应电动势E，从而使得虚拟直流发电机获得与真实直流发电机相同的转动惯量和阻尼系数。

Part 3：直流发电机模块得到的参考电流Ia为变换器低压侧的参考值，而直流母线却并联在了变换器的高压侧，因此为了稳定直流母线电压，必须对其进行电流变换。假设所采用的是理想变换器，则高压侧得到的参考电流通过高压侧的参考值和电流环进而得到变化的PWM 脉冲，从而稳定直流母线电压。

■2.3 风储直流微网动态调节分析

根据式(1)可知，转速ω 可以表达如下：

结合式(6)，可以发现J与ω成反比关系。因此，稳定运行的风储直流微电网在突加负载扰动（负载增加）时的调节过程如下：

其中，PL为负载功率；Uct为脉冲发生器的控制电压；Kpi为电流跟踪模块的PI 调节器的电压放大系数；Ks为PWM 脉冲发生器和DC/DC 升压电流近似电压放大倍数。通过以上的分析可知，虚拟直流发电机的调节主要是通过改变虚拟电动势E的大小，从而来影响Uct并最终实现母线电压的恢复，而且转动惯量J越大，母线电压变化范围就越小。

3 风储微网控制小信号分析

■3.1 升压电路小信号模型

由图1 可建立图4 所示的基于虚拟直流发电机的风机升压变换器小信号模型，相应变换器参数如表1 所示。为了简化分析，本文忽略了该变换器输入电压到电感电流和母线电压之间的传递函数。

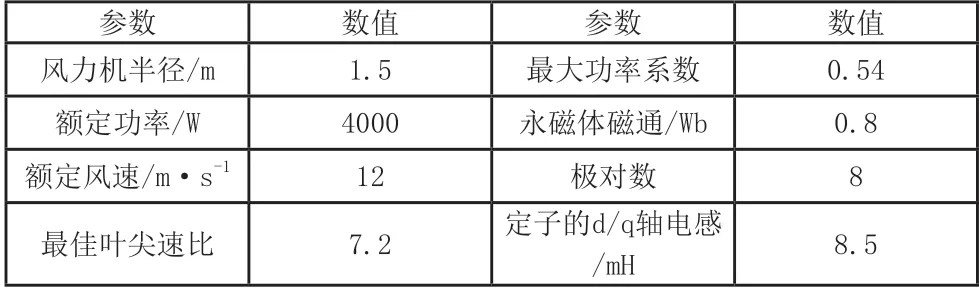
表1 风力发电机主要参数

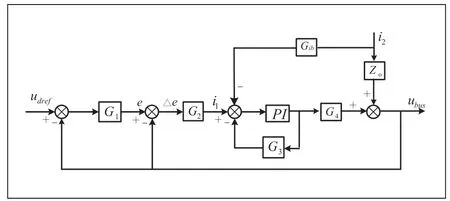
图4 虚拟直流发电机小信号模型

根据图4，可得采用虚拟直流发电机控制的升压电路输出阻抗为：

■3.2 储能变换器小信号模型

同理，由图5 可建立图6 所示的储能变换器在其稳态工作点附近的小信号模型。

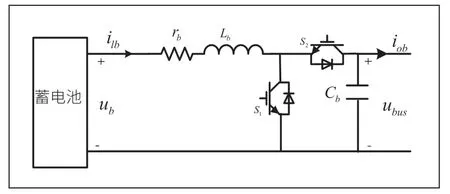
图5 储能双向DC/DC 变换器

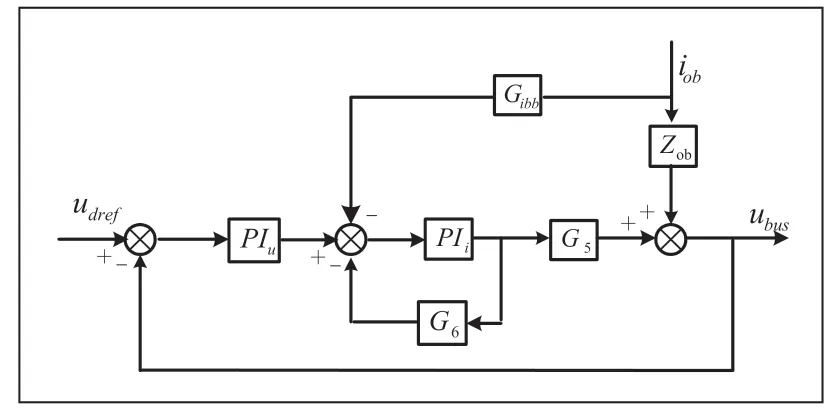
图6 储能系统小信号模型

双向DC/DC 变换器闭环阻抗传递函数为：

■3.3 稳定性分析

根据级联系统的阻抗比判据可知，微源与负荷阻抗比的Nyquist 曲线不进入禁止区时，即可以保证级联系统的稳定性。由以上两式可得，风储直流微电网的阻抗比为：

由式(9)可得，不同转动惯量下的阻抗比Nyquist 图，如图7 所示。从图中可以看出，风储直流微网在转动惯量J变化时，整个系统一直远离禁止区，始终处于稳定状态。

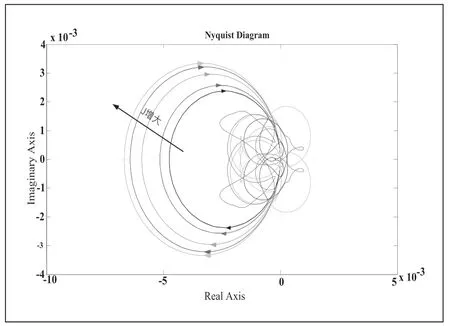
图7 直流微网阻抗比Nyquist 图

4 虚拟直流发电机转动惯量优化

从前文分析可知，转动惯量J 的大小可以影响母线电压的变化范围，但是J 过大也会延长系统的动态响应。因此，为了得到系统的最优性能，必须寻找到使母线电压变化范围最小的转动惯量，也就是最优惯量。为了寻找到最优惯量，本文在Matlab/Simulink 上搭建了基于VDG 的风储直流微电网仿真模型，并在不同的J 值下，得到了一系列母线电压偏差值Δu。以这些数据为基础，利用线性样条（Linear Spine）的方法，建立起以J 为自变量，Δu 为因变量的线性分段函数，如图8 所示。

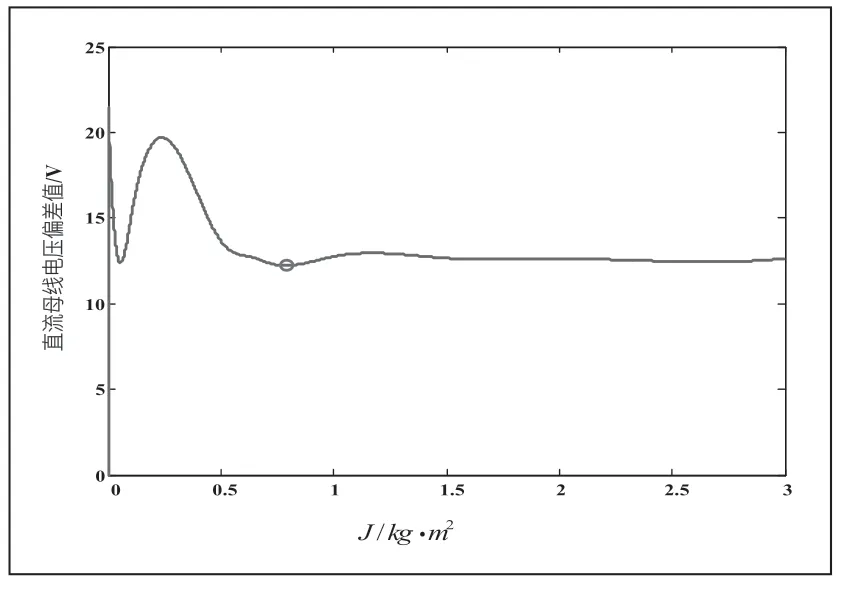
图8 数据插值曲线图

为了得到最优惯量，本文利用粒子群算法进行最小值寻优。由此可得整条曲线的最小值。此时得到的转动惯量最优值为0.789kg·m2，由数据插值曲线得到的Δu 为12.2318V。

5 风储直流微电网控制策略的仿真研究

为了验证本文所提策略的有效性，根据图1，在Matlab/Simulink 环境下搭建有、无虚拟直流发电机控制的风储直流微电网孤岛运行仿真模型，并在风机功率变化、负载变化两种工况下进行仿真。风机及PMSG 部分仿真参数如表1 所示。

■5.1 风机功率变化时的仿真结果

设初始风速为5m/s，0.1s 时风速上升为8m/s，0.2s时突变为12m/s，于0.3s 时下降至10m/s 后维持不变，风速变化如图9(a)所示，对应的母线电压变化如图9(b)所示。由图可知，无惯性控制的系统母线电压将随着风机功率的波动而发生不同程度上的突变。而加入VDG 后的母线电压可以基本维持不变。

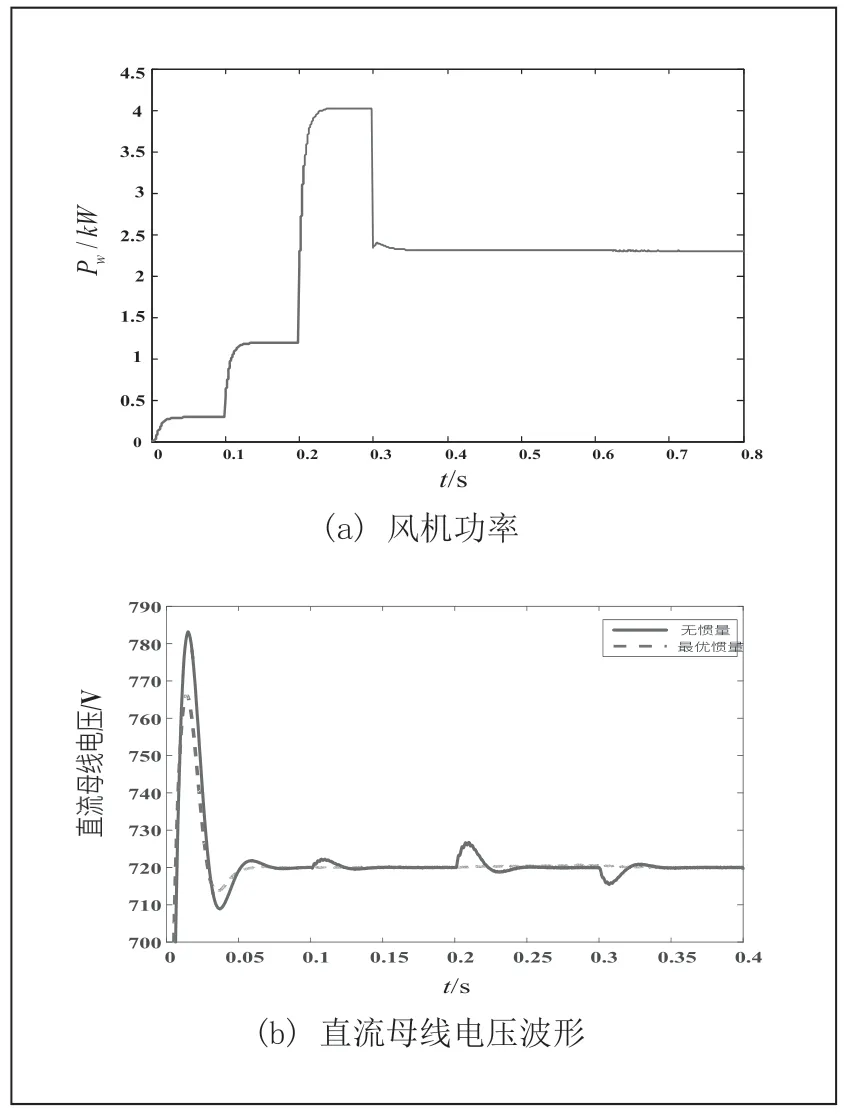
图9 风机功率变化下的仿真波形

■5.2 蓄电池切换次数对比

为维持母线电压稳定，当负载或风速发生变化时，蓄电池将会不断地在充电和放电状态间进行切换。而切换次数过多，将会影响蓄电池的寿命，为提高蓄电池的寿命，需减少其切换次数。图10 为风速和负载变化时，锂电池荷电态SOC 的变化情况。由图可知，未加入VDG 控制的系统，其充、放电切换次数为10 次；而加入VDG 控制的系统，其切换次数则为6 次。

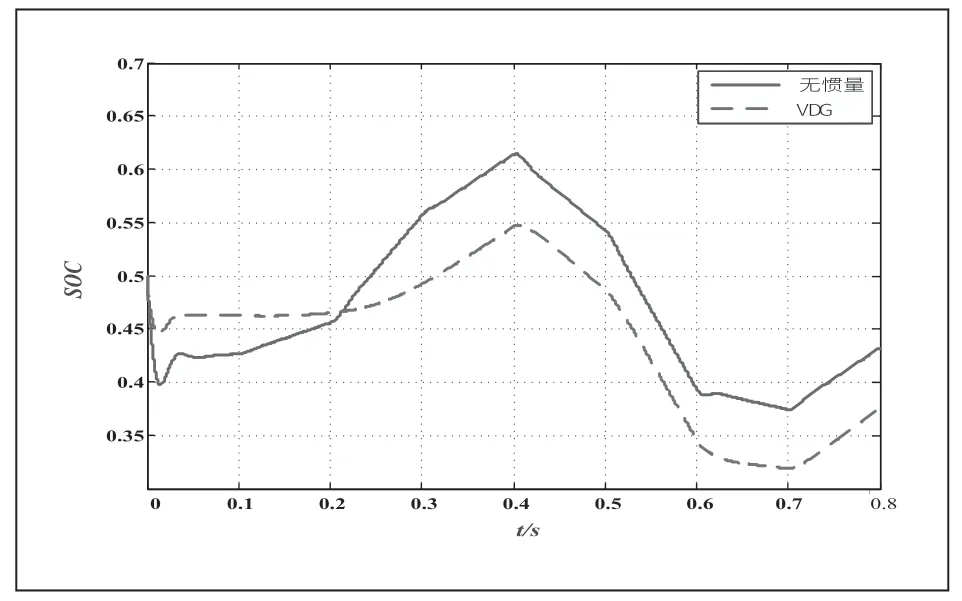
图10 运行过程中SOC 对比图

6 结论

本文将现有的VDG 控制应用到了风储直流微电网的后级变换器中，分析了VDG 对直流母线电压的动态调节过程。应用了阻抗比判据判断了加入虚拟直流发电机控制后的小信号稳定性。通过对系统的仿真，发现VDG 控制可减小直流母线电压的变化范围。利用粒子群算，求解得到的最优惯量可在风速和负载发生变化时有效提高系统的惯性，延长电池的使用寿命，从而实现了整个微电网的稳定运行。