一种基于单片机的模拟量采集滤波算法设计

牛梦毫，周前柏，师璟桐，康颖，杨光

（航空工业西安航空计算技术研究所，陕西西安，710065）

0 引言

模拟量采集功能是嵌入式系统中至关重要的功能，以最具代表性的航空系统为例，航空系统的各子系统例如航电系统、飞控系统、机电系统等通常包括大量的模拟信号，中央管理设备根据这些模拟量转换后的数字信号产生特定的控制输出来实现各个系统不同的控制功能，模拟量采集的精度和可靠性也影响整个机载系统运行的稳定性和可靠性[1]。在嵌入式系统中模拟量采集易受嵌入式系统内部或外部噪声干扰，产生震荡，失真等问题，这极大地影响了嵌入式产品功能以及整个交联系统的鲁棒性。

目前对此问题的解决方法主要为在产品的硬件设计中加入滤波器[2]，加强电磁兼容性设计[3]等，此类方法虽然可以有效滤除部分噪音干扰，但对于小成本嵌入式产品而言这类方法生产成本过高；还有一些方法在产品的软件设计中加入插值滤波[4]，平滑滤波[5]等，此类方法虽然可以有效滤除部分噪音干扰，但也仅适用部分系统平台；本文设计了一种基于STM32 单片机运行的模拟量采集滤波算法，采用较小的成本进行噪声滤除。实验结果表明，本文提出的算法能够较好地滤除噪声干扰，提升了模拟量采集的准确率。

1 傅里叶变换

在数字信号处理领域，傅里叶变换具有非常重要的意义，它可以将复杂的数字信号分解为若干简单数字信号，从而方便选择出有用的信号。

傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

傅里叶变换对于在时空中连续的模拟量信号是适用的，但是此次主要处理对象是已经经过A/D 转换后的模拟量信号并且存储在主存的数字信号，而对于离散信号的变换只有离散傅立叶变换（DFT）才能被适用，对于计算机来说只有离散的和有限长度的数据才能被处理，傅里叶变换和离散傅里叶变换的区别展示如图1 所示。快速傅里叶变换（FFT）也只不过是离散傅立叶变换（DFT）的一种快速的算法。

图1 傅里叶变换与离散傅里叶变换对比

数字计算机采样得到的数字信号，可以进行FFT 变换。N 个采样点，经过FFT 之后，可以得到N 个点的FFT 结果。为了方便进行FFT 运算，通常N 取2 的整数次方。

快速傅里叶变换算法预设采样频率为Fs，信号频率F，采样点数为N，经过快速傅里叶变换算法的变换结果就是一个为N 点的复数向量组，其中返回的每一个点就对应着一个频率点大小，该点的模值即为该频率值下的幅度特性。

快速傅里叶变换算法假设原始信号的峰值为A，那么返回结果除了第一个点直流分量之外的每个点的模值就是A的N/2 倍。每个点的相位可以认为是在该频率下的信号的相位。第一个点表示直流分量，即表达该点频率为零，而第N+1 个点则表示采样频率Fs，这中间被N-1 个点平均分成N 等份，每个点的频率依次增加。假设某点n 所表示的频率为：Fn=(n-1)*Fs/N。Fn 所能分辨到频率为Fs/N，如果采样频率Fs 为512Hz，采样点数为512 点，则可以分辨到1Hz。512Hz 的采样率采样512 点，刚好是1 秒，也就是说，采样1 秒时间的信号并做FFT，则结果可以分析精确到1Hz，如果采样5 秒时间的信号并做FFT，则结果可以分析精确到0.2Hz。要提高频率分辨率，则必须增加采样点数，也即采样时间。频率分辨率和采样时间是倒数关系。

上述大致介绍了快速傅里叶变换的思想与使用，本文将使用快速傅里叶变换与其逆变换作为本文所设计软件算法的主要组件，以及分析软件滤波与硬件滤波相比的优势与不足。

2 模拟量采集滤波算法设计

本文所提出的模拟量采集滤波算法运行在stm32 型号的单片机上，是基于经典的模拟量采集电路设计的，该电路包括了用于采集模拟量输入的信号调理电路，用于采集并将模拟量转换为数字信号的A/D 转换芯片，以及用于控制以及与A/D 转换芯片通信的FPGA 芯片。为了能够较好地验证该软件算法的实际效果，系统硬件电路实现减少了部分滤波措施，实验所用系统的结构图如图2 所示。

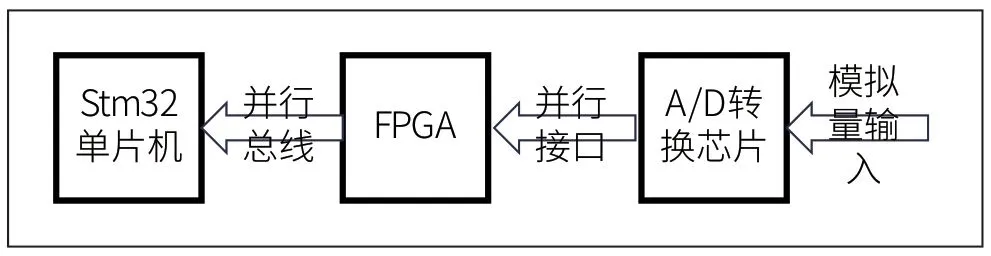
图2 系统结构图

该嵌入式系统中为了避免成本过高，体积过大，并以实现小型化、轻量化的设计思路为指导，多路开关电路可根据模拟量采集数量，PCB 面积选择合适模拟开关电路，此处系统设计选择4 路多路开关，通过FPGA 逻辑控制切换通道采集，没有一对一采集设计需求。采集模拟量采集信号首先输入进A/D 转换芯片，并由A/D 转换芯片转换为数字信号输入给FPGA，暂存在FPGA 的寄存器堆中，最后由stm32芯片周期性读取并记录。

考虑到系统本身的噪声输入，算法优先对该模拟量的模拟地进行测试，作为后续模拟量输入采集的比较基准。本文设计模拟量采集滤波算法由STM32 芯片执行，算法流程如图3 所示。

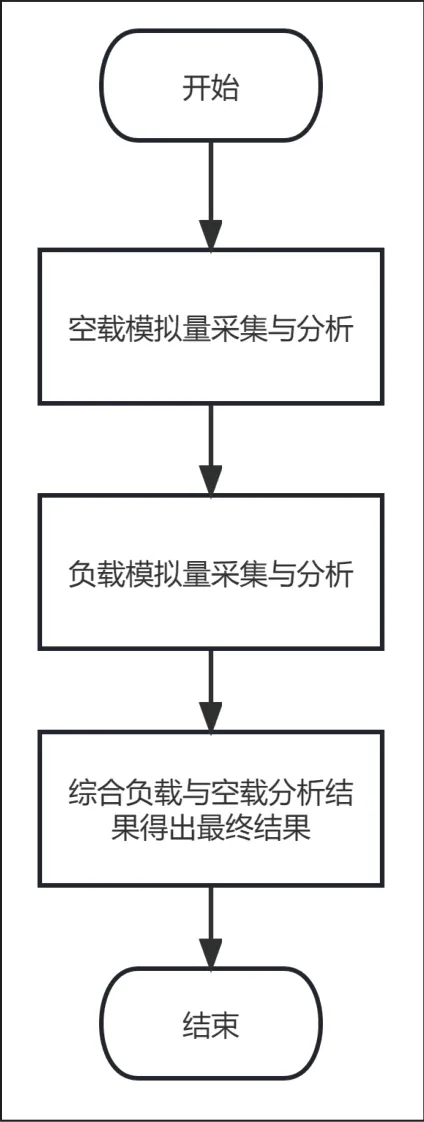
图3 算法流程图

（1）在系统对应模拟量接口空载情况下，STM32 芯片发送指令给FPGA，采样频率为1024Hz，采集1024 个模拟量样本点，并对采集到结果进行快速傅里叶变换，并将采样结果记为Zx。

（2）在系统对应模拟量接口负载情况下，STM32 芯片发送指令给FPGA，采样频率为1024Hz，采集1024 个模拟量样本点，并对采集到结果进行快速傅里叶变换，并将采样结果记为Zy。

（3）对最终量Zx-Zy 进行快速傅里叶逆变换，得到重构后的样本值，即为滤波后的采样信号，并对其滑动滤波后求取平均值，作为此次模拟量采集参考值。

其中该算法中使用的滑动滤波算法使用滑动窗口大小为64，步长为32，其该算法流程如下：

（1）对采集到的1024 个模拟量按照时序记录并选择64 个样本点求取平均值，并依时序向前滑动16 个样本点的步长，重复此操作，直到无法向前滑动，将该步骤得到结果记为A1；

（2）对A1 中64 个经过初步滤波的样本点选择8 个样本点求取平均值，并依时序向前滑动8 个样本点的步长，重复此操作，直到无法向前滑动，将该步骤得到结果记为A2；

（3）对A2 求取平均值，所得到的结果即为此次滑动滤波结果。

选择滑动滤波算法由于滑动滤波能够更有效地滤除尖峰信号，其示意图如图4所示。

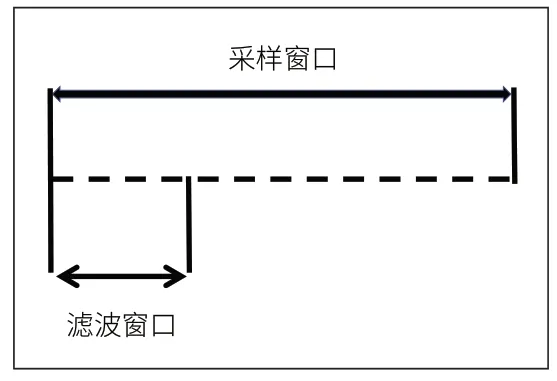
图4 滑动滤波示意图

关于该算法中一些关键参数的选择问题进行说明：选择STM32 的采样频率1024Hz，采样点1024 个主要为了快速傅里叶变换由时域信号转换为频域信号后分辨率为1Hz，这样可以让快速傅里叶变换与快速傅里叶逆变换的内存开销在4MB 级别，可以适配较多嵌入式系统的内存容量，而且在MHz 级别的主频单片机上可以将响应时间控制在1s～5s 之间，不会导致过长的系统延迟；滑动滤波算法中滑动窗口64 和步长16，滑动滤波算法本质是对该时间序列进行一维卷积操作，窗口大小即为卷积核的大小，如果卷积核尺寸过小则滑动滤波会退化为求取平均值滤波，一般根据经验公式而言，假设序列长度为N，则滑动窗口选择在N1/2到2 倍N1/2之间。

3 实验验证与结论

为了验证该滤波算法的有效性，搭建了具有复杂电磁干扰的系统运行环境，并选择以下两种方法作为参考对照：

（1）STM32 芯片对FPGA 采集的数据不做任何处理，直接作为此次模拟量采集的参考值，下文简称方法a；

（2）STM32 芯片发送指令给FPGA，采样频率为1024Hz，采集1024 个模拟量样本点，但仅对这些样本点做平滑滤波后取平均值，作为此次模拟量采集的参考值，下文简称方法b。

特此说明，本文所提出的模拟量狭义指代的是电压输入，电流输入，电阻输入，频率输入等模拟量信号，而所有模拟量输入信号在硬件输入形式的本质只有两种：即电压输入与电流输入，因此本文只选取了最具代表性的电压输入与电流输入作为此次模拟量滤波实验的验证项目。

电压信号与电流信号作为最基本两种模拟量信号，本质上是电路中的电磁场信号的变换，所以任何系统内部或外部的电磁场扰动都可能会对这两种模拟量信号产生干扰，但是一般情况下这些噪声相对于电路系统中的基准电压都非常小，基本可以忽略不计。但是如果系统外部存在一个强电磁干扰源，例如大功率用电设备，就可能会对系统的输入接口上产生一个较强扰动，从而影响该输入电路的正常工作。本文在设计验证实验时反向利用了此特点，方法即为将该嵌入式系统的模拟量输入接口从嵌入式系统的引脚引出，另一端连接一个微型天线结构的铜制导体，这些端口可以将附近环境中的电磁扰动以较大功率传输到嵌入式系统的内置输入接口电路上；而后本文将实验环境选择在有8 台200W 以上的大功率用电设备周围，用这些大型设备的关断来模拟外部电磁干扰的强度。并且为了模拟电磁干扰信号的随机性，会选择在实验中随机开启或关断一些设备，制造一些电磁扰动的尖峰，来观察本文所设计的模拟量滤波算法是否具有鲁棒性。

实验选择0V 电压，5V 电压，0A 电流，2A 电流作为4路模拟量输入信号，负载端为恒流恒压源，实验记录5 次模拟量采集结果，实验结果如表1 所示。

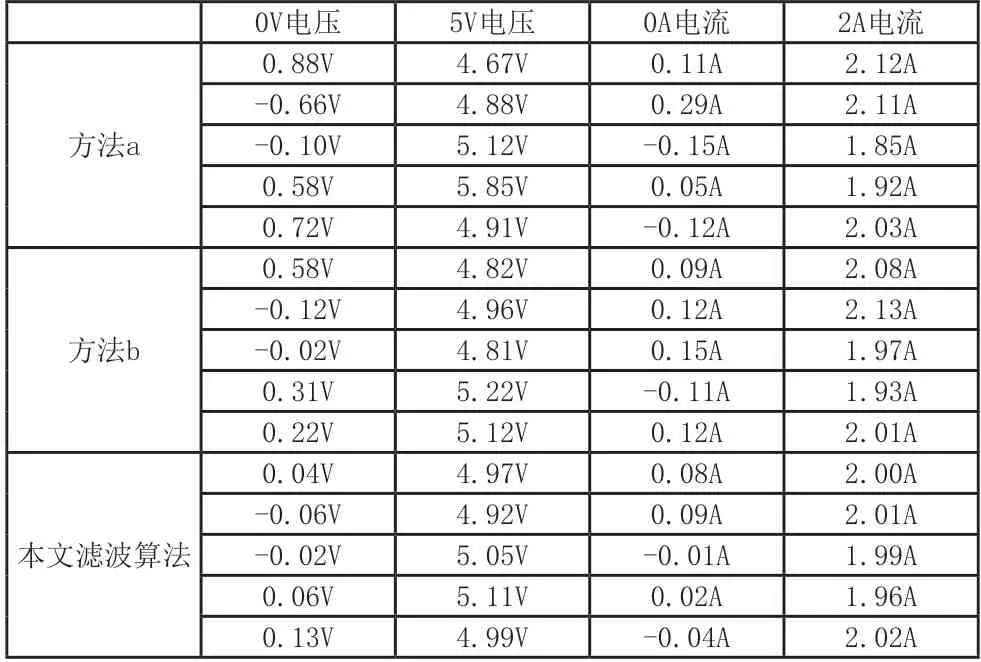
表1 实验结果表

从实验结果可以推知，本文所提出的滤波算法能够有效滤除噪声尖峰，以及噪声的直流分量；而且对比方法b，该算法能够更好避免模拟量超差问题。

本次实验虽然验证了本文所提出的模拟量采集滤波算法相较于平滑滤波算法能够更好的滤除噪音，但依然存在对噪音尖峰超差的问题，这也从一定层面反映了仅依靠软件滤波的局限性，在对于较大的尖峰，浪涌等噪声信号的滤波上一般硬件滤波具有更明显的效果，所以为了追求更强的安全性与可靠性，未来应该追求软硬件有机结合的滤波方式，采取一定体系化，系统化的滤波设计，应该作为此类工作将来的一个重要方向。

4 结语

本文提出了一种基于STM32 单片机的模拟量采集滤波算法，该算法虽然在一定程度解决了模拟量输入采集的精度问题，但是该算法依然存在很多改进的空间。从时间复杂度和空间复杂度来看，方法a 的时间复杂度为O(1)，空间复杂度为O(1)；方法b 的时间复杂度为O(n)，空间复杂度为O(n)；本文所提出算法的时间复杂度为O(n2)，空间复杂度为O(n2)，如果为了获得更好的滤波效果而将n 值取得过大，将会极大地占用嵌入式系统的内存资源，并且会对系统响应的实时性造成影响。未来工作的主要方向就是对该算法空间复杂度与时间复杂度的优化。