基于指数趋近律的机械臂神经网络滑模控制

王国刚，孙德炜，金红娇，孙其龙

（吉林化工学院 信息与控制工程学院，吉林吉林，132022）

0 引言

机械臂已经成为工业控制领域中的不可或缺的工具。由于机械臂是一个非线性、强耦合、时变的系统，并且存在未建模动态、参数变化、外部扰动及摩擦等 各种不确定因素的影响。这些不确定因素会导致机械臂各关节跟踪精度变差，因此使机械臂具有良好的动态性能具有重要的研究意义，设计控制器以实现机械臂能快速、稳定地跟踪期望轨迹是机械臂控制的核心问题。在实际工程中，机械臂系统存在建模不确定性以及受外界干扰等诸多复杂因素的影响，专家学者在解决这个难题的同时，也在机械臂的轨迹跟踪方面取得了重大突破[1～4]。诸多学者提出过各种的控制方法，主要有PD 控制，滑模控制，计算力矩控制，模糊滑模控制等[5～8]。文献[9]对传统干扰观测器进行优化，反馈补偿外界干扰的同时利用神经网络的万能逼近特性，提高响应速度和轨迹跟踪精度；文献[10]为解决由于系统存在建模不确定性以及外界干扰对控制结果造成的不良影响，提出一种学习系统不确定性的未知上界的自适应神经滑模控制方法，以此来提高系统的控制性能；文献[11]针对滑模控制中存在的收敛速度和系统抖振两个方面的问题，通过分析两种类型趋近律的优缺点，设计一种对系统抖振能够有效控制的同时也能提升收敛速度的改进型滑模趋近律；文献[12]提出了一种采用自适应神经网络补偿包括建模不确定性和外部干扰在内的系统不确定性的滑模边界控制器，以将关节驱动到所需位置并快速抑制振动。文献[13]针对机械臂系统的滑模控制存在抖振的问题，提出了一种变指数趋近律滑模控制律，仿真结果表明该控制策略可以有效抑制抖振：文献[14]针对一种并联机械臂提出了鲁棒PID 控制策略，通过选择合适的PID 控制器增益，使系统达到稳定的状态。

针对机械臂跟踪精度和稳定性等问题，本文对基于神经网络滑模控制做出优化与改进，相比于上述文献，本文对机械臂系统的整体性控制有了进一步的提升。考虑到对机械臂动力学模型进行建模时，存在不确定项以及外部干扰。对此本文先利用神经网络对建模的不确定项进行逼近，然后采用基于指数趋近律的滑模控制用以削弱系统的抖振、提高系统的控制性能。

1 动力学模型

考虑n关节机械臂动力学方程［15～16］如下：

其中，q∈Rn为关节角位移量，M(q)∈Rn×n为惯性矩阵，C(q,)∈Rn为离心力和哥氏力项，G(q)∈Rn为重力项，F()∈Rn为摩擦力项，τ∈Rn为控制力矩，τd∈Rn为外加干扰以及系统建模的误差项，利用RBF 神经网络对其进行处理。

2 基于RBF 神经网络的滑模控制器设计及其稳定性分析

由于在实际控制系统中存在的干扰因素较为复杂。例如，系统摩擦力，系统建模误差以及外界干扰等都会影响到系统的轨迹跟踪。

RBF 神经网络结构简单，收敛速度快，能够较高精度地逼近任何连续非线性函数，结构采用并列处理机制，具备较强的容错能力等优势，其主要的工作机理为系统实际的控制参数经隐含层激活函数的非线性变换后，通过权值的线性相加传递至输出层。其中隐含层中的激活函数为径向基函数，结构特点为径向中心对称且两边衰减过渡，输入的数据距离中心越近，输出越敏感。基于RBF 神经网络能够以任意精度逼近未知函数的特点，RBF 神经网络能够较好地满足存在不确定性的系统控制的需要要求。

在设计控制系统时，我们需要将上述的不确定项利用RBF 神经网络进行估计，然后对整个系统采用滑模控制为控制器。以此来提高机械臂轨迹跟踪精度和稳定性。

控制系统的原理如图1 所示。

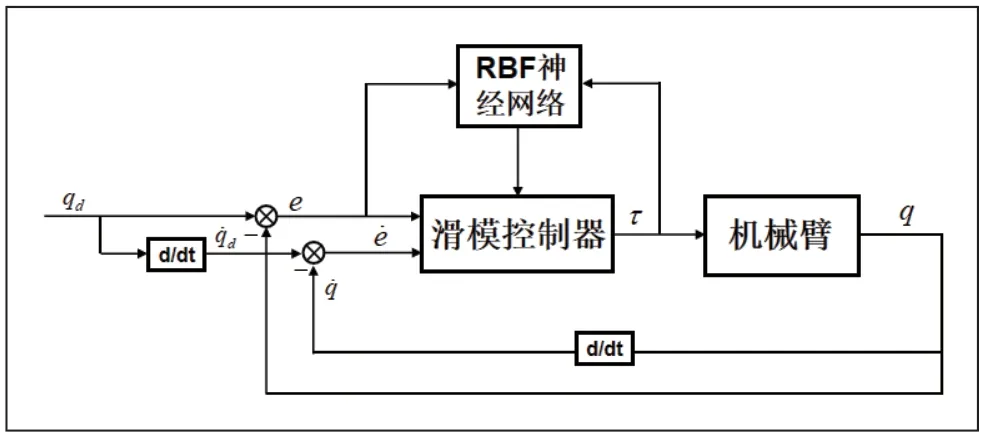
图1 控制原理

采用基于RBF 神经网络的滑模控制对机械臂进行位置的轨迹跟踪控制。设qd为q的期望值，为的期望值。跟踪误差为：

定义滑模函数为：

滑模动态特性保证了系统的稳定性和状态收敛到平衡状态e=0。结合式(2)和式(3)，可得：

滑模控制具有响应快、对干扰不敏感等优点。但是由于滑模控制自身特性原因，使其存在抖振现象，并且该现象无法被控制系统消除。

选取合适的趋近律可以实现在相同的控制抖振下更快的趋于零或在相同收敛速度下削减抖振。为削减抖振现象，本文采用基于指数趋近律的滑模控制。

式中，-ks是指数趋近项，k越大，-εsgn(s)趋近滑模面速度越大，-εsgn(s)是等速趋近项，可消减抖振。增大k的同时减少ε可保证快速趋近的同时消减抖振。

高斯基函数具有良好的解析性，用于理论分析时比较方便，其图像不仅光滑性好而且还是径向对称的。应用RBF神经网络时可以从一定程度上使系统的跟踪性能更好，并且其自适应调节能力更强。因此，RBF 神经网络控制机械臂的不确定性问题、跟踪问题以及稳定性问题是有意义的，结合机械臂的动力学特性，利用RBF 神经网络控制机械臂，进而提高系统性能，实现快速收敛。同时RBF 神经网络技术可对机械臂动力学方程中未知部分进行逼近，由此提高了对机器人的控制精度。

RBF 神经网络结构如图2 所示。

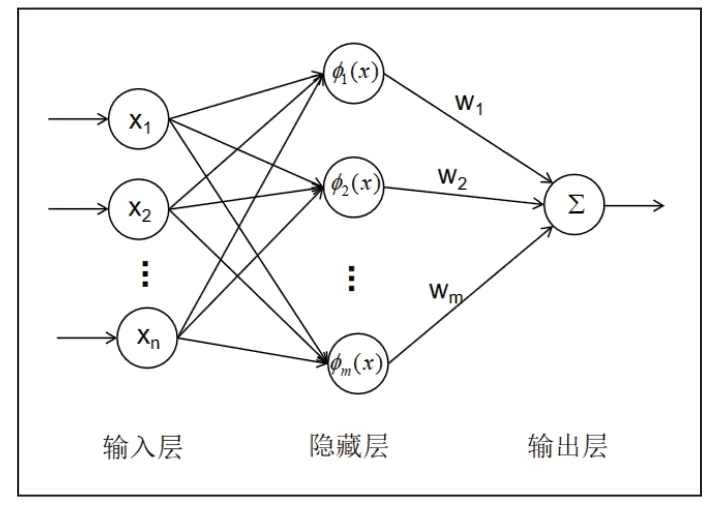
图2 神经网络结构

根据RBF 网络自身特性，采用RBF 神经网络逼近不确定项f，网络算法为：

其中，x为网络的输入，j为网络隐含层第j个节点，为神经网络高斯基函数输出，W*为网络理想权值，ε为网络的逼近误差，ε≤εN。

则RBF 神经网络的输出为：

将式(1)与式(4)进行联立可得：

在实际工程模型中的f项是未知的，然后对f进行逼近。为RBF 神经网络的估计值。

取：

为实现自适应逼近定义神经网络自适应律：

为更好的抑制滑模控制带来的抖振，本文采用了指数趋近律来实现滑模控制。由式(9)和式(5)可知：

将指数趋近律式(5)与式(12)结合得到控制器：

上式中，v为鲁棒项。将其设为：

定理1：针对机械臂动力学系统式(1),设计了滑模函数式(4)，并在自适应律式(11)下得到系统的控制器方程式(13)，保证了跟踪误差的有限时间内收敛。

对于整个系统控制器取式(13)，自适应律取式(11)。定义Lyapunov 函数为：

将式(13)代入式(9)中，可得：

将式(17)代入式(16)中，可得：

所以系统渐进稳定。

3 仿真实验

在对滑模控制算法的研究和稳定性分析完成后，为进一步证明该控制算法的可行性，采用MATLAB 搭建机械臂控制系统来对该控制算法进行仿真验证。

选用的机械臂示意图如图3 所示。

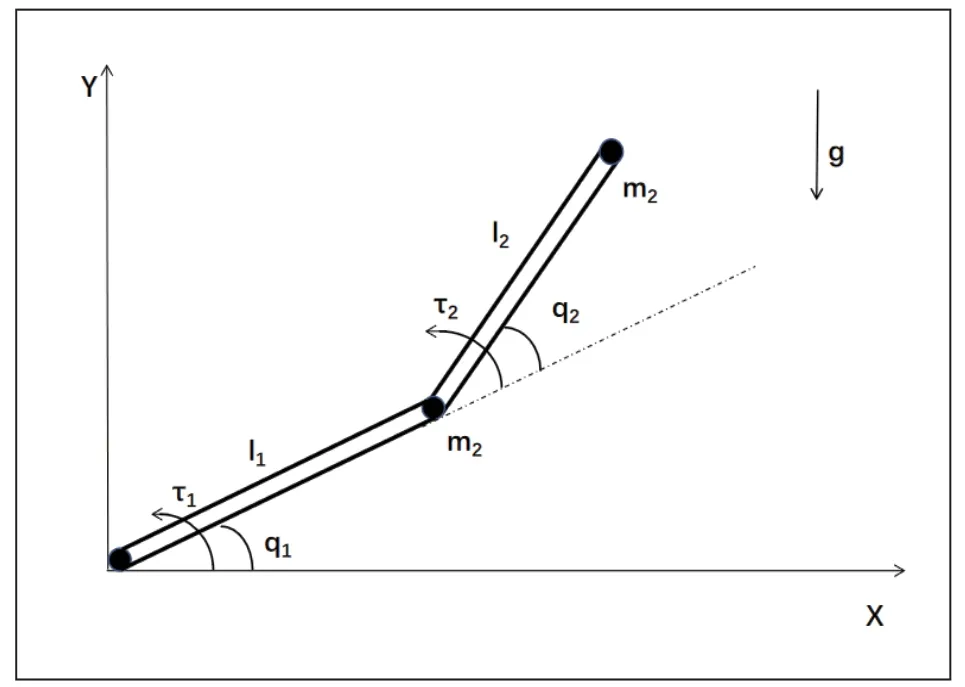
图3 双关节机械臂

动力学参数为：

机械臂的物理参数值见表1。

表1 物理参数

以机械臂动力学模型为被控对象来验证所提方法有效性，控制器见式(15)。系统的两个关节的指令分别为qd1=cos(πt)，qd2=sin(πt)，初始状态为[0.050 -0.050]，在鲁棒项中，取bd=0.20，εN=0.30，同时取F=diag[100,100]，Λ=diag[12,12]。RBF 神经网络的网络结构为5-7-2，网络输入取x=，高斯基函数的中心点cj为[-1.5,-1,-0.5,0,0.5,1,1.5]，高斯基函数的宽度为bj=18，仿真结果如图4～14 所示。

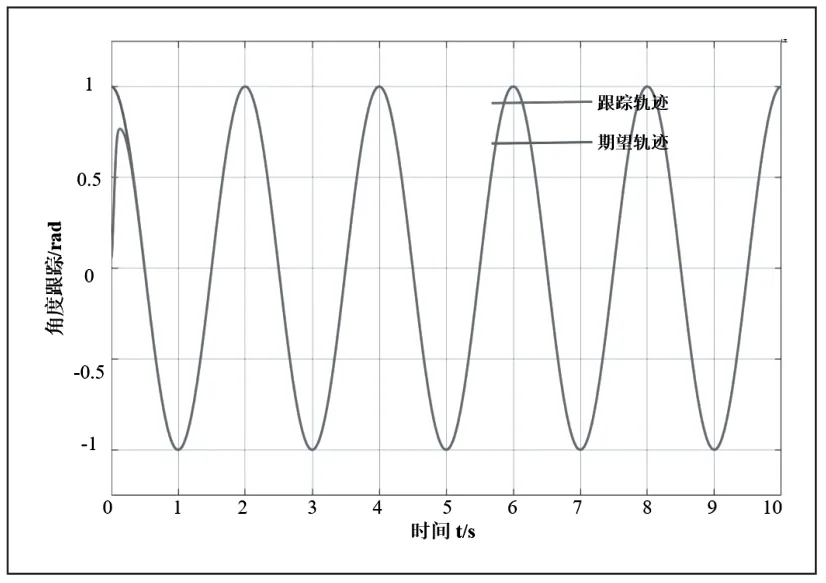
图4 关节1 角度跟踪

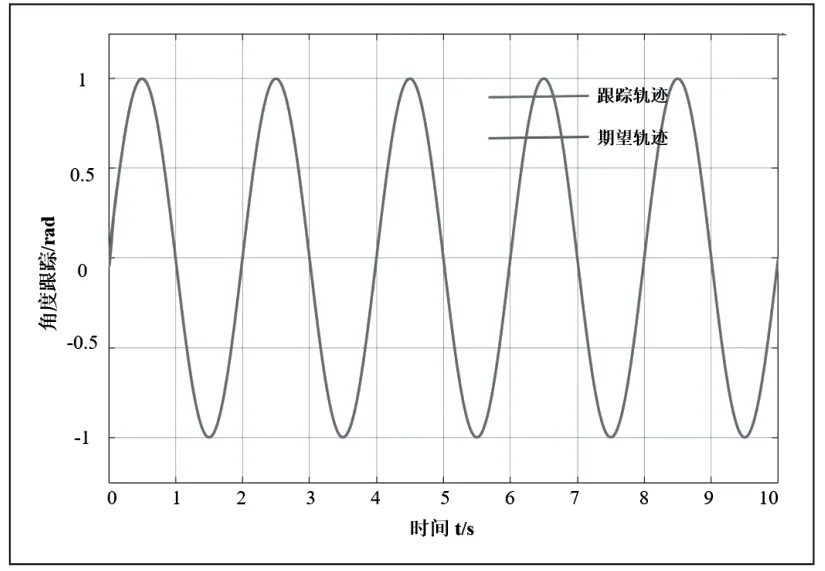
图5 关节2 角度跟踪

4 总结

本文在为解决机械臂轨迹跟踪精准度、稳定性等问题时，对基于神经网络滑模的控制方法做出优化与改进。提出了一种基于指数趋近律的神经网络滑模控制算法。对仿真结果进行分析与总结。

由图6 及图7 可知，角度跟踪误差最高不超过1rad，并且在约0.5s 后角度跟踪误差曲线波动极小，轨迹跟踪曲线与期望轨迹几乎重合。由此可以说明该控制算法有较好的轨迹跟踪性能；由图10 和图11 可知，在约0.5s 前关节1角速度跟踪误差达到11rad/s，关节2 的角速度跟踪误差约为1.5rad/s，随后图像急速削减，无限趋近于零。所以可知本文提出的控制算法也具有良好的角速度跟踪效果，有效地抑制了系统的抖振问题。仿真结果表明该控制算法具有较好的轨迹跟踪效果的同时也具有良好的稳定性和快速性。

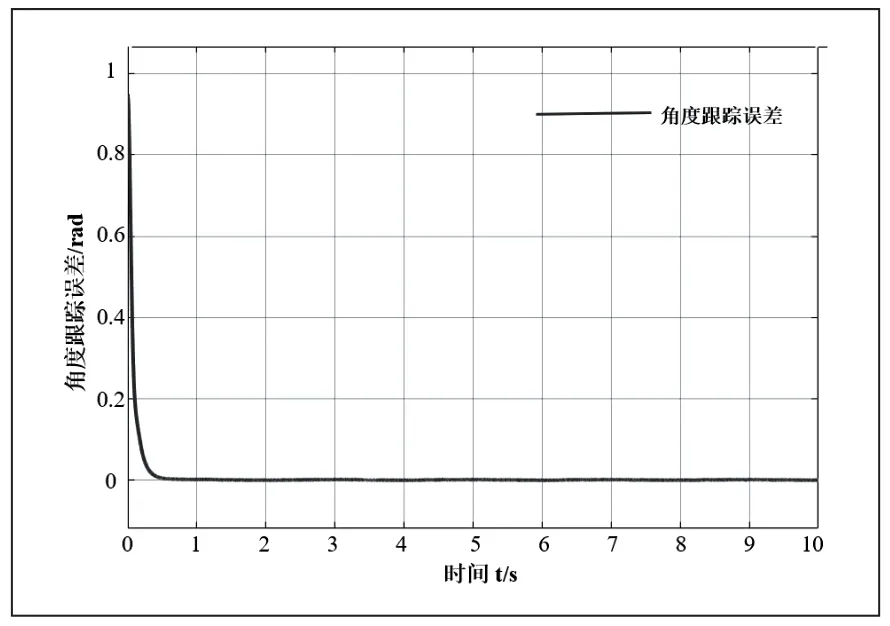
图6 关节1 角度跟踪误差

图7 关节2 角度跟踪误差

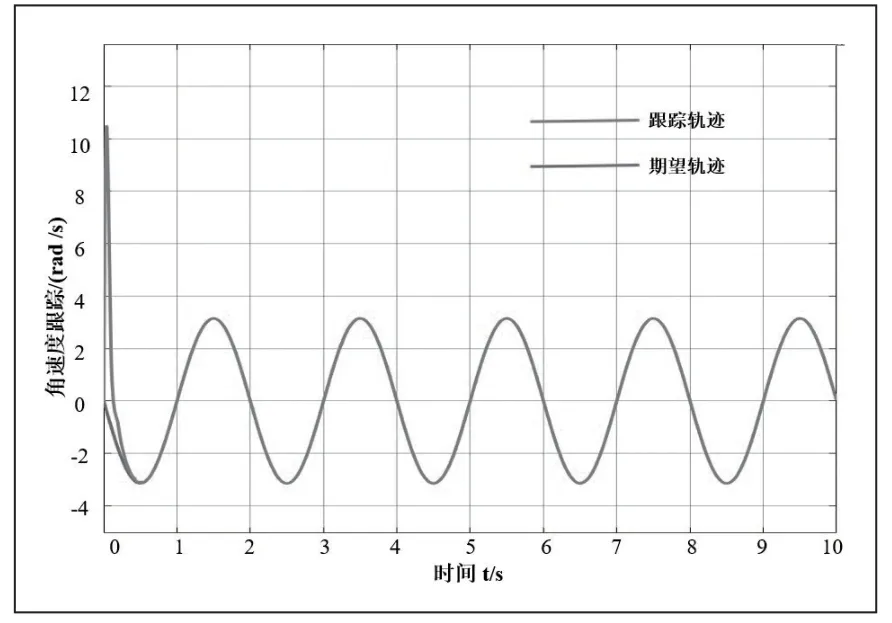
图8 关节1 角速度跟踪

图9 关节2 角速度跟踪

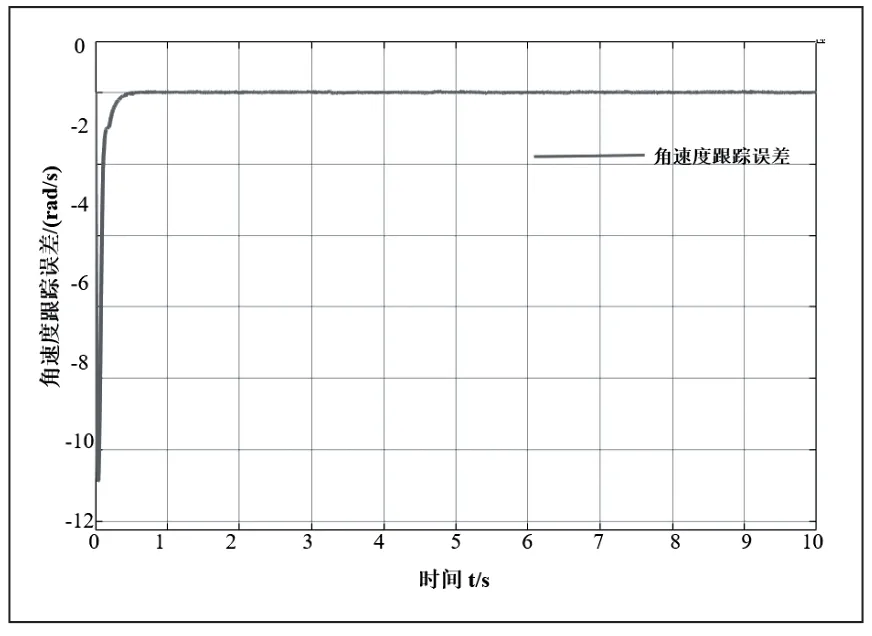
图10 关节1 角速度跟踪误差

图11 关节2 角速度跟踪误差

图12 关节1 控制输入

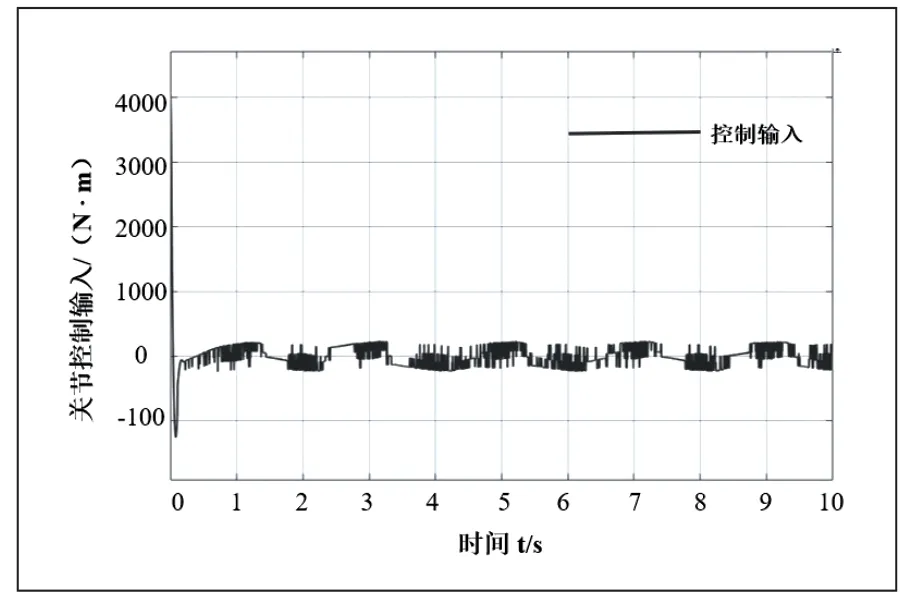
图13 关节2 控制输入

图14 关节1 及关节2 的 ||f (x)||及其逼近||(x)||