严格对角占优矩阵的预条件Jacobi迭代法

许云霞，雷学红

许云霞，雷学红

（凯里学院 理学院，贵州 凯里 556011）

1 引言及预备知识

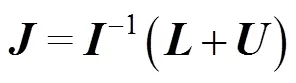
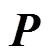
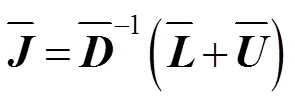
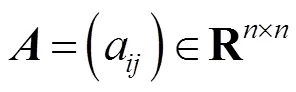
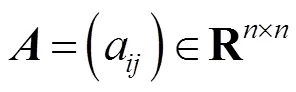
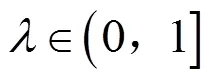
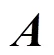
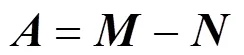
2 主要结果及证明

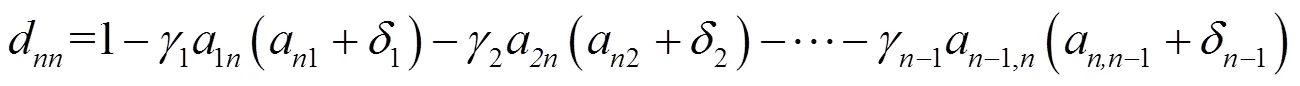
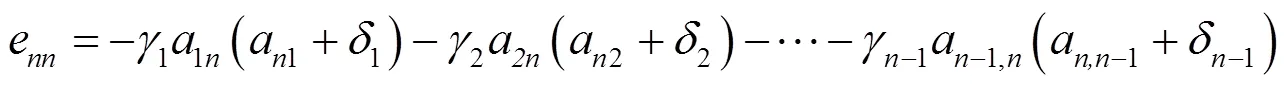
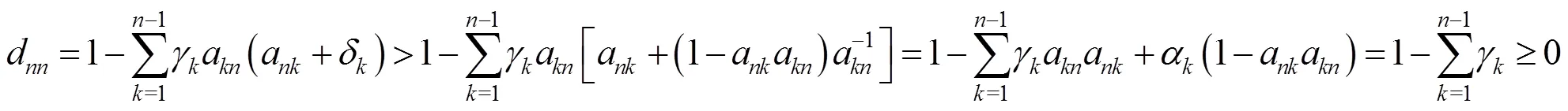
3 数值实例

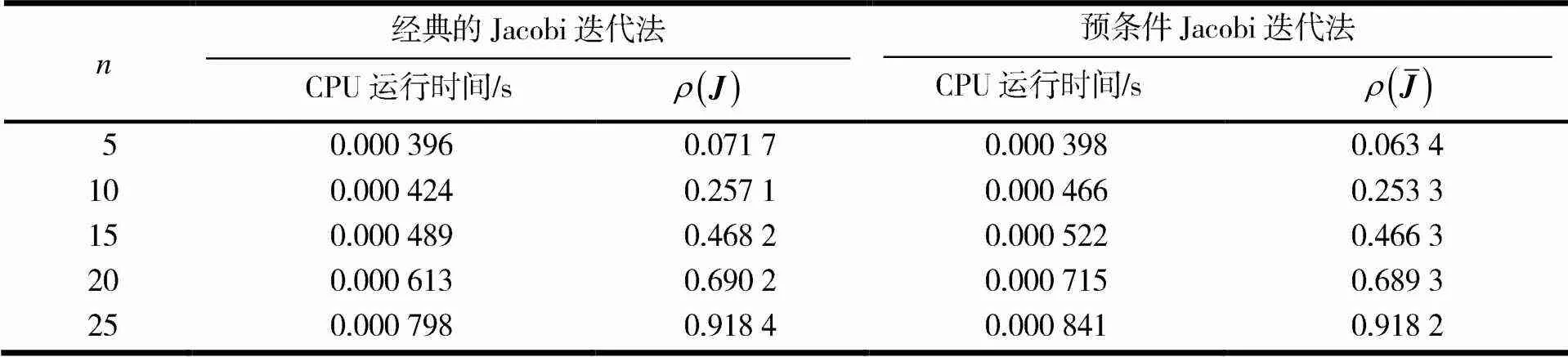
表1 经典的Jacob迭代法和预条件Jacobi迭代法的CPU运行时间和谱半径

由表2可以看出，随着矩阵的阶数增大，所用时间增加，谱半径也随之增加. 因为预条件Jacobi迭代法增加了预条件子与系数矩阵的乘积运算，因此预条件Jacobi迭代法的运行时间比经典的方法要多. 同时预条件的引入使得所提出的预条件Jacobi迭代法的谱半径小于经典的Jacobi迭代法[10]的谱半径，显然本文所提出的预条件Jacobi迭代法收敛速度比经典的Jacobi迭代法的收敛速度稍微快一些.

[1] 谷同祥，安恒斌，刘兴平，等．迭代方法和预处理技术：上[M]．北京：科学出版社，2015．

[2] 王转德．迭代矩阵的谱分析[D]．成都：电子科技大学，2009．

[3] 雍龙泉. 线性方程组的4种迭代方法[J]．陕西理工学院学报（自然科学版），2016，32（5）：80-84．

[4] 李爱芹．线性方程组的迭代解法[J]．科学技术与工程，2007，7（14）：3357-3364．

[5] Berman A，Plemons R J．Nonnegative Matrices in the Mathematics Sicences[M]．SIAM：Philadelphia，1994．

[6] 徐树方，高立，张平文．数值线性代数[M]．2版．北京：北京大学出版社，2013．

[8] 陈景良，陈向晖．特殊矩阵[M]．北京：清华大学出版社，2001．

[9] LI Wen，SUN Weiwei．Modied Gauss-Seidel type methods and Jacobi type methods[J]．Linear Algebra and Its Application，2000，317：227-240．

XU Yunxia，LEI Xuehong

（School of Science，Kaili University，Kaili 556011，China）

O151.21

A

10.3969/j.issn.1007-9831.2024.01.001

1007-9831（2024）01-0001-04

2023-05-28

2023年度凯里学院校级规划课题（2023XJGHYB11，2023XJGHYB09）; 贵州省教育厅青年科技人才成长项目（黔教合KY字[2019]189号，黔教合KY字[2019]186号）

许云霞（1980-），女，河南开封人，副教授，硕士，从事数值代数研究．E-mail：xuyunxia321@163.com