冲击下铁的各向异性对晶界附近相变的影响*

张学阳 胡望宇 戴雄英

1) (湖南工程学院计算科学与电子学院,湘潭 411104)

2) (湖南大学材料科学与工程学院,长沙 410082)

1 引言

由于铁在人类社会中,特别是在国防和工业领域扮演着重要的角色,因此,铁在动态高压下的行为一直是研究的热点问题之一,其中α → ε 马氏体相变尤其受到人们的关注,首次实验研究早在1956 年就被发表了[1].之后,人们开展了一系列关于铁的冲击加载的研究,特别是动态加载下铁的塑性活动和相变的实验研究[2–4],引发了关于相变和塑性相互影响的诸多讨论[5–11].但是,由于动态高压实验的瞬时性,研究人员应很难得到动态细节,计算机模拟则补充了实验研究所欠缺的细节,逐渐成为了主流的研究方法之一.其中,分子动力学(MD)模拟基于原子间相互作用势直接模拟材料的结构演化,不需要构建复杂的物理或力学模型,可以提供冲击下微观结构的动态变化细节.但是,长久以来没有合适的势能够在模拟中重现出铁在冲击加载下的塑性过程,因此动态加载下铁的塑性和相变的耦合一直是MD 研究的盲点.直到最近几年,一些新开发的势克服了这一缺陷,特别是Wang等[12]开发的MAEAM 势不仅成功模拟相变前的塑性,还克服了相变产物中有很多面心立方相变后的(FCC)原子的缺点(实验中已经证明FCC 结构不会大量出现).这些为研究冲击下铁的相变与塑性耦合的微观细节奠定了基础.

很早就有研究发现,冲击加载下的相变与塑性都喜欢在缺陷附近形核[13],之后人们陆续开展了很多关于缺陷对相变与塑性影响的研究[14–17].晶界作为自然界中最常见的缺陷,其对相变与塑性的影响自然也受到了人们极大的关注.例如Zong 等[18]研究了钛的晶界在冲击下对相变的影响,并且提出共格孪晶界对钛的α → ω 相变是有利的.对于铁的MD 研究来说,前期人们因为缺乏合适的势函数,只能把研究的重点都集中在相变上,后来Gunkelmann 等[19–21]和Wang 等[22–24]在分别开发了适合动态高压下铁的势函数之后,都在第一时间研究了冲击加载下铁的相变与塑性的耦合问题.Gunkelmann 等[25]指出在晶界附近位错先于相变形核,且可以在模拟中观察到明显的三波结构,同时测得的相变压力阈值高于静态下.而Wang 等[24]发现晶界能够通过影响相变与塑性的耦合从而改变相变的机制,并提出新的机制与实验中观察到的缺陷诱导机制的特点相符,人们对多晶内相变与塑性耦合的认识有了很大的进步.但是,模拟中多晶的响应会受限于晶粒的尺寸,使得对晶界附近相变与塑性的认识还不够清晰,而双晶模型可以突破这个限制.因此,我们在早些时候就采用了双晶模型来研究晶界如何影响相变以及塑性,总结了典型晶界对相变形核的重要影响[26,27].但是晶界的种类十分丰富,除了经常被研究的典型晶界,还存在很多的研究几乎没有涉及到的普通晶界,而这些晶界附近的冲击响应是否会符合已有的认知目前是不清楚的,因此关于晶界对相变与塑性影响的认知还不完善,有待于进一步研究.

在以往的关于材料的冲击加载MD 研究中,活塞法等产生的冲击波普遍被近似为一维冲击波,冲击方向以外的应力分量对冲击响应的影响被完全忽视.此外,MD 研究中讨论的常见冲击晶向都是中心对称的,例如〈001〉,〈110〉和〈111〉对于体心立方结构(BCC)和面心立方结构(FCC),〈0001〉,〈1010〉和〈1210〉对于六方密排结构(HCP)[28–30],而沿非中心对称晶向冲击的研究是罕见的.那么,非常见晶向在动态冲击加载中的表现是否一直都是可被忽略的呢? Zhakhovsky 等[29]的研究指出冲击波的结构与晶体的晶向有密切的联系,因此关注沿非中心对称的晶向冲击的过程其实也是有必要的.对此我们研究了沿非中心对称晶向冲击单晶铁的过程[31],发现选取非中心对称晶向为冲击方向时,冲击波不能再被简单视为一维的,晶格的各向异性在冲击过程中有明显的影响,甚至会影响相变路径的选择.考虑到多晶中晶向的随机性和多样性,显然晶向的各向异性在多晶的冲击加载中将会产生更重大的影响,只不过没有引起人们足够的重视而已.此外,在设计双晶模型研究不同晶界对相变的影响的时候,发现某些模型中的晶界附近的行为与我们预期的完全不同,联系到上述我们关于沿非中心对称晶向冲击的研究,晶格的各向异性很有可能是导致其反常的重要因素.本文的重点就是基于上述现象讨论冲击加载下铁的各向异性如何影响双晶模型中的晶界附近的相变.

综合上述,虽然已经对铁的冲击响应过程做出了一定的探索,但是还有很多问题有待于人们去揭示,例如晶格的各向异性在冲击加载中的影响就没有引起足够的重视,关于冲击加载下晶向的各向异性的研究还有待进一步开展.基于此,本文主要研究了冲击下包含对称晶界的双晶模型中非常规晶向对晶界附近相变的影响.由于多晶取向的随机性和合金中各种原子对中心对称性的破坏,本文能够为多晶和合金的冲击实验提供一定的理论支持.

2 计算方法

使用Lammps 软件[32]模拟了包含对称晶界的双晶铁模型在冲击加载下的非平衡分子动力学过程,之前的研究已经证明MAEAM 势[22]在研究冲击下的铁的相变与塑性的问题上有很大的优势.所构建的模型如图1 所示,模型1 沿X,Y和Z方向的尺寸分别为19.74 nm,19.90 nm 和162.81 nm,晶体取向分别为〈100〉,〈031〉和〈013〉.模型2 沿X,Y和Z方向的尺寸分别为20.23 nm,20.13 nm 和151.45 nm,晶体取向分别为〈110〉,〈332〉和〈113〉.这两个模型所包含的原子数都超过了500 万,且测试结果表明模型的尺寸是足够的,不会有边界效应的影响.模型弛豫的方法如下: 首先,使用共轭梯度法使模型的能量处于最小化;然后,将样本的初始条件设置为等温等压系综(NPT),样品的温度设置为10 K,较低的初始温度可以消除噪声的影响,使得图像更加清晰,而且经过测试发现样品初始温度为室温的模拟结果与10 K 的差异很小,表明设置较低的温度不会影响本文的结论,对于X,Y和Z的边界采用周期性边界条件,将模型置于上述条件下弛豫20 ps;最后,将弛豫好的模型Z轴方向的边界条件改为非周期性边界条件,并且将系综改变为微正则系综(NVE)后,进入冲击加载阶段.弛豫阶段的时间步长为1 fs,冲击阶段的时间步长为0.5 ps.冲击波由活塞法产生,并沿Z轴从左向右扫过模型,还对比模拟了冲击波在同样的模型中沿Z轴从右向左扫过的过程,排除了两侧微观结构不严格对称造成的影响.本文使用的可视化工具为Ovito[33],依据维里应力计算方法计算应力[34].通过将模型沿Z轴切片来统计模型速度和应力张量等[35].本文中的c轴为垂直于HCP 晶胞的正六边形底面的向量,模型中大量相变产物的c轴需要通过我们自主开发的微结构分析程序来确认,其简要思路是先通过Ovito 软件筛选出属于HCP 结构的原子并保留,循环选取其中的每个原子作为中心原子,通过原子间的距离找出中心原子的12 个最近邻原子,找出12 个最近邻原子中与中心原子处于同一个平面的6 个原子,并求解该平面的法线向量,即为c轴.

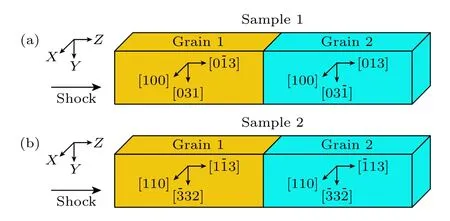
图1 模型示意图 (a) 包含sigma5 晶界的模型1;(b) 包含sigma11 晶界的模型2Fig.1.Model schematic figures: (a) Model 1 containing sigma5 grain boundaries;(b) model 2 containing sigma11 grain boundaries.

3 结果与讨论

3.1 对称sigma5 晶界两侧的不对称响应

在关于冲击加载下晶界附近相变的研究中[26,27],对称晶界两侧的响应几乎都是空间对称的,例如在沿垂直于晶界的方向冲击时,对称sigma5〈100〉扭转晶界、sigma〈110〉倾侧晶界、sigma〈110〉扭转晶界以及共格孪晶晶界两侧的相变产物和相变路径都是相同的,尽管由于反射波的影响,晶界左侧的响应稍微“弱”于右侧.上述冲击响应满足空间对称性与晶界两侧微观结构的对称保持一致(如图1所示),然而发现有些对称晶界的冲击响应是不对称的,如图2 所示.图2(a)是包含sigma5 晶界的模型1 在冲击加载下某个时刻的微观结构图,代表HCP 结构的红色原子是相变发生后的主要产物,该晶界两侧在受到冲击后的响应有着明显的差异,即右侧有较多的HCP 原子,而左侧观察不到HCP原子的存在.而且随着模拟时间的增加,左侧也不会发生相变,我们还通过模拟更长模型的冲击来确认了这一点.该结果表明,晶界两侧的相变阈值存在一定差异.晶界左侧因为有反射波的影响,因此左侧的冲击响应比右侧要“弱”一些是可以预期的,但是反射波引起的差异应该是十分有限的,模型1中晶界两侧相变阈值的差异不能用反射波来解释.图2 还展示了模型1 同时刻的剪切应力和温度的分布,可以看出,冲击波到达的所有区域中,波前左侧的区域1 是剪切应力最高的,对应这一区域的结构正在发生弹性形变.区域1 左侧是区域2,与区域1 相比剪切应力较低,对应该区域的结构发生了塑性形变,塑性过程会释放剪切应力.区域3 对应着相变区域,发生了相变的区域剪切应力达到最低,因为相变过程中有大量原子发生滑移,原子间的滑移能够进一步释放剪切应力.根据上述剪切应力与形变过程的对应关系可以判断,区域4 是没有发生相变的,这与图2(a)呈现的微观结构是相符的.根据图2(c)温度分布可知,塑性行为是引起温度上升的主要原因,温度最高的是上述各区域的边界以及晶界,对应冲击加载下这一部分原子拥有最高的活跃度.

图2 冲击加载下含sigma5 晶界的模型1 在24 ps 时刻的(a)微观结构图,红色表示HCP 结构的原子,蓝色表示BCC 结构的原子,绿色表示FCC 结构的原子,白色代表无序原子,晶界的位置可以通过观察白色原子的位置得到;(b)剪切应力分布图;(c) 温度分布图Fig.2.(a) Microstructure figures of the model 1 containing sigma5 grain boundaries under shock loading at 24 ps,where red represents HCP structure atoms,blue represents BCC structure atoms,green represents FCC structure atoms,and white represents disordered atoms,the position of the grain boundaries can be obtained by observing the position of white atoms.(b) The shear stress distribution;(c) the temperature distribution.

3.2 对称sigma11 晶界两侧的不对称响应

为了研究影响晶界两侧的响应差异的因素,还模拟了含sigma11 晶界的模型2 的冲击响应过程,如图3 所示.图3(a)表明模型2 中晶界两侧的响应也是不对称的,右侧的相变产物多于左侧.经过对微观结构的分析发现,晶界两侧相变产物的类型也是不一样的,需要进一步分析导致晶界两侧相变产物存在差异的原因.据目前已有的研究,不同的相变模式下相变路径、相变过程以及相变的产物都有很大的差异,而目前最常见的两种相变模式为应力援助模式[26]和应变诱导模式[27].应力援助模式的特点: 压缩过程中能量累积到能克服相变的势垒时开始发生相变,相变发生较慢.应变诱导模式的特点: 多发生在缺陷附近,缺陷附近非常规的局域结构可作为相变的核,因此相变阈值低,相变开始较快.根据图3(a)可知,晶界左侧的相变符合应力援助模式的特点,而右侧的相变符合应变诱导模式的特点.图3 还展示了模型2 冲击加载下的剪切应力和温度的分布情况,与图2(b)不同的是晶界右侧没有塑性形变区(图2(b)中的区域2),即剪切应力减小的相变区与弹性形变区直接相邻,这表明晶界右侧的晶格不需要被压缩太多就可以开启相变.而且,模型2 晶界右侧的相变阈值要明显低于左侧,右侧相变的这些特点也是符合缺陷诱导模式的.晶界左侧由于有反射波的影响其剪切应力的分布较为复杂,但是整体比晶界右侧要高,这对应于左侧的相变阈值高和相变产物少.

图3 冲击加载下含sigma11 晶界的模型2 在20 ps 时刻的(a) 微观结构图,颜色标示同图2(a);(b) 剪切应力分布图;(c) 温度分布图Fig.3.(a) Microstructure of the model 2 containing a sigma11 grain boundary under shock loading at 20 ps,and the color marking is the same as that of Figure 2(a);(b) the shear stress distribution of the model 2;(c) the temperature distribution of the model 2.

为了进一步确认晶界两侧的相变模式,分析了晶界两侧相变产物的c轴和相变动力学.图4 是BCC 结构转变至HCP 结构的示意图,左侧是BCC结构的一组原子,右侧是HCP 结构的一组原子,选取的原子相变后刚好组成HCP 晶格的一个晶胞.BCC 晶格要转变至HCP 晶格需要两个过程,一是晶格沿〈001〉方向压缩,对应原子2 和3 的距离减小,同时原子1 和2 之间的距离小幅度地增加.二是相邻层的原子之间发生相对滑移,在图4中滑移即黄色原子相对紫色原子整体移动.相变需要这两个过程结合起来,但是这两个过程的时序却不是固定的,比如说,在缺陷诱导模式相变过程中,由于有缺陷帮助形核,相变阈值较低,压缩与滑移过程几乎同时进行,而应力援助模式相变过程中,由于需要靠压缩积累相变的能量来克服势垒,因此滑移落后于压缩开始的时刻,模型2 中晶界两侧相变的差异将会对照上述两种相变模式的特点来讨论.图5(a)和图5(b)分别展示了模型2 中所选取的晶界两侧附近的HCP 晶胞,通过c轴的定向来确定相变前后的晶向关系.经分析图5(a)中晶界左侧晶胞的c轴与模型中X,Y和Z轴的夹角分别约为90º,25º和125º,与模型2 晶界左侧晶体中的晶向几乎一致;而图5(b)中晶界右侧晶胞的c轴与X轴一致,即与晶界右侧晶体中的[110]晶向一致,由此可知,相变后晶界两侧HCP 晶胞的c轴是不对称的.通过观察图5 中两个晶胞的形态也可以得到相变后晶界两边晶胞的c轴是不对称的,即两边经历了不同的转变路径.

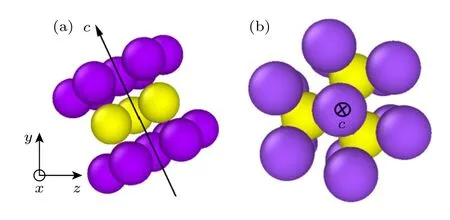
图5 模型2 中sigma11 晶界两侧发生相变后分别选取的一个HCP 晶胞的原子形貌图 (a) 左侧;(b) 右侧Fig.5.Atomic morphology of an HCP cell selected after phase transition on both sides of grain boundary in model 2:(a) On the left;(b) on the right.

为了了解晶界两侧相变动力学的差异,追踪了晶界两侧原子转变过程中的位置.图6 中的晶格参数a,b和r的定义对应于图4:a是原子2 和3 之间的距离,a减小可表征转变过程中晶格的压缩过程,b是原子1 和2 之间的距离,r是原子1 和4 之间的距离比上原子2 和4 之间的距离,r的变化则可以表征原子4 等黄色原子相对于紫色原子的滑移过程.图6(a)和图6(b)分别展示了模型2 中晶界两侧的相变过程中a,b和r随时间的变化,图中p点表示晶格受到冲击后压缩至最大值附近的时刻,s点表示相邻层的原子滑移过程开启的时刻.从图6 可知,晶界左侧的p点与s点之间存在一个时间差,即相变过程中压缩开始一段时间后才开启滑移过程,而右侧的p点与s点几乎同时出现,表明两个过程几乎同时发生.上述结果表明右侧滑移发生的时刻要明显早于左侧,这对应于前面讨论过的右侧有更低的相变阈值.联系前面两种不同的相变模式对应压缩和滑移过程不同的时序,左侧的规律符合应力援助模式,右侧的则符合缺陷诱导模式.至此,从多个角度证实了模型2 中晶界两侧的相变存在着很大的差异,结合模型1 的讨论可以得出,对称晶界两侧在受到冲击时确实存在着不对称的响应.

图6 展示了冲击过程中晶界两侧的晶格参数(lattice parameter)随时间的变化 (a) 对应晶界左侧;(b) 对应晶界右侧.图中a 和b 已经被归一化处理了Fig.6.Variation of lattice parameters on the (a) left and(b) right sides of grain boundaries over time during the shock process,where a and b have been scaled.

3.3 晶格的各向异性对晶界两侧的影响

为了探究影响对称晶界两侧不对称响应的原因,关注了晶界两侧在冲击波到达后未发生相变的时刻.选取一组沿Z轴均匀分布的原子,记录其冲击过程中在X,Y轴方向的坐标与初始坐标的偏差,模型1 中所选取的原子在t=12 ps 时的位置偏差如图7(a)所示.从图7(a)可知,原子在X轴方向相对于初始位置没有移动,而在Y轴方向冲击波扫过区域的原子都有了不同的偏移.活塞法产生的冲击波普遍被近似为一维冲击波,因此很少关注冲击波在垂直于冲击方向的X和Y轴方向产生的影响,图7(a)表明“一维冲击波”在晶体内传播时对垂直传播方向的X和Y轴方向也有不可忽视的影响.在图7(a)中,冲击过程中原子只在Y轴上有移动,模型1 的X轴为〈100〉晶向,Y轴为〈031〉晶向,根据BCC 晶格的特点,晶格关于〈100〉晶向是对称的,而关于〈031〉晶向是非对称的,这表明原子在受到冲击时在X和Y轴方向不同的表现与其是否是对称晶向有关.

图7 活塞速度为0.5 km/s 的加载下,模型1 在12 ps 时内部原子的(a)位置偏差和(b)剪切应力随时间的变化Fig.7.Time dependent variation of (a) position deviation and (b) shear stress of atoms in model 1 under loading with a piston speed of 0.5 km/s at 12 ps.

图7(a)中晶界两侧的原子在Y轴方向的移动幅度并不是相等的,这对应晶界两侧的剪切应力有较大的差异.图7(b)展示了模型1 在12 ps 时的剪切应力的分布,这个时刻冲击波已到达晶界,但是晶界处还没有发生相变,因此研究此时晶界两侧的差异对于理解两边不同的响应有重要的意义.从图7(b)可知,晶界两侧附近的剪切应力都低于离晶界较远的区域,但是晶界右侧的剪切应力明显低于左侧,这对应模型1 中晶界两侧只有右侧发生了相变.在模型2 中,因为晶界右侧发生的是缺陷诱导模式相变,相变速度较快,因此捕捉不到冲击波到达但相变未开始的图像,所以将活塞速度降低至0.2 km/s,该冲击强度下晶界两侧都不会发生相变,这样可以排除相变对晶界两侧剪切应力的影响.图8 对应模型2,与图7 类似,所追踪的原子在冲击下也只在Y轴方向有移动,Y轴对应的〈332〉晶向是非对称的,X轴的〈110〉晶向是对称晶向.而且图8 中晶界两侧移动偏差和剪切应力的差异与模型2 在冲击加载下晶界两侧不一样的相变过程的联系也是类似于图7,这表明移动偏差的差异与该方向的晶向是否对称有密切的联系,即冲击的晶向是影响晶界两侧发生不对称相变的重要原因.

图8 活塞速度为0.2 km/s 的加载下,模型2 在17.5 ps 时原子的(a)位置偏差和(b)剪切应力随时间的变化Fig.8.Time dependent variation of (a) position deviation and (b) shear stress of atoms in model 2 at 17.5 ps with a piston speed of 0.2 km/s.

之前研究了沿非中心对称的晶向冲击时单晶铁的响应,发现X轴和Y轴方向对应的晶向是否对称对相变路径的选择产生了重要的影响[31],结合本文的研究可以得到铁的各向异性对其冲击响应有重大的影响.特别是,之前的研究发现晶格的各向异性的影响并不只存在于铁的模拟中,而是广泛存在于BCC 晶格金属的冲击加载中,因此晶格的各向异性对冲击加载下相变的影响应该得到进一步的重视.

4 结论

本文利用分子动力学方法模拟了冲击加载下对称晶界两侧不对称的响应过程,结论如下:

1)有对称微观结构的晶界两侧存在着不对称的冲击响应,本文中的具体表现为模型1 中sigma5晶界两侧的相变阈值存在较大的差异,而模型2中sigma11 晶界两侧的相变阈值和相变路径都存在着较大的差异,特别是该晶界两侧不同的相变动力学表明晶界两侧触发了不同的相变模式,即应力援助模式与缺陷诱导模式;

2)冲击下两个模型中的原子都会沿Y轴方向偏移,这表明沿非中心对称晶向冲击时,活塞法产生的冲击波不应该再被简单视为一维的;还发现冲击下原子在垂直于冲击方向的X和Y轴上是否偏移与晶向的对称性密切相关,并且在有偏移时晶界两侧的偏移是不一样的,这对应晶界两侧的剪切应力分布也是不对称的,剪切应力的差异最终导致晶界两侧的相变阈值和相变模式出现差异.综上所述,对称晶界两侧的冲击响应与晶向的对称性密不可分,因此晶格的各向异性是造成晶界两侧不对称响应的重要因素.