基于改进PSF估计的车载复杂图像复原

吴春林，王正家，朱永平，何飞宇，白锦瑞

(1.湖北工业大学 机械工程学院，湖北 武汉 430068；2.湖北省产品质量监督检验研究院，湖北 武汉 430068)

0 引言

在相机传感器拍摄的曝光时间内,场景与摄像机发生相对运动产生的模糊为运动模糊[1]。运动模糊会使车载图像出现模糊现象,影响图像的清晰度和质量。模糊的车载图像会导致目标边缘轮廓不清晰,降低图像识别的准确率,观察者出现乏力和不适等感受,无法掌握路况信息,增加交通事故的风险,因此需要对车载运动图像进行复原。图像运动模糊复原技术是图像处理领域的一个重要分支[2],其研究涉及信号处理、图像处理、数学等多个领域的交叉,对图像处理领域的发展和进步起到推动作用。

根据图像中模糊的范围将运动模糊分为全局运动模糊和局部运动模糊。全局运动模糊是整幅图像模糊,只有一个模糊核;局部运动模糊是仅有部分区域模糊,其他区域清晰。目前全局运动模糊去除方面取得了一定的成就[3-6],且效果较好。但是运动模糊不只有全局运动模糊,采用全局运动模糊复原的方法对局部模糊图像处理时,会产生严重的振铃效应,且图像质量下降严重,所以学者们针对局部模糊图像进行了研究,取得了较大的成果。文献[7]基于再模糊理论对图像进行再模糊,结合图像的模糊前后奇异值的特点,提取出模糊区域;文献[1]结合多尺度的奇异值特征和闭合型图分割的方法得到模糊区域,对模糊区域提取并复原,再与清晰区域拼接完成局部运动模糊的复原。虽然上述的局部运动模糊复原方法都取得了不错的效果,但是针对图像中同时拥有局部运动模糊和全局运动模糊的复杂图像,这些方法都不适用。文献[8]把局部运动模糊和全局模糊进行分离,取得了一定的效果,将运动物体所在的矩形区域进行提取和恢复,但提取的模糊区域并不准确,所以在前景和背景融合后有分层现象,并且在运动模糊估计算法时间太久,实时性不强。因此,目前去模糊方法难以较好地复原复杂运动模糊图像。

本文针对复杂的车载模糊图像进行研究。车载图像的背景区域包含全局运动模糊,而局部运动区域包含了2种运动模糊,借鉴上述再模糊理论与分区域复原的思想,提出一种复杂车载运动模糊图像的复原方法。具体为:采用改进的模糊核估算方法,估算出图像的全局运动模糊参数,对图像进行全局运动模糊复原,改进的算法能更好地估算模糊参数,精度更高、效率更快;基于再模糊理论的思想,根据去全局运动模糊前后的图像的结构相似度(Structural Similarity, SSIM)和局部均方差特点,检测和分割出局部模糊区域,比文献[8]提取的局部模糊区域更准确,合成不会出现过渡不自然;将复原后的模糊区域与背景区域拼接合成最终的清晰图像。

1 相关理论

1.1 再模糊理论

Crete等[9]提出的图像再模糊理论是对原待测图像进行再模糊处理,借助模糊前后2幅图像之间像素的差异以及变化来评价原始图像的模糊程度。一副清晰的图像,拥有突出的轮廓和细腻的纹理信息,经过模糊处理后会损失较多的细节信息,而再次对模糊的图像进行模糊处理,可损失的细节信息将大大减少。从空间域来看:模糊处理主要是减小了相邻像素之间的差异,使某一图像块中相邻像素的差异减小,再模糊对像素之间差异的影响远小于第一次模糊;而从频域来看:模糊处理主要是减少了图像块的高频部分,使得图像分布在中低频部分,再模糊则可减少高频部分不多。如图1(a)～图1(c)依次为清晰图像以及2次模糊图像,第一次模糊后损失大量细节信息,模糊前后图像差异大,再次模糊则损失细节较少。

图1 再模糊实验图及直方图Fig.1 Re-blur experiment diagram and histogram

图1(d)～图1(f)为原始图像以及再模糊处理后的灰度直方图。可以看出,原始图像的灰度差很大,且高频较多,经过再模糊处理后第二幅图像的高频减小,且灰度之间的差异变小,再到第三幅图像可以明显看出灰度差值不大,相邻的灰度值比较平均。因此可以通过对比模糊前后的图像的相关差异,来检测识别出局部模糊区域的位置。

1.2 图像局部均方差和SSIM

图像的局部均方差可较好地体现图像的细节信息,当图像模糊时,图像相邻间的像素关联性较强、变化缓慢,从而均方差变小。因此对于模糊失真的图像比较敏感,可用均方差来比较2幅图像是否模糊。图像的均方差是基于像素点来判断的,并未考虑人眼的视觉观感,所以时常出现评价的图像与人眼观感有差异,从而导致采用均方差判断的图像为模糊,但是实际人眼观察到的图像并不模糊。图像的SSIM是基于人眼视觉系统提出的一种图像评价模型,因此结合图像的局部均方差和SSIM来判断图像块是否模糊,能使判定结果更准确且符合人的主观感受。

图像的局部均方差能够反映图像块中像素的领域关系,且还可以表示图像块中像素灰度变化的剧烈程度。对于一副图像计算局部方差时,区域大小一般取(2k+1)(2k+1),其中k为正整数。图像的局部均方差如下:

(1)

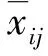
图像具有很高的结构性,主要表现为图像像素间存在强相关性,可以通过SSIM来衡量图像的质量。SSIM主要用在图像的质量评估等领域,从亮度、对比度和结构三方面来衡量图像的相似性[10-12]:

(2)

式中:μx、μy为灰度均值,σx、σy为灰度均方值,σxy为灰度协方差,C1、C2、C3为保证分母不为0的常数,l(x,y)、c(x,y)、s(x,y)分别为亮度、对比度和结构对比度计算,S(x,y)为SSIM。

2 基于再模糊理论的运动模糊检测与复原

运动模糊分为全局运动模糊和局部运动模糊。全局运动模糊是整幅图像只有一个模糊核,排除噪声的干扰,若已知模糊核和模糊图像则可复原图像;局部运动模糊图像中运动区域表现为模糊,而其他区域清晰,若采用相同模糊核对图像进行复原,虽然模糊区域会恢复清晰,但原本清晰区域会产生振铃效应,所以需要单独分割出模糊区域进行模糊复原,再与清晰的区域拼接融合,完成图像的复原。如果整幅图像既有全局运动又有局部运动,则对整幅图像的复原带来困难,本文先求出全局运动模糊核,对图像进行全局模糊恢复,去除全局运动模糊;再分割出局部模糊区域,对其进行复原;最后合成清晰的图像。算法流程如图2所示。

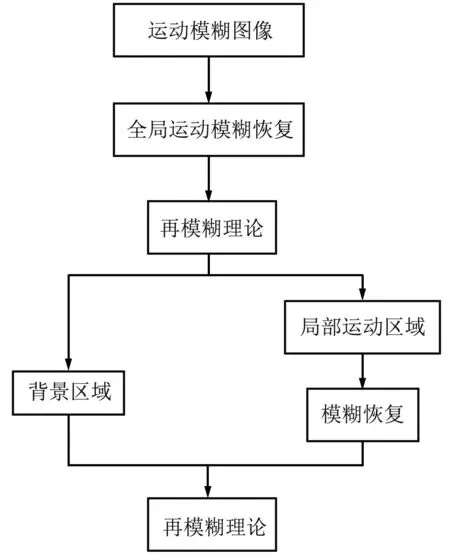
图2 算法流程Fig.2 Flowchart of algorithm

2.1 全局运动模糊的检测与复原

要求解出图像的全局运动模糊参数,就是对仅有全局模糊的图像块进行模糊核估计,利用该模糊核对图像进行全局运动模糊复原。图像的车身区域无运动的物体,也为背景的一部分,而图像背景部分具有统一的模糊参数,因此本文通过车身区域的模糊块来计算出图像的全局运动模糊核,排除局部运动的干扰。首先对图像进行高斯低通滤波去除部分噪声的影响,然后求出全局运动模糊核对图像进行复原,得到清晰背景图像。

(1)图像模糊退化原理

相机运动生成模糊图像,可表示为:

g(x,y)=f(x,y)*h(x,y)+n(x,y),

(3)

式中:*为卷积运算,g(x,y)为模糊的图像,f(x,y)为理想清晰图像,h(x,y)为退化函数,即点扩散函数(PSF);n(x,y)为噪声。将上式通过傅里叶变换后,转化为频率域,得到:

G(u,v)=H(u,v)F(u,v)+N(u,v),

(4)

式中:G(u,v) 、H(u,v) 、F(u,v)、N(u,v)分别为g(x,y)、f(x,y)、h(x,y)、n(x,y)的傅里叶变换结果。可以看出,若要复原模糊图像,模糊核和噪声是影响复原效果的主要因素,而噪声与H(u,v)的大小有关,当H(u,v)足够小时,噪声是影响图像质量的主要因素,在复原过程中,部分噪声被当作图像的高频造成图像模糊[13]。

若已知模糊图像以及退化函数,忽略噪声的影响,则进行去卷积操作得到原始的清晰图像,而PSF可用式(5)表示:

(5)

式中:θ为运动模糊角度,l为运动模糊尺度。

若已知模糊角度和运动模糊的尺度就可得到模糊核,在模糊图像块的频谱图中,亮暗条纹相间,可通过相间条纹的角度来计算出模糊角度,一般使用Radon变换来估算出方向。模糊图像的像素点具有很强的相关性,像素点的灰度值逐渐变化,因此可通过模糊图像的自相关函数图求得模糊尺度。但是由于外界因素的影响以及图像本身的特点,对图像进行傅里叶变换得到的频谱图会出现大量的毛刺和噪声,还有频谱图中心的十字亮线,因此现有的PSF估计方法还有一些不足[14]:频谱图中的十字亮线会影响条纹间的距离以及方向,导致Radon变换后估算出的模糊方向存在一定的偏差;频谱图中的噪声也会影响亮条纹的检测。若模糊长度较小,则条纹间距过大、数量较少,噪声在条纹中间占比大,没有足够的明显条纹信息支撑Radon变换,直接去除噪声则会导致图像估计有偏差。

(2)改进的PSF估计算法

综上所述,本文提出一种改进的运动模糊估计方法,具体步骤如下:

① 获得模糊图像的频谱图。图3为运动模糊图像,对运动模糊图像取车身图像块进行傅里叶变换,把得到的频谱图进行动态范围的压缩居中,如图4所示。图5为直接进行边缘检测图。

图3 运动模糊图像Fig.3 Motion blur image

图4 频谱图Fig.4 Spectrogram

图5 直接边缘检测图Fig.5 Direct edge detection diagram

② 把频谱图进行形态学运算。把步骤①中的频谱图进行膨胀腐蚀操作,如图6所示,可以看出腐蚀操作去除了亮条纹中的噪声点,与原频谱图相比,亮条纹更明显,因此也降低了频谱图中的十字亮线的影响。

图6 处理后频谱图Fig.6 Spectrogram after processing

③ 运动模糊长度的估计。把步骤②中的频谱图进行二值化操作,使得亮暗条纹更明显且冗余信息少。对二值化后的图像进行边缘检测,然后对边缘检测图进行膨胀腐蚀操作,如图7所示,从图中可以看出几乎没出现十字亮线对边缘检测产生影响。采用Canny算子对边缘图像进行以及微分以及自相关计算,通过自相关图像计算出模糊长度,如图8所示。

图7 边缘检测图Fig.7 Edge detection graph

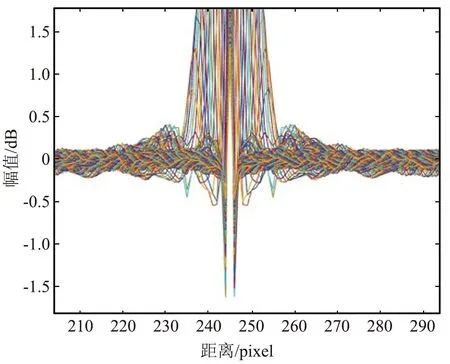
图8 自相关图Fig.8 Autocorrelation diagram

④ 运动模糊角度的估计。对步骤③中的边缘检测图像进行Radon变换,通过变换图估算出模糊方向,Radon变换如图9所示。

图9 Radon变换Fig.9 Radon transformation

(3)盲复原算法对比分析

噪声和模糊核的准确性是运动模糊图像复原的关键。因此,为进一步验证噪声对运动模糊图像的复原影响以及几种算法的复原效果,采用几种典型的复原算法对模糊图像进行复原。图10和图11为维纳滤波、最小二乘方滤波法以及Lucy-Richardson(L-R)滤波对图像进行复原。第一组实验结果图10为无噪声的图像复原实验图,第二组实验图11为含噪声的模糊图像复原结果。依次为原始图、运动模糊图、维纳滤波复原图、最小二乘方复原图和L-R滤波算法复原图。

图10 无噪声实验对比Fig.10 Comparison of noise-free experiments

图11 含噪声实验对比Fig.11 Comparison of experiments with noise

从无噪声实验的对比图10可以看出,L-R算法的复原效果与迭代次数有关,迭代次数为25时复原效果最好,但产生了明显的振铃效应,图像边缘出现重影;而选取最佳K值的维纳滤波以及最小二乘方复原效果比较理想。

从含噪声的实验对比图11可以看出,迭代次数为30时为最佳选择,L-R算法对噪声有一定的抑制,但复原效果不理想;最小二乘方滤波法复原效果理想,但对噪声抑制作用小;最佳K值的维纳滤波复原效果最好,图像中的噪点明显减少,图像细节信息基本恢复。综上实验结果对比分析,采用维纳滤波算法复原图像。

2.2 局部运动模糊的检测

本文根据再模糊理论的思想,把全局运动模糊复原前的图像视作再模糊后图像,复原后的图像视作模糊前的图像,节省了对图像再模糊的过程,节省了大量的时间。由于运动的物体在非车身区域,因此基于再模糊理论针对非车身区域进行局部运动模糊检测,可以减少处理区域、节省时间。算法步骤如下:

① 把全局模糊复原前后图像的非车身区域分为n×m块,计算每一小块区域的SSIM和局部均方差。对图像分块处理会减小运算量,极大缩短了算法时间,提高算法的实时性。

② 通过图像块模糊前后的局部均差来标记图像的模糊块和清晰块。图像块经过模糊后局部均方差会减小,通过把模糊前后的图像块局部均方差相减,若差值较大,则说明图像的变化大,标记为清晰块,相反则标记为模糊块;通过图像块模糊前后的SSIM来标记图像的模糊块和清晰块。对模糊前后图像块的SSIM作差,若差值较大,则说明图像的变化大,标记为清晰块,相反则标记为模糊块。

③ 对步骤②中的模糊块集合求交集,即为所求的模糊块。

④ 形态学处理。本文基于图像块来提取出模糊区域,因此存在边缘不平滑、不精准的问题,在拼接融合过程中会出现边缘过渡不自然;整个模糊区域中部分图像块被误判为清晰块,导致模糊区域中出现连接断续,不利于模糊区域的整体分割。所以需要对图像进行形态学中的先膨胀后腐蚀处理,精准标记出模糊区域。图12为模糊区域检测图,从左往右依次为模糊区域粗提取、模糊区域分割和分割后的模糊区域。

图12 模糊区域检测Fig.12 Blurred area detection

2.3 局部运动模糊的恢复及融合

采用算法对局部运动模糊复原后,需要和全局运动模糊复原图进行拼接融合,得到清晰的图像。图像融合是根据2幅图像中已经配准的特征点,将2幅图像拼接融合为1副图像,2幅图像拼接的交界处会存在不自然的过渡拼接缝,或者出现模糊重影,这是拼接融合的难点。由于线性融合流程简单,且效果好,本文选用加权平均融合的算法[15]。

图13为复原后的局部图像块与未复原的模糊图的配准,可以看出配准效果较好,不存在误匹配的特征点。配准的图像进行融合,图14为融合后结果,从图中可以看出,只有图中车辆边缘存在少许融合后边缘痕迹,对人眼观察无影响,因此融合效果较好。

图13 局部复原图像配准Fig.13 Partial restoration image registration

图14 清晰图像融合Fig.14 Clear image blending

3 实验结果与分析

为了验证本文算法的有效性,本文采用模糊图像进行对比实验。

(1)模糊参数估计实验对比

为验证本文参数估计方法的有效性,采用文献[3,16-17]以及本文算法进行对比,以图10(a)为标准测试图像,对图像进行模糊处理,将模糊长度设置为5、15 pixel,将模糊角度在0°～180°取值,步长为35,表1为模糊角度估计实验结果,表2为模糊长度估计实验结果。

表1 模糊角度估计结果

表2 模糊尺度估计结果

由表1可知,文献[3,16-17]估算的运动模糊角度平均误差为1.0°、1.5°、1.9°,本文估算的运动模糊角度平均误差为0.6°,最大误差为1.7°;由表2可知,文献[3,16-17]估算的运动模糊长度平均误差为1.1、0.9、1.4,本文估算的运动模糊长度平均误差为0.7 pixel,最大误差为2 pixel,本文估算的运动模糊长度和角度平均误差均小于其他方法,且最大误差较小。综上,本文方法具有更高的精度和鲁棒性。

(2)全局运动模糊复原实验

图15～图17为仿真结果,其中图(a)为实拍原始模糊图,图(b)～图(d)依次为文献[16]、文献[3]、文献[17]以及本文算法对图像进行模糊复原。为便于观察,将局部区域图像块放大后置于原图像下半部分。

图15 运动模糊实验1Fig.15 Motion blur experiment 1

从图15可以看出,几种算法对运动模糊复原都有不错效果,文献[16]算法细节处理较为平滑,但没完全复原图像中的模糊;文献[3]算法在交通标志和树叶的边缘位置有振铃效应;文献[17]算法对细节处理较好,但存在一定噪声;本文算法不仅清晰无振铃效应,且过滤平滑更符合人眼的视觉效应。在图16中,文献[16]算法和文献[3]算法在图像中边缘有明显的振铃效应;文献[17]算法增强了噪声,本文算法效果明显。在图17中,文献[3,16-17]的算法虽然复原效果不错,但存在振铃效应。综上,本文算法在车载模糊图像上复原效果较好。

图16 运动模糊实验2Fig.16 Motion blur experiment 2

图17 运动模糊实验3Fig.17 Motion blur experiment 3

评价图像的质量不仅有以上所述的主观评价,还有用参数来体现图像质量的客观评价。客观评价采用一种评价标准来评价图像质量好坏,常用的客观评价方法有峰值信噪比(Peak Signal to Noise Ratio, PSNR)和SSIM。PSNR反映了处理后的图像与原始图像失真程度,值越大算法复原效果越好。但有时采用PSNR评价的结果与人眼观感不符,所以采用PSNR和SSIM来评价图像的质量[18-19]。表3为几种算法实验对比图对应的PSNR和SSIM值,表4为算法运行时间对比。

表3 对比实验结果

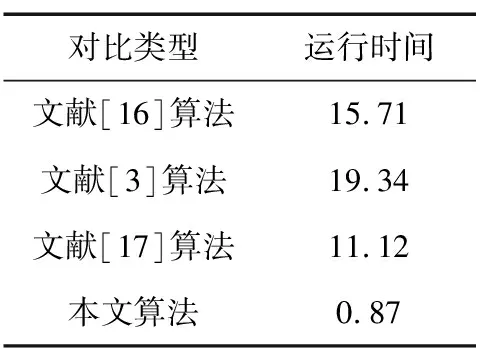
表4 算法时间对比

由表3可知,本文算法的PSNR和SSIM平均最高,表明在客观评价上,本文算法复原效果最好,复原后的图像质量最高。由表4可以看出,本文算法效率比其他3个文献的效率更高,算法运算时间为0.87 s。算法运算时间与估计的模糊区域范围大小有关,本文是取整幅图像的一小块来进行模糊估计,极大缩短了算法时间。

(3)混合运动模糊复原实验

图18～图20为实测的混合运动模糊车载图像实验图,其中实验1和实验2为局部运动模糊为行驶车辆,实验3的局部运动模糊为行人,3组实验具有代表性。图(a)为原始的混合模糊图像,图(b)为去除全局运动模糊后的图像,图(c)为局部运动和全局运动模糊复原后的清晰图像。为便于观察,截取图中局部模糊和全局模糊部分图像放大,置于原图下方。

图18 混合运动模糊实验1Fig.18 Mixed motion blur experiment 1

在图18及图19中,由图(b)可以看出,行驶的车辆区域比图(a)中的更加清晰,而背景部分几乎得到复原,无明显的振铃效应和噪声,图(c)中行驶的车辆基本得到复原,除边缘有少许融合痕迹,整幅图像较为清晰;在图20(b)中的全局复原后的区域为车身,复原效果较好且无振铃效应,虽然图20中的局部模糊范围小,但从图(c)中可以看出行人部分复原效果不错。

图20 混合运动模糊实验3Fig.20 Mixed motion blur experiment 3

表3为以上3组运动模糊复原实验对应图像的PSNR和SSIM值,表5中(a)～(c)分别为原始混合模糊、去全局运动模糊以及去局部运动模糊图。可以看出3组实验的原始混合运动模糊图(a)的PSNR和SSIM都较低,经过全局运动模糊复原后的图(b)和图(a)相比,PSNR以及SSIM平均提高了15.2%、19.6%。经过局部模糊复原后,SSIM和PSNR也有一定提升。综上对比分析可知,本文算法对混合运动模糊的车载图像复原有不错的效果。

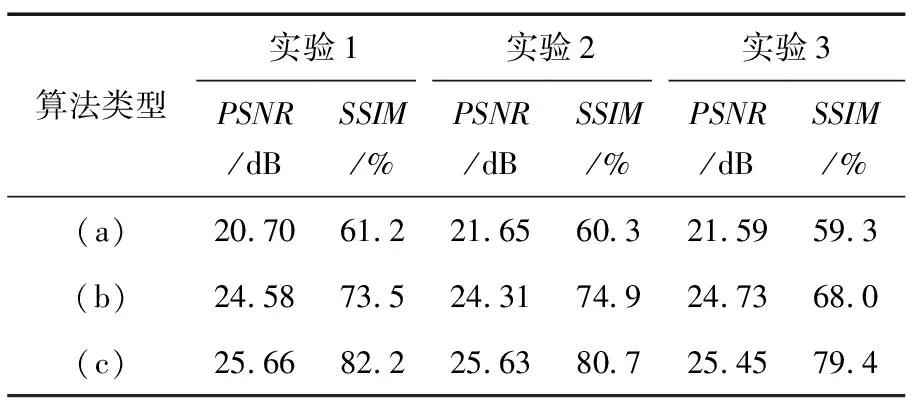
表5 模糊复原实验结果

(4)混合运动模糊复原实验对比

采用本文算法与文献[8]算法进行对比,图21(a)～图21(c)分别为原始模糊车载图像、文献[8]算法实验以及本文实验结果。可以看出,文献[8]算法对局部和全局采用2种恢复算法存在差异,调整亮度后仍然存在分层现象,且局部运动的矩形区域复原后存在边缘融合痕迹,提取的局部区域不准确,而本文算法复原后无明显痕迹,效果好。在背景区域本文算法复原无明显振铃现象,文献[8]边缘存在振铃现象。

图21 混合运动模糊实验对比Fig.21 Comparison of mixed motion blur experiment

4 结束语

本文对复杂的车载模糊图像进行研究,提出一种基于再模糊理论的复杂车载模糊图像复原方法。对PSF估计算法改进和优化,对车身区域估算出全局模糊参数,利用该参数对图像进行全局模糊复原,充分利用了模糊图像的特点;基于再模糊理论的思想,通过全局模糊复原前后的图像提取出局部运动区域,节省了再模糊的时间,提高了算法的时效性;对局部运动区域复原后与背景区域融合,完成整幅图像的复原。实验证明,本文算法复原的图像PSNR和SSIM值都得到了提升。本文算法的复原效果较好,且适用于复杂的车载模糊图像,具有一定的应用价值。