铁路枢纽双编组站静态配流协同优化研究

户佐安，朱 雨，怡智航，陈 将

(1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.西南交通大学 综合交通大数据应用技术国家工程实验室，四川 成都 611756；3.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；4.中国铁路成都局集团有限公司 遂宁车务段，四川 遂宁 629000)

0 引言

编组站是铁路运输重要的基层生产单位，优化编组站配流方案对加速车辆周转、提高运输能力具有重要意义。我国部分铁路枢纽拥有2 个及以上编组站，并且存在枢纽内资源利用不合理的情况，为优化枢纽内运输组织的整体水平，达到全局最优，整体考虑枢纽内2 个编组站的车流，进行铁路枢纽双编组站静态配流协同优化研究，这对于促进枢纽内车辆周转，提升铁路枢纽运输能力具有较强的现实意义。目前国内外学者针对编组站配流相关问题已展开不少研究。Haahr 等[1]构建混合整数规划模型，对分类线运用子问题设计贪婪启发式算法进行求解；Gestrelius等[2]综合考虑到发线运用及解体方案，构建整数规划模型进行求解。Jing 等[3]将编组站的技术作业过程描述为流水作业过程，建立静态配流网络模型并采用禁忌搜索算法求解。马亮等分别构建了静态配流字典序多目标积累调度模型[4]和动态配流分层模型[5]。赵金观等[6]以正点出发列车数最多为目标，建立广义动态配流问题模型；唐金金等[7]以全服务网络总旅行费用最小为目标，建立服务网络动态配流优化模型；郭瑞等[8]研究多阶段优化方法的调度策略及启发式规则，设计多阶段分层启发式配流算法求解；薛锋等[9]将编组站资源可用度引入编组站配流模型，利用分层优化方法求解；李晟东等[10]着眼于提高运输时效性，将货物运到期限引入配流优化模型，并采用模拟退火算法求解；许可等[11]建立基于车流接续代价最小的编组站配流优化模型并设计相应算法求解。于婕等[12]以优先级加权的货物总在站停留时间最小和发出总车辆数最多为双目标建立动态配流优化模型。上述文献均基于单编组站为研究主体进行配流优化，未考虑跨编组站车流的协同性，仅有陈磊[13]提出构建基于编组站综合自动化系统(CIPS)的跨站协同运输计划编制平台；武旭等[14]以两技术站正点出发列车数最多为目标，构建技术站间货物列车协同配流模型。

综上所述，部分文献考虑了车辆在站停留时间作为优化目标，但忽略了出发列车的等级高低及车流分配优先性。且大部分文献在进行配流的协同优化时以车站内部作业之间的协同为主，忽略了编组站间车流分配的协同。在已有研究的基础上，从枢纽内编组站间协同配流的角度出发，研究铁路枢纽双编组站静态配流协同优化问题，为编组站配流问题的优化提供一定的参考。

1 问题描述

双编组站静态配流协同优化问题可描述为：中转车流随部分改编中转列车或到达解体列车陆续到达枢纽内两编组站，当制定某一编组站的配流方案时，全局考虑两编组站的到达车流。枢纽内车站分布示意图如图1所示，若P站某一去向(如f去向)到达车流不足致使列车无法正点满轴开行时，将Q站f 去向的符合接续时间要求的车流编入小运转列车送至P站，参与编组，保证列车满轴且正点开行。

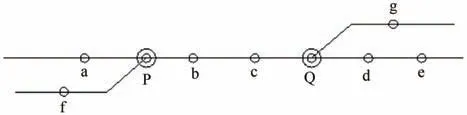
图1 枢纽内车站分布示意图Fig.1 Station distribution within the hub

2 模型构建

2.1 模型假设

（1）枢纽内2个编组站分工方案既定。

（2）枢纽内两编组站采用单推单溜作业方式，两编组站分别由一台调车机车负责解体作业、一台调车机车负责编组作业。

（3）列车按照到达计划到达车站，不考虑波动性。

（4）车站接发车能力及容车能力充足，线路区间通过能力充足。

（5）列车解编顺序采取先到先解、先发先编原则。

2.2 目标函数

目标函数1 为双编组站配流总代价最小，目标函数2为双编组站的总满轴列车数最多。

式中：Z1表示双编组站配流总代价；Z2表示双编组站 总 满 轴 列 车 数；i(i= 0，1，2，...，m) 与i'(i'=0，1，2，...，m')分别为P 站和Q 站到达列车索引，i= 0 与i'= 0 分别表示本阶段开始时P 站与Q 站的站存车，m与m'分别表示P 站与Q 站的到达列车索 引 最 大 值；j(j= 1，2，...，n，n+ 1) 与j'(j'=1，2，...，n'，n'+ 1)分别为P 站和Q 站出发列车索引，j=n+ 1 与j'=n'+ 1 分别表示本阶段结束时P 站与Q 站未被编组的站存车；k(k= 1，2，...，p)为去向索引，p表示去向索引最大值；ci，k，j为到达列车i中k去向车组为出发列车j供应车流的代价，ci'，k，j，ci，k，j'和ci'，k，j'同理；xi，k，j表示到达列车i中去向为k的车组为本站出发列车j提供的车流量，xi'，k，j，xi，k，j'和xi'，k，j'同理；yj表示出发列车j是否满轴，yj'同理，若满轴，其值为1，否则为0。

其中，配流代价的确定方法参考文献[15]，若列车违编或到达列车与出发列车的接续时间超过了最小接续时间限制，其配流代价视为一充分大正数。其余出发列车按其等级以直达、直通、区段、摘挂、小运转的顺序排列，对等级相同的列车，按其编组去向数升序排列，对等级和编组去向数均相同的列车按其出发时刻由早到晚排列。以序号作为配流代价，具体计算公式见公式—。

2.3 约束条件

（1）车流量约束。

式 中：li，k表 示 到 达 列 车i中k去 向 的 车 数，li'，k同理。

公式⑶和⑷表示枢纽内两编组站的到达列车中k去向的车辆数之和等于出发列车和阶段结束时站存车中k去向的车辆数之和。

（2）车流接续时间约束。

式中：T为到达列车i的解体作业最早开始时刻，同理；表示到达列车i的到达时刻，其中T为本阶段开始时刻，T同理；TDJ为到达列车的技术作业时长；T为出发列车j的最晚编组作业开始时刻，T同理；T表示出发列车j的出发时刻，其中T和T为本阶段结束时刻，Tcfj'同理；TcJ为出发列车技术作业时间；TB为两编组站的编组作业时长；gi，j表示到达列车i的解体完毕时刻是否早于出发列车j的编组开始时刻前，若是，其值为1，否则为0，gi'，j，gi，j'和gi'，j'同理；M是一充分大的正整数；T为到达列车i的解体作业开始时刻，T同理；TJ为两编组站的解体作业时长；T，T，T，T分别为小运转列车的编组作业时长、出发技术作业时长、到达技术作业时长及解体作业时长；tpq表示列车从P至Q的运行时间，tqp同理。

公式⑸和⑹表示各编组站内到达列车的最早解体时刻；公式⑺和⑻表示各编组站内出发列车的最晚编组时刻；公式⑼—⑿表示车流正点接续约束；公式⒀—⒃表示到达列车与出发列车之间的接续时间约束。

（3）不违编约束。

式中：fk，j表示出发列车j的编组去向是否包括去向k，fk，j'同理，若包括，其值为1，否则为0；hi，k代表到达列车i编组去向是否包括去向k，hi'，k同理，若包括，其值为1，否则为0。

公式⒄—⒇表示出发列车编组内容约束，即各编组站的出发列车配入的车流，其去向必须在编组计划的规定内；公式—表示到达列车编组内容约束，即只有去向在编组计划内的车流才可编入该出发列车。

（4）配流代价约束。

式中：wj和wj'为出发列车排序序号。

（5）出发列车满轴要求约束。

式中：Lj和Lj'表示出发列车满轴车数；qj和qj'表示出发列车的质量或长度要求，若必须满轴则取值为1，否则取值为0。

（6）满轴判断约束。

（7）调机资源约束。

式中：T为出发列车j的编组作业开始时刻。

（8）逻辑约束。

3 模型求解

双编组站静态配流协同优化问题需要同时对配流代价和满轴列车数进行优化，并且变量及约束条件较多，为确保在一定时间内求得较优方案，提升求解效率，采用理想点法进行求解，首先分别以两目标函数构造单目标优化模型，求得理想值，然后以两个优化目标与各自理想值的距离和最小为新的目标函数，将多目标转化为单目标，具体步骤如下。

步骤1：将目标函数统一为求最小化，将maxZ2转化为，其 中Z3表 示 双编组站总满轴列车数。

步骤2：分别以模型中的2 个目标函数Z1和Z3为目标构造单目标规划，分别依次求出Z1min和Z3min，以其求出的最优值分别作为该目标的理想值。

步骤3：计算每个目标与理想值的距离，并无量纲化，得到以下评价函数，其中Z表示无量纲化后的目标函数值。

步骤4：以minZ作为新的优化目标，结合模型约束条件再次求解，所求结果为将2 个优化目标综合考虑求解的最优值，故此最优解为原多目标规划的有效解，即问题的满意解。

4 算例分析

4.1 算例条件

某枢纽内含2 个编组站P 和Q，两编组站作业分工既定。编组站P 和Q 均配备解体调机1 台和编组调机1 台，采用单推单溜驼峰作业方案。列车编成辆数取35 辆。到达列车技术作业时长与出发列车技术作业时长均为30 min，解体作业时长均为15 min，摘挂列车与小运转列车的编组作业时长为20 min，直达列车、直通列车、区段列车的编组作业时长为15 min。取测试到达阶段时段为9：00—13：00，站存车信息表如表1所示。

表1 站存车信息表 辆Tab.1 Local wagon data

到达列车车流信息表如表2所示，其中43002，41003，45002，46001为摘挂列车。

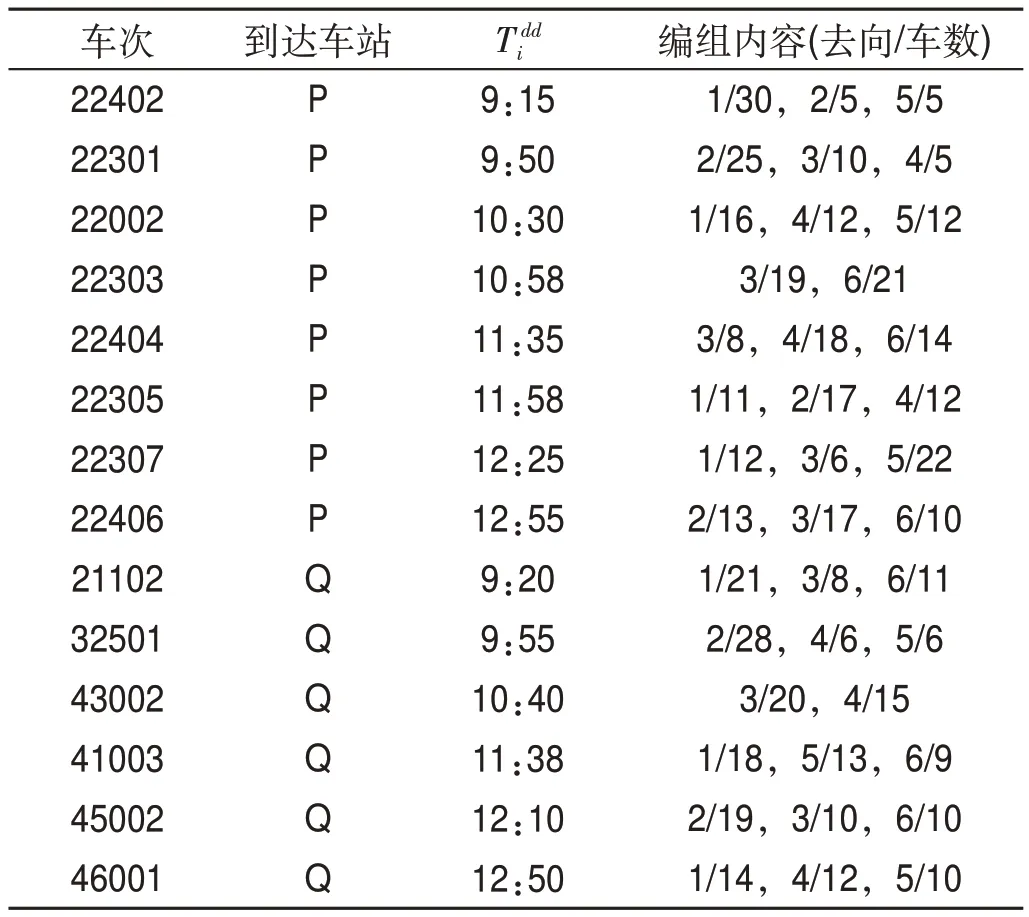
表2 到达列车车流信息表Tab.2 Wagon flow information of arrival trains

取测试出发阶段时段为11：00—15：00，出发列车车流信息表如表3 所示，其中43101，45202，43001，41004，45001，46002为摘挂列车。

表3 出发列车车流信息表Tab.3 Wagon flow information of departure trains

4.2 算例求解

按照“先到先解、先发先编”的顺序来确定列车的解编顺序，即静态配流，由此推算出编组站P到达列车解体作业信息表如表4 所示，编组站Q 到达列车解体作业信息表如表5 所示。编组站P 出发列车编组作业信息表如表6 所示，编组站Q 出发列车编组作业信息表如表7所示。

表4 编组站P到达列车解体作业信息表Tab.4 Break-up information of arrival trains at marshalling station P

表5 编组站Q到达列车解体作业信息表Tab.5 Break-up information of arrival trains at marshalling station Q

表6 编组站P出发列车编组作业信息表Tab.6 Marshalling information of departure trains at marshalling station P

表7 编组站Q出发列车编组作业信息表Tab.7 Marshalling information of departure trains at marshalling station Q

依照列车等级、编组内容和出发时刻，编组站P 出发列车等级排序如表8 所示，编组站Q 出发列车等级排序如表9所示。

表8 编组站P出发列车等级排序Tab.8 Class of departure trains at marshalling station P

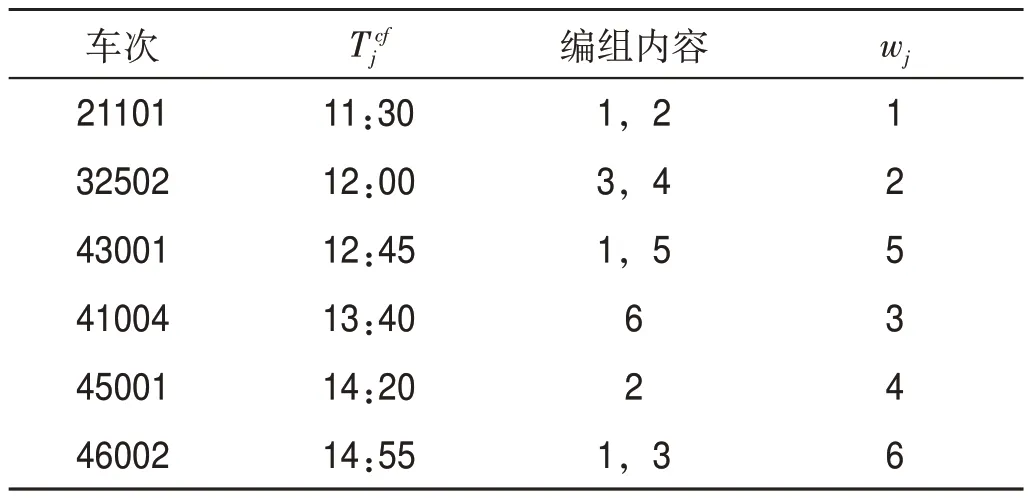
表9 编组站Q出发列车等级排序Tab.9 Class of departure trains at marshalling station Q

基于算例数据以及第3 节中的模型求解算法，运用数学软件对算例进行求解，求得Z1min=2 261 560，Z3min=-12，通过理想点算法求得编组站P配流方案如表10所示，编组站Q配流方案如表11所示，编组站P 阶段结束时站存车情况如表12 所示，编组站Q 阶段结束时站存车情况如表13所示。

表10 编组站P配流方案Tab.10 Wagon-flow allocation scheme of marshalling station P

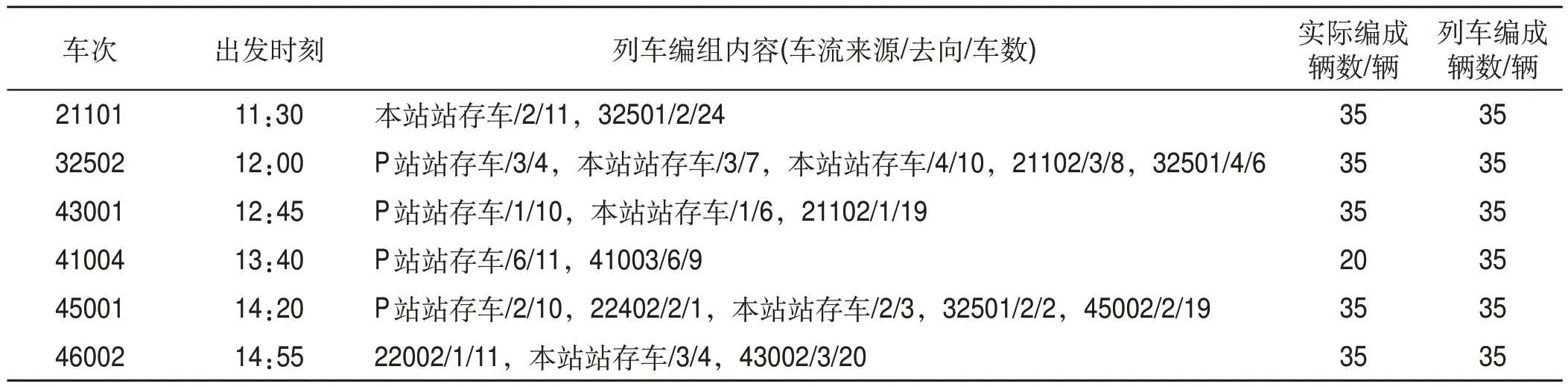
表11 编组站Q配流方案Tab.11 Wagon-flow allocation scheme of marshalling station Q

表12 编组站P阶段结束时站存车情况Tab.12 Remained local cars at marshalling station P

表13 编组站Q阶段结束时站存车情况Tab.13 Remained local cars at marshalling station Q

为检验该模型的优化效果，求出各编组站分别配流的结果，对比双编组站联合配流及各编组站分别配流，配流效果对比如表14所示。

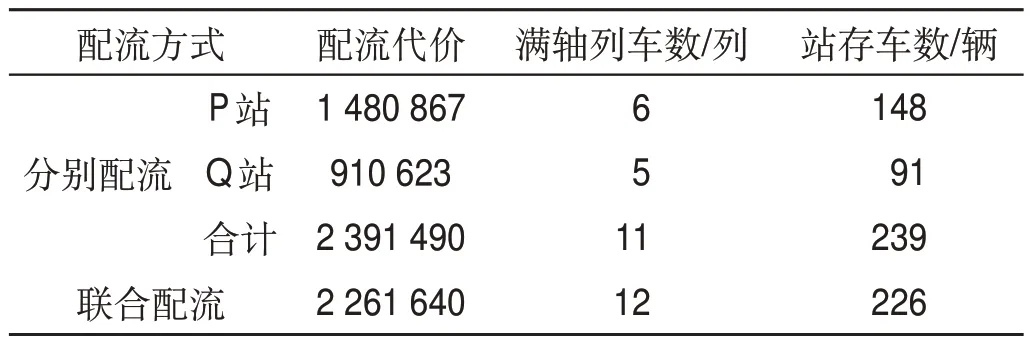
表14 配流效果对比Tab.14 Contrast of wagon-flow allocation effect

将对比结果进一步整理分析，出发列车满轴率对比图如图2所示。

图2 出发列车满轴率对比图Fig.2 Contrast of full-axle rate for departure trains

模型与求解方法可快速求得双编组站协同配流方案，与人工编制计划相比，可大幅节约时间、减少劳动强度。由表10—表13 可得，出发列车中除摘挂列车43101，41004 外，均满轴出发。由表14可知，联合配流的配流代价为2 261 640，分别配流的配流代价总和为2 391 490，降低5.4%；联合配流满轴列车数为12列，分别配流的满轴列车数总和为11列，提升9.1%；联合配流站存车数为226辆，分别配流的站存车数总和为239辆，降低5.4%，具有较好的优化效果。根据图2，联合配流时，编组站P 与编组站Q 的出发列车满轴率分别为87.5%和83.3%，两站平均出发列车满轴率为85.7%大于两编组站分别独立配流的总满轴率78.6%。

研究结果表明，针对拥有多编组站的铁路枢纽，联合配流可提升满轴率，保证更多的列车正点满轴。提出的模型及算法能在铁路枢纽全局角度，进行跨编组站协同静态配流，可为铁路枢纽整体运输组织水平的提升提供一定的参考价值。

5 结束语

从枢纽内双编组站配流协同优化的角度出发，考虑不违编约束、配流代价约束、车流接续约束等约束条件，建立铁路枢纽双编组站静态配流协同优化模型，并根据模型特点设计理想点算法求解，以此减少枢纽内两编组站的配流总代价及站存车总数，增加两编组站的总满轴列车数。最后通过算例及对比结果分析验证模型及算法的有效性，相比两编组站单独配流，两编组站联合配流的配流代价降低5.4%，站存车数减少13辆，满轴列车数增加1列，可有效提升枢纽内车辆周转率。当列车密集到发时，动态配流的引入，合理调整列车解编顺序有待进一步研究。