长距离地下综合管廊局部通风强化换热效果研究

尹海国 王烁焱 邓 鑫 康云飞

(西安建筑科技大学,西安)

0 引言

综合管廊已经在我国建设发展20多年[1],但仍然存在诸多问题,如管廊电缆舱内发热量超大,需要将热量排出以保证管廊内安全温度[2]。GB 50838—2015《城市综合管廊工程技术规范》[3]规定,当综合管廊内空气温度高于40 ℃或需进行线路检修时应开启排风机排风,并应满足综合管廊内的环境控制要求[4]。目前管廊内主要通过控制整体换气次数进行通风散热[5]。随着管廊长度的增加,为降低管廊后段高温区域的温度,管廊换气次数不断增大,导致管廊前段区域温度过低,造成能源浪费[6]。故而需研究更经济合理的管廊通风方式。

目前许多地下综合管廊工程将2个或3个防火分区作为1个通风单元[7],而防火分区中的防火门会强化管廊的通风换热效果,类似防火门的障碍物会增大通道断面速度,形成局部扰流而增强换热。朱金鹏通过模拟研究发现,管廊风速在防火门处会出现骤增现象,存在一个极值[8]。韦岩等人指出不同断面形状会影响电缆舱内的温度分布与散热效果[9]。Wang等人发现电缆舱内空气的阻塞作用生成的涡流降低了电缆的温度[10]。Meng等人也指出障碍物的存在会影响隧道临界通风速度[11]。基于这种特殊的现象,笔者提出了一种增强局部扰动的方法,即在管廊内安装射流风机,通过局部加速气流撞击管廊壁面来强化管廊内气流的局部扰动,达到增强换热的目的。射流风机在公路隧道中的成熟应用[12-13]在一定程度上印证了这种方法的可行性。

数值模拟是目前研究管廊通风散热的主要方法之一,在处理管廊内热烟气扩散问题上,林俊等人利用数值模拟分析软件得出了不同通风速度对管廊防火性能的影响[14]。叶爽等人利用CFD方法分析了不同管径管廊热力舱的最佳通风区,模拟结果与实验结果吻合度较好,误差为10%左右[15]。Wang等人基于数值模拟研究提出了新型活塞风通风策略,模拟结果和实验结果误差小于10%[16]。Li等人对管廊通风系统进行了实地测试,运用数值模拟方法对比了不同截面的风速分布,缩尺模型实验证实模拟误差在10%以内[17]。因此,本文研究也采用数值模拟方法建立管廊局部通风数值模型,从通风换热的角度研究管廊内设置射流风机的可行性。通过选取截面平均温度作为依据,分析管廊沿长度方向的通风换热效果。通过改变管廊进口风量和风机风量的比例,研究射流风机速度对管廊局部温度的影响。对比研究风机安装角度对管廊局部换热效率的影响,研究设定0°、45°、90° 3个安装角度。

1 数值模拟与实验验证

1.1 物理模型

本文研究基于目前地下管廊常用的施工方案,选取某采用盾构工艺敷设的电缆管廊为研究对象,管廊断面形状为圆形,管廊模型示意图见图1。管廊通风区间长度为200 m,管廊内存在6条电缆桁架,可以铺设4条3×110 kV电缆线路,电缆模型示意图见图2,管廊顶部布有弱电线路(10 kV),发热量小,计算时予以忽略。管廊两端的通风口简化为矩形风口(1 m×1 m),将每个桁架内的电缆线路简化为2条110 kV线路,共12条。在管廊顶部安装局部射流风机,风机直径D=0.35 m,管廊截面直径为10D=3.5 m。本文重点研究管廊内射流风机射流状态及其对管廊换热的影响,使用CFD方法建立了三维数值模拟模型,建模时对管廊内流动换热特性影响不大的细小结构进行了简化处理。

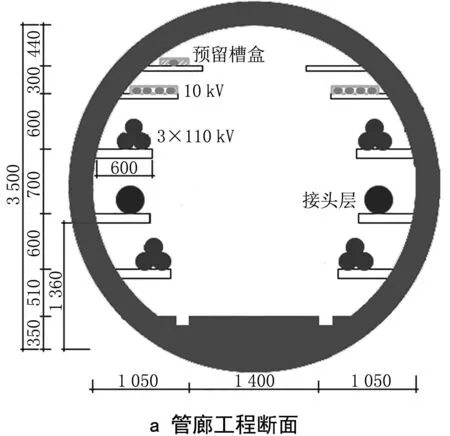
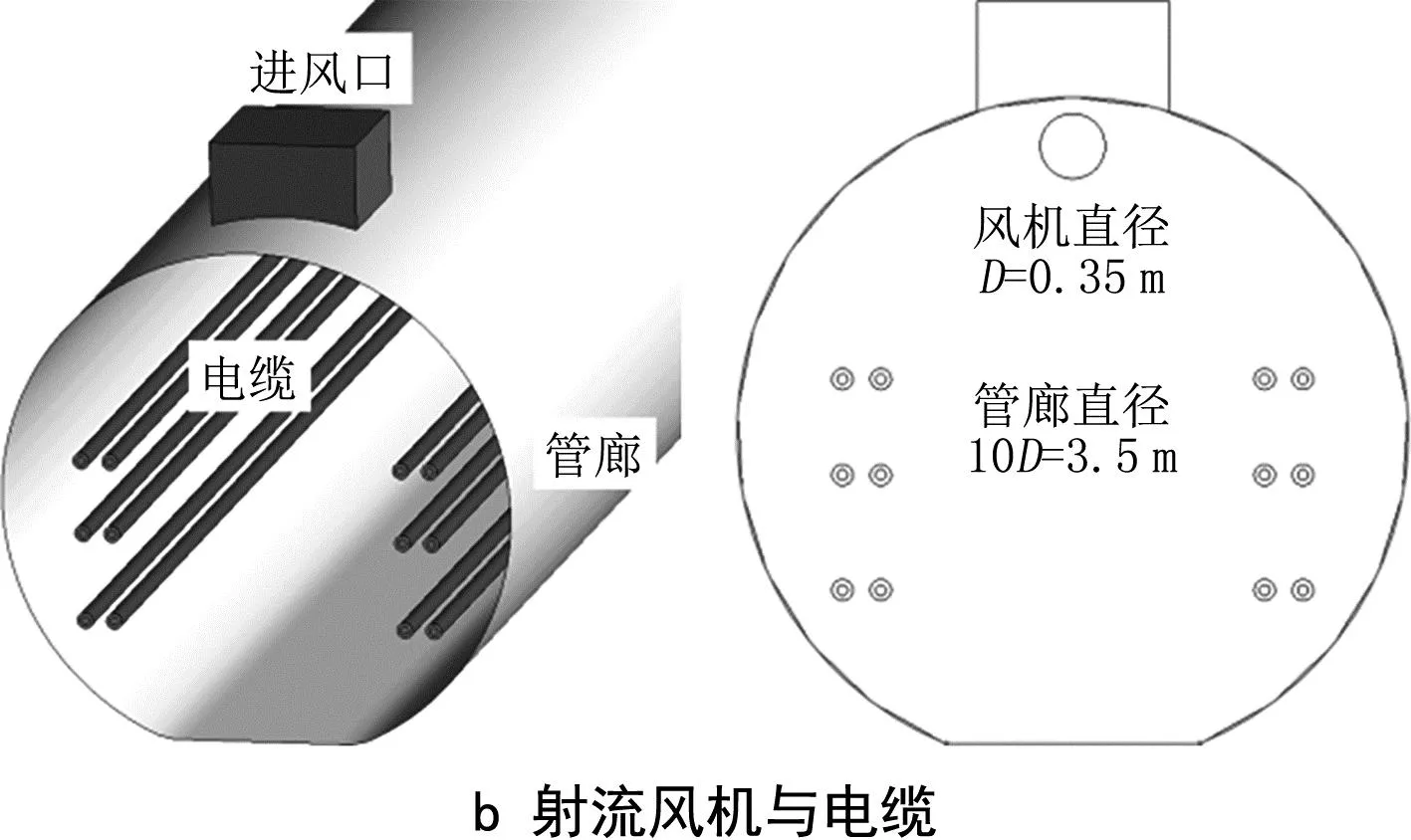
图1 管廊模型示意图

本文使用型号为64/110 kV的交联聚乙烯(XLPE)铝护套电缆,其剖面结构如图2b所示,电缆有多层结构,其中主要为保护层与导电体。将电缆外围各层简化为1个保护层,如图2c所示。

按照质量平均法计算简化后的电缆保护层的平均比热容：

(1)

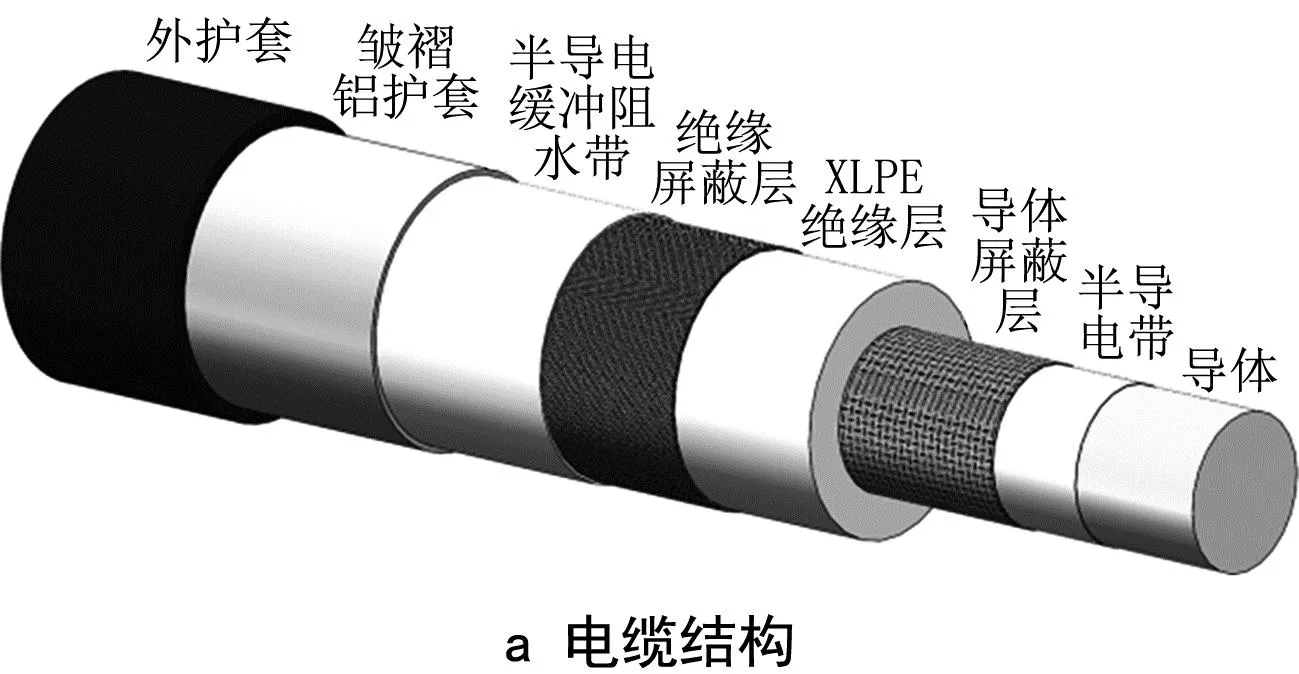
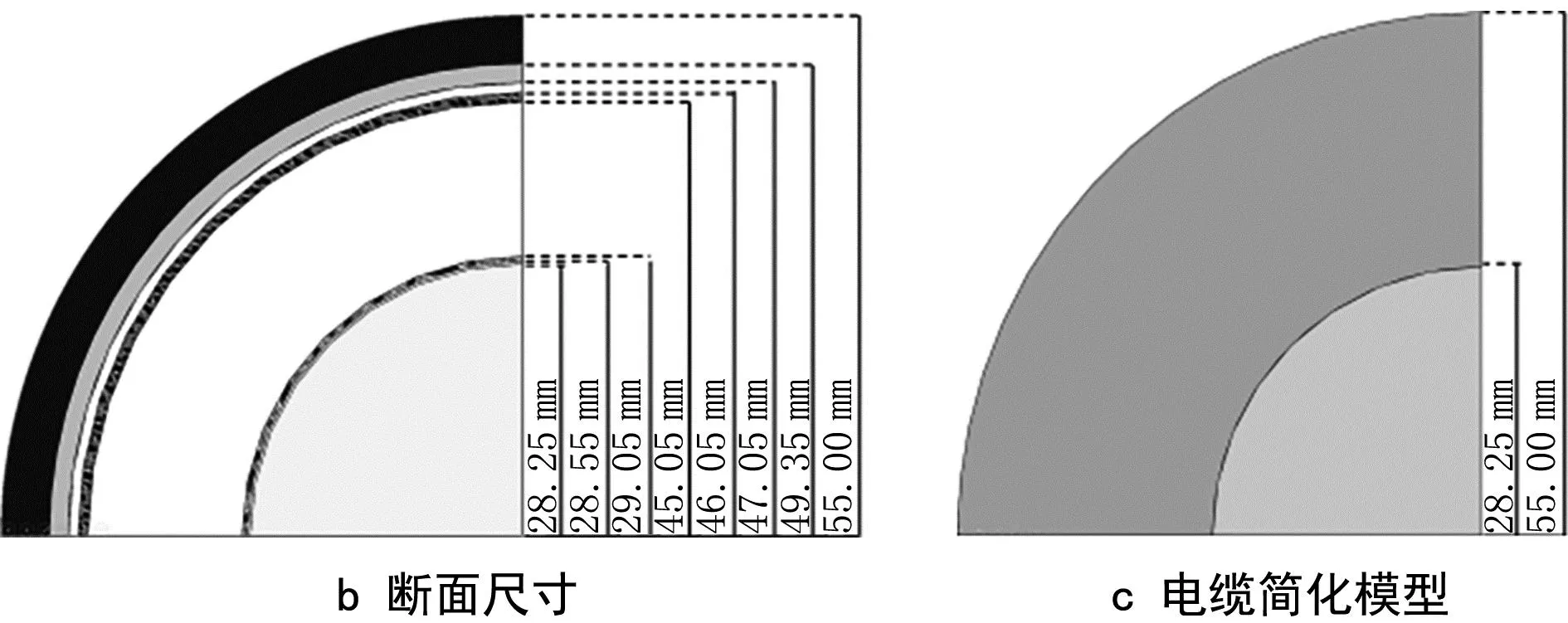
图2 管廊电缆模型示意图

式中ceq为平均比热容,J/(kg·K);n为电缆保护层材料层数;ωi为第i层材料质量分数;ci为第i层材料比热容,J/(kg·K)。

电缆保护层导热系数利用平均热阻计算：

(2)

式中λeq为平均导热系数,W/(m·K);ri为第i层半径,m;λi为第i层材料导热系数,W/(m·K)。

各层电缆物性及保护层相关参数见表1。

表1 110 kV电缆结构参数

使用商业软件ANSYS Fluent 19的SIMPLE算法进行求解计算。管廊内电缆发热量很大,在运行过程中空气被加热,在数值模拟时不能忽略温度对密度的影响,空气密度项使用Boussinesq假设。为了更好地计算湍流,选用RealizableK-ε模型,壁面函数使用Standard Wall Functions,Y+控制在30以上。采用结构化网格进行物理建模,如图3所示。计算收敛判断条件为湍流项残差值小于10-2,能量项残差值小于10-6。同时保证管廊进出口质量流量偏差在5%以内。

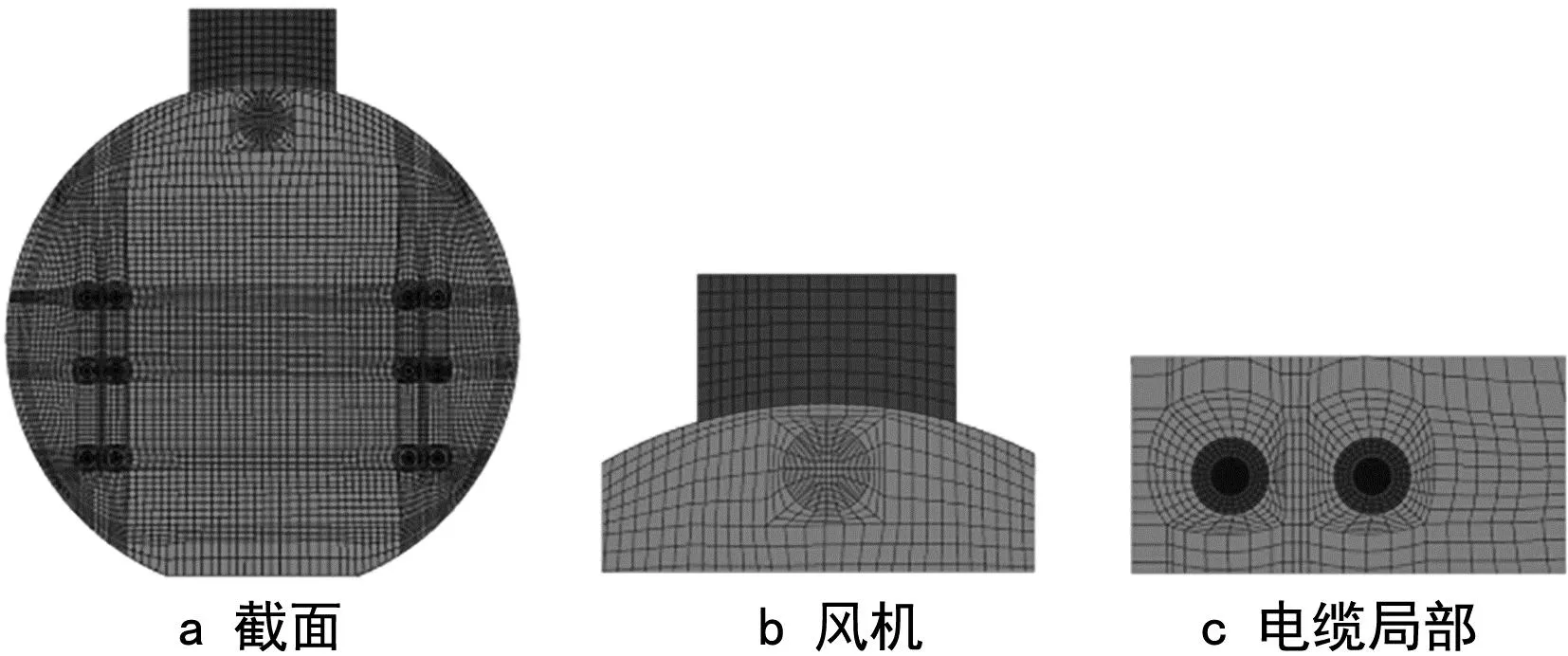
图3 管廊网格划分

1.2 数值模拟边界条件

本文所研究管廊使用的通风方式为机械排风+自然进风的组合方式。进风口为压力进口(pressure-inlet),相对压力为0 Pa。排风口处设置速度为负值的速度进口(velocity-inlet),进出口湍流项使用强度和水力直径(intensity and hydraulic diameter)定义,对于中等湍流强度,其强度值为5%,水力直径为1 m[18]。根据项目所在地室外气象参数,送风温度设为夏季室外计算温度(26 ℃)。为了确保管廊稳定运行,取土壤温度与室外计算温度相同。电缆表面为热源边界,电缆运行时产生的热量与电缆的载流量有关,计算式如下[19]：

(3)

式中Q为电缆热损失功率,W;b为电缆芯数量;k为功率系数,取0.6;L为电缆长度,m;σ为电阻率,Ω·mm2/m,取2×10-8Ω·mm2/m;I为负载电流,A;A电缆芯截面积,mm2。

本文研究的电缆发热采用体内热源,需要将管廊单位长度发热量转化为单位体积散热量,管廊电缆参数及计算散热量如表2所示。

表2 电缆参数及计算散热量

管廊壁面材料设定为混凝土,管廊中流体为普通空气,主要材料的物性参数如表3所示。

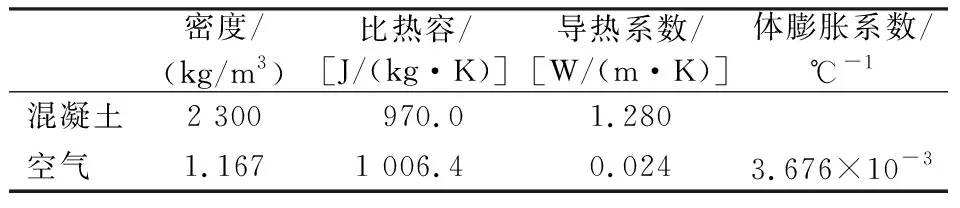
表3 主要材料物性参数

1.3 实验数据验证

为了验证数值模型的准确性,搭建1∶25缩尺模型实验台对射流风机后的风速衰减进行验证,如图4所示。圆形电缆舱缩尺模型直径为140 mm,长度为4 m,实验材料为透明亚克力板,风机为轴流风机,测试仪器为多功能气流测量仪(型号：SWEMA3000)与大风速探头(型号：SWA31),重点测量射流风机的速度衰减。沿风机轴线布置7个测点(前5个测点间隔0.05 m,后3个测点间隔0.20 m),如图4所示。实验与模拟结果的对比如图5所示。

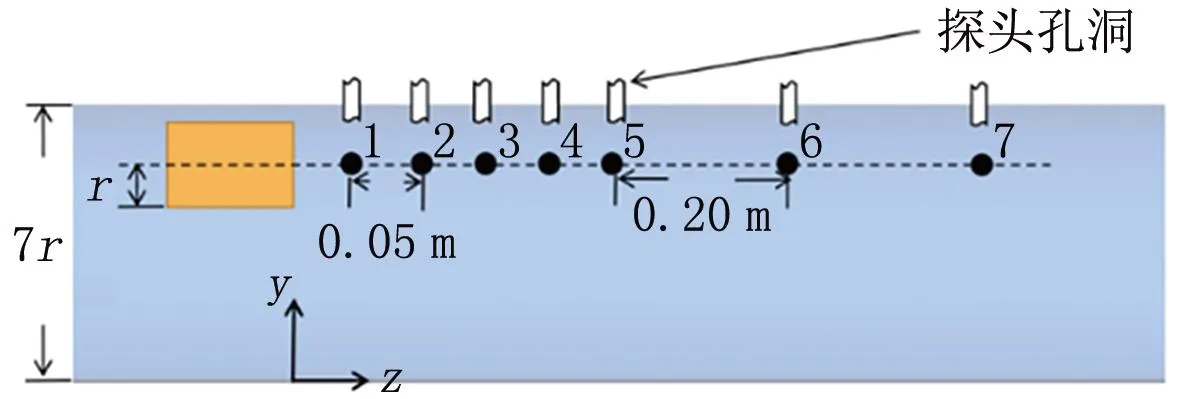
注：1～7为测点编号。图4 缩尺模型实验台布置示意图

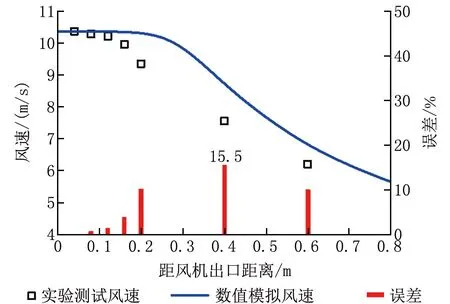
图5 数值模拟与实验结果对比

通过实验结果与数值模拟结果的对比可以发现,在射流的初始段实验结果与数值模拟结果相差较小。测点6处两者差异最大,相差15.5%。原因可能是实验中采用的射流风机结构简单,风机叶轮带动空气直接进行通风,没有任何的均流装置,导致风机射流在主体段(测点5～7)受到更多周围空气掺混的影响,形成与数值模拟中理想风机出流之间的速度差异。但考虑到射流风机对管廊的局部控制作用更重要,风机射流起始段(测点1～5)的误差都较小,认为所选的简化方式、数值模型及求解算法适用于管廊局部通风系统研究。

2 模拟结果

2.1 局部射流特征分析

选取换气次数为4 h-1的工况对管廊中设置局部射流风机后的流场特征进行分析,排风量为7 560 m3/h,进风温度为26 ℃。为了对比有无射流风机时管廊内流动状态对温度的影响,在射流风机的运行工况中,设定管廊排风速度为1.89 m/s(对应风量为0.9×7 560 m3/h),射流风机风速为2.31 m/s(对应风量为0.1×7 560 m3/h),两者风量相加与不设置射流风机的管廊总风量相等。截取管廊中心处纵截面,由于管廊长度比高度大很多,为了方便观察将纵截面云图按z∶y=1∶4的比例进行缩放,管廊截面温度与速度云图见图6。

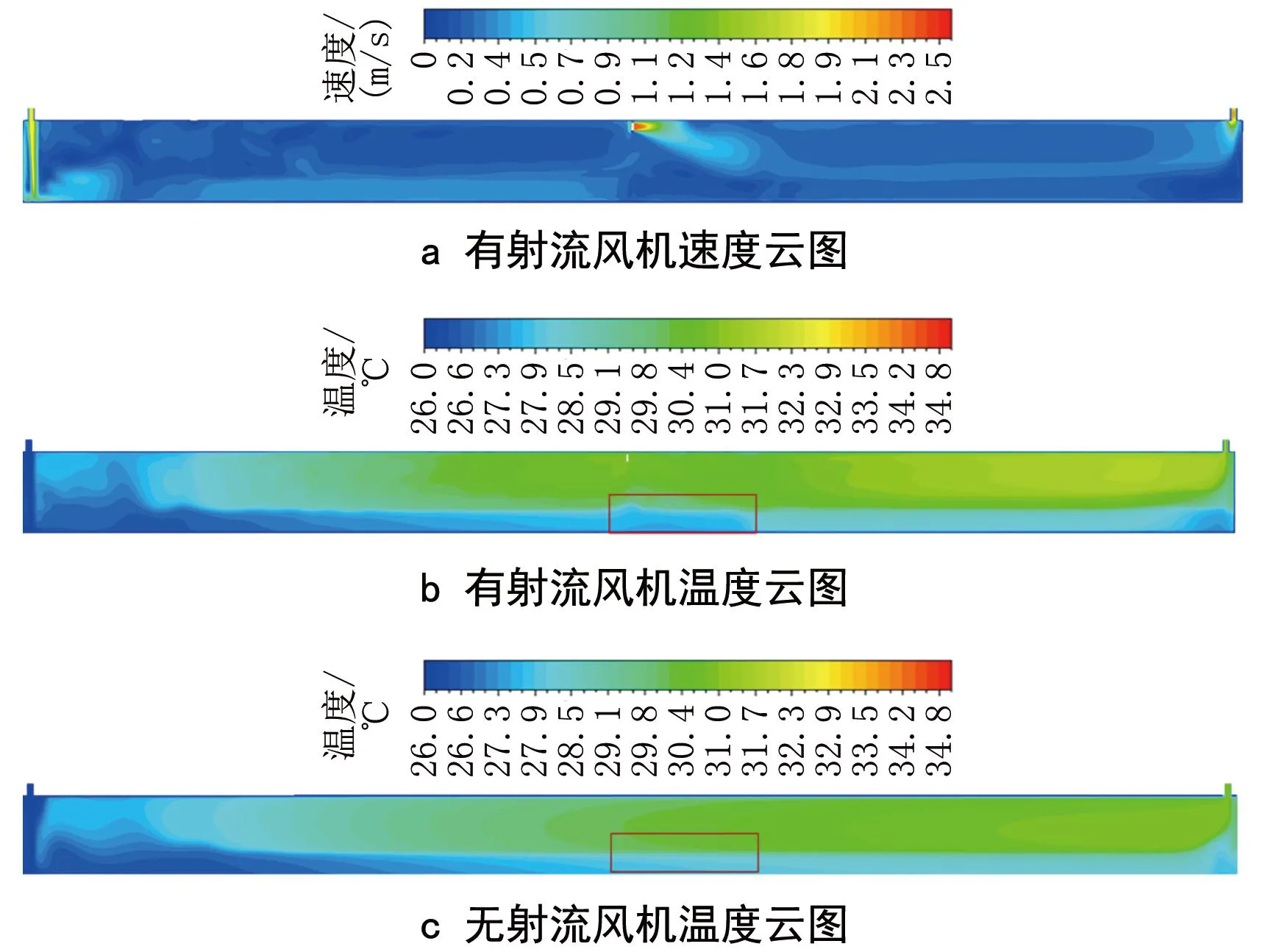
图6 有无射流风机纵截面温度云图与有射流风机速度云图

观察图6a可见,射流风机处相较于管廊全局风速较大,风机射流主体在运动过程中逐渐脱离管廊上壁面,冲击了底部的低速气流,使稳定的气流发生扰动。这种现象对温度场会产生影响,对比图6b和图6c可以看出,没有射流风机的工况中高温层逐渐蔓延至管廊底部,使得局部温度逐渐升高。设置射流风机后,温度层发生了改变,风机下部区域的温度降低,温度层高度维持稳定。对管廊断面的平均温度进行分析,计算方式为计算所选截面的每一个网格的温度与面积的乘积,累加后除以所选截面的面积,即

(4)

式中ta为截面平均温度,℃;m为网格数量;j为网格编号;tj为网格温度,℃;Sj为网格面积,m2。

与云图分布一致,在截面温度分布图(见图7)中,管廊100～125 m处的温度分布出现了局部下降的趋势,相比不加射流风机,风机出口段局部区域截面平均温度降低了0.5 ℃。结合图6b分析,原因是风机射流在运动过程中衰减,对周围气流产生卷吸作用,强化了局部流场扰动,增强了换热效果。但是,这种效果随着射流距离的增加而逐渐衰弱,超过一定距离后消失。故而加装射流风机确实会在风机前后实现局部降温,但影响距离有限。

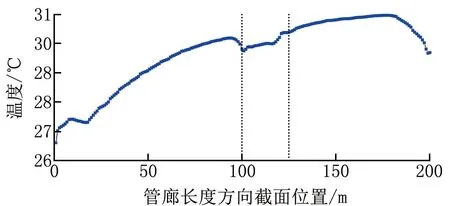
图7 纵截面平均温度

2.2 不同风量比分析

风速会影响射流的状态,为分析射流风速对管廊局部温度的控制效果,设置了不同的射流风速工况,如表4所示。其中,工况1～3中的排风量加射流风机风量相同,总风量为7 560 m3/h,风机风量占总风量的比例分别为5%、10%、15%。工况4与工况2的射流风机风速相同,排风量与工况2的总风量相同。不同工况的模拟结果如图8所示。

表4 工况速度设置参数 m/s

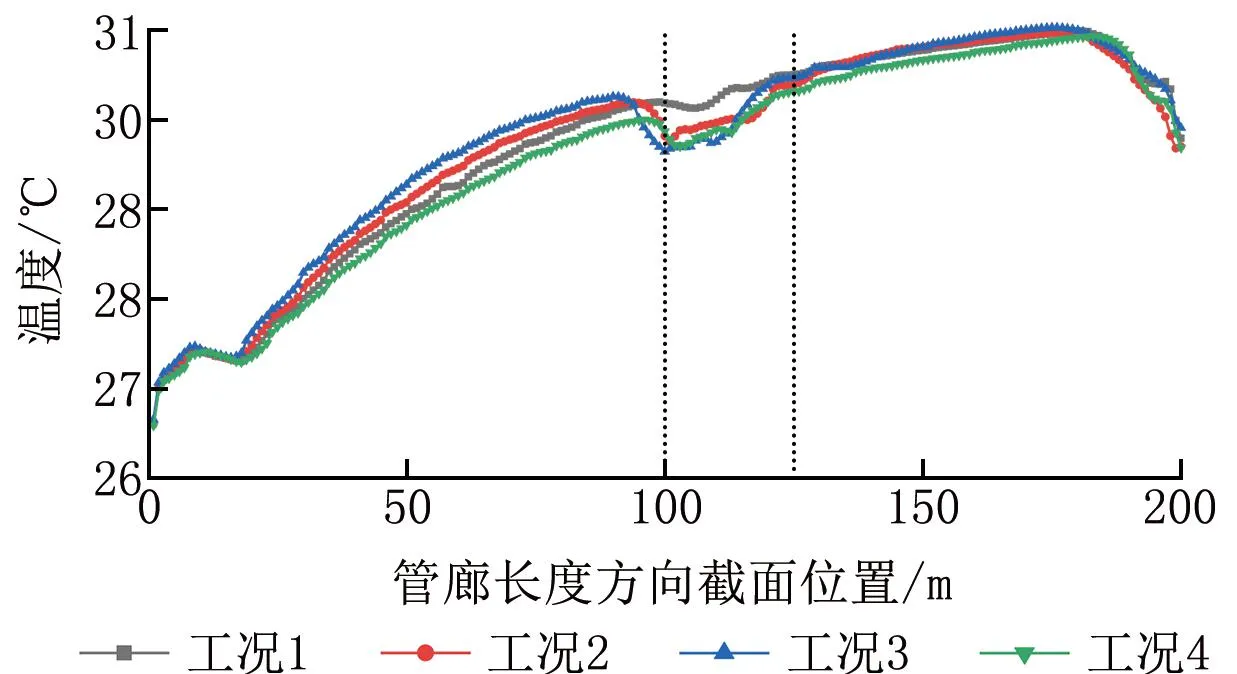
图8 不同工况截面平均温度

从管廊前段(0～100 m)温度分布来看,截面温度高低与进风口风量相关,进风口风量工况3<工况2<工况1<工况4。不同工况的前半段温度工况3最高、工况4最低。在射流风机作用区域,不同射流风速对风机的作用范围并无影响,均为25 m左右。而100～125 m处温度的下降趋势表明射流风机的风速对管廊局部散热有影响,当风机风量达到总风量的10%(工况2)时,再继续增大风速并不能带来散热效果的有效提升,此时应考虑增大换气次数来降低管廊温度。同时由于风机的作用区域长度并不随风机速度变化,应考虑射流风机风速的合理设定,避免动力源的浪费。

2.3 射流角度分析

如前所述,管廊射流风机作用区域温度降低的原因是风机造成气流扰动,那么改变风机出风角度,从而改变射流与壁面的碰撞形式,让气流在局部狭小空间形成贴附或撞击,加剧空气的扰动,可能会达成更好的控温效果。所以本文在工况1和工况2的基础上调整风机射流角度,设置0°、45°、90° 3个不同角度的工况,探究射流角度对管廊散热效果的影响,角度设置如图9所示。

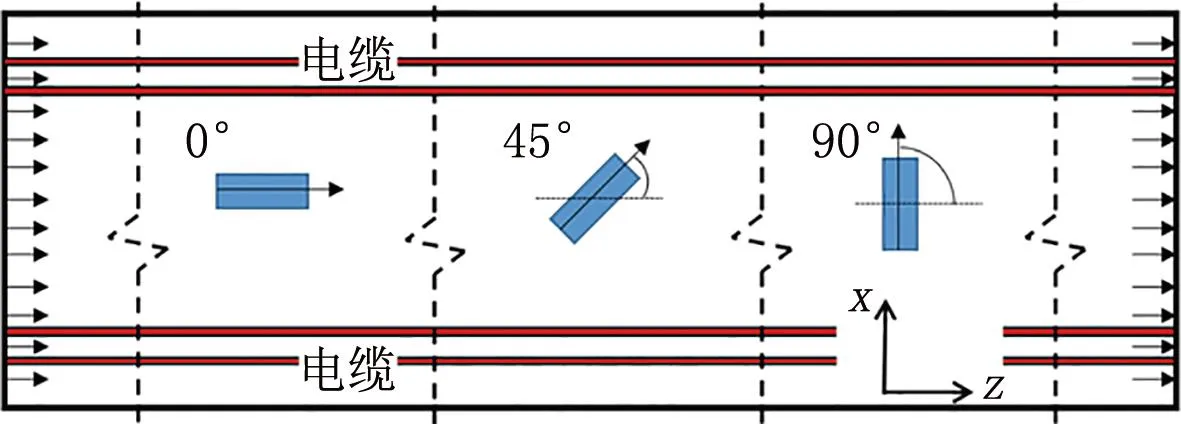
图9 风机射流角度示意图(顶视图)

选择工况2进行分析,由于管廊100～125 m的温度下降区域与射流风机控制区域重合,管廊射流风机后2 m和10 m分别位于风机射流的起始段和主体段,可充分反映这2个区域的温度和速度变化,具有代表性。选取z=102 m与z=110 m截面进行具体分析。图10显示了这2个截面的温度分布与速度方向。从图10可见,电缆附近的热浮升力引起的速度明显：在0°射流角度工况中,射流对电缆附近的气流速度影响较小;在45°射流角度工况中,射流对右侧电缆附近的气流影响较大,使得电缆附近的速度场与温度场发生改变,管廊内温度分布更加均匀;在90°射流角度工况中,射流对左侧电缆附近的气流影响较大。从温度分布可知,不同角度的射流能改变截面温度分布：在0°射流角度工况中,低温区域主要集中在底部;在45°射流角度工况中,z=110 m截面温度变得比较均匀;在90°射流角度工况中,z=102 m截面温度已经变得较为均匀。为了更好地分析温度的变化,选取不同截面的平均温度进行对比,如图11所示。

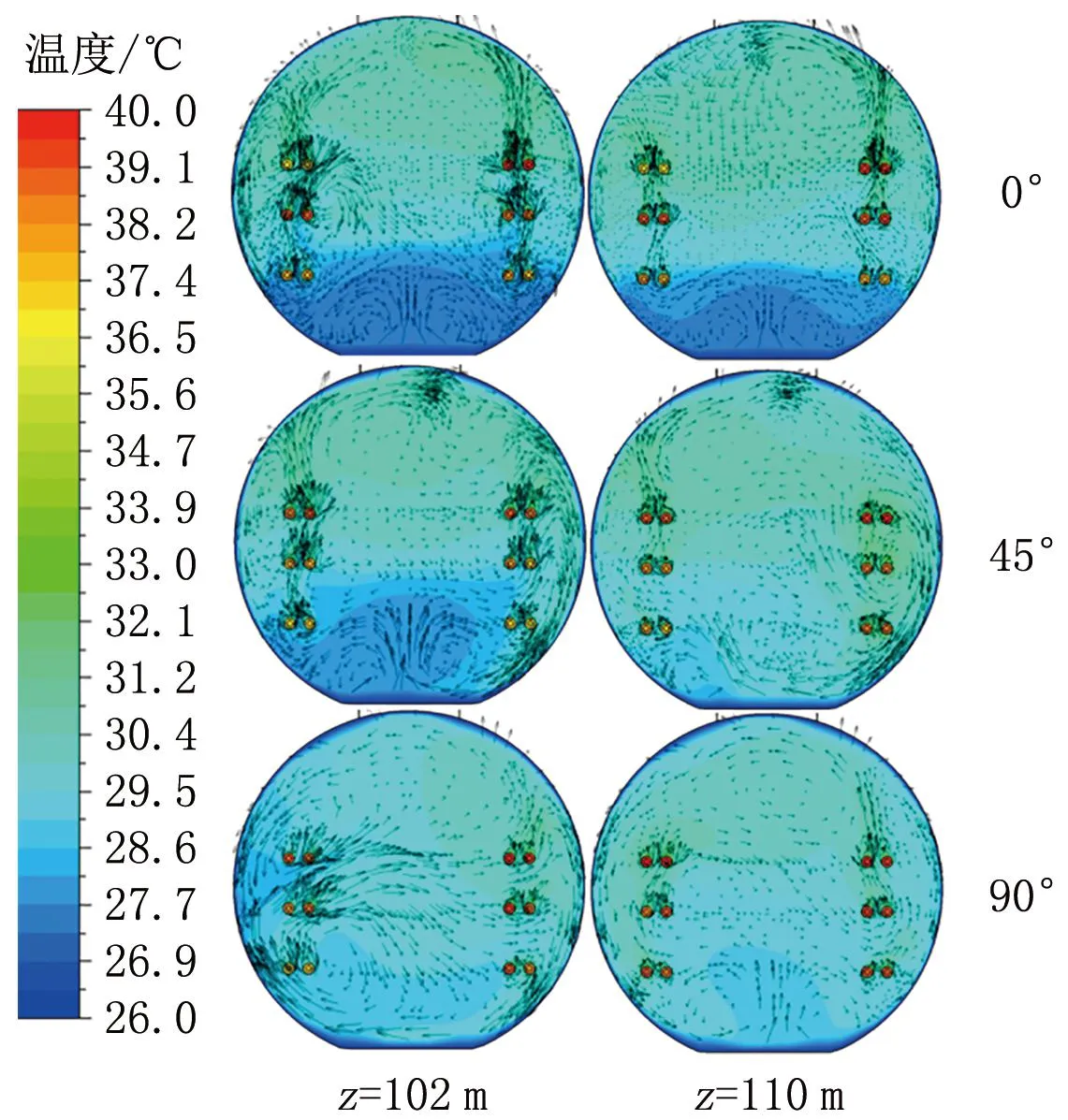
图10 不同射流角度时的速度方向与温度云图

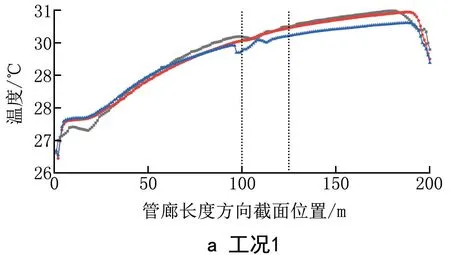
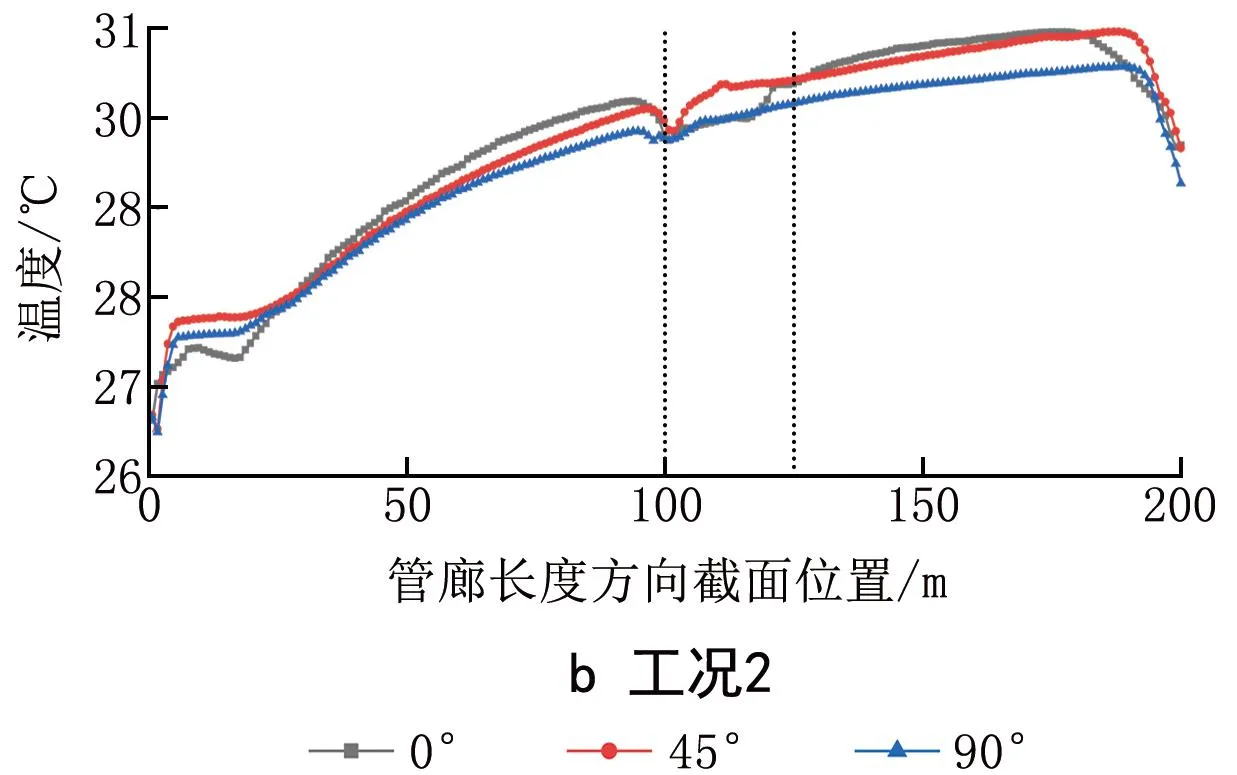
图11 不同射流角度截面平均温度

通过对比发现,工况1和工况2射流风机处均出现了局部温度降低的现象,风机作用区域都在25 m内。横向对比不同角度的模拟结果,发现射流角度为90°时降温效果更好。在射流风机作用区域内,射流风机风量增加带来的结果是换热增强,工况2在射流角度为0°、45°时的温度下降幅度要明显优于工况1,与前述结果吻合。射流角度为90°时,风机作用区域的温度下降趋势延伸到管廊后段,即125～183 m段,相比射流角度0°、45°工况管廊截面平均温度分别降低了0.41、0.33 ℃,取得了更好的降温效果。分析原因是高速射流冲击管廊壁面,狭窄的通风空间中产生了剧烈的空气扰动,90°的射流使得管廊旋转动量最大,衰减距离更长,持续冲击后段管廊的平稳层流,强化了后段的通风散热。由此可知,风机射流角度对管廊的通风散热会产生影响,存在较优的角度,最优射流角度为90°。

3 结论

本文通过数值模拟方法,利用局部通风的思路对200 m长电缆管廊进行了通风换热研究,使用1∶25 比例的缩尺模型验证了数值模型的可靠性,分析了电缆管廊在射流风机作用下的温度场和速度场,对比了不同管廊总风量、风机送风量、风机射流角度下的通风散热效果,所得结论如下：

1) 风机射流主体在运动过程中会逐渐脱离管廊上壁面,冲击底部的低速气流,使稳定的气流发生扰动,对温度场产生影响。设置射流风机后,管廊温度层发生了改变,风机下部区域温度降低。

2) 风机射流在运动过程中衰减,对周围气流产生卷吸作用,强化了局部流场扰动,增强了换热效果。加装射流风机会使风机前后温度降低,在风机出口段局部区域截面平均温度降低了0.5 ℃,但影响距离有限,作用区域长度约为25 m。

3) 风机射流角度对管廊的通风散热有较大的影响。当射流角度为90°时,在管廊的大部分区域降温效果都很好,对管廊后端的温度控制最佳,相比射流角度0°、45°工况管廊截面平均温度分别降低了0.41、0.33 ℃。