含固氧颗粒的液氢传输管路中静电积聚仿真研究

田雪皓,刘柏文,王磊,马原,厉彦忠,雷刚,陈强

(1. 西安交通大学制冷与低温工程系,710049,西安;2. 航天低温推进剂技术国家重点实验室,100028,北京)

液氢具有高比冲、无污染等特点,在航天和能源领域的应用日益广泛[1]。但是,液氢易燃易爆且高度电绝缘,在输送过程中易产生静电起电,造成安全隐患[2]。同时,液氢作为深冷介质,其工作温度远低于空气凝固点。在进行液氢加注、排空等操作时,空气易渗入并形成固空颗粒[3]。由于氮在液氢中的溶解度更高,积累的固空多为富氧或固氧颗粒[4-5]。固体颗粒与管壁碰撞产生静电电荷,即摩擦荷电。当电荷累积到一定程度时,可能导致火花放电引发爆炸[6-7],若固空颗粒中氧比例较高,甚至可能发生爆轰[8-9]。因此,明确固空颗粒在液氢管流中的静电积聚规律与边界对液氢输送系统的静电防护尤为重要。

目前,液氢的静电特性已引起学者关注。Cassutt等[10]通过实验证明了液氢在储存和输运中会产生显著的静电积聚,且液氢极低的电导率导致电荷难以耗散。Liu等[11]建立了电场与流场耦合理论模型,仿真得到液氢中电荷密度约为10-12C·m-3。携带固空颗粒的液氢管流中,固液两相流动特性对研究静电积聚具有重要影响。目前,固-液两相流的研究对象包括工业领域的管道流、流化床等,常用数值方法有连续法和离散法[12]。其中,连续法较典型的为双流体模型,而离散法则包括拉格朗日颗粒轨道(Lagrangian particle tracking, LPT)方法和离散单元法(discrete element method, DEM)[12]。在研究稀疏颗粒的运动,即颗粒相体积分数小于5%时,多采用LPT方法[12]。在处理密相颗粒运动时,通常采用DEM方法。Tsuji等[13]利用LPT法对提升管内颗粒的聚团行为进行了研究,并与Tsuo等[14]用双流体模型得到的结果做了对比,结果表明:两种模型得到的气体速度等影响因素对模拟结果的影响趋势相同,但LPT法得到的结果中颗粒聚团更频繁,更符合实际过程。上述方法对相间耦合作用和颗粒间作用均有相关描述,但要实现对颗粒荷电的仿真预示仍面临较大挑战[15]。

摩擦荷电的本质是两种不同材料接触表面电荷的转移,包括电子、离子和材料转移等[16]。对于气力输送过程中的颗粒荷电问题,Harper[17]指明,因材料功函数的不同而产生的接触电势差是电荷转移的驱动力。Murata[18]、Mehrani等[19]提出了光电发射、表面态等不同的荷电机理。但是,在颗粒碰撞与分离过程中,电荷传递微观过程与荷电机理仍不明确。电子转移机制认为,金属间的接触荷电理论与费米能级和功函数相关,电子通过量子力学的隧道效应进行转移,金属-绝缘体的荷电理论与绝缘材料的等效功函数有关,但绝缘体间的荷电理论尚无定论。离子和材料转移机制分别认为,物质表面水分子层中的离子和物体碰撞摩擦造成的表面磨损导致了电荷交换[16,20]。根据电荷交换载体不同,所建立的荷电模型包括:电容器模型[16],外加电场下的电荷转移模型[21],水合离子电荷转移模型[22]和表面状态模型等[16]。微观尺度的研究有助于揭示电荷的内在转移规律,完善颗粒荷电机理,而宏观尺度的研究对颗粒流动带电行为的监测和控制具有价值。两相流动中颗粒群的电荷积聚过程并非单颗粒碰撞的简单叠加,流场不仅起到动力源作用,也通过双向耦合影响颗粒行为,使颗粒群的荷电过程更为复杂。在实验层面,Watano[23]发现,随着输送气流速度增加,颗粒电荷在达到饱和前会持续增加,而Nifuku等[24]的结果显示,颗粒比电荷(单位质量颗粒带电量)随流速增加存在极值。实验结果的不可重复性归因于颗粒电荷对环境因素的敏感性,实验初始和边界条件难以控制。在理论层面,Tanoue等[25]的结果显示,颗粒电荷随Re增加而减少,但Grosshans等[26]的结论与之相反,说明不同荷电模型对应的电荷交换载体对荷电过程的影响不同。Lim等[27]发现,静电力对颗粒行为的影响不大,而Grosshans等[28]的研究表明,静电力主导颗粒的涡旋运动。Li等[29]的结果显示,St数高的颗粒更易受到静电的影响。理论计算结果同样不具备广泛的一致性,这是因为单个荷电模型无法涵盖所有作为电荷交换的载体,潜在的荷电机理仍没有被完全揭示。其中,由电容器模型得到的理论数据与实验的验证性较好,也被多数学者采纳。

两相流动电荷积聚研究中,对于液氢这种低黏度、低密度、低电导率的低温流体研究较少,固氧/固空颗粒等低温物质的电学性质难以测量,而液氢加注工艺流程的静电防护对运行安全性尤为重要。因此,研究低温液氢中固氧颗粒在输送过程中产生静电的积聚效应及分布特点,建立静电积聚的数理模型,并获得定量的积聚规律特性,为提出抑制或消除管内颗粒静电积聚的方法和措施提供理论依据,减小由于颗粒输运过程中静电积聚产生的危险性,对于控制监测颗粒电荷积聚具有重要指导作用。本文研究湍流、颗粒和管道间复杂的相互作用及液氢管路静电积聚规律与边界,通过参数化研究分析固氧颗粒电荷演化过程的积累效应以及电荷积聚的影响因素和分布规律。

1 数值模型建立

本文建立了拉格朗日颗粒轨道法与计算流体动力学(computational fluid dynamics, CFD)的耦合模型,并采用电容器模型对液氢管路中固氧颗粒的起电过程开展仿真研究。含固氧颗粒的液氢管内固液两相流物理模型示意图如图1所示。其中,水平传输管长为L,半径为R,液氢携带固氧颗粒以流速uinlet流入,从右侧排出。固氧颗粒速度为up,带电量为Q。

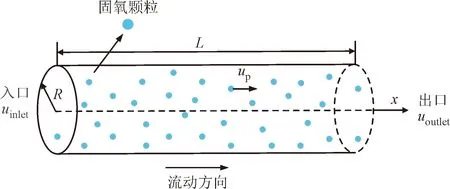
图1 含固氧颗粒的液氢管流示意 Fig.1 Schematic diagram of liquid hydrogen pipe flow with solid oxygen particles

1.1 流体-颗粒动力学模型

将液氢视为不可压连续介质。在欧拉坐标系框架下,采用Navier-Stokes方程描述液氢流动过程,并通过相间相互作用与颗粒相耦合。由于液氢管路中渗入空气量较少,固氧颗粒量较少[5],颗粒体积分数与流体相比可忽略,因此在控制方程中不引入颗粒相体积分数。流体质量和动量方程表示为

(1)

(2)

式中:u、p、ρ、ν、Fs分别为流体速度、压力、密度、运动黏度和颗粒对流体体积力。

假设颗粒由相同材料、刚性、单分散、单组分的稀疏球形颗粒组成,选用LPT法对固液两相流开展仿真[12]。其中,每一个固氧颗粒均可被示为一个质点,运动方程通过牛顿第二定律[30]得出

(3)

式中:fg、fcoll分别表示由重力和碰撞引起的加速度;∑fp包括颗粒所受曳力、浮力、静电力、压力梯度力、虚拟质量力、Saffman力、Basset力等引起的加速度,但与颗粒本身惯性相比,静电力、Basset力对颗粒行为的影响很小,通常可以忽略[30]。

单个固氧颗粒所受曳力[26]为

(4)

式中:Cd为曳力系数;urel表示滑移速度。曳力系数与颗粒雷诺数Rep=2|urel|rp/ν的关系[26](rp为颗粒半径)如下

(5)

颗粒间碰撞为完全弹性碰撞,不考虑碰撞造成的速度、能量损失。颗粒与壁面间是不完全弹性碰撞,碰撞后颗粒法向速度改变

u′p,n=-keup,n

(6)

式中:ke为恢复系数。

1.2 颗粒荷电模型

对于金属-绝缘体碰撞,通常采用电容器模型[16]。该模型假设电子转移是电荷交换的主要方式,并将颗粒与壁面的接触区视为电容器,如图2所示。

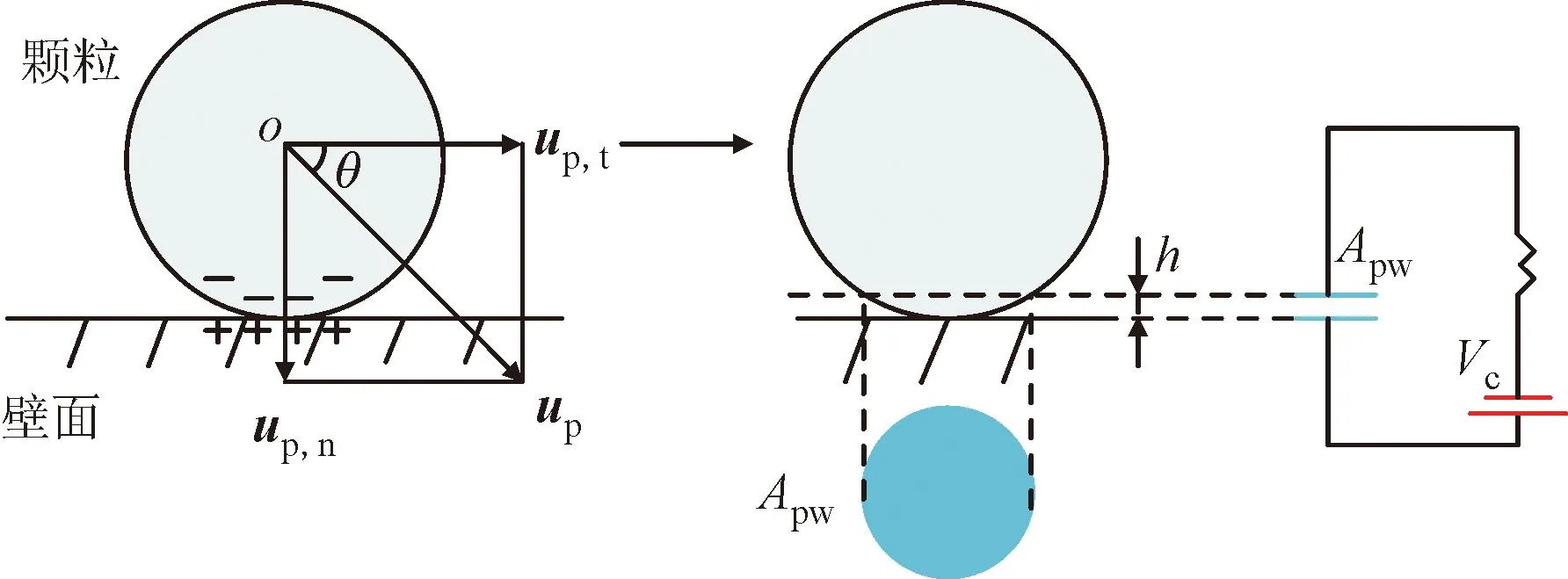
图2 粒壁碰撞示意Fig.2 Schematic diagram of particle-wall collision

电容器模型采用接触体表面功函数差Vc驱动电子转移,与接触体几何因素相关的电容间隙h由电子转移的临界距离决定,接触面积Apw用于计算电荷交换面积以及接触电容。颗粒与壁面分离后,得到电子的颗粒带负电,交换的电荷从碰撞区域均匀扩散至整个颗粒表面。液氢管路中固氧颗粒与管壁的碰撞视为金属-绝缘体碰撞,并且液氢系统温度恒定为20 K,温度对材料物性及电荷交换的影响可忽略[16]。因此,本文可采用电容器模型计算两相流中颗粒的电荷积聚。

固液两相输送过程发生两类电荷交换,包括颗粒间碰撞引起的电荷扩散和颗粒-壁面碰撞引发的电荷转移。颗粒i和颗粒j接触期间,各自电荷交换量ΔQi和ΔQj[26]为

(7)

式中:Ci、Cj、τpp、Δtpp分别为颗粒i、j的电容、颗粒电荷弛豫时间和接触时间,可按照下列公式确定

Ci=4πε0rp,i

(8)

(9)

(10)

(11)

αij=

(12)

其中,ε0为真空介电常数,Aij为颗粒接触面积,φp为颗粒电阻率,up,ij为颗粒间相对速度,αij为颗粒接触系数,vp和Ep分别表示颗粒泊松比和杨氏模量。

有别于颗粒间碰撞,颗粒与壁面碰撞的电荷交换量ΔQpw由动态电荷转移ΔQc和预电荷贡献ΔQt组成[26,31],ΔQc和ΔQt分别与材料和颗粒电荷有关。ΔQpw的定义为

ΔQpw=ΔQc+ΔQt

(13)

ΔQc=CVc(1-e-Δtpw/τpw)

(14)

(15)

式中:C、Vc、Δtpw、τpw和αpw分别为接触电容、接触电位差、粒壁接触时间、电荷弛豫时间和碰撞系数,可按照下列公式确定

(16)

(17)

τpw=εε0φp

(18)

(19)

Apw=πrpαpw

(20)

其中,Apw为接触面积,vw和Ew分别为壁面泊松比和杨氏模量,ε为壁面相对介电常数。

颗粒间相互碰撞不会产生新的电荷,仅会交换原有电荷;颗粒与壁面碰撞产生新的电荷,并且由于颗粒-流体、流体-壁面之间的电荷交换可忽略,粒-壁碰撞也是固液两相流中颗粒带电的唯一来源[32]。

粒壁间电荷交换由不同材料间的接触电位差Vc驱动[16],其表达式为

(21)

式中:Vp、Vw分别为颗粒和壁面材料的表面功函数,等号右侧第3项表示由颗粒荷电后引起的附加电势差。

颗粒和壁面材料的功函数决定了电荷积聚程度。功函数是将电子从固体内部转移到表面外一点所需的最小能量。对于固氧颗粒,可利用Materials Studio软件计算其物性。本文通过比较固氧晶体费米能级与远离晶体表面的静电势计算固氧功函数。由于固氧凝固后随温度降低形成不同的晶体结构,导致晶格参数(a～Vm)发生改变,本文根据表1数据构建20 K液氢系统中固氧α-O2晶胞[33]。由于功函数对晶体结构和表面取向具有较大依赖性,首先需要依据能量守恒对固氧晶胞进行分子、几何优化以忽略晶体表面松弛的影响。随后,切割晶胞形成单面分子层并构建间隔20×10-10m真空层的堆积阵列,以忽略真空层两侧分子层的静电相互作用。最后,根据堆积体系静电势的空间分布可得到固氧α-O2的功函数约6.37 eV。此外,本文通过上述方法得到金属铬Cr的功函数为4.46 eV,与标准值(4.5 eV)的误差不到1%。因此,该方法能够准确计算材料功函数。

表1 20 K下固氧α-O2的晶胞结构[33]

1.3 模型设置

本文取管长为2 m、管径为10 mm的水平管为参考工况,研究含固氧颗粒液氢管流的静电积聚规律。采用COMSOL Multiphysics软件建立水平管三维模型。设置速度入口、压力出口,无滑移壁面边界条件,管壁接地以导出壁面电荷,该处理不影响颗粒电荷积聚饱和值。颗粒以与流体相同速度注入,颗粒数由颗粒质量确定。

在固液两相流模拟中,时间步长Δtp通常取Rayleigh时间步长ΔtR的10%～40%以满足精度要求[34]。本文采用Rayleigh时间步长的30%,即8×10-7s进行仿真计算。其中,Rayleigh时间步长根据最小颗粒尺寸计算,计算公式为

(22)

式中:Gp为颗粒剪切模量。

1.4 模型验证

本文建立了网格单元数分别为21万、84万、119万和166万的4套模型,根据颗粒比电荷Qsc和平均冲击电荷ΔQpw(电荷交换量)评价网格的适用性,结果如图3所示。可以看出,采用119万网格单元模型满足要求。

图3 网格数对数值计算结果的影响Fig.3 Influence of grid number on numerical results

图4给出了单个聚四氟乙烯(PTFE)颗粒与黄铜板碰撞带电过程预测结果,并与Grosshans等[35]和Matsuyama等[36]的数据进行了比较。图4(a)显示了颗粒电荷Q和冲击电荷ΔQpw的演变过程,平均误差分别为1.59%、4.76%。图4(b)显示了冲击电荷ΔQpw随颗粒初始电荷的变化规律,计算结果遵循Matsuyama等[36]提出的线性曲线,与实验数据的平均误差为13.18%。

(a)颗粒电荷和冲击电荷的演变过程

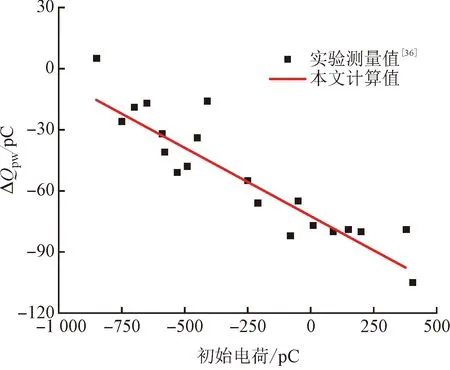
(b)初始电荷对冲击电荷的影响

针对固液两相流电荷积聚,本文选用Watano[23]数据作为比较依据,结果如图5所示,研究对象为气力输运水平管道中2.5 g聚甲基丙烯酸甲酯(PMMA)颗粒的电荷积聚过程,颗粒带负电。可以看出,颗粒比电荷Qsc随Re增加存在极大值。数据平均误差为7.22%,最大误差为18.40%。综合来看,本文所构建模型能够表征固氧颗粒的电荷积聚规律。

图5 颗粒比电荷随雷诺数的变化规律Fig.5 Variation of particle specific charge with Re

2 结果与讨论

本文模拟流体相为液氢、固体相为α-O2的固氧颗粒,温度为20 K。表2提供了用于模拟含稀相固氧颗粒的液氢水平管参数。由于颗粒表面电位极性不确定,本节颗粒电荷以绝对值给出[35]。其次,本研究中颗粒相体积分数最大值为4.9%,小于5%,满足LPT法的使用条件[12]。

表2 模拟所用的含稀相固氧颗粒的液氢水平管参数

2.1 固液两相流动电荷积累效应

图6(a)展示了带电颗粒在液氢管流中的分布。可以看出,进口处多数颗粒不带电,经过与壁面碰撞起电和颗粒间电荷交换后,出口处带电颗粒增多,带电量增强。图6(b)展示了不同位置4个径向截面的颗粒电荷分布,图中r为颗粒距管道中心轴的距离,R为管道半径。可以看出,壁面区域颗粒电荷远高于流动核心区域,并通过颗粒间碰撞向核心区传递电荷,且随着流动距离增加,整体带电量上升。此外,颗粒电荷随流动距离增加逐渐达到饱和,近壁区的颗粒由于频繁的粒壁碰撞率先饱和。由图6(b)可知,固氧颗粒积聚饱和电荷量约为84 pC。

(a)带电颗粒几何分布

(b)颗粒电荷随径向分布情况

当液氢流速为10 m·s-1时,大部分颗粒携带电荷较少,液氢管流中稀相固氧颗粒的平均电荷Qav约为10 pC。将稳态下管内颗粒电量和与管路总体积相比[37]可知,单位体积液氢中固氧颗粒电荷量为2.84×10-4C·m-3,较纯液氢大8个数量级[11]。因此,含固氧颗粒液氢管流的静电防护面临更严峻的挑战。

静电电荷随时间和位移不断积累[38],当出口颗粒总电荷Qout达到安全阈值时,可能引发静电危害。图7展示了不同管长的出口电荷Qout随时间变化规律。可以看出,出口电荷Qout随颗粒群的流动逐渐增加并趋于稳定。管道越长,粒壁碰撞次数越多,出口电荷Qout越大,稳定后的出口总电荷Qout分别约为551、1 204、2 233 pC,与管长近似成正比。因此,长管道的安全威胁更大。另外,曲线在入口段的斜率较小,这是由于颗粒释放后需经历随机扩散才能与壁面碰撞。

图7 不同管长的出口电荷随时间变化规律Fig.7 The change of outlet charge of different tube lengths with time

2.2 固液两相电荷积聚影响因素

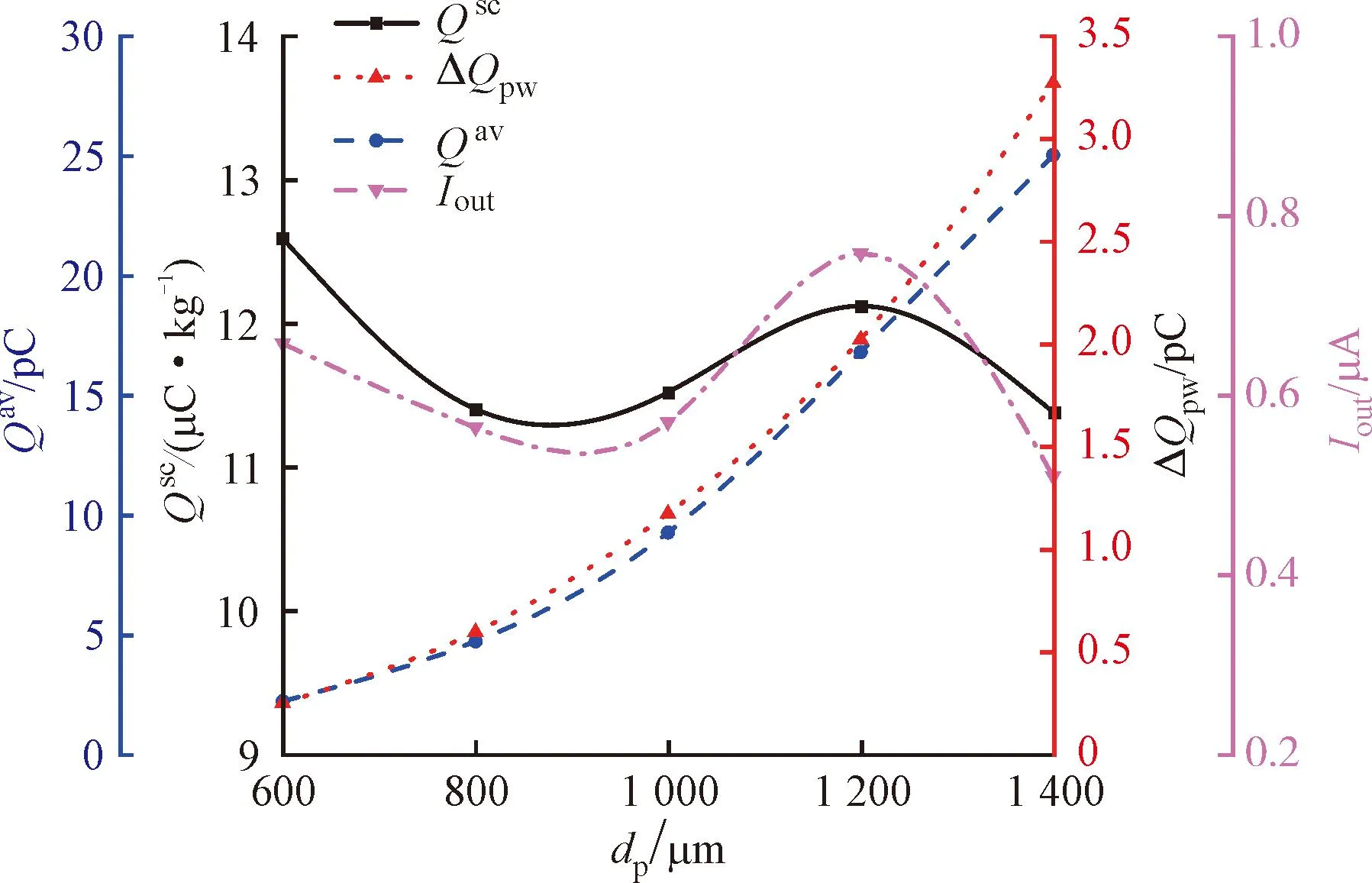
图8 粒径对电荷积聚的影响Fig.8 Effect of particle diameter on charge accumulation

图8显示了出口比电荷Qsc、平均冲击电荷ΔQpw、出口粒子平均电荷Qav、出口电流Iout4种统计参数随固氧粒径的变化规律。可以看出,随着粒径增大,颗粒电荷Qav和冲击电荷ΔQpw增大,比电荷Qsc和电流Iout存在极小值和极大值。由图可知,颗粒电荷Qav对粒径非常敏感,且随着粒径增加,颗粒电荷增长趋势加快。由式(17)、(20)可知,粒径与接触面积、时间正相关,故冲击电荷ΔQpw和颗粒电荷Qav随粒径增大而增大。同时,当颗粒质量流量一定时,粒子数随粒径增大逐渐减少,所以比电荷Qsc和电流Iout存在极小值和极大值。比电荷Qsc的极小值、极大值分别为11.29、12.12 μC·kg-1,电流Iout的极小值、极大值分别为0.54、0.76 μA。此外,静电危害通常源于颗粒放电能量过高[39],所以静电安全性往往由颗粒电荷Qav决定。综上可知,大尺寸固氧颗粒电荷Qav更大,建议通过布置滤网减小颗粒粒径的方法提高运行安全性。

图9展示了沿程冲击电荷ΔQ(即整个管道内粒壁碰撞所产生的电荷交换)和颗粒出口电荷Q的概率密度函数(probability density function,PDF)。PDF反映了所求数值统计次数与总数的比值。

图9(a)为沿程冲击电荷ΔQ的概率密度分布。可以看出,每条曲线均呈现左低右高的趋势,且粒径增大,曲线右移。据图4(a)可知,冲击电荷随碰撞次数增多逐渐降低。所以,图9(a)中每条曲线右侧较大的冲击电荷对应初期碰撞所发生的电荷交换,左侧则对应后期碰撞。并且,限于管长,粒壁碰撞大多属于初期碰撞,故曲线右侧PDF更大。同时,粒径越大,接触面积、时间越大,冲击电荷越大,曲线越接近右侧。

图9(b)为出口电荷Q的概率密度分布。可以看出,曲线存在波峰,且粒径增大,波峰右移,即颗粒电荷Qav增大,与图8趋势相符。并且,限于管长,颗粒普遍发生0～20次碰撞,如图10所示,使得大多颗粒电荷处于相同范围,故图9(b)存在波峰。

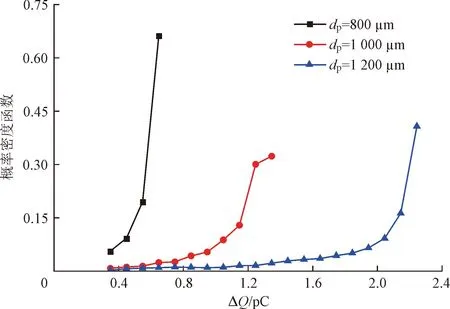
(a)沿程冲击电荷的概率密度分布

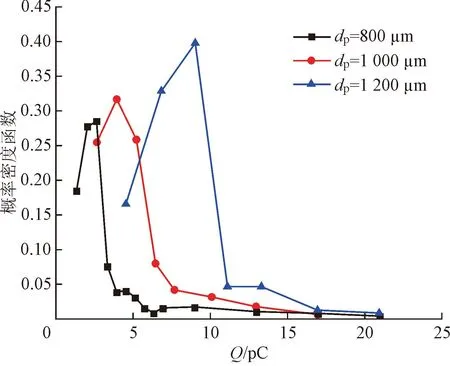
(b)颗粒出口电荷的概率密度分布

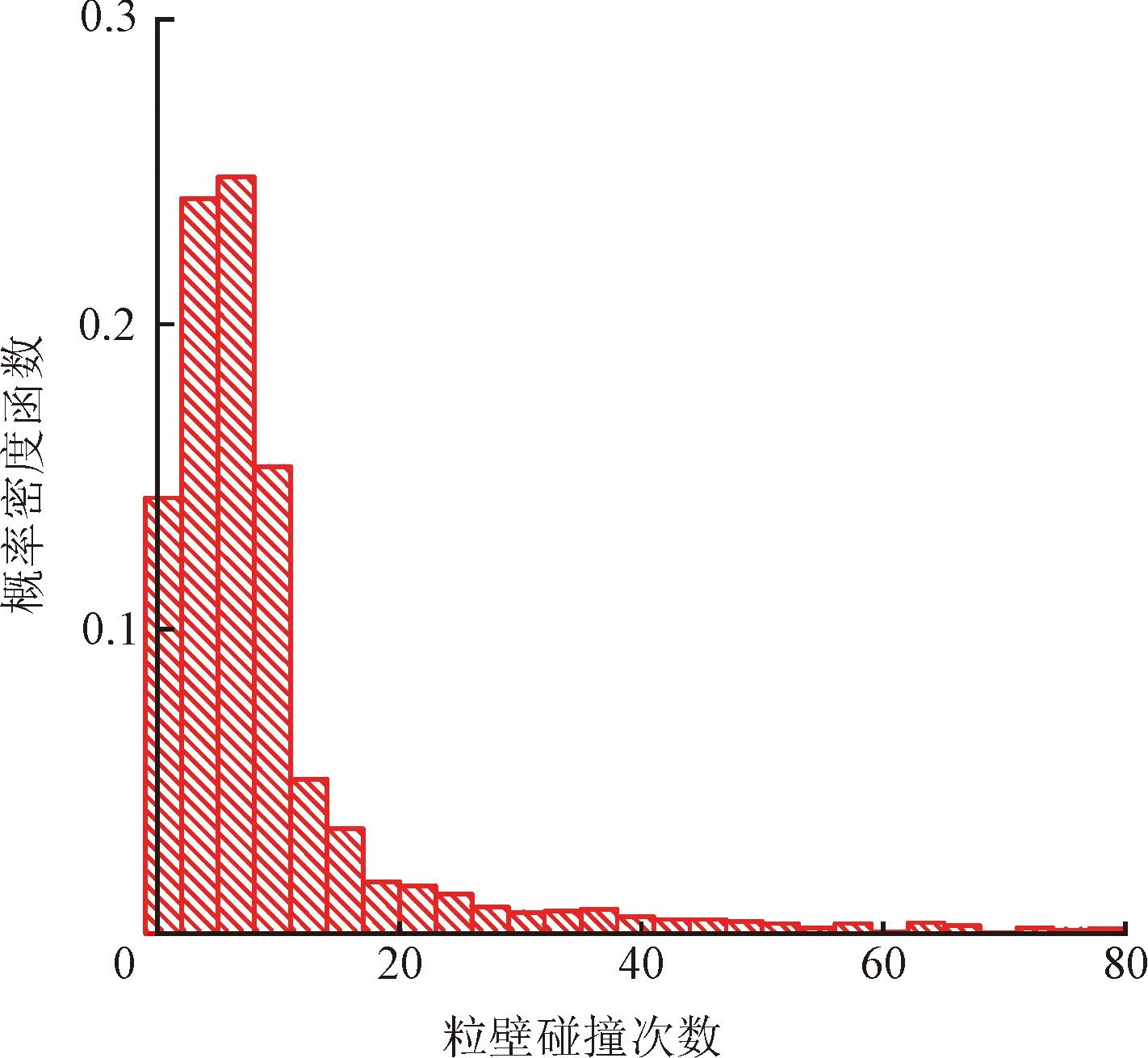
图10 粒壁碰撞次数直方图Fig.10 Histogram of the number of grain wall collisions

图11显示了4种统计参数随颗粒质量流量的变化规律。可以看出,随着颗粒质量流量增加,比电荷Qsc和颗粒电荷Qav略有减小,这是由于粒子数增多导致颗粒间碰撞更频繁,颗粒轨迹被限制,难以与壁面碰撞。同时,平均冲击电荷ΔQpw几乎不变,因为粒子数增加不会影响碰撞剧烈程度。另外,出口电流Iout增加与单位体积粒子数的变化有关。综上可知,需做好防漏和静电防护,密切关注固氧颗粒的形成与电荷积聚。

图11 颗粒质量流量对电荷积聚的影响Fig.11 Effect of particle mass flow on charge accumulation

图12显示了4种统计参数随管长的变化规律。可以看出,随着管长增加,比电荷Qsc、颗粒电荷Qav和出口电流Iout逐渐增大,且增幅逐渐降低,与图4(a)趋势类似。随着粒壁碰撞次数增多,颗粒电荷逐渐饱和,冲击电荷ΔQpw降低。因此,长管道电荷积聚更为严重。为提高运行安全性,实现降低颗粒电荷Qav的目的,可增设导电银网、接地线等装置导出电荷,以降低导电装置间的管道长度。

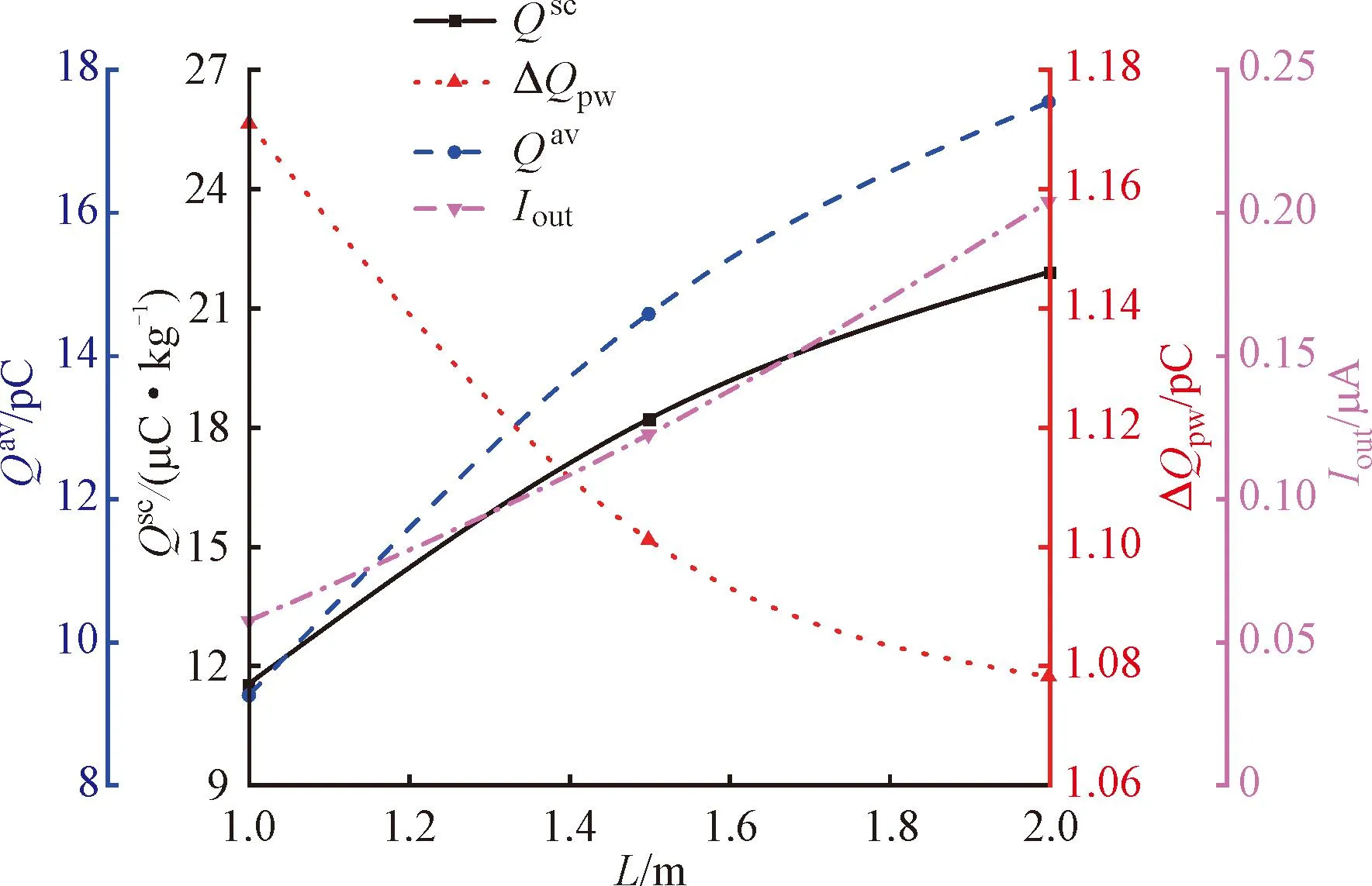
图12 管长对电荷积聚的影响Fig.12 Effect of tube length on charge accumulation

图13显示了4种统计参数随管径的变化规律。可以看出,随着管径增加,比电荷Qsc、颗粒电荷Qav和出口电流Iout减小,平均冲击电荷ΔQpw基本不变。根据理论分析可知,随着管径增加,颗粒由于重力沉降并与壁面碰撞的速度增大,冲击电荷随之增大,但粒壁碰撞概率和电荷交换次数随之降低。然而,图13显示冲击电荷变化并不大。这是由于本文采用的电容器模型中,冲击电荷仅取决于颗粒速度。颗粒轴向速度远大于径向速度,沉降带来的影响可忽略。因此,管径对碰撞速度的影响较小,管径主要通过碰撞次数影响电荷积聚。

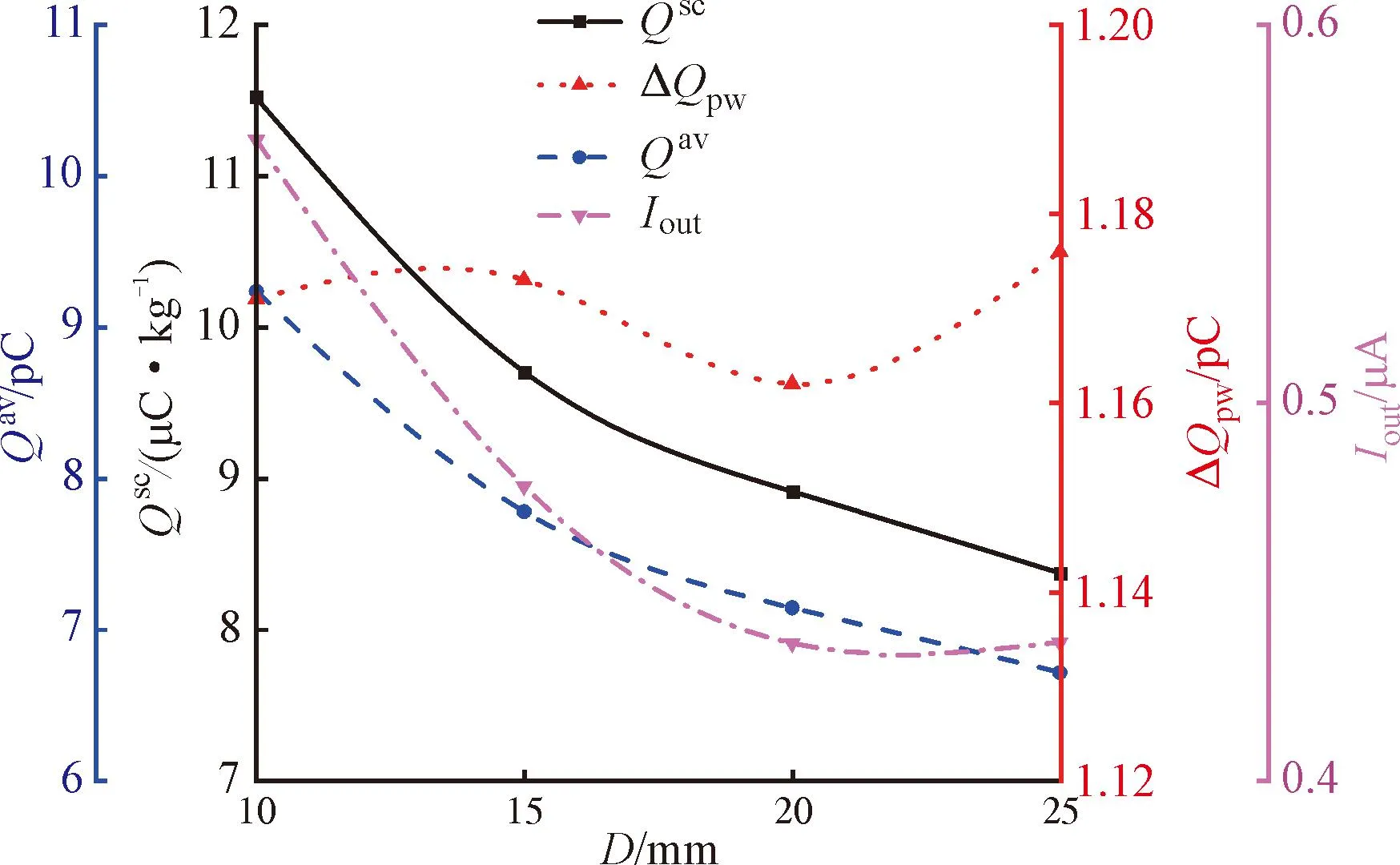
图13 管径对电荷积聚的影响Fig.13 Effect of pipe diameter on charge accumulation

图14显示了4种统计参数随流速的变化规律。可以看出,随着流速增加,比电荷Qsc和颗粒电荷Qav存在极小值,冲击电荷ΔQpw单调增加,出口电流Iout单调减小。当流速从10 m·s-1增至20 m·s-1时,粒壁碰撞更剧烈,颗粒电荷Qav增加;流速降至5 m·s-1时,颗粒在管道内停留时间和碰撞次数增多,颗粒电荷Qav同样增加。因此,颗粒电荷Qav和比电荷Qsc随流速增加存在极小值,分别为9.15 pC、11.41 μC·kg-1。此外,出口电流Iout=nqv0s,其中,n、q、v0、s分别指单位体积粒子数、颗粒电荷、颗粒速度及管道截面积。当颗粒质量流量一定时,随着流速增加,颗粒群更分散,n值降低,出口电流Iout随之降低。

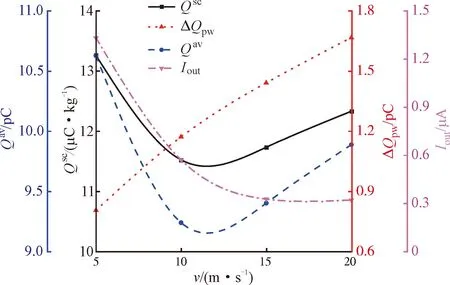
图14 流速对电荷积聚的影响Fig.14 Effect of velocity on charge accumulation

表3展示了颗粒物性对电荷积聚规律的影响。通过静电模型可以推断,杨氏模量Ep、电阻率φp、密度ρp对荷电过程影响最大。当杨氏模量增大时,材料形变减小,接触时间缩短,颗粒电荷降低;当电阻率增大时,电荷交换受到抑制,颗粒电荷降低;当密度增大时,颗粒由于重力作用与壁面的碰撞更剧烈,颗粒电荷增大。PTFE、固氧、PMMA的杨氏模量和电阻率依次增大,密度依次减小,能够对上述分析进行验证。表3中的模拟结果显示,颗粒电荷随杨氏模量、电阻率的增加和密度的降低逐渐减少,与上述分析完全相符。

表3 颗粒物性对电荷积聚的影响

3 结 论

本文针对含固氧颗粒的液氢管路中静电积聚规律及影响因素开展了仿真预示,所得结论如下。

(1)在固氧颗粒-壁面的碰撞与分离过程中,电荷传递的微观过程是电子在接触电势差驱动下进行转移。在液氢流速为10 m·s-1的工况下,液氢管流中稀相固氧α-O2颗粒的积聚比电荷Qsc约为10 μC·kg-1,颗粒电荷Qav约为10 pC,出口电流Iout约为0.5 μA。同时,两相流的电荷密度为2.84×10-4C·m-3,较纯液氢流大8个量级。

(2)固液两相流动中,电荷积累效应包括颗粒电荷随时间和位移的变化规律。管道出口处的颗粒总电荷Qout随颗粒群的流动逐渐增加并趋于稳定。另外,壁面区域的颗粒电荷远高于流动核心区,并通过颗粒间碰撞向核心区传递电荷。颗粒电荷随流动距离增加逐渐饱和,在固氧颗粒粒径为1 000 μm的工况下,颗粒积聚饱和电量约为84 pC。

(3)当颗粒质量流量一定时,比电荷Qsc随着粒径的增加存在极小、大值,分别为11.29、12.12 μC·kg-1;当粒径一定时,比电荷Qsc随着颗粒质量流量的增加略有降低;当颗粒物性一定时,比电荷Qsc随管长增加和管径降低逐渐增大,且随流速的增加存在极小值,为11.41 μC·kg-1;颗粒物性对电荷积聚的影响主要体现在颗粒杨氏模量、电阻率和密度上。