ODS MA754合金传热界面接触热阻实验研究

杨万奎,郭啸宇,曾和荣,郭玉川,唐彬,王冠博,严睿豪,孟兆明,郭斯茂

(1. 中国工程物理研究院核物理与化学研究所,621900,四川绵阳;2. 黑龙江省核动力装置性能与设备重点实验室,150001,哈尔滨; 3. 哈尔滨工程大学核科学与技术学院,150001,哈尔滨)

运行在高真空、微重力环境中的空间反应堆系统较难采用回路强迫对流换热的输热方式,而是以热传导和辐射换热进行热量传递与输送为主,因此,空间反应堆通常采用热管堆等全固态反应堆的堆芯设计[1-3]。固态反应堆内材料表面间的相互接触往往局限于接触面上的离散点或离散面,其他部分为真空辐射导热,由此会形成接触换热的附加阻力,即接触热阻(thermal contact resistance, TCR)。准确获取反应堆结构部件接触界面的接触热阻,对结构热力学计算与反应堆特性分析均有着重要意义[4-6]。

目前主要通过理论计算和实验研究来获取材料接触界面的热阻[7],其中,理论计算采用的模型包括单点接触换热模型[8-9]、基于热载子传递的声学失谐模型[10]、扩散失谐模型[11]、考虑材料粗糙度分布的接触换热模型[12-13]、考虑分形理论的接触换热模型[14]等。由于接触热阻受接触材料热物性参数、机械性能参数、几何形貌、表面状态等众多因素的影响,基于理论模型的数值模拟无法实现对接触热阻的精准预测。因此,工程上通常采用实测方法获取不同设计条件下固体界面的接触热阻。目前,已开展了包括低温[15-16]、高温[17-18]和真空环境[19-20]下各类金属材料的接触热阻实验[21-23]。

ODS MA754合金是一种均匀弥散、具有高热稳定性与化学稳定性的纳米氧化物颗粒高性能镍基合金,其耐高温、抗高温蠕变、抗辐照损伤等性能优异,是空间反应堆系统的重要候选材料[24-25]。将ODS MA754合金作为结构材料开展空间反应堆方案设计时,需要明确该合金材料在不同条件下的接触热阻及其变化特性。因此,本文开展了ODS MA754合金表面接触热阻的实验研究,选择工程上可行且精度较高的稳态法进行界面接触热阻测试,构建了接触热阻测试平台,测量了多影响因素、宽参数范围内ODS钢界面间的接触热阻,给出了接触热阻随温度、压力、环境气体氛围及表面粗糙度等影响因素的变化规律,为基于ODS合金的空间反应堆方案设计提供了数据支撑。

1 实验系统设计与实验原理

1.1 实验系统设计

如图1所示,该实验系统由5个部分组成:试件部分、加热-冷却装置、加压装置、充气装置以及外部箱体。

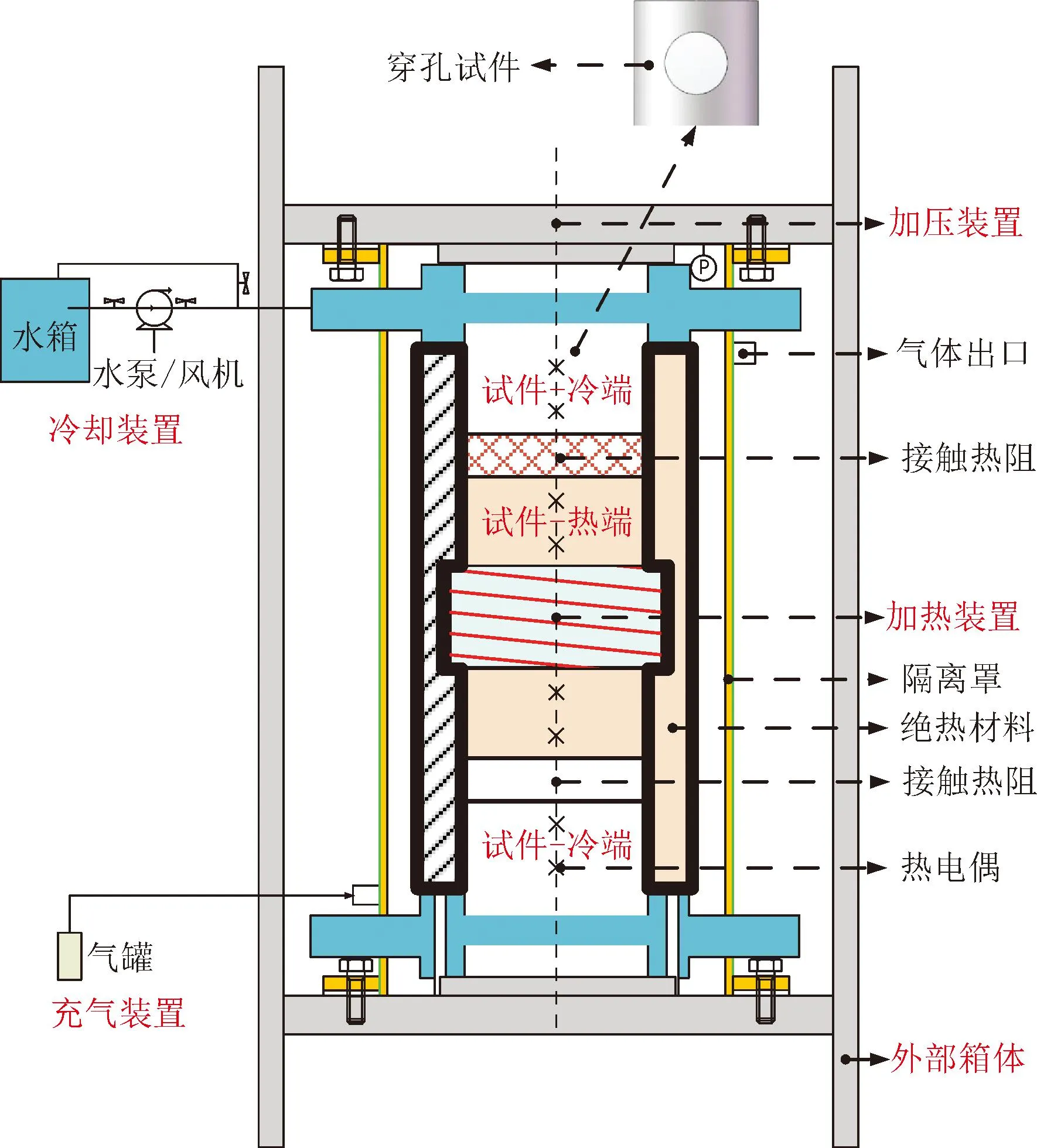
图1 接触热阻实验装置Fig.1 Thermal contact resistance tester

(1)试件部分。试件部分由1段热端试件、2段冷端试件以及试件内部的热电偶组成。3段试件叠放在一起,热端试件位于中部,冷端试件位于两端,整个试件部分形成两个接触界面,接触面的粗糙度分别为1.6、3.2 μm。如图2(a)所示,冷端试件是长为170 mm、直径为30 mm的圆柱体,其和冷却装置相连通的部分有直径为10 mm的圆孔,圆心距离试件顶端15 mm,该圆孔的主要作用为强化试件端部散热。热端试件同样是长为170 mm、直径为30 mm的圆柱,试件正中部是加热区,总长为50 mm,均匀缠绕着加热电阻丝,如图2(b)所示。

(a)冷端试件

(b)热端试件与加热丝

测温热电偶位于试件内部,分别布置在距离热端试件接触面5、15、30 mm和距离冷端试件接触面5、15、45 mm的12个横截面中心处。与此同时,每个横截面半径10 mm处也布置有1个热电偶。图3给出了热电偶孔的分布位置。布置在同一横截面上的两个热电偶主要用于对比确定试件的径向散热,实验中,当径向热电偶温差不超过2℃时,可认为试件的保温效果较好,热量仅沿轴向传递,径向散热可以忽略不计。为了方便热电偶的布置,同一横截面的热电偶不能从同一径向引入,为尽量减小热量沿轴向传递的扰动,热电偶加工孔直径取值为1 mm。

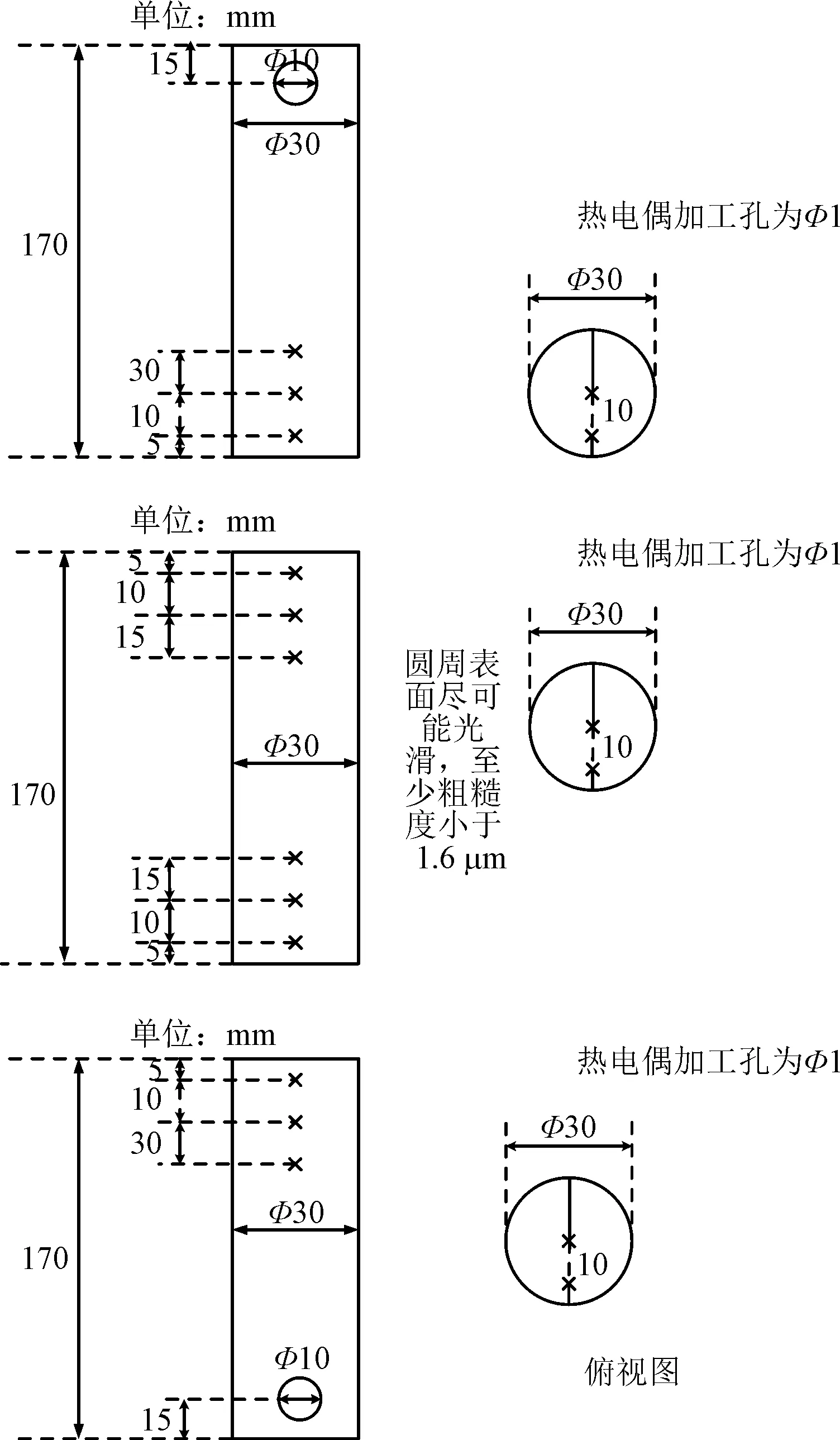
图3 热电偶孔位置分布图Fig.3 Thermocouple hole location distribution

(2)加热-冷却装置。加热-冷却装置主要包括加热部分和冷却部分。加热部分由一个盘管加热器和温控系统组成,加热器为环形,内直径为30 mm,加热丝直径为2 mm,加热环内径与试件被加热段直径相同,以保证两者能完全贴合。加热器产生的热量沿着试件轴向分别向上、向下传递,温控系统可实现加热器功率的调节与显示,并能预设加热器的最高加热温度。加热器的功率变化范围为0～500 W,最小功率变化为0.1 W。冷却部分主要由空压机及矩形冷却管道组成,冷却管道将空压机作为气源,通过阀门改变冷却剂流量从而改变冷却功率,冷却空气流量的变化范围为0～3 240 L/min。加热器和冷却管路相互配合,进而实现改变冷、热两试件接触面温度的功能。

(3)加压装置。加压装置主要由加压部分和控制部分组成。加压部分包括落地门式结构、台面板、移动梁、上横梁、立柱、滚珠丝杠组成的刚性实验框架,采用交流伺服电机作为动力源,通过高效率的圆弧同步带减速系统进行减速,经减速系统驱动滚珠丝杠进行加载。加压装置的主机外形尺寸为2.5 m×2.0 m×0.6 m。控制部分包括高精度负荷传感器与控制系统,当加压装置施加压力于下方试件时,高精度负荷传感器可测得压力值,用该压力值除以接触面积,即得到界面压强。

(4)充气装置。在空间堆方案设计中,为尽可能地降低材料接触表面因未能完全接触导致的传热性能不佳,堆芯通常被包容在含有He或CO2的气氛中,依靠气体导热降低接触界面处的接触热阻。因此,实验测试系统设计有充气装置,并通过管路与实验系统相连。实验开始前,先将气体通入系统,放置全部实验装置于He或CO2气氛中。打开He或CO2的充气罐阀门,等待10分钟待气压平衡后,密封系统并正式开展实验。

(5)外部箱体。外部箱体主要由保温箱体和隔离罩两部分组成。保温箱体分为内、外两层,内层部分为直径211 mm的圆柱型空腔,试件位于中部,其余空间由气凝胶隔热毡填充,并采用珍珠岩粉末填补隔热毡与试件之间的缝隙。外层部分为环形筒体,内部填充气凝胶隔热毡。由于本实验需要置换接触界面间隙的空气为He或CO2,考虑到不易将气凝胶隔热毡的内部空气全部置换干净,可能会导致其向外扩散从而影响接触面间隙的气体氛围,故将气凝胶封装在密封金属容器内,这样做的同时也减少了实验所需置换的气体量。

1.2 实验原理

实验过程为一维稳态传热,根据傅里叶公式

(1)

式中:Q为试件的轴向传热量;λ为试件的热导率;A为实验件的横截面积;Δx为轴向距离;ΔT为Δx对应的温差。实验中,若试件导热系数和轴向几何尺寸已知,则A和Δx已知。

将试件每一横截面上两个径向热电偶所测得的温度取平均值,记作该横截面的温度T。根据热端试件中距离接触界面最近的两个截面(5、15 mm)处的温度差,可求出经过实验热端试件中的传热量Q1。同理,可求出冷端试件中的传热量Q2。根据一维稳定导热原理,应有

Q=Q1=Q2

(2)

实验中,取传热量为通过实验热端和冷端试件传热量的平均值,表示为

(3)

由于实验试件的热导率会随温度发生变化,故需要多次迭代计算得到接触面温度。将热端试件的接触面温度记为T1,取迭代初值为轴向热电偶在距离接触面5 mm截面处的温度,则可确定此段距离的平均热导率;然后根据式(1),求出接触面与轴向热电偶在距离接触面5 mm截面处的温差,由于后者温度已知,则可得到一个新的接触面温度T′1。若T′1和T1的偏差在1%以内,则将T′1计为界面处的温度;若偏差较大,则令T1=T′1,重新迭代直至满足1%的收敛误差。同理可得冷端试件接触面处的温度,记为T′2。

界面接触热阻的表达式可写为

(4)

式中:T′1、T′2分别为热端试件和冷端试件接触面处的温度。

通过式(4),最终可计算出界面接触热阻。

2 实验结果及分析

2.1 接触面温度、压力对接触热阻的影响

在空间堆系统的启动及典型瞬态过程中,反应堆功率和结构材料的热膨胀约束,将会改变材料接触面温度和压力。因此,首先开展了接触面温度和压力对接触热阻的影响研究。

图4、图5分别给出了He、CO2气氛下,温度和压力变化对接触热阻的影响规律。从图中可以看出,界面接触热阻随接触面温度的升高而减小,随接触面压力的增大而减小,且随着接触面温度与压力的进一步增大,减小的幅度逐渐变小。这是由于接触面温度和压力对接触热阻的影响,分别与试件受热后界面接触点的膨胀以及受压后界面接触点的形变有关。接触面温度升高,接触点受热膨胀导致界面间的实际接触面积增大;而接触面压力增加,接触点的弹性或塑性形变也会导致界面间的实际接触面积增大,界面接触面积的增大直接导致了接触热阻减小。然而,随着接触面温度与压力的升高,接触点受热膨胀以及受压变形的程度会越来越小,即实际接触面增大速率会越来越小,从而接触热阻减小的幅度逐渐变小。此外,通过测量试件实验前后接触面的粗糙度,发现试件的表面形貌及接触面粗糙度均无明显变化,因而推断实验过程中接触面发生的是弹性形变,由此排除了温度和压力引起接触面粗糙度变化进而影响接触热阻变化的微观机理。

图4 温度、压力变化对接触热阻的影响(He气氛)Fig.4 The influence of temperature and pressure change of contact surface on thermal contact resistance in He environment

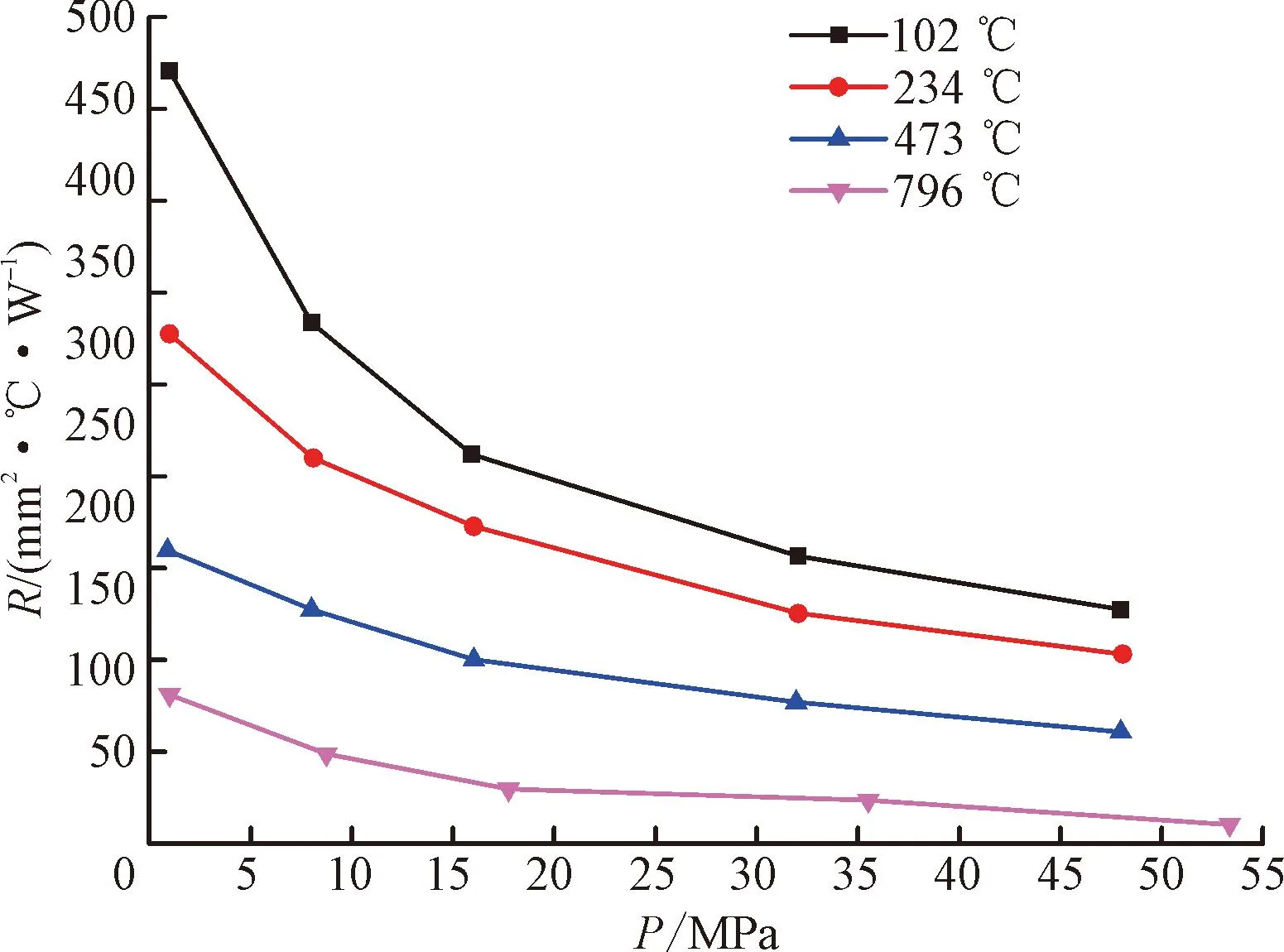
图5 温度、压力变化对接触热阻的影响(CO2气氛)Fig.5 The influence of temperature and pressure change of contact surface on thermal contact resistance in CO2 environment

2.2 接触面粗糙度对接触热阻的影响

随后,开展了接触面粗糙度对接触热阻影响的研究。图6给出了He气氛中,接触面粗糙度对接触热阻的影响规律。可以看出,接触面粗糙度越小,接触热阻就越小。在200、460℃下,接触面粗糙度为1.6 μm时的接触热阻均约为粗糙度3.2 μm时的1/2。这是因为接触面粗糙度越小,接触面的实际接触面积越大,从而导致接触热阻减小。

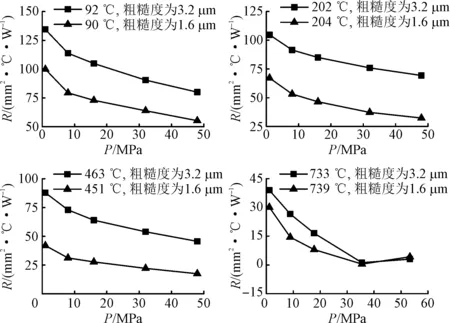
图6 不同温度下接触面粗糙度对接触热阻的影响(He气氛) Fig.6 Effect of contact surface roughness on thermal contact resistance in He environment at different temperatures

对于粗糙度相同的界面,界面波纹形貌可能并不相同。如图7所示,虽然图中两试件的界面粗糙度相同,均为3.2 μm,但左侧试件界面较为光滑(即无明显波纹),而右侧试件界面能看到明显的波纹。这是由于接触面粗糙度的定义为表面轮廓的算术平均偏差(见图8),因此,相同的粗糙度可以有许多种形貌表征[26]。不同的加工工艺,例如刨、车、铣、镗等,以相同的粗糙度对试件进行加工,得到的表面形貌可以完全不同,如图9(a)所示。即使相同的加工工艺,例如磨削,由于刀具的改变也可能会使表面呈现出不同的形貌,如图9(b)所示。图10给出了粗糙度相同但界面波纹形貌不同时,接触热阻随压力的变化规律。可以看出,接触热阻不仅和接触面粗糙度有关,还和接触面粗糙度的表面形貌有关。虽然粗糙度相同,但表面波纹形貌不同时接触热阻也不同。相较于表面有明显波纹的接触面,表面无明显波纹的接触面在同一压力下测得的接触热阻较小,是因为表面无明显波纹的接触面在接触时界面间的接触点更多,从而有着更大的实际接触面积,导致接触热阻较小。

上述仅对波纹形貌的影响进行了定性对比实验,波纹形貌的评价参数以及对接触热阻的定量影响仍需开展深入研究。

图7 同一粗糙度不同表面波纹形貌对比Fig.7 Comparison diagram of different surface ripple morphology with the same roughness

(a)刨、车、铣、镗工艺

(b)磨削工艺

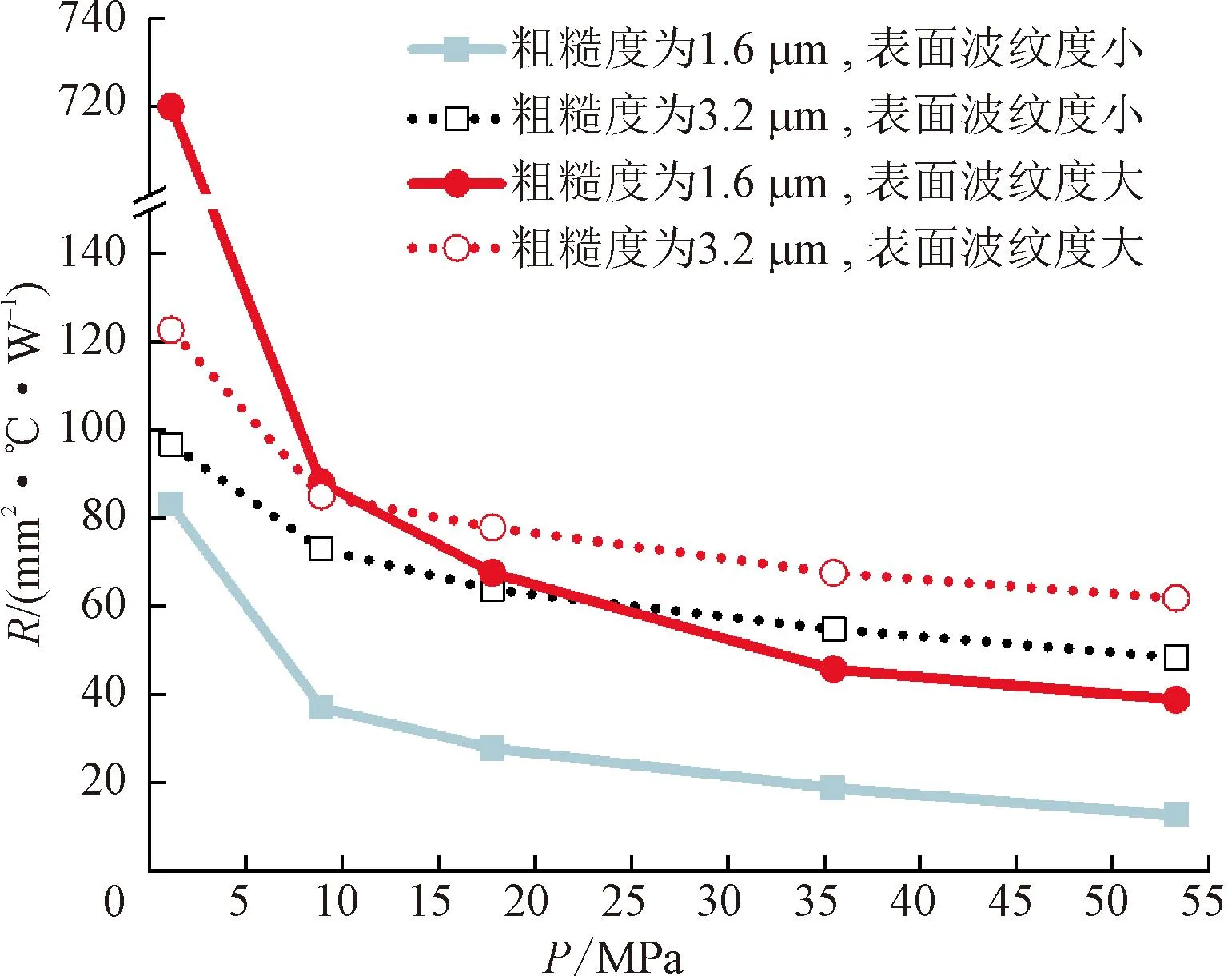
图10 接触热阻随接触面表面波纹形貌的变化 Fig.10 Change of thermal contact resistance with ripple morphology of contact surface

2.3 环境气体氛围对接触热阻的影响

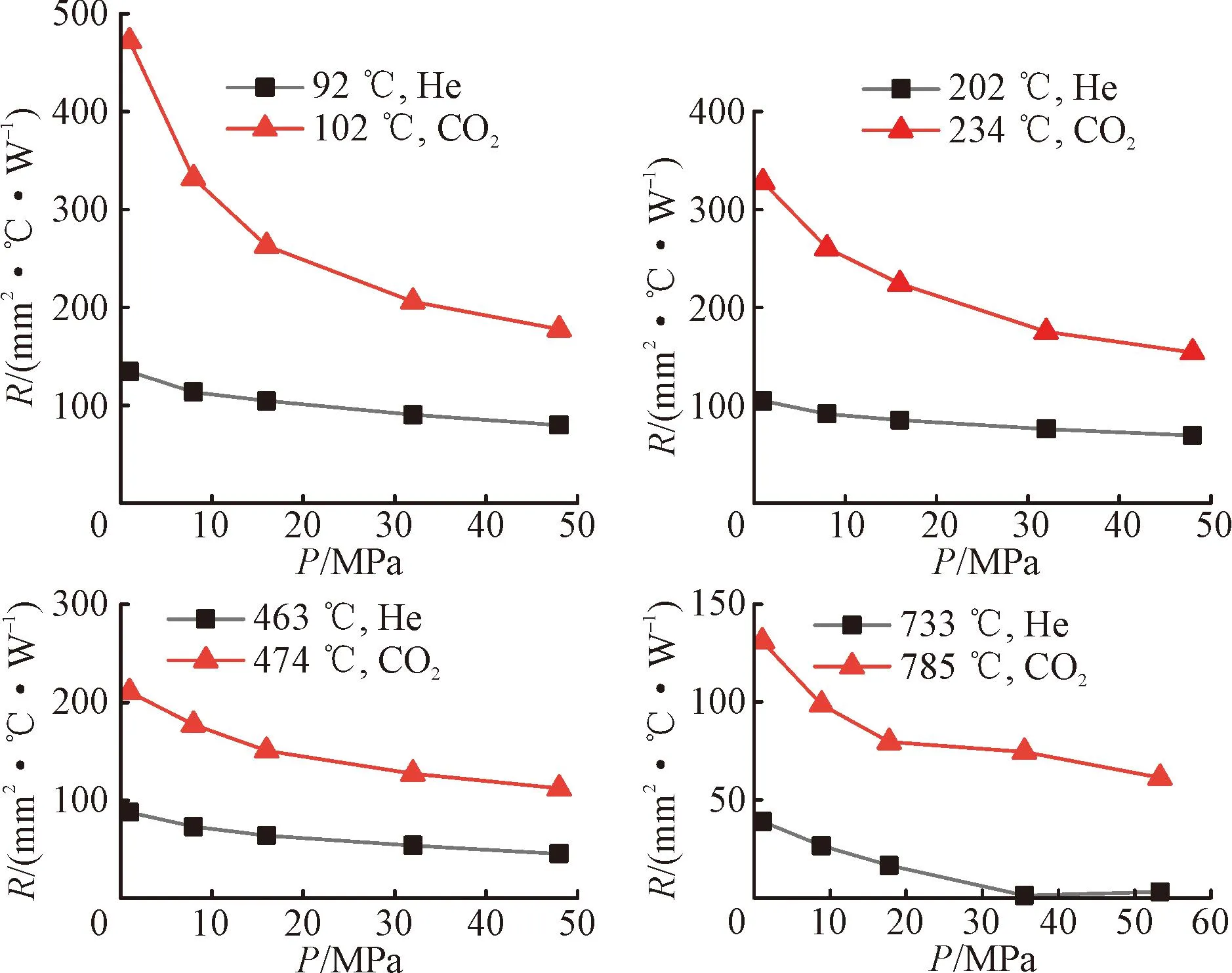
图11 不同温度下接触面环境气氛对接触热阻的影响 Fig.11 Influence of gap gas on thermal contact resistance at different temperatures

图11给出了接触面粗糙度均为3.2 μm时,不同环境气体氛围对接触热阻的影响。由图可见,对于不同气氛,接触面的温度难以控制到完全相同,只能处于相近的温度范围。0.1 MPa压力下,100、220、470℃附近He气氛下的接触热阻约为CO2气氛下接触热阻的1/4、1/3、1/2。不同接触面温度时,He气氛下的界面接触热阻均明显小于CO2气氛下的,这是因为界面接触热阻受界面接触空隙介质的影响,空隙介质不同则热导率不同,而空隙介质的热导率越高,对应介质氛围下的界面接触热阻就越小。0.1 MPa压力下,CO2、He气体的热导率分别为0.0137、0.144 W· (m·℃)-1,两者相差10倍左右,因此在同等实验工况下,He气氛中测得的接触热阻就会明显小于CO2气氛中的。由图还可以看出,随着接触面压力的增加,界面间的实际接触面积增大,导致界面间气体减少,故气体氛围的影响呈现减小的趋势。即便如此,当接触面压力增加到53 MPa时,气体氛围的影响仍占主导地位。

2.4 实验误差分析

影响接触热阻实验精度的因素主要有温度测量和漏热。对于温度测量部分,使用的K型热电偶及数据采集系统精度为1.5℃,使用数采卡连续采集热电偶温度,在温度稳定后选取5 min内采集数据的平均值作为测量值。对于漏热部分,在开展接触热阻实验之前已通过Fluent软件进行了数值模拟,得到不同温度下的加热和冷却功率,如表1所示。

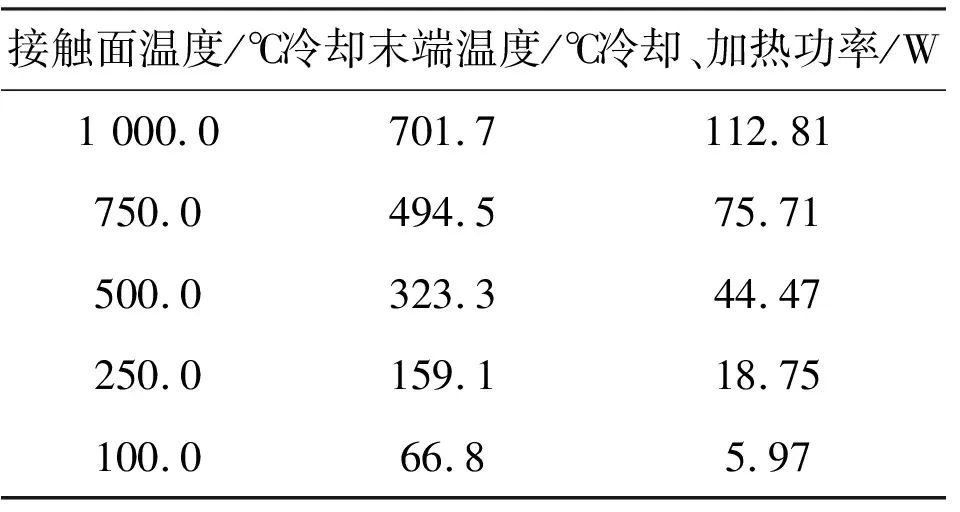
表1 不同温度下试件换热数值模拟结果

本实验中,设计保温箱体内保温棉的厚度为500 mm,保温棉在导热过程中产生的换热量φ1计算如下

(5)

式中:λ为试件的热导率;l为试件的高度;t1和t2为保温棉内、外表面温度;r1和r2为保温棉箱体的内、外半径。

保温棉外表面发生的是对流传热,其换热量φ2可用牛顿冷却公式计算如下

φ2=AmhΔTm

(6)

式中:Am为对流换热面积,即保温棉罩和空气接触的面积;h为对流换热系数;ΔTm为保温棉外表面和空气的温度差。

利用式(5)、式(6),可求出保温棉的温度和散热功率,进而得到漏热率等保温性能参数,如表2所示。可以看出,当保温棉厚度为500 mm时,保温箱体外表面漏热率均在5%以内,因此,可认为此设计保温性能良好,漏热对实验结果影响较小。

表2 不同温度下保温棉的保温性能参数

接触热阻实验数据的不确定度主要由以下两个方面组成:一是热电偶温度测量误差,二是漏热。采用K型热电偶进行温度测量,其温度测量误差可写为

(7)

式中:UΔTc为热电偶热端和冷端温度差的不确定度;ΔTc为热电偶热端和冷端的温度差;UTc为热电偶的测量精度。

通过误差传递公式,可得接触热阻实验系统的误差为

(8)

式中:UR为接触热阻测量不确定度;qloss为漏热功率;q为加热功率。

由式(8),可计算得到不同温度下接触热阻的实验误差,如表3所示。可以看出,本实验采用的热电偶和保温设计,可以保证接触热阻测量总误差在5%以内,具有较高的实验精度。

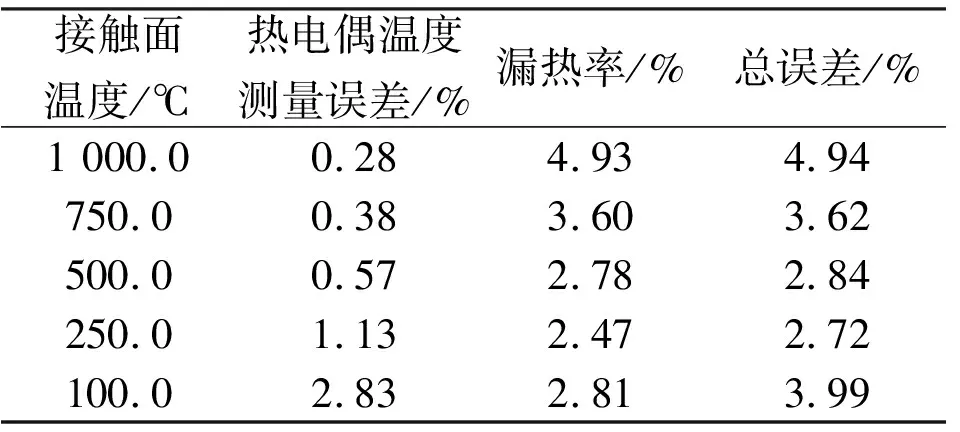
表3 不同温度下接触热阻的实验误差分析

3 接触热阻数据库

接触热阻的大小受很多因素的影响,主要包括接触界面的压力、粗糙度、温度及介质材料等。实验采用基于控制变量的思路,获得了对应于影响因素离散变量的接触热阻值。由于过多地增加离散变量点会增加实验成本,因此,解决该问题的有效办法之一就是基于合理的离散变量和对应接触热阻值,采用先进的插值算法进行结果预估。与最近点赋值法、线性插值法、立方插值法等相比,本文所采用的双谐波样条插值法能够在保持曲线平滑的同时,尽可能地接近给定的数据点。因此,本研究采用该实验系统开展了更宽温度(20～800℃)与压力(0～80 MPa)范围的ODS MA754合金接触热阻测量实验,获得了约200组数据点,如图12、图13 所示。

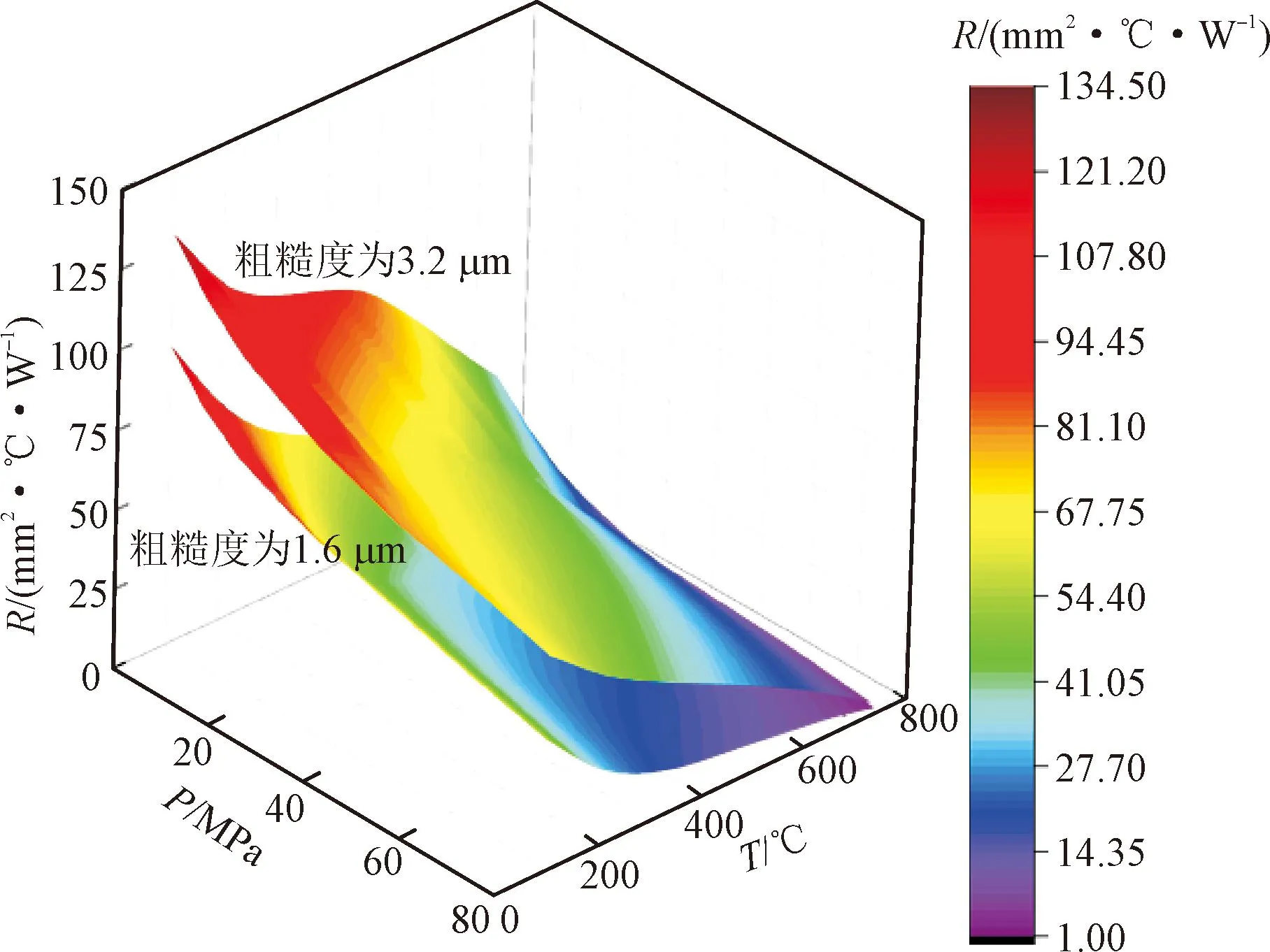
图12 接触热阻随温度和压力的变化(He气氛) Fig.12 The variation of thermal contact resistance with temperature and pressure (in He environment)

基于实验获得的宽量程接触热阻数据点,建立了ODS MA754合金接触热阻数据库及查询系统,实现了对多影响参数下材料接触热阻的快速查询。同时采用图形分析,获得了接触热阻和影响因素之间的关系及变化趋势,得到了不同工况下接触热阻的数据拟合值。开发的数据库界面如图14所示。

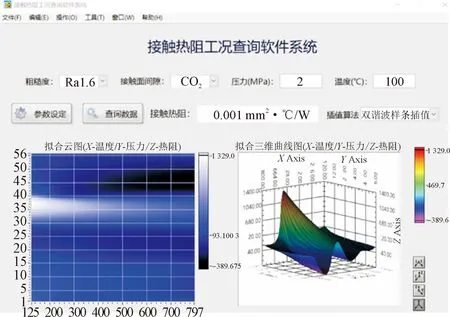
图14 接触热阻数据库界面Fig.14 Thermal contact resistance database interface

4 结 论

本文通过自主研发设计的高温、高压接触热阻测量装置,在气体氛围分别为CO2、He时,针对ODS MA754合金材料试件开展了1.6、3.2 μm两种典型表面粗糙度、温度范围为20～800℃、压力范围为0～80 MPa的接触热阻测试,研究了各因素对接触热阻的影响,建立了不同工况下各影响因素与接触热阻之间的定量关系式,并基于实验获得的宽量程接触热阻数据,开发了界面接触热阻数据库,得到如下主要结论。

(1)在温度为20～800℃、压力为0～80 MPa的范围内,随着接触面温度和压力的升高,界面接触热阻降低,且热阻降低的速率逐渐减小。

(2)与表面粗糙度为1.6 μm的试件相比,粗糙度为3.2 μm的试件表面有着更大的界面接触热阻,实验得到的定量关系可为工程样件的加工粗糙度提供参考。

(3)对接触面间隙气体的研究表明,He气氛下接触热阻远小于CO2气氛,0.1 MPa常压下,100℃附近的He气氛接触热阻约为CO2气氛的1/4。

(4)开发的界面接触热阻数据库可实现不同条件下ODS MA754合金接触热阻的快速查询,直接得到相关因素对界面接触热阻的影响规律。