利用长短期记忆神经网络的改进POD-Galerkin降阶模型及其在流场预测中的应用

张译文,王志恒,邱睿贤,席光

(西安交通大学能源与动力工程学院,710049,西安)

由Navier-Stokes (N-S)方程所描述的流体流动具有非线性和多尺度特征,其固有的复杂性使得预测流体流动十分困难。计算流体动力学 (computational fluid dynamics,CFD) 方法可以通过基于偏微分方程的全阶模型 (full order model,FOM) 提供对流体流动的准确预测,但是计算量可能较大,无法做到实时预测。因此,构建低成本流场降阶模型 (reduced order model,ROM) 有很高的应用潜力[1]。流场降阶模型是指从CFD 或实验得到的数据集而构建的低维数学模型,可以预测流场参数。与基于CFD 的分析相比,ROM 可以在很短的时间内准确预测线性和非线性空气动力学过程,速度能够加快1～2个数量级[2],因而在流场快速预测与实时控制中具有重要的应用价值。

根据是否将流动控制方程加入至模型,降阶模型可分为侵入式降阶模型和非侵入式降阶模型两类。侵入式降阶模型将本征正交分解(proper orthogonal decomposition,POD)得到的正交基通过伽辽金(Galerkin)投影的方式投影至流动控制方程上,以此得到由模态时间系数构建的低维模型,因此也称为Galerkin投影式降阶模型[3]。由于考虑了控制方程,侵入式降阶模型能够对N-S方程中各物理项进行解释,进而定量分析出各项的作用大小。近年来,对POD-Galerkin降阶模型有较多应用研究。康伟等[4]提出了一种利用POD的非线性Galerkin方法,用于复杂流体动力系统的低维建模,并以雷诺数为200、攻角为20°时的NACA0012翼型绕流流动问题为例进行了低维建模分析。Aubry等[5]对湍流边界层过渡流动进行了建模,结果表明降阶模型捕捉到了实验观察到的流向涡对运动形态。Deane等[6]重构了周期性凹槽通道中的流动和孤立圆柱体的尾流,研究了模型的短期和长期精度,并对构建降阶模型所用工况之外的工况点进行了测试,结果表明周期性凹槽中流动降阶模型在Re附近能够进行合理的外推。Noack等[7-8]对 Galerkin 模型进行了改进,引入了一种移位模态,使得POD-Galerkin降阶模型能够重构瞬态动力学过程,并以3阶动力学系统重构了Re=100的孤立圆柱绕流。张鸿志等[9]以AGARD 445.6机翼为对象,研究了ROM建立过程中不同参数对于模型精度的影响,并将ROM应用于颤振边界的预测。李静等[10]以低雷诺数下圆柱绕流为对象,构建失稳初期的流动ROM,该模型可以复现流场发散初期的发生趋势。冯俞楷[11]和梁钰[12]对非稳态导热问题构建ROM,给出了涡轮叶片瞬态非线性热传导问题的求解结果,该模型大大提高了计算速度,实现了快速预测。非侵入式降阶模型又称为数据驱动式降阶模型,它不需要给出明确的控制方程,直接从流场的高维流动数据中构建。非侵入式降阶模型可以通过输入、输出量直接建立线性或非线性黑盒模型[13],也可以通过对流场测量数据建立简化流动模型,如代理模型[14]、人工神经网络[15]、非线性系统辨识[16]等。非侵入式降阶模型凭借其模块化的优势[17],在流场降阶模型研究中越来越受到研究者们的关注。Duraisamy等[18]、Saeed等[19]和Reddy等[20]使用机器学习方法提高CFD模拟的准确性,以神经网络来预测流场不同流动条件和几何形状下的速度和压力场,相较于CFD能够更快地估计流场变化情况。

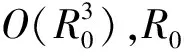
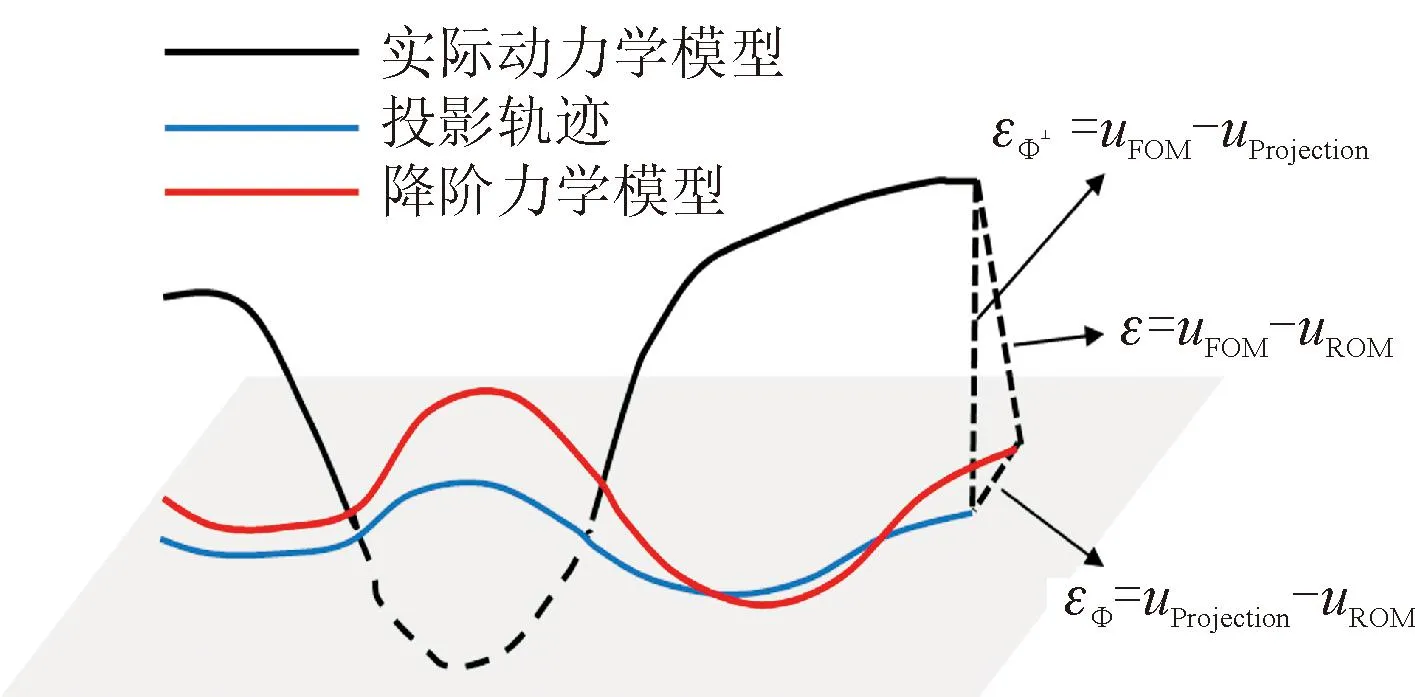
图1 降阶模型中误差来源Fig.1 Error sources in reduced order models

针对上述POD-Galerkin降阶模型存在的误差,通过对模型进行修正,添加额外的作用项使得降阶模型预测轨迹与实际轨迹相符,是切实可行的方法[24-25]。鉴于机器学习方法在提取特征方面的优势,其与流场降阶方法结合有更大的潜力。基于此,本文提出一种引入长短期记忆神经网络(long short-term memory,LSTM)[26]的改进POD-Galerkin降阶模型。该模型通过Galerkin投影来提高降阶模型的可解释性,并通过两个不同的长短期记忆神经网络分别进行大尺度模态的误差修正和小尺度模态的阶数扩展。将改进的POD-Galerkin降阶模型应用于典型的二维圆柱绕流问题的流动预测,通过与标准POD-Galerkin降阶模型的对比,以验证改进降阶模型的有效性和可靠性。

1 引入神经网络的改进POD-Galerkin降阶模型

1.1 POD-Galerkin降阶模型

POD-Galerkin降阶模型可将高阶的偏微分方程组转化为低阶的常微分方程组,其在流场降阶中应用的基本思路是:将数值模拟或实验得到的流场参数作为样本数据,采用 POD方法[27]得到描述流场的一组最佳正交模态,并对低能量模态进行截断,然后将 N-S 方程投影到主要模态上,得到关于模态系数的一组常微分方程组,从而将高阶问题转化为低阶非线性动力学问题。具体建模过程如下。

对于流场数据U(x,t),将每个时刻的流场构成一列数据,选取样本库中N个时刻的数据作为样本,构建流场快照矩阵

(1)

(2)

式中:ai为第i阶POD模态时间系数。

对于不可压N-S方程,在截取的前阶特征模态上作Galerkin投影。投影通过N-S方程与POD模态内积得到,表示为

(3)

式中:u为速度矢量;p为压力;ν为运动黏度;(,)为内积运算符。由此可得m个常微分方程构成的常微分方程组

(4)

式中:Ak、Bk、Ck均为常数项,可以由速度场、速度场梯度项、压力场、压力场梯度项的组合求得。由格林定理和无散度的性质可知,在出口边界p=0的情况下,压力项可以消去。通过求解上述常微分方程组,即可获得各阶模态时间系数的变化趋势,与POD空间模态结合,可以重构原始流场。

1.2 神经网络的引入

针对标准POD-Galerkin降阶模型存在的两个主要误差来源,可以分别添加神经网络项来提高降阶模型的精度。对于第一个误差来源,对流场进行POD后,对高阶模态进行截断忽略了高阶模态在流场中的耗散作用,保留的低阶模态失去了与高阶模态的耦合项,使得耗散误差不断累积,会影响构建的动力系统的长期稳定性。因此,可以通过POD分解得到的时间系数与构建的降阶动力学系统误差引入长短期记忆神经网络[28],建立输入-输出关系,以此修正降阶模型与实际预测值之间的偏差。

定义实际的动力学系统模型

(5)

从实际动力学系统中可以求得变量ak随时间变化的离散值ak(t1),ak(t2),…,ak(tn)等。

假设降阶动力学系统模型为

(6)

对此动力学模型,通过求解线性微分方程组可以得到下一时刻的时间系数

(7)

(8) 式中:ck为降阶模型预测值和真实投影之间的误差。为修正此误差,可以利用LSTM架构来学习矫正项,在每个时间步内,LSTM神经网络将模态系数从降阶模型的预测值引导至真实值上。

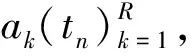
(9)

(10)

综上所述可知,整个神经网络修正过程包括两个阶段,首先通过第一个LSTM神经网络映射来减小第一部分误差,然后通过第二个LSTM神经网络扩展模态阶数来减小第二部分误差。引入神经网络的改进POD-Galerkin降阶模型的计算流程如图2所示。

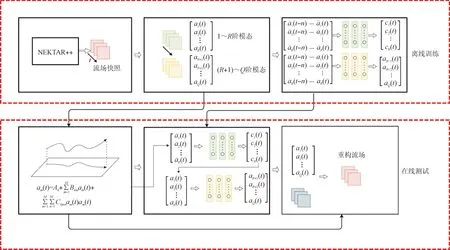
图2 改进POD-Galerkin降阶模型流程Fig.2 Flowchart of improved POD-Galerkin reduced order model

离线训练期间,模型在不同时间节点获得真实的流场信息,进而可以计算得到真实的POD模态时间系数。首先通过标准POD-Galerkin降阶模型逐步计算每个时间步长的模态系数,然后计算f和g两个LSTM项。

在线测试期间,首先从时间零点开始,将当前时刻的流场快照投影到前R阶模态上获得初始时刻的模态时间系数,然后通过标准POD-Galerkin降阶模型进行第一个时间步长的计算。得到第一个时间步长上的模态时间系数后,通过LSTM修正项f计算得到预期的误差ck,再进行第一次的修正,随后通过LSTM扩展项g计算得到扩展模态时间系数,利用两个部分得到的模态时间系数以及保留的前Q阶静态空间流场模态,即可得到高精度的预测流场。

2 改进POD-Galerkin降阶模型的应用

将提出的引入神经网络修正的改进POD-Galerkin降阶模型应用于典型二维圆柱绕流问题的流场预测。研究对象为Re=100条件下圆柱绕流,其来流马赫数较小(Ma<0.1),可以视作不可压缩流动,且传热较小可以忽略,因此在进行数值模拟时仅考虑质量守恒方程和动量方程

(11)

(12)

本文利用 NEKTAR++软件对圆柱绕流进行直接数值模拟,利用 hp 型谱元法直接对流场控制方程组进行求解,求解方法采用经典伽辽金公式与谱元离散相结合的高阶有限元方法,对每个网格单元内部的节点值通过 Gauss-Lobatto-Legendre多项式的拉格朗日展开来近似。

圆柱绕流的计算区域如图3所示。将圆柱直径D作为无量纲处理的特征长度,取D=1,圆柱圆心位于原点,入口和出口边界位于x=-10D和x=20D处,垂直于流向方向长度为-10D～10D。进口速度采用无穷远来流速度进行无量纲处理。

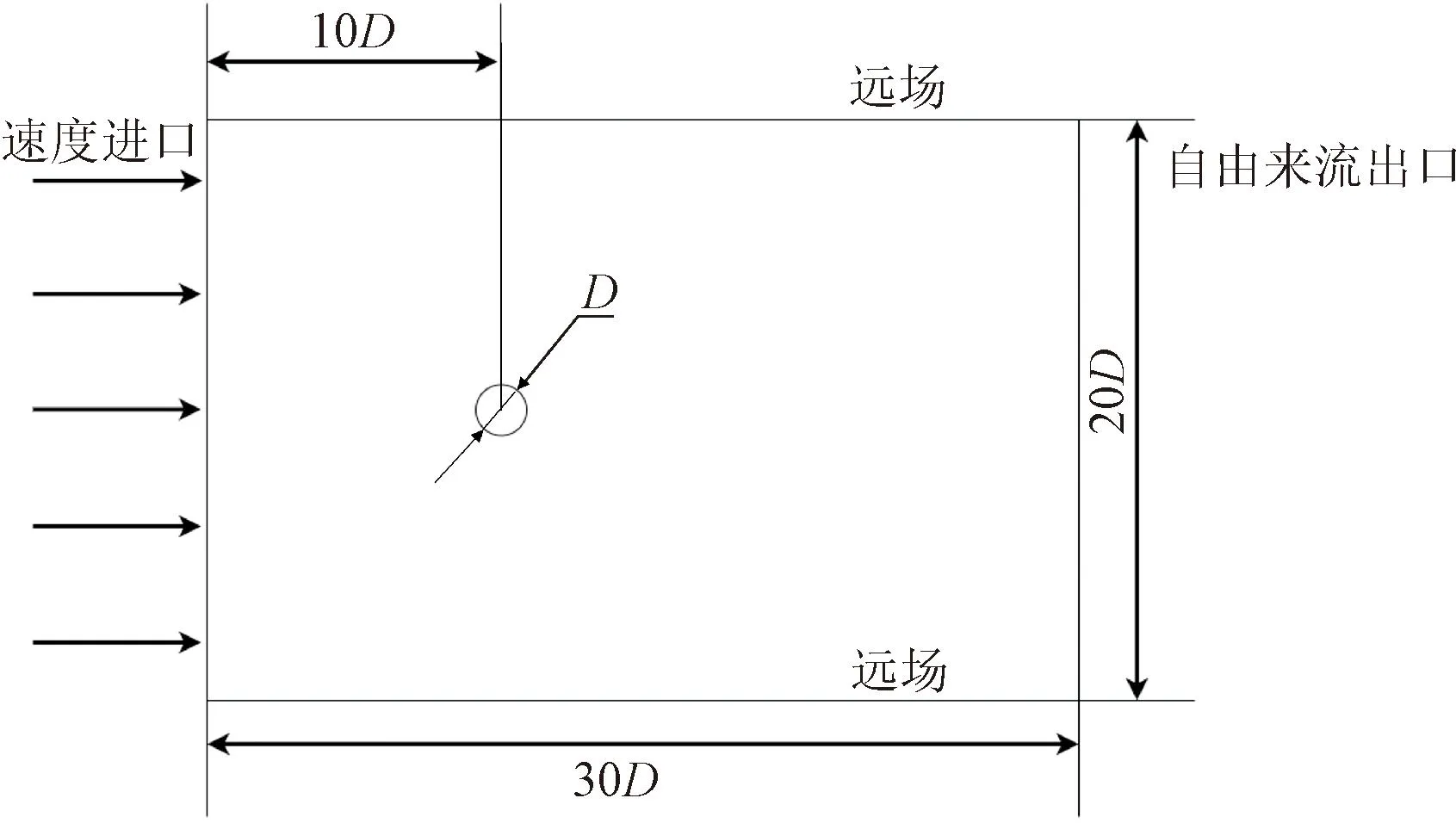
图3 圆柱绕流计算域Fig.3 Computational domain of flow around a cylinder

圆柱绕流的流场网格如图4所示,进口采用均匀速度进口,出口采用自由流出口,用以消除尾迹的影响,圆柱壁面采用无滑移边界。上下边界采用对称边界,以避免壁面对圆柱的影响。在圆柱附近进行网格加密处理,最终的网格节点总数为31 360。

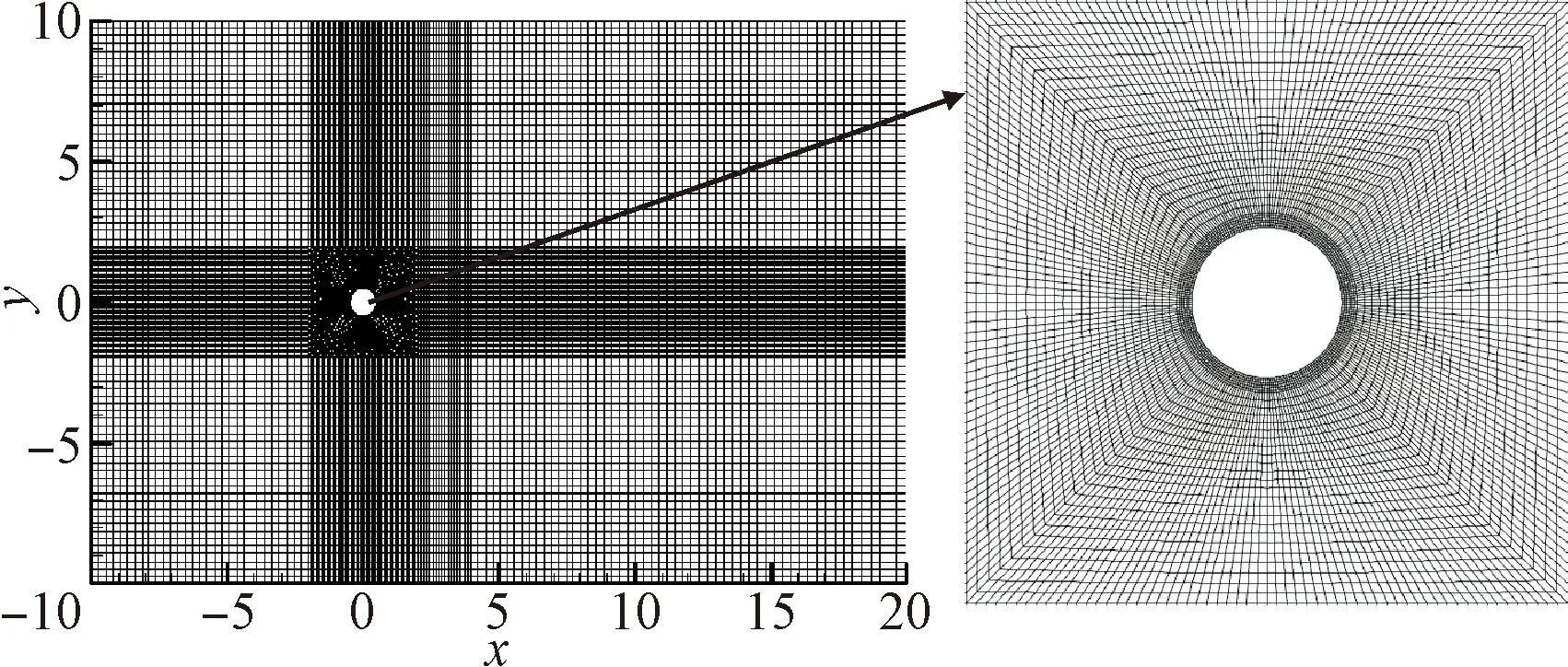
图4 圆柱绕流的流场网格划分及局部加密图 Fig.4 Computational mesh and grid refinement near the cylinder surface

根据边界条件进行非定常计算,待尾迹稳定振荡后采样20个周期的流场数据。定义升力系数Cl、阻力系数Cd及斯特劳哈尔数St为

(13)

(14)

(15)

式中:Fl为圆柱所受到的升力;Fd为圆柱所受到的阻力;ρ为流体密度;Uinlet为进口速度。

将本文数值模拟得到的Cl、Cd及St与文献数据进行对比,结果如表1所示。可以看出,本文数值模拟结果与文献结果吻合较好,本文所采用的数值方法的准确性得到了验证。

表1 升、阻力系数及St与文献数据对比

3 结果与讨论

对周期性流场中1 000个流场快照进行POD,并分别构建4、6、8阶流场降阶模型。不同阶数下的预测前两阶POD模态时间系数(a1、a2)及预测系数a1与POD的绝对误差如图5所示。

(a)a1

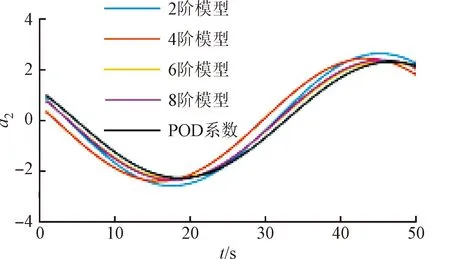
(b)a2

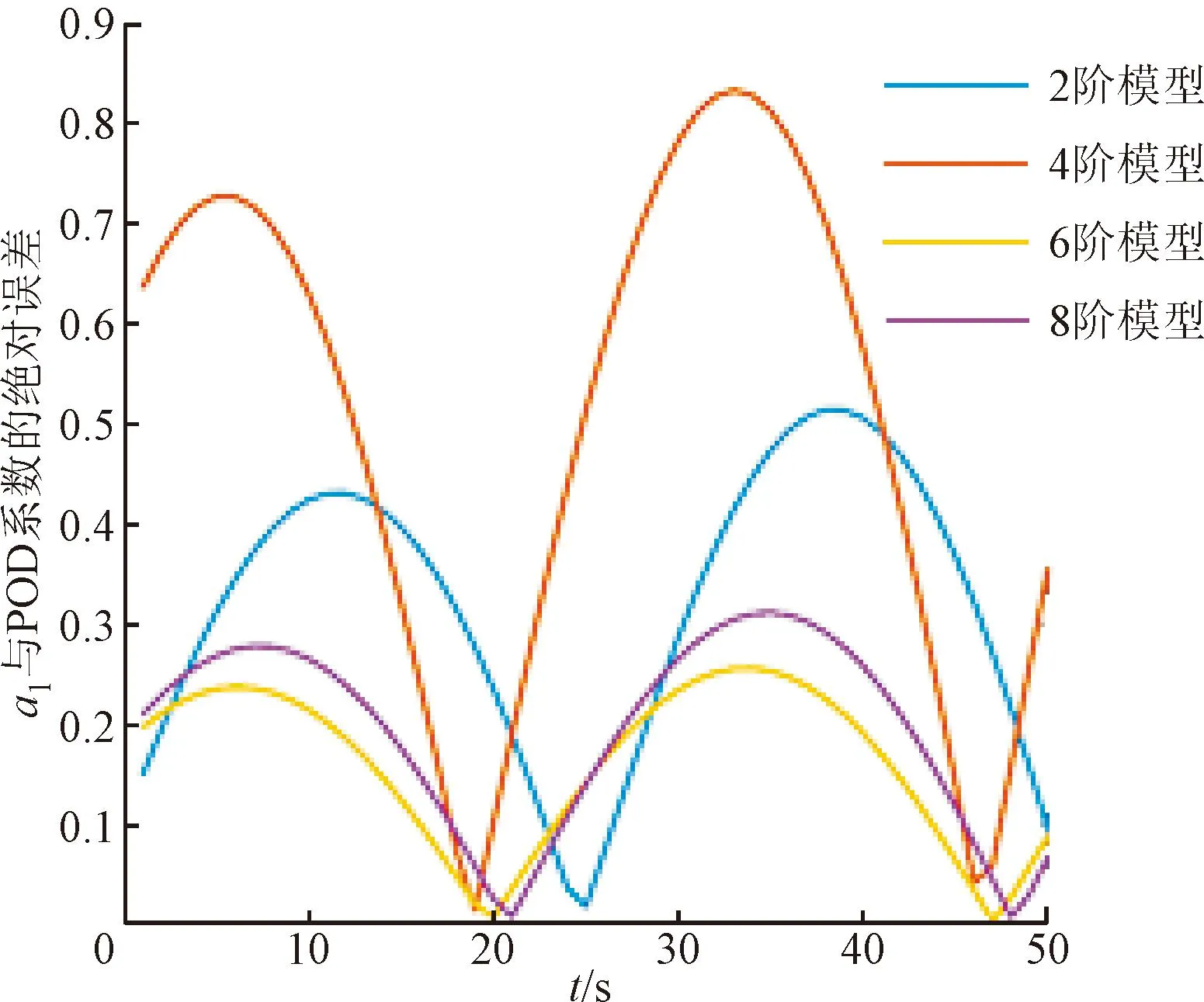
(c)a1与POD的绝对误差

从图5可以看出,起初随着阶数增大,各阶模态时间系数的预测精度逐渐提高。但是,提高至8阶后,误差反而有所增大。这是由于构建的动力学系统中,微分方程中多项式系数由模态投影得到。由于对空间进行离散,数值误差随着多项式系数矩阵大小不断增加,数值误差积累超过了提高阶数带来的改进,因此不断提高降阶模型的阶数并不能使得精度一直增大。此外,对比误差随时间变化的趋势可以看出,对于2、4阶的降阶模型,模态时间系数随时间逐渐增大,有无限发散的趋势,且由于预测周期与实际周期有差别,导致相位误差逐渐累积。对于6、8阶的降阶模型,模态时间系数没有逐渐增大,但是相位误差同样在不断累计,这都导致了误差随时间不断增大。

分别以2、4、6、8阶模型为基准,对POD模态时间系数进行修正,LSTM神经网络的参数如表2所示。

表2 LSTM超参数列表

将训练好的模型添加到POD-Galerkin降阶模型当中,重新进行模态时间系数的计算,即可得到通过神经网络修正的降阶模型数据。图6～9展示了4个不同修正模型和原始POD-Galerkin降阶模型的前两阶POD模态时间系数的对比情况。可以看出,通过神经网络修正后,降阶模型预测的模态时间系数基本与实际值一致,误差也没有逐渐增大的趋势。图8中,第5阶模态相较其他各阶模态误差较大。这是由于给定神经网络训练的均方根误差目标是使得各阶模态的误差之和最小,第5阶模态的修正项并未收敛到局部最优的修正参数。

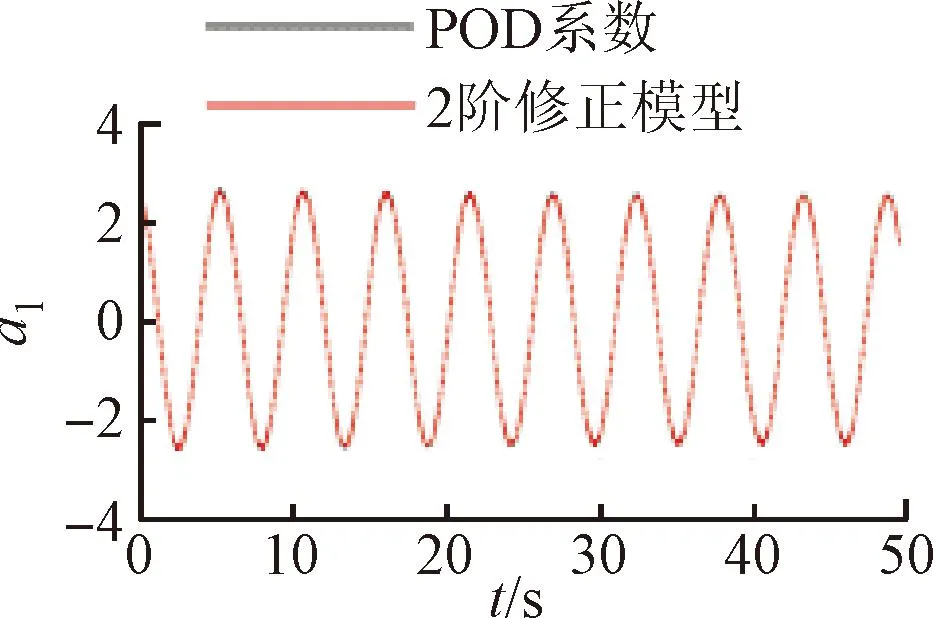
(a)a1

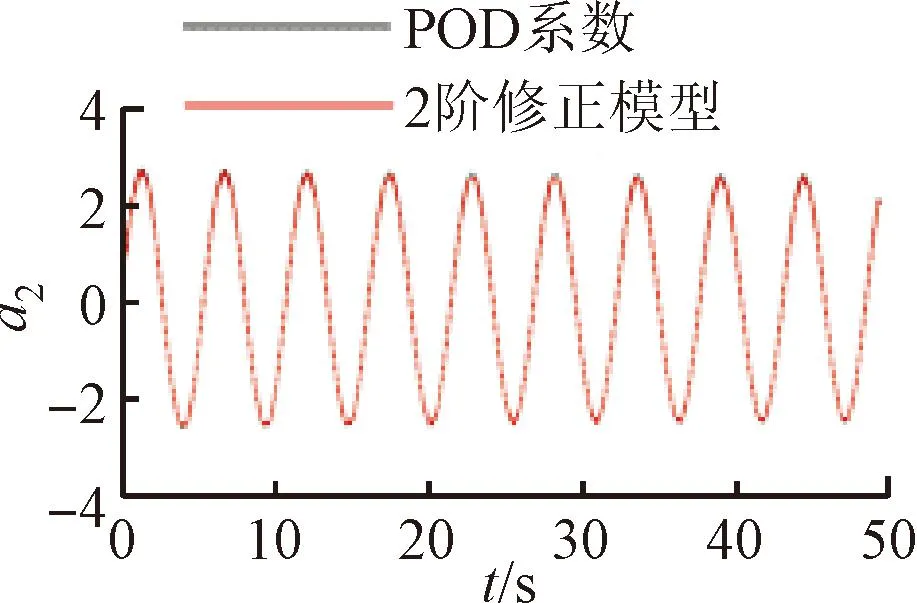
(b)a2

(a)a1

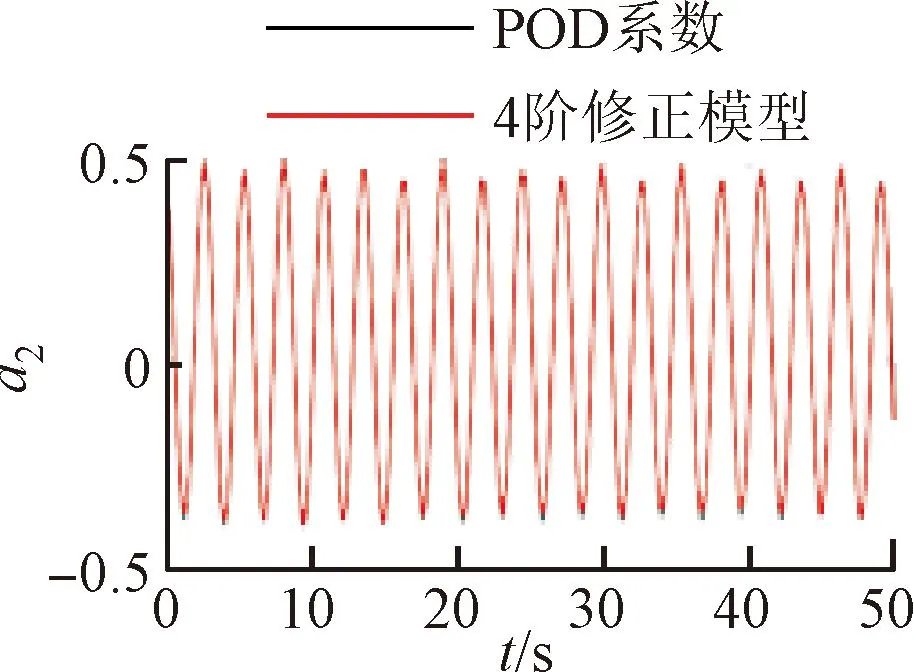
(b)a2

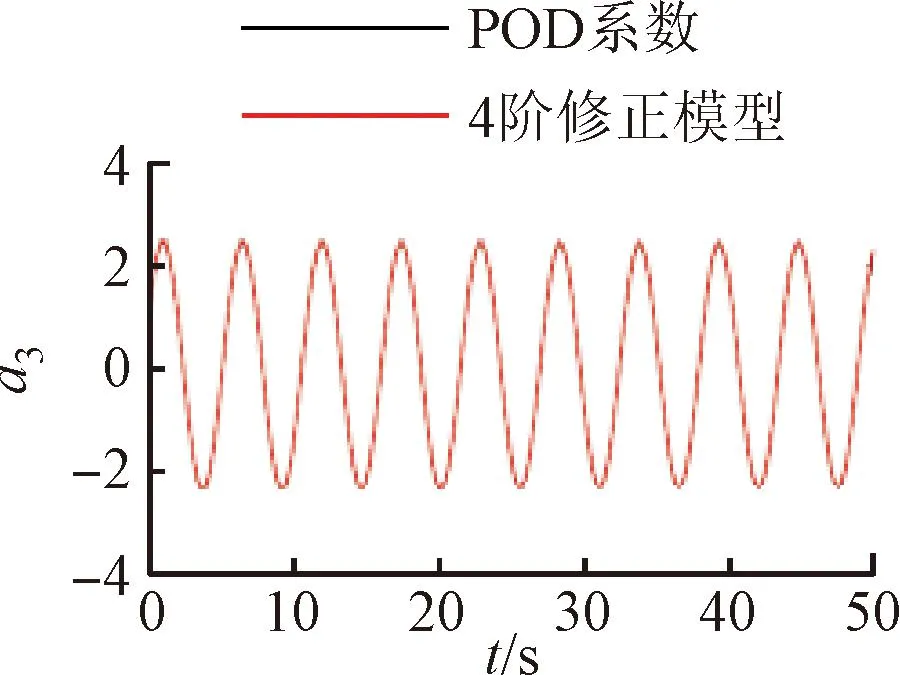
(c)a3

(d)a4

(a)a1

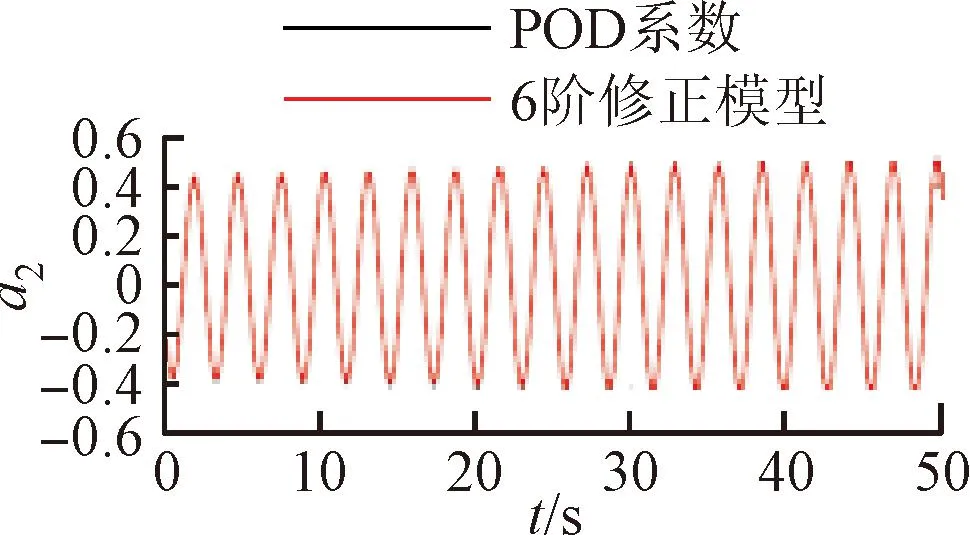
(b)a2

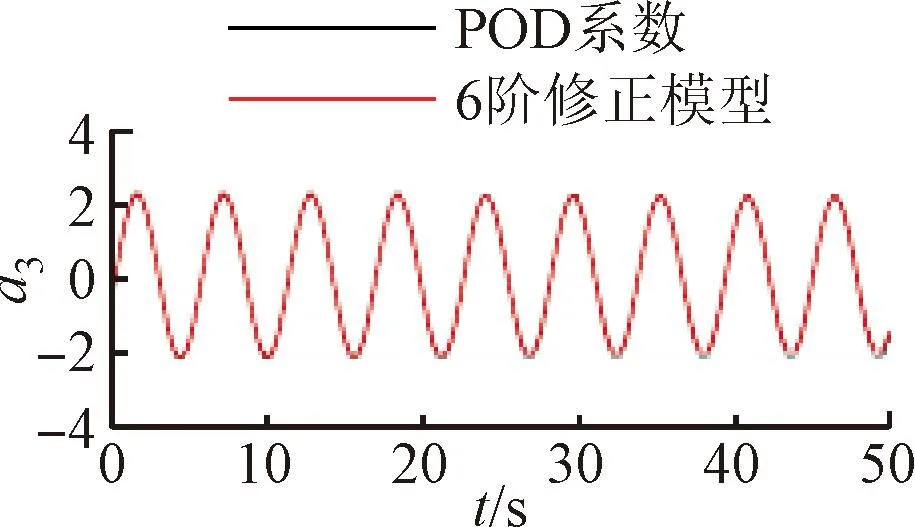
(c)a3

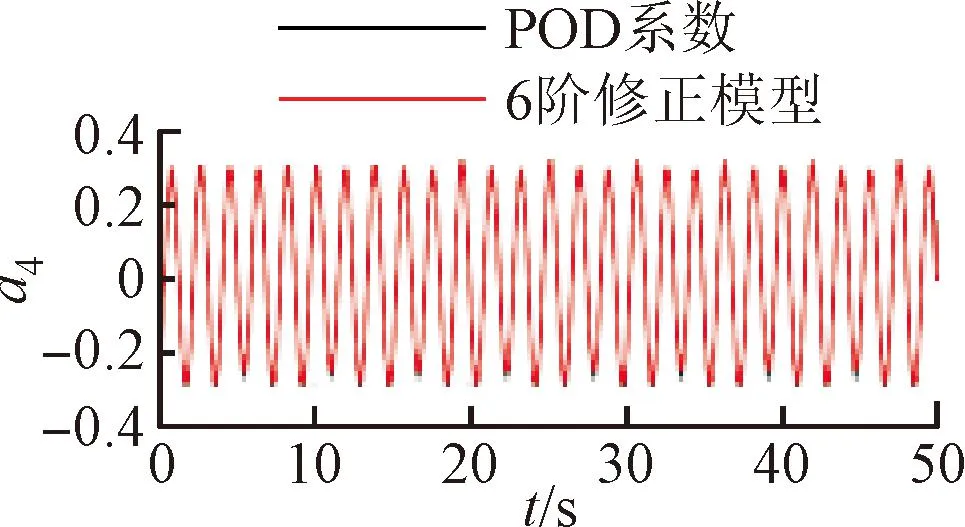
(d)a4

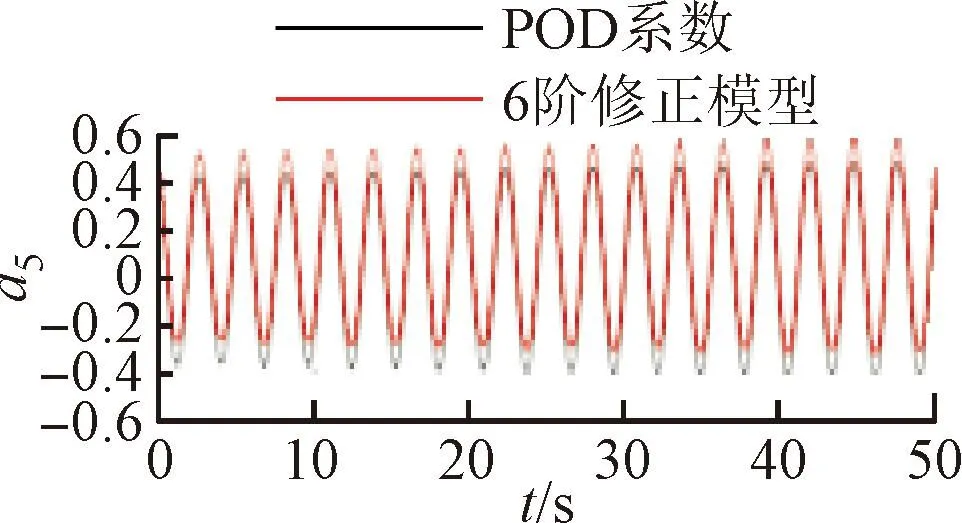
(e)a5

(f)a6

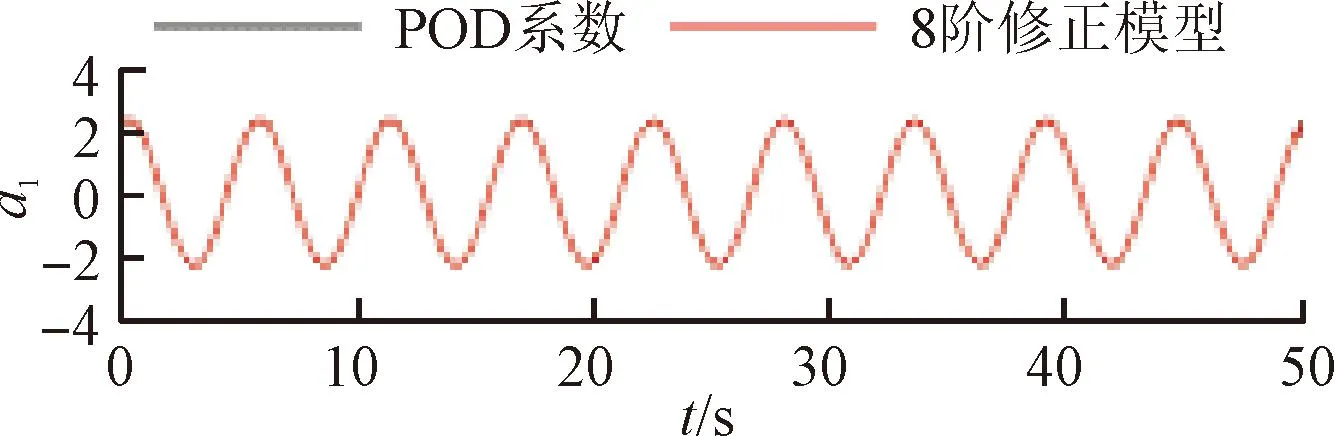
(a)a1

(b)a2

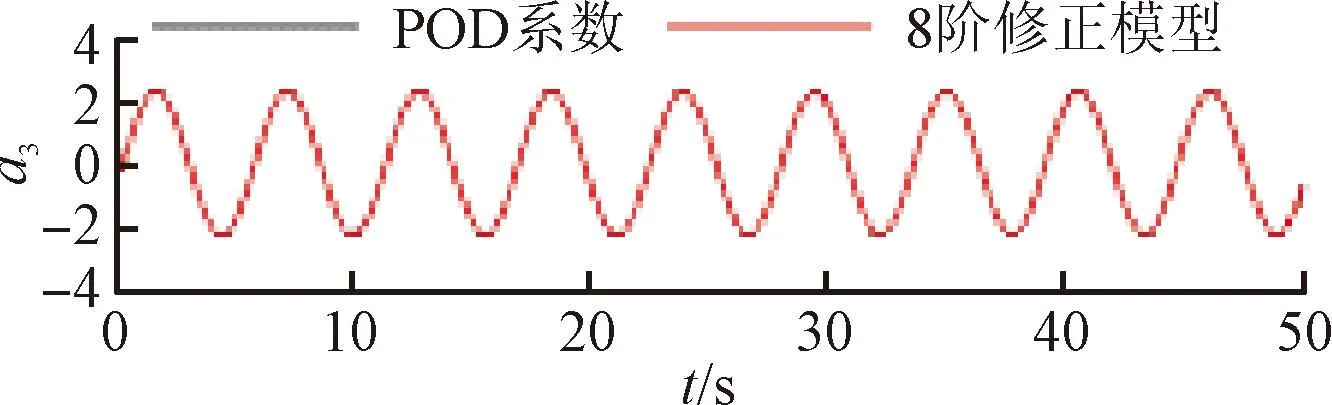
(c)a3

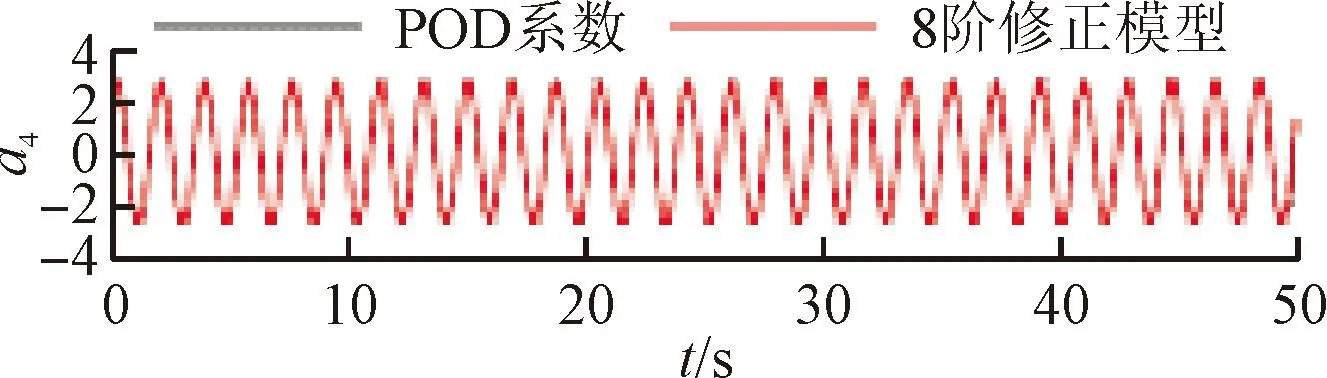
(d)a4

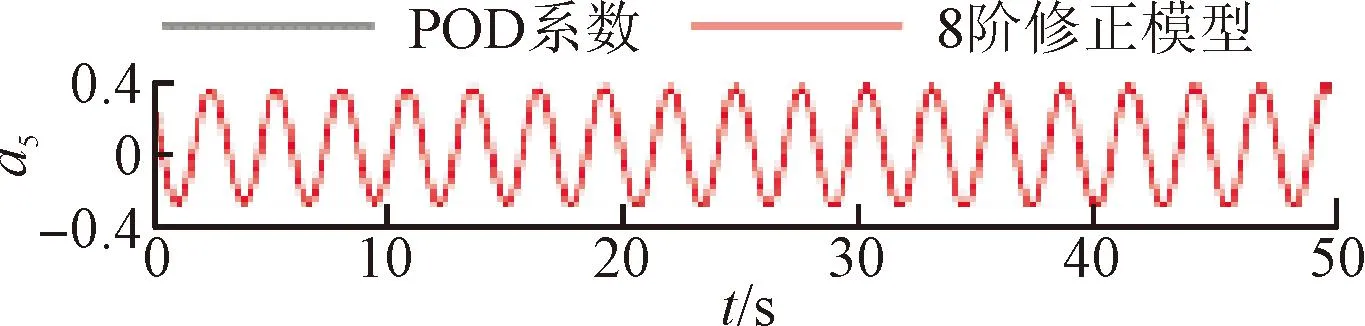
(e)a5

(f)a6

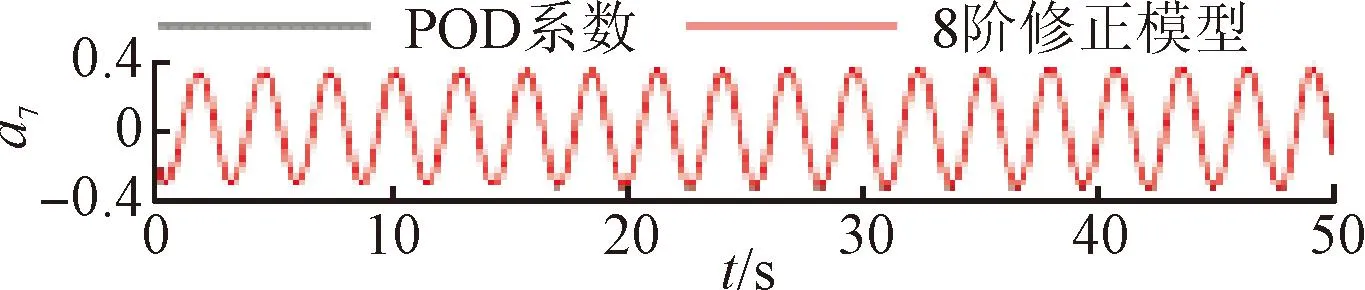
(g)a7

(h)a8

对通过神经网络修正后的降阶模型进行扩展,将2、4、6阶降阶模型分别扩展至8阶。将预测的高阶模态时间系数加入流场重构当中,不同扩展阶数的改进降阶模型预测流场与原始流场的涡量(经过无量纲化处理)对比如图 10所示。可以看出,将2阶模态扩展至8阶,预测流场误差较大,而4阶模态扩展与6阶模态扩展至8阶几乎没有差别,得到的预测流场与原始流场基本一致。

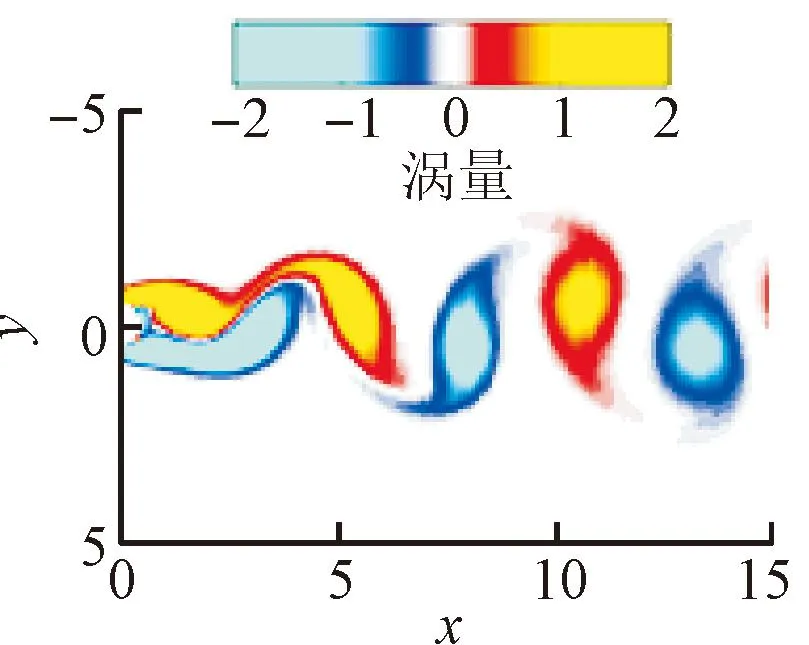
(a)原始流场

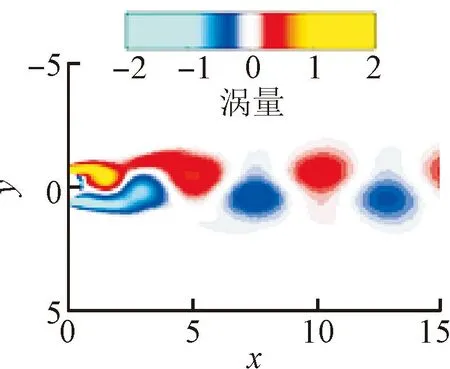
(b)2阶扩展

(c)4阶扩展

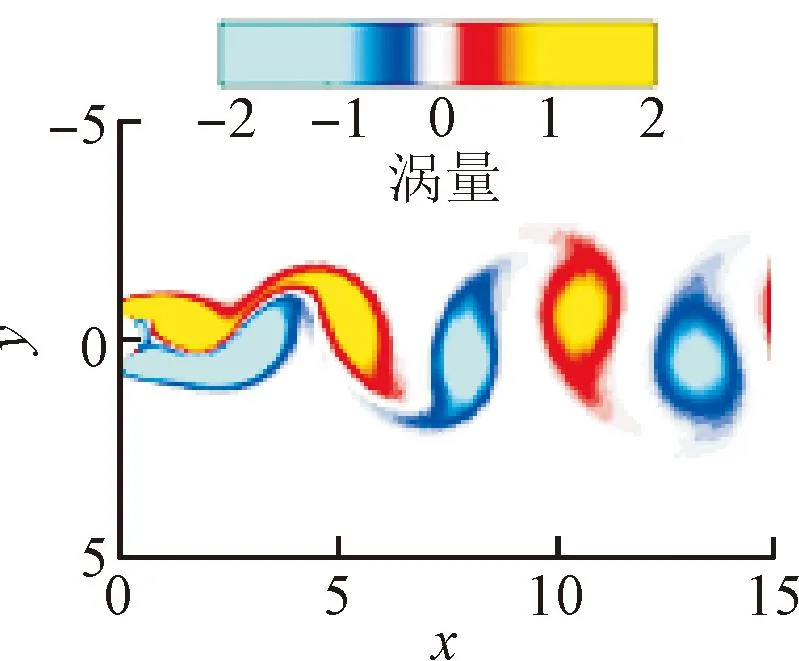
(d)6阶扩展

定义各阶模态时间系数的均方根误差为

(16)

各阶模态时间系数均方根误差如表3所示。各阶模态的时间系数预测与原始数据相比,POD-Galerkin降阶模型在前6阶模态的预测精度较高,而第7阶模态的时间系数有较大的相位误差。改进后模型各阶模态的均方根误差均较POD-Galerkin降阶模型要小1～2个数量级。相较于引入修正项的神经网络,引入扩展项的神经网络预测效果较差,但随着阶数的增大,引入扩展项神经网络模型的预测精度逐渐提高。

表3 各阶模态时间系数均方根误差

表4展示了不同降阶模型计算迭代一个时间步耗费的时间。可以看出,标准POD-Galerkin降阶模型的计算时间随模态阶数的增大而显著增大。由于改进模型已经在训练阶段构建完成,所以添加不同的改进模型带来的时间增长近乎一致。4阶和6阶改进降阶模型相较于原始8阶POD-Galerkin模型速度分别提高了约56%和25%。

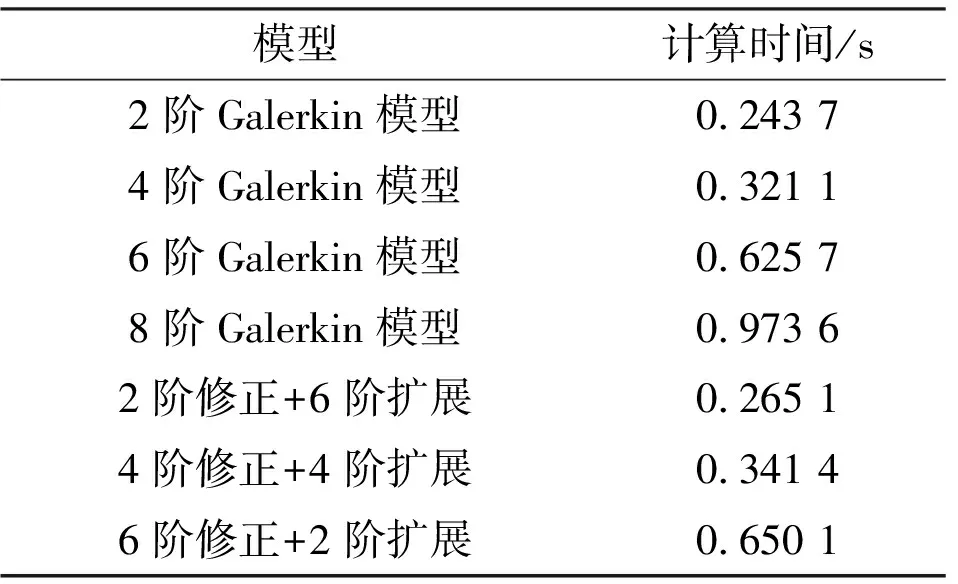
表4 不同模型计算时间对比

4 结 论

本文利用两个长短期记忆神经网络建立了从POD-Galerkin降阶模型到实际POD模态时间系数之间的修正映射以及低阶模态时间系数与高阶模态时间系数之间的扩展映射,通过修正映射和扩展映射分别消除标准POD-Galerkin降阶模型误差累积和扩展降阶模型阶数,构建了改进的POD-Galerkin降阶模型。将改进模型应用于二维圆柱绕流的流场预测,对模型的精度和计算时间进行了对比分析。本文主要研究结论如下。

(1)改进的POD-Galerkin降阶模型是数据驱动和物理驱动的混合模型,其在保留侵入式降阶模型的物理背景及可解释性的情况下,利用长短期记忆神经网进行修正和扩展,通过Galerkin投影框架、LSTM修正和LSTM扩展共3个层次准确描述流场变化。

(2)添加长短期记忆神经网络修正后的降阶模型与标准POD-Galerkin降阶模型相比更为准确。在相同阶数的降阶模型中,修正后的降阶模型更贴近实际POD结果,修正后模型各阶模态的均方根误差均较标准POD-Galerkin降阶模型要小1～2个数量级。

(3)添加长短期记忆神经网络扩展项后的改进降阶模型在与高阶POD-Galerkin降阶模型预测精度相近的情况下,改进降阶模型的计算时间要显著小于原始相同阶数的标准POD-Galerkin降阶模型。在精度基本不变的情况下,4阶和6阶改进降阶模型的计算速度相较于8阶标准POD-Galerkin降阶模型分别提高了约56%和25%。