Uncertainties of ENSO-related Regional Hadley Circulation Anomalies within Eight Reanalysis Datasets

Yadi LI ,Xichen LI ,Juan FENG,3 ,Yi ZHOU ,Wenzhu WANG ,and Yurong HOU

1International Center for Climate and Environment Sciences (ICCES), Institute of Atmospheric Physics,Chinese Academy of Sciences, Beijing 100029, China

2University of Chinese Academy of Sciences, Beijing 101408, China

3College of Global Change and Earth System Science (GCESS), Beijing Normal University, Beijing 100875, China

ABSTRACT El Niño–Southern Oscillation (ENSO),the leading mode of global interannual variability,usually intensifies the Hadley Circulation (HC),and meanwhile constrains its meridional extension,leading to an equatorward movement of the jet system.Previous studies have investigated the response of HC to ENSO events using different reanalysis datasets and evaluated their capability in capturing the main features of ENSO-associated HC anomalies.However,these studies mainly focused on the global HC,represented by a zonal-mean mass stream function (MSF).Comparatively fewer studies have evaluated HC responses from a regional perspective,partly due to the prerequisite of the Stokes MSF,which prevents us from integrating a regional HC.In this study,we adopt a recently developed technique to construct the three-dimensional structure of HC and evaluate the capability of eight state-of-the-art reanalyses in reproducing the regional HC response to ENSO events.Results show that all eight reanalyses reproduce the spatial structure of HC responses well,with an intensified HC around the central-eastern Pacific but weakened circulations around the Indo-Pacific warm pool and tropical Atlantic.The spatial correlation coefficient of the three-dimensional HC anomalies among the different datasets is always larger than 0.93.However,these datasets may not capture the amplitudes of the HC responses well.This uncertainty is especially large for ENSO-associated equatorially asymmetric HC anomalies,with the maximum amplitude in Climate Forecast System Reanalysis (CFSR) being about 2.7 times the minimum value in the Twentieth Century Reanalysis (20CR).One should be careful when using reanalysis data to evaluate the intensity of ENSO-associated HC anomalies.

Key words: regional Hadley circulation,ENSO,atmosphere-ocean interaction,reanalysis data

1.Introduction

Hadley circulation (HC) is one of the most important large-scale atmospheric circulations in the global climate system.It is characterized by warm air rising near the equator and cold air sinking in the subtropics,accompanied by a poleward wind in the upper troposphere and an equatorward wind in the lower troposphere (Hadley,1735;Bjerknes,1966;Lorenz,1967;Webster,2004).HC shows strong seasonality (Oort and Rasmusson,1970;Newell,1972;Cook,2003;Dima and Wallace,2003),with the strongest circulation appearing in the winter hemisphere.The rising and sinking branches of HC are tightly associated with tropical convective precipitation and subtropical drought,respectively (Diaz and Bradley,2004;Seidel et al.,2008).HC plays an important role in the global energy and mass balance (Held and Hou,1980;Held,2001;Trenberth and Stepaniak,2003),and has broad implications for the subtropical jet (Seager et al.,2003;Lu et al.,2008),subtropical droughts (Webster,2004;Hu and Fu,2007),global monsoon systems (Newell,1972;Dima and Wallace,2003),and the evolution of tropical ocean variability (Bjerknes,1966;Oort and Yienger,1996;Alexander et al.,2002;Döös and Nilsson,2011).

El Niño–Southern Oscillation (ENSO) dominates the interannual variability of the global climate system,which may drive a large-scale adjustment of the HC (Oort and Yienger,1996;Robinson,2002;Quan et al.,2004;Lu et al.,2008;Feng and Li,2013;Sun and Zhou,2014).The equatorial Pacific sea surface temperature (SST) warming associated with El Niño events (Oort and Yienger,1996;Quan et al.,2004) intensifies the HC,but constrains its extension in the meantime,leading to an equatorward movement of the jet system (Seager et al.,2003;Lu et al.,2008;Grise and Thompson,2012;Adames and Wallace,2017).In addition,the seasonal phase-locking of the ENSO system (Tziperman et al.,1994;Galanti and Tziperman,2000;Neelin et al.,2000;Wengel et al.,2018) leads to distinct HC adjustments between the El Niño developing year and decaying year (Wang,2002;Sun and Zhou,2014;Guo and Tan,2018).The adjustment of HC and its associated atmosphere–ocean interactions may also affect the ENSO system.(Lindzen,1994;Held,2001;Li et al.,2023).It is therefore important to clarify the effects of ENSO on HC on both regional and seasonal scales.

Given that there are no direct observations of HC,reanalysis datasets thus serve as an alternative proxy,which plays a crucial role in the investigation of HC and its interaction with ENSO events (Wang,2002;Trenberth and Stepaniak,2003;Quan et al.,2004;Nguyen et al.,2013;Li et al.,2023).Reanalysis data are obtained by quality control and assimilation of data from various sources,including atmospheric models and observations (Rakhmatova et al.,2021).As a result,it is a fundamental task to evaluate the quality of these state-of-the-art reanalysis datasets in representing the influence of ENSO events on HC.Previous studies indicate that a large diversity exists among different reanalysis datasets in reproducing the intensity of the ENSO-associated HC anomaly (Stachnik and Schumacher,2011;Nguyen et al.,2013;Sun and Zhou,2014).However,these works mainly focused on the HC response from a global perspective,which is represented by changes of the zonal-mean mass stream function (MSF) all around the globe (Stachnik and Schumacher,2011;Nguyen et al.,2013;Sun and Zhou,2014),partly due to the nondivergent prerequisite of the Stokes MSF (Palmén and Vuorela,1963;Vuorela and Tuominen,1964;Oort and Rasmusson,1970).

Nevertheless,the ENSO-associated anomalous circulation usually exhibits a strong regionality (Rasmusson and Carpenter,1982;Wallace et al.,1998;Wang,2002;Timmermann et al.,2018;Li et al.,2023).In particular,the intensity and the extension of HC are characterized by a clear regional feature (Chen et al.,2014;Schwendike et al.,2015;Freitas et al.,2017;Kim et al.,2017),which may not be well represented by a zonal-mean MSF (Oort and Yienger,1996;Quan et al.,2004;Lu et al.,2008).To overcome this disadvantage,recent studies (Zhang and Wang,2013,2015;Feng et al.,2018;Nguyen et al.,2018;Schwendike et al.,2021;Galanti et al.,2022;Li et al.,2022,2023) have proposed a technique to calculate the regional MSF by decomposing the atmospheric velocity field to its irrotational and nondivergent components.This approach enables the reconstruction of a threedimensional structure of the HC to investigate its responses to ENSO events.In this study,we evaluate the capabilities of eight frequently used reanalysis datasets in capturing the three-dimensional structure of the HC corresponding to the ENSO SST variability.In section 2,we briefly introduce the datasets and methods used in this study,with section 3 presenting the evaluation results of the El Niño-induced HC anomalies in eight reanalysis datasets.Section 4 gives the conclusions with a discussion of the results.

2.Datasets and methods

2.1.Reanalysis datasets

We use eight reanalysis datasets: (1) the National Centers for Environmental Prediction Climate Forecast System Reanalysis (CFSR;Saha et al.,2010) with a horizontal resolution of 2.5° × 2.5° and 37 vertical levels;(2) the European Centre for Medium-Range Weather Forecasts Interim Reanalysis [ERA-Interim (ERAI);Dee et al.,2011] with a horizontal resolution of 2.5° × 2.5° and 37 vertical levels;(3) the fifth generation European Centre for Medium-Range Weather Forecasting Reanalysis (ERA5;Hersbach et al.,2020) with a horizontal resolution of 0.25° × 0.25° 37 vertical levels;(4) the Japanese Meteorological Agency’s 55-year Reanalysis(JRA55;Kobayashi et al.,2015) with a horizontal resolution of 1.25° × 1.25° and 37 vertical levels;(5) the Modern-Era Retrospective Analysis for Research and Applications Version 2 (MERRA2;Gelaro et al.,2017) with a horizontal resolution of (2/3)°×(1/2)° and 42 vertical levels;(6) the Modern-Era Retrospective Analysis for Research and Applications (MERRA;Rienecker et al.,2011) with a horizontal resolution of (2/3)°×(1/2)° and 42 vertical levels;(7) the NCEPDOE Reanalysis II (NCEP2;Kanamitsu et al.,2002) with a 2.5° × 2.5° horizontal resolution and 17 vertical levels;and(8) the Twentieth Century Reanalysis (20CR;Compo et al.,2011) with a 2° × 2° horizontal resolution and 24 vertical levels.The monthly mean horizontal velocity of these reanalysis datasets is used to construct the three-dimensional structures of the ENSO-related HC,whose uncertainties are evaluated in this study.The precipitation of these datasets is also used to better understand the uncertainty of the regional HC.Here,the available time period within 1979–2019 is used for the analysis.

In order to compare the atmospheric circulations among different datasets,we use bilinear interpolation (on each level) and linear interpolation (for each vertical profile) to interpolate these variables to a uniform coordinate,with a horizontal resolution of 2° × 2° and 20 vertical levels.

We use the global Extended Reconstructed SST,version 5 (ERSST.v5;Huang et al.,2017) to calculate the SST variabilities associated with ENSO events–namely,the Niño-3.4 index,defined as the average SSTA over the region(5°S–5°N,120°–170°W).

2.2.Global HC

HC is usually described by a two-dimensional MSF on the latitudinal–vertical coordinate.According to Stokes’ theorem,one can calculate the MSF by integrating the meridional wind along the vertical direction or integrating the vertical velocity along the meridional direction.These two values are equal to each other when the velocity field is nondivergent,and only under this premise can the Stokes stream function Ψ(y,p) be calculated (Palmén and Vuorela,1963;Oort and Rasmusson,1970;Oort and Yienger,1996).As a result,one can integrate the global HC based on the zonal-mean meridional velocity all around the globe (Palmén and Vuorela,1963;Oort and Rasmusson,1970;Oort and Yienger,1996),given that the periodic boundary condition makes this zonal-mean velocity nondivergent:

where Ψ(y,p) is the Stokes stream function,gis the gravitational acceleration,ν and ω are the meridional and vertical velocity,Ris the radius of the Earth,and ϕ andpare the latitude and pressure.The overbar and brackets represent the temporal average and global zonal average,respectively.

A positive MSF (usually over the Northern Hemisphere)represents a clockwise meridional overturning circulation that rises at the equator and sinks in the subtropics of the Northern Hemisphere,while a negative MSF represents an anticlockwise meridional circulation.

2.3.HC from a regional perspective

Recent studies have developed new techniques to calculate the MSF of a regional HC by decomposing the horizontal velocity field at each pressure level into its irrotational and nondivergent components (Zhang and Wang,2013,2015;Nguyen et al.,2018;Feng et al.,2018;Schwendike et al.,2021;Galanti et al.,2022;Li et al.,2022,2023).The local MSF Ψ(x,y,p) can be derived by vertically integrating the irrotational meridional wind νdfrom the top to the bottom of the atmosphere:

Based on this method,we first decompose the horizontal velocity at each pressure level (Fig.1a) to obtain the irrotational velocity,and then integrate its meridional components from the top of the atmosphere to the bottom at each longitude(Fig.1b shows three profiles of the regional MSF,whose longitudes are marked in Fig.1a),to obtain a three-dimensional MSF of the HC all around the globe.

Fig.1.Schematic of the regression pattern of the three-dimensional MSF against the NDJ Niño-3.4 index: (a) Lead regression pattern of the annual mean 1000 hPa horizontal wind (units: m s-1 K-1) against the NDJ Niño-3.4 index based on the ensemble mean of the eight reanalysis datasets.The horizontal wind is then decomposed into the irrotational and nondivergent components.(b) Vertical structure of the lead regression pattern of the local MSF (units: kg s-1 K-1),which is obtained by vertically integrating the irrotational meridional wind at some longitudes marked red in panel (a).The vertical coordinate of (b) is pressure with unit of hPa.(c) Horizontal distribution of the intensity of the lead regression pattern of the MSF at each grid point,with solid (dashed) contours representing the positive (negative) values of the annual mean climatological state of the local MSF (units: 108 kg s-1).The Roman numerals represents six Hadley cells (Cells I–VI).Stippling indicates values with a significance level <0.05.

We then calculate the climatological state of the HC (contours in Fig.1c),as well as the ENSO-related HC anomaly(shading in Fig.1c) by regressing this three-dimensional HC against the Niño-3.4 index,and project the intensity of this three-dimensional HC on the horizontal plane (shading in Fig.1c).The intensity at each grid point in Fig.1c is defined as the maximum absolute value in the vertical profile above this grid.The positive values (red shading and solid contours in Fig.1c) represent the clockwise circulation with northward velocity in the upper troposphere and southward velocity in the lower troposphere,whereas the negative values represent the anticlockwise circulation.

Given that the SST and wind fields associated with ENSO events exhibit a seasonal phase-locking,with the strongest ENSO signal usually occurring in the November and December of the ENSO developing year (year0) and the January of the ENSO decaying year (year1),we use lead–lag regression in this study to project the three-dimensional MSF (of the developing year,or of each season in the developing and decaying years) onto the seasonal-mean November(year0),December(year0),January(year1) (NDJ)Niño-3.4 SST index,in order to examine the three-dimensional structure of the HC anomalies associated with ENSO events.

2.4.Symmetric and asymmetric components of HC

In this study,the three-dimensional HC associated with ENSO events is divided into the equatorial-symmetric component and the equatorial-asymmetric component based on the direction of the overturning circulation in the Northern and Southern Hemispheres (Feng et al.,2016).For the symmetric component,the MSF in the two hemispheres is in opposite directions (clockwise and anticlockwise),both rising (sinking) at the equator and sinking (rising) at higher latitudes:

For the asymmetric component of HC,the MSF in the two hemispheres is in the same direction:

We also decompose precipitation into its symmetric and asymmetric components,with the former representing the same values of precipitation in both hemispheres,and the latter with opposite values between the two hemispheres:

2.5.Statistical methods

We use lead–lag regression to investigate the threedimensional features of the HC associated with El Niño events for each season.Student’st-test is used to examine the statistical significance level of the regression coefficients.We calculate the three-dimensional spatial correlation to quantify the similarity among the eight reanalysis datasets.

3.Results

3.1.ENSO-associated HC anomalies in a regional perspective

We first illustrate the three-dimensional structure of the ENSO-associated HC based on the ensemble mean of the eight reanalysis datasets.Figure 1c shows the horizontal distribution of the anomalous MSF associated with El Niño,based on the linear lead regression coefficients of the annual mean regional HC against the NDJ Niño-3.4 index,with a positive value (red) showing clockwise overturning circulation and a negative value (blue) indicating anticlockwise circulation.The global HC anomaly can be divided into six subcells naturally (Cells I–VI in Fig.1c;hereafter also referred to simply as the Hadley cells),according to the boundary of positive and negative values of the MSF (e.g.,the segmentation of Cell I and II) or the minimum (absolute) values of the MSF (e.g.,the segmentation of Cell I and IV).The local MSF within each Hadley cell is always positive or negative,thus avoiding cancellation of the cumulative MSF within a single cell.We then calculate the vertical structure of the Hadley cells (Figs.2a–c) by zonally integrating each cell,and the vertical structure of the global HC (Fig.2d) by summing these cells.

Fig.2.Vertical structure of the ENSO-related regional MSF of each pair of Hadley cells over (a) the Indo-Pacific warm pool,(b) the central-eastern Pacific Ocean,(c) the Atlantic Ocean,and (d) the globe.The sum of three pairs of Hadley cells leads to the cancellation of positive and negative values,resulting in a global narrow meridional circulation.The vertical coordinate is pressure with unit of hPa.

As shown in Fig.1c and Fig.2,the climatological state of the HC (contours in Fig.1c) always rises over the equator but sinks over the sub-tropics,while the response of HC to an El Niño event is constructed by three pairs of Hadley cells.Each pair is located on the two sides of the equator,and with opposite directions of overturning circulation (shading in Fig.1c and Fig.2).In particular,Cells I and II (shading in Fig.1c and Fig.2a) are located over the Northern and Southern Hemispheres around the Indo-Pacific warm pool region,respectively,extending from about 60°E to 150°E.These HC anomalies associated with El Niño events are opposite to the climatological state of the HC (contours in Fig.1c) and represent a weakening of HC over the Indo-western Pacific in response to the ENSO SST forcing.Cells III and IV (shading in Fig.1c and Fig.2b) are over the tropical central-eastern Pacific,driven by the El Niño-induced SST warming and its associated deep atmospheric convection over the central-eastern Pacific.The HC over the central-eastern Pacific has been dramatically intensified (Rasmusson and Carpenter,1982;Wallace et al.,1998).The opposite influence of these two pairs of Hadley cells over the Indo-western Pacific warm pool and the central-eastern Pacific is closely related to the ascending and descending branches of the Walker circulation,which weakens during El Niño.Cells V and VI (shading in Fig.1c and Fig.2c) are located over the tropical Atlantic.This anomaly represents a slight weakening of the HC over the tropical Atlantic.It is interesting that the regional HC shows a wide extent,with the poleward edge north of 25°N or south of 25°S,while the global HC is confined to within 20°N/S,possibly due to the cancellation of the clockwise and anticlockwise circulation over different regions when integrating all over the globe (Fig.2d).The vertical structure of Cells III,IV,V,and VI (Fig.2b and c),as well as that of the global HC (Fig.2d),exhibit clear equatorially asymmetric features,which will be further discussed later in the paper.

3.2.Spread of the HC response among different reanalysis datasets

The above features of the ENSO-associated HC anomaly are based on the ensemble mean of eight reanalysis datasets.To further evaluate the coherency and diversity among these datasets in representing the three-dimensional structure of the anomalous HC associated with ENSO events,we illustrate the horizontal and vertical structures of the ENSO-associated HC anomaly in each of these eight reanalyses in Fig.3.The color shading represents the lead regression coefficients of the annual mean regional HC against the NDJ Niño-3.4 index for each reanalysis,while the contours show the precipitation anomalies associated with ENSO events (by regression) in these datasets.

Fig.3.Horizontal distribution and vertical structure of the annual mean ENSO-related MSF (shading,units: kg s-1 K-1) in the eight reanalysis datasets.Green and brown contours represent the lead regression pattern of the annual mean precipitation (units:mm d-1 K-1,with green/brown contours representing positive/negative values) against the NDJ Niño-3.4 index.The vertical coordinate of right panles is pressure with unit of hPa.

The horizontal distribution of the regional HC anomaly associated with ENSO events in each of the reanalysis datasets shows a similar pattern (Fig.3) to the three pairs of Hadley cells,accompanied by intensified precipitation(green contours in Fig.3) over the equatorial central-eastern Pacific and weakened precipitation (red contours) over the Maritime Continent and some areas of the equatorial Atlantic.The intensified precipitation is tightly associated with enhanced deep atmospheric convection,agreeing well with the strengthened regional HC around the equatorial central-eastern Pacific (Fig.3a).In contrast,the weakened precipitation may lead to a weakening of the regional HC around the Indo-western Pacific warm pool and over the tropical Atlantic (Figs.3a–h).These features are seen in all the reanalysis datasets,with strong coherency in the horizontal patterns of the regional HC among them (left panels of Figs.3a–h).However,the intensity of the HC is distinct across the different datasets,which is more evident in the vertical profiles of HC in the right panels of Figs.3a–h than the horizontal patterns of HC in the left panels of Figs.3a–h.Meanwhile,the differences in HC intensity are accompanied by differences in associated precipitation anomalies–for example,the precipitation anomaly is weakest in 20CR,whose HC response is also the weakest (Fig.3h).

To better quantify the regional HC over different ocean basins,we integrate the regional MSFs over different sectors including the Indo-western Pacific warm pool,the centraleastern Pacific,and the Atlantic Ocean (shading in Fig.4),and plot them together with the regional (zonal) integrated curves of precipitation anomalies (curves in Fig.4,with solid curves illustrating the regional precipitation in the reanalyses and dashed curves those of the observations).There is a minimum (<0) value of precipitation anomalies over the equator of the Indo-western Pacific warm pool and the tropical Atlantic,representing the descending branches of the anomalous Hadley cells (Cells I and II,Cells V and VI)over these areas in relation to an El Niño event.In contrast,there is a maximum (>0) value of precipitation anomalies to the north of the equator over the central-eastern Pacific,corresponding to the ascending branch of the Hadley cells(Cells III and IV).In the central-eastern Pacific,the regional precipitation anomalies of NCEP2 are relatively stronger,with a slight shift in the location of the maximum value in comparison to that in the observations (Fig.4g).In addition,there is the weakest pair of Hadley cells (Cells III and IV)in 20CR accompanied by the weakest regional precipitation anomalies (Fig.4h).These features agree well with the deviations in the regional HC.

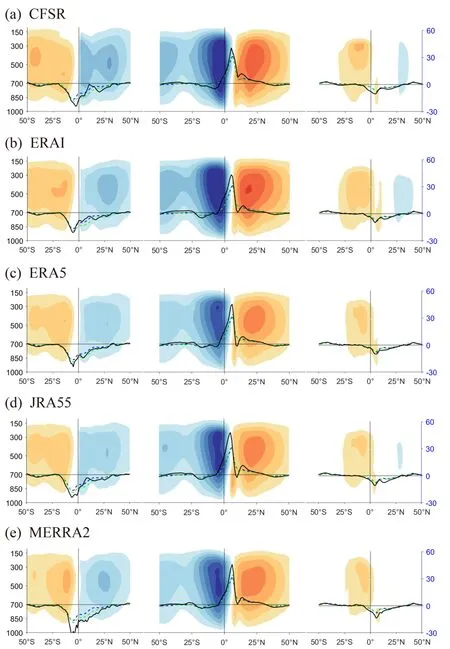
Fig.4.Vertical structure of the annual mean ENSO-related regionally integrated MSF (shading;units: kg s-1 K-1)of each pair of Hadley cells in the eight reanalysis datasets.The curves in the vertical structure represent the regionally integrated precipitation anomalies (coordinate on the right,units: mm d-1 K-1) in the eight reanalyses and observations,with black solid curves representing each reanalysis’ precipitation,green dashed curves representing CMAP data,and dark blue dashed curves representing GPCP data.The vertical coordinate (on the left) is pressure with unit of hPa.

To further quantify the coherency and diversity between different reanalysis datasets,we calculate the spatial correlation of the three-dimensional HC associated with ENSO events in all reanalysis datasets (Fig.5a),and compare them with the ensemble mean of these datasets (first row/column in Fig.5a).The three-dimensional spatial correlations between each pair of reanalysis datasets (including their ensemble mean) are all above 0.9 (Fig.5a),which confirms the coherency of the ENSO-associated three-dimensional HC anomaly between these reanalysis datasets.In particular,the correlation coefficients between ERA5,ERAI,JRA-55,and the ensemble-mean are larger than 0.97.This strong consistency implies the robustness of these state-of-the-art reanalysis datasets in representing the regional HC response to ENSO events.NCEP2 and 20CR (Fig.5a) share the lowest correlation with the other reanalyses,but are still larger than 0.9.

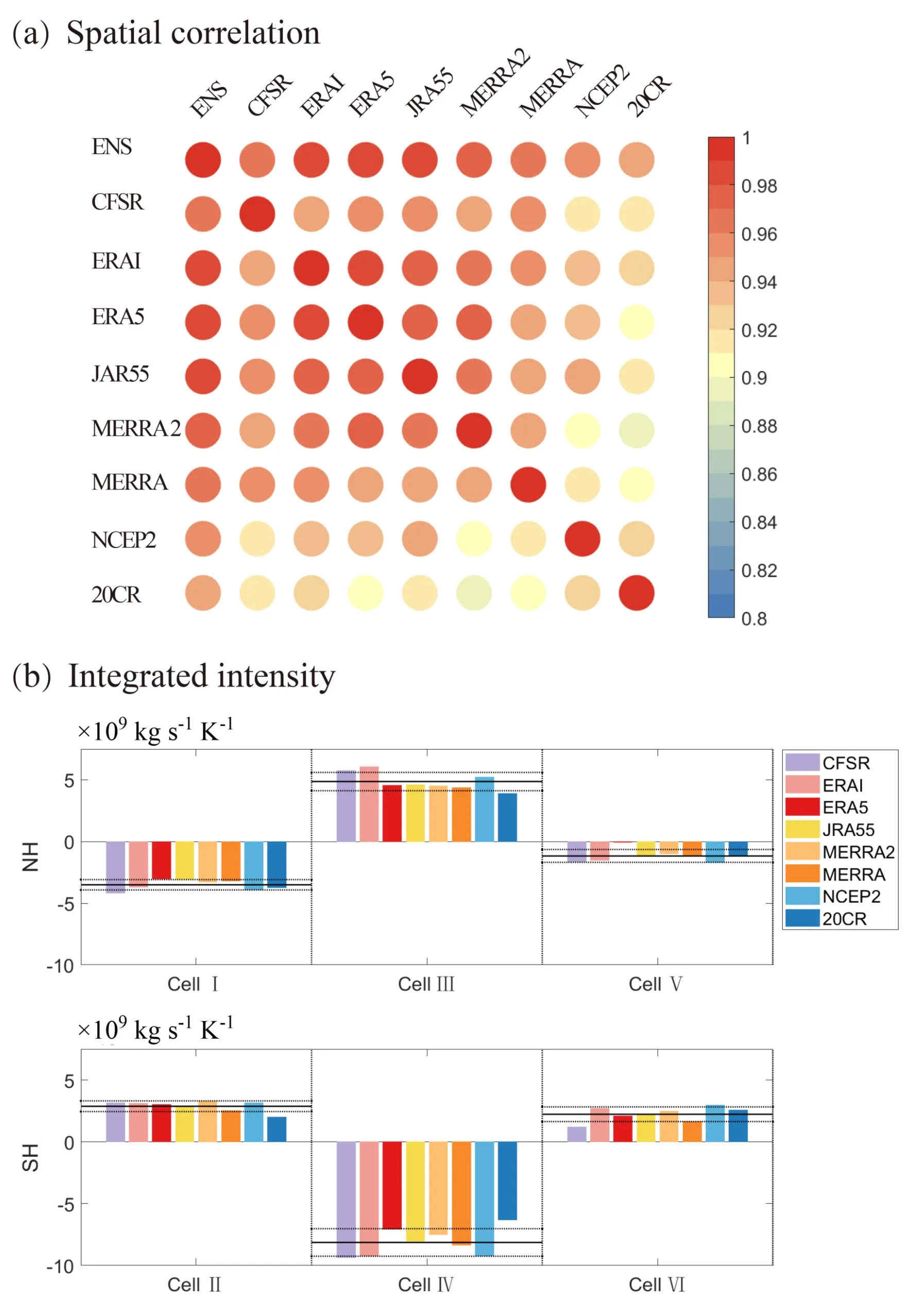
Fig.5.Quantification of the spread of the lead regression pattern of the annual mean three-dimensional MSF and the integrated intensity of each Hadley cell anomaly among each reanalysis dataset.(a) The three-dimensional spatial correlation between each pair of the eight reanalysis datasets,including the ensemble mean of all reanalyses.(b) The integrated amplitude of each regional Hadley cell anomaly in each reanalysis dataset.The solid lines represent the amplitude of the multi-reanalysis ensemble.The dotted lines indicate ±1 standard deviation of the amplitude in the eight reanalyses.

Nevertheless,the amplitudes of the ENSO-associated HC anomaly vary among the different datasets (Fig.3).To clarify these differences,we further quantify the amplitudes of the six sub-cells in each reanalysis dataset in Fig.5b.Among these sub-cells,those around the central-eastern Pacific (Cell III and Cell IV) show the most pronounced deviations among the different datasets,with the ENSO-associated circulation adjustment in Cell III (Fig.5b) reaching between 3.92 × 109kg s-1K-1and 6.09 × 109kg s-1K-1among all eight datasets,and that of Cell IV varying between -6.32 × 109kg s-1K-1and -9.35 × 109kg s-1K-1.In particular,CFSR,ERAI and NCEP2 have a stronger circulation response to ENSO SST forcing (Figs.3a,b and g) for most of the six sub-cells (Fig.5b),whereas 20CR shows a weaker circulation response,accompanied by a weaker precipitation anomaly in comparison to any of the other datasets(Fig.3h).Further analysis indicates that 20CR may considerably underestimate Cell III and Cell IV (Fig.5b),as well as the sub-cell over the Southern Hemisphere Indo-western Pacific (Cell II;Fig.5b).

Considering that the above analyses are all based on reanalysis datasets,it is hard to evaluate the deviation of each reanalysis in comparison to observations (which do not exist).However,given the strong relationship between tropical convective precipitation and the HC,we can use precipitation observations (CMAP and GPCP) as references to evaluate each reanalysis dataset (Fig.6).The deviations between ERAI (Fig.6b),ERA5 (Fig.6c),MERRA (Fig.6e),MERRA2 (Fig.6f),and the observational precipitation are relatively small.In contrast,the deviations of NCEP2 (Fig.6g) and 20CR (Fig.6h) are very large.This result agrees well with that of the regional HC.

Fig.6.Deviation of the annual mean ENSO-related precipitation (shading;units: mm d-1 K-1) between each reanalysis dataset and the average value of CMAP and GPCP.

In addition,the spatial structure of the ENSO-associated HC anomaly (Fig.3) shows some asymmetric features relative to the equator.This equatorially asymmetric feature is especially pronounced in the vertical profiles of the global HC anomaly (Figs.3a–h;right panels),characterized by a strong anticlockwise circulation anomaly (blue shading)over the equator (Figs.3a–h;right panels),and with a large diversity among different datasets.This feature motivates us to further investigate the ENSO-associated symmetric and asymmetric HC anomalies and their diversity among different reanalysis datasets.

3.3.The equatorially symmetric and asymmetric features of the HC response

While the equatorially symmetric HC plays an important role in the mass and energy transport between the tropics and midlatitudes,the equatorially asymmetric components contribute more to the mass and energy transport between the Northern and Southern Hemispheres (Oort and Rasmusson,1970;Lindzen and Hou,1988;Held,2001).We thus further decompose the ENSO-associated HC anomaly into its symmetric and asymmetric components.Figures 7a and b show the horizontal distribution (color shading in Fig.7a)and vertical structure (Fig.7b) of the equatorially symmetric component of the El Niño-induced regional HC anomaly based on the ensemble mean of all eight reanalyses,accompanied by the equatorially symmetric components of the ENSO-associated precipitation (contours in Fig.7a),while Figs.7c and d show those of the equatorially asymmetric component.

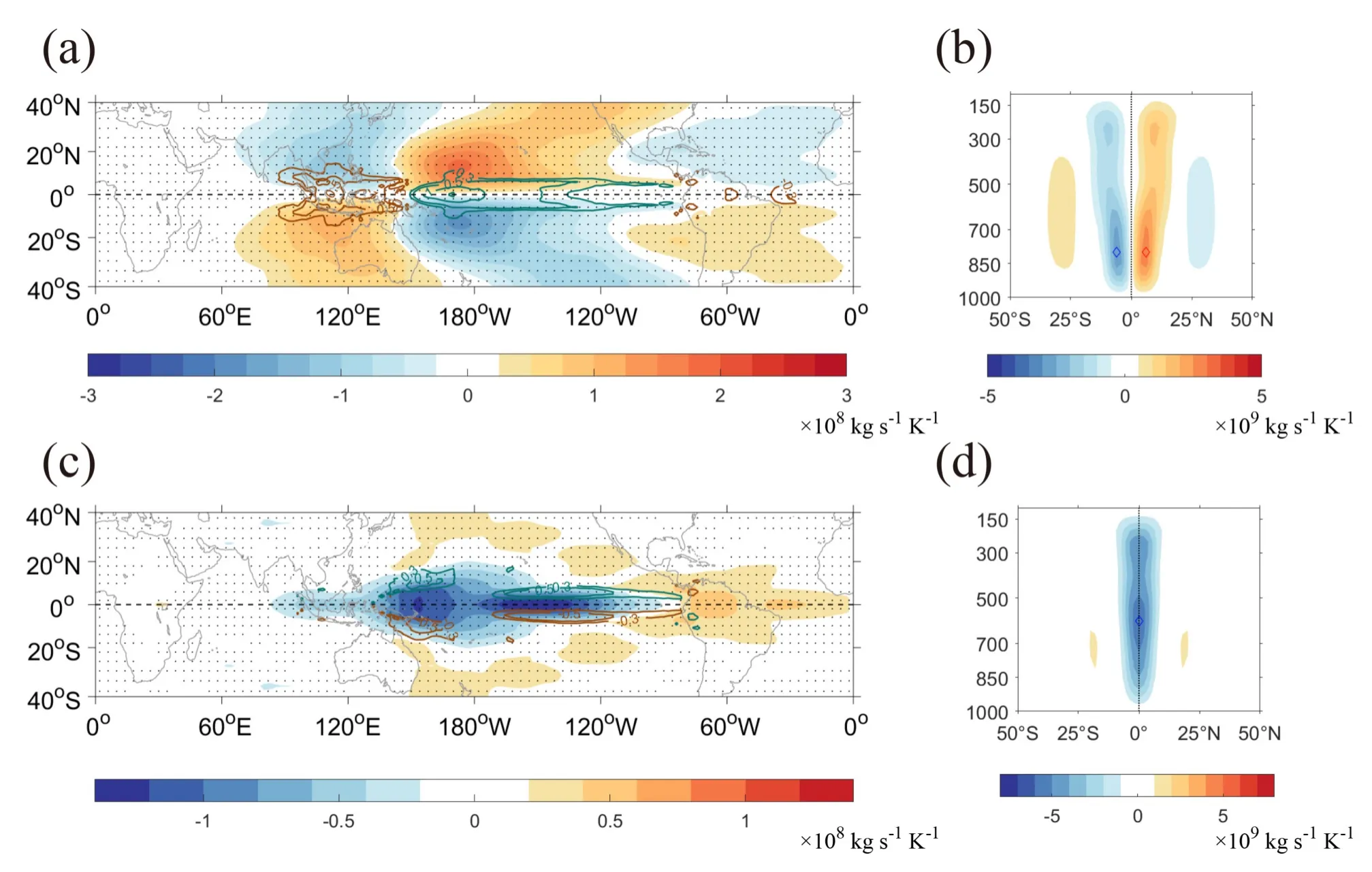
Fig.7.Horizontal distribution and vertical structure of the equatorially symmetric and asymmetric components of the annual mean ENSO-related MSF (shading;units: kg s-1 K-1) and precipitation (contours;units: mm d-1 K-1) based on the ensemble mean of eight reanalysis datasets.(a,b) As in Fig.3a but for the equatorially symmetric component based on the ensemble mean of the eight reanalysis datasets.(c,d) As in (a,b) but for the equatorially asymmetric component.The vertical coordinates of (b)and (d) are pressure with unit of hPa.

The symmetric component exhibits strong regionality(Fig.7a),which can also be divided into three pairs of subcells (Fig.7a).On the other hand,the asymmetric component shows a dipole pattern over the tropics (Fig.7c),with a strong anticlockwise overturning circulation over the equatorial Pacific,extending from 90°E to 90°W,but a relatively weaker cross-equatorial clockwise circulation over the tropical Atlantic and South America.The former overcomes the latter,forming an overall anticlockwise asymmetric circulation around the equator in the ENSO-associated global HC anomaly (Fig.7d).

We further examine the consistency and diversity of the symmetric and antisymmetric components among the eight reanalysis datasets by calculating the three-dimensional spatial correlation (Figs.8a and c) among different datasets,whilst at the same time quantifying the amplitudes of the ENSO-associated symmetric/asymmetric circulation anomalies (Figs.8b and d) of each reanalysis.

The spatial correlations of the symmetric field between most pairs of the reanalysis datasets are higher than 0.96(Fig.8a),except those between NCEP2,20CR and the other reanalyses (whose correlations are～0.91).The spatial correlations of the symmetric component are higher than that of the original field.In contrast,the amplitudes of the symmetric components (Fig.8b) show strong diversity,ranging from 1.94 × 109kg s-1K-1(MERRA) to 3.73 ×109kg s-1K-1(NCEP2),with an ensemble mean value of 2.84 × 109kg s-1K-1.This large diversity re-emphasizes that the amplitudes of the HC response to ENSO events in these reanalysis datasets may suffer from large uncertainty.

In contrast to that of the symmetric circulation anomaly,the spatial correlations of the asymmetric components among different datasets (Fig.8c) are relatively lower.The spatial correlation coefficients of CFSR,MERRA,NCEP2,and 20CR with the other datasets are generally lower than 0.9,with a minimum value of about 0.8 between 20CR and MERRA2.Despite this large diversity among these datasets,we found that the spatial correlations between each pair of ERA5,ERAI,JRA-55,and MERRA2 (correlations marked by a red box in Fig.8) are relatively higher,reaching above 0.95.This similarity implies that the above reanalysis datasets (ERA5,ERAI,JRA-55,and MERRA2) may better capture the asymmetric feature of the HC anomaly in response to the ENSO event.

On the other hand,the spread of the amplitudes of the ENSO-associated asymmetric HC anomalies is even larger(Fig.8d),ranging from -3.34 × 109kg s-1K-1to -8.99 ×109kg s-1K-1,with an ensemble mean value of -6.14 ×109kg s-1K-1.The maximum value (in CFSR) is about 2.7 times the minimum value (in 20CR),indicating that current reanalysis datasets may not capture the amplitudes of the ENSO-associated asymmetric HC anomaly well.

Finally,we compare the horizontal distributions of these asymmetric HC responses for all eight reanalyses(Fig.9),to illustrate in detail the deviation among them.Most of the reanalyses (Figs.9a–e and g–h) capture the dipole-like asymmetric HC responses,with a cross-equatorial anticlockwise circulation anomaly over the equatorial Pacific (in response to El Niño events) and a weaker crossequatorial clockwise circulation over the Atlantic basin.However,the clockwise circulation is too weak to be reorganized in MERRA (Fig.9f).CFSR (Fig.9a) shows the strongest anticlockwise asymmetric circulation anomaly accompanied by the strongest precipitation anomaly over the equatorial Pacific,whereas 20CR (Fig.9h) shows the weakest circulation anomaly accompanied by the weakest precipitation anomaly,largely due to the deviation in the intensity and location of the tropical Pacific convection (contours in Figs.9a and h) in response to the ENSO SST variability,which is closely related to the convection parameterization scheme in the reanalysis datasets (Mitas and Clement,2005;Stachnik and Schumacher,2011;Nguyen et al.,2013;Zhang et al.,2013).In addition,the ENSO-associated clockwise circulation over the tropical Atlantic and South America is much stronger in 20CR (Fig.9h) than in any of the other reanalyses.These deviations limit the capability of these reanalysis datasets in capturing the spatial pattern and amplitude of the asymmetric components of the ENSO-associated HC response,which requires further investigation and improvement.

3.4.Seasonality of the ENSO-associated HC anomaly from a regional perspective

The evolution of an El Niño event is characterized by a strong seasonal phase-locking (Tziperman et al.,1998;Galanti and Tziperman,2000),with the equatorial centraleastern Pacific SST anomaly typically developing in the boreal summer (JJA) and autumn (SON) of the developing year (year0),peaking in the November,December and January (NDJ),and decaying rapidly in the spring of the following year (year1).Given that the ENSO-associated largescale circulation adjustment is mainly driven by the SST anomalies,we further investigate the regional HC response for each of these four seasons (JJA,SON and DJF of the developing year,and MAM of the decaying year).

Figure 10 shows the ENSO-associated regional HC anomaly (color shading in the first column;panels a–d),its symmetric components (second column;panels e–h),and its asymmetric components (third column;panels i–l) for all four seasons from the summer of the developing year[JJA(year0)] to the spring of the decaying year[MAM(year1)],with the contours in each panel representing the associated precipitation anomaly.

For all four seasons,the regional circulation in response to ENSO events can be divided into six sub-cells,similar to that of the annual-mean states (Fig.1c),but with the amplitudes increasing from the summer of the developing year (Fig.10a) to the ENSO peak season (Fig.10c),and decreasing in spring of the decaying year (Fig.10d).Similarly,the symmetric components of the anomalous HC for each season (Figs.10e–h) show an identical horizontal structure as their annual-mean states (Fig.7a),with a clear seasonal cycle peaking in the winter of the developing year(Fig.10g),which is synchronized with the peak of the ENSO event and the associated weakest Walker circulation(Tziperman et al.,1994;Jin et al.,1996).

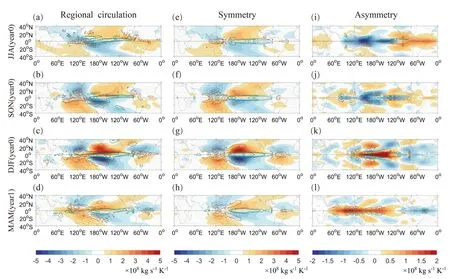
Fig.10.Horizontal distribution of the ENSO-related MSF (shading;units: kg s-1 K-1) and precipitation (contours;units: mm d-1 K-1)based on the ensemble mean of the eight reanalysis datasets,and their equatorially symmetric and asymmetric components for the four seasons of the ENSO developing and decaying year [JJA(year0),SON(year0),DJF(year0),and MAM(year1)].Panels(a–d) show the horizontal distribution of the regional HC responses to ENSO (by a lead–lag regression on the NDJ Niño-3.4 index).Panels (e–h) and (i–l) show the horizontal distribution of the equatorially symmetric and asymmetric components of the regional HC responses to ENSO,respectively.

Nevertheless,the ENSO-associated asymmetric HC anomalies for each season (Figs.10i–l) show distinct patterns(Fig.7c).For summer (Fig.10i) and autumn (Fig.10j) of the developing year,the asymmetric components of the HC anomaly are characterized by a cross-equatorial anticlockwise circulation over the equatorial Pacific,with a clockwise asymmetric circulation over the equatorial Atlantic,similar to that of the annual-mean states (Fig.7c).However,in DJF(year0) and MAM(year1),this asymmetric pattern reverses,with a cross-equatorial clockwise circulation over the equatorial Pacific but an anticlockwise circulation over the equatorial Atlantic,opposite to that of the annual-mean states (Fig.7c).This seasonal switch of the asymmetric HC response has been primarily attributed to the seasonal adjustment of the background SST over the tropical Pacific (Graham and Barnett,1987;Guo and Tan,2018) and the associated southward shift of the convergence zone in boreal winter.

We further evaluate the coherency and diversity of these seasonally varying HC responses among the different reanalysis datasets.Figure 11 shows the spatial correlation coefficients of the three-dimensional structure of the ENSOassociated HC anomalies (Figs.11a–d) among all reanalysis datasets,as well as its symmetric (Figs.11e–h) and asymmetric (Figs.11i–l) components for all four seasons.It can be seen that the cross-correlation between each pair of the regional HC responses (Figs.11a–d) is greater than 0.9 for all four seasons,whose features agree well with the crosscorrelation coefficients for the annual-mean states (Fig.5a),referring to a high coherency among these reanalyses that different datasets may capture an identical three-dimensional feature of the HC response during the developing and the decaying year of an El Niño event.The symmetric components(Figs.11e–h) show higher correlations for all four seasons.Remarkably,the correlation coefficients of the symmetric components between each pair of reanalysis datasets are very close to 1 for boreal winter [DJF(year0);Fig.11g].This high degree of correlation re-emphasizes that the spatial structure of the ENSO-associated HC anomaly,especially its symmetric component,can be very well represented in the present reanalysis datasets.

Fig.11.The three-dimensional spatial correlation of (a–d) the ENSO-related MSF and its (e–h) equatorially symmetric and (i–l)asymmetric components between each reanalysis dataset from the boreal summer of the developing year to the boreal spring of the decaying year.As in Fig.5a but for the four seasons [JJA(year0),SON(year0),DJF(year0),and MAM(year1)].

However,the cross-correlation coefficients of the asymmetric component are relatively lower for all four seasons.In SON(year0) and DJF(year0),the spatial correlations reduce to less than 0.8 for some pairs of reanalyses (especially MERRA and 20CR),which is even lower than that of the annual-mean states (Fig.8c).This diversity indicates that the reanalyses datasets may not represent the seasonal asymmetric response of the HC to the ENSO-related SST variability very well.

The amplitudes of the symmetric (Figs.12a–d) and asymmetric (Figs.12e–h) global HC responses in these reanalysis datasets for all four seasons are also calculated.The amplitudes of the symmetric components show a clear seasonal cycle (Figs.12a–d),increasing from JJA (Fig.12a) to DJF(Fig.12c) of the developing year,but decreasing in the MAM of the decaying year (Fig.12d).In contrast,the seasonal variation of the amplitudes of the asymmetric HC anomalies is relatively smaller (Figs.12e–h).Similar to that of the annual-mean states (Fig.8b,d),a large spread among different reanalyses exists for all four seasons in capturing the amplitudes of both the symmetric and asymmetric HC anomalies (Fig.12).This diversity is even more pronounced for the asymmetric components (Figs.12e–h),especially for that of the JJA(year0) (Fig.12e) and SON(year0) (Fig.12f).Remarkably,the amplitudes of the ENSO-associated asymmetric global HC anomalies for JJA(year0) (Fig.12e) and MAM(year1) (Fig.12h) are much larger than that of the symmetric HC anomalies (Figs.12a and d);while for the ENSO peak season,the amplitudes of the asymmetric components(Fig.12g) are comparable to those of the symmetric components (Fig.12c).The large spread of the ENSO-associated asymmetric HC anomalies in these reanalysis datasets revealed in this study thus raises a crucial issue–that the uncertainty in the reanalysis datasets may prevent us from achieving an accurate estimation of the ENSO-associated large-scale circulation adjustment,as well as the mass and energy budgets between the two hemispheres,which requires urgent investigation.

Fig.12.Quantification of the integrated amplitude of the equatorially symmetric and asymmetric components of the ENSO-related MSF from the boreal summer of the developing year to the boreal spring of the decaying year.As in Figs.8b and 8d but for the four seasons[JJA(year0),SON(year0),DJF(year0),and MAM(year1)].

To further clarify the spatial pattern of the diversity among different datasets,we illustrate the horizontal and vertical structures of the ENSO-associated asymmetric HC anomalies for two seasons [SON(year0) in Fig.13,and DJF(year0)in Fig.14],given that the direction of the asymmetric HC anomalies reverses before and after the ENSO peak season(Figs.10i–l).The former (Fig.13) is before the ENSO peak season and characterized by an anticlockwise cross-equatorial circulation anomaly over the tropical Pacific,whereas the latter (Fig.14) is after the peak season and characterized by a clockwise cross-equatorial circulation anomaly,both suffering from relatively low cross-correlation coefficients(Figs.11j and k) and a large spread in amplitude among the different reanalyses (Figs.12f and g).

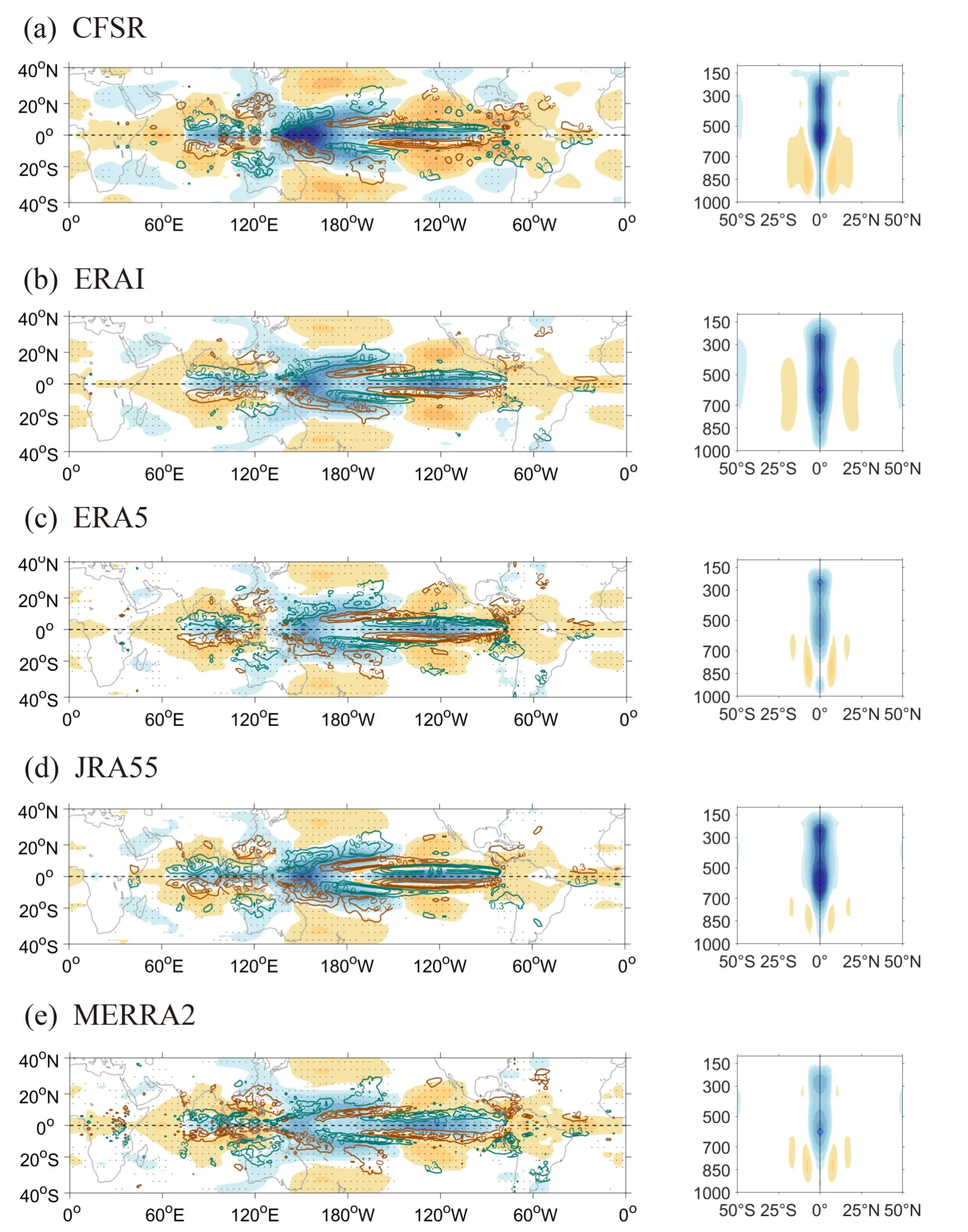
Fig.13.Horizontal distribution and vertical structure of the equatorially asymmetric components of the ENSO-related MSF(shading;units: kg s-1 K-1) and precipitation (contours;units: mm d-1 K-1) in the boreal autumn of the developing year for the eight reanalysis datasets.As in Fig.9 but for SON(year0).The vertical coordinate of right panels is pressure with unit of hPa.

Fig.14.Horizontal distribution and vertical structure of the equatorially asymmetric components of the ENSO-related MSF(shading;units: kg s-1 K-1) and precipitation (contours;units: mm d-1 K-1) in the boreal winter of the developing year for the eight reanalysis datasets.As in Fig.9 but for DJF(year0).The vertical coordinate of right panels is pressure with unit of hPa.

While the asymmetric HC anomalies in most of the reanalyses in SON(year0) (Fig.13) are characterized by an anticlockwise overturning circulation over the tropical Pacific but a weaker clockwise circulation over the tropical Atlantic,the asymmetric HC anomalies in MERRA(Fig.13f) show a cross-equatorial anticlockwise circulation all around the globe,which is due to a relatively weaker positive precipitation anomaly over the South Atlantic.On the other hand,the clockwise circulation anomaly over the tropical Atlantic in 20CR (Fig.13h) is comparatively too strong,extending to the eastern Pacific,accompanied by a weaker anticlockwise circulation over the tropical Pacific.The difference in 20CR is due to a relatively stronger positive precipitation anomaly over the Pacific Coast of South America and the South Atlantic and a relatively weaker negative precipitation anomaly over the South Pacific.

In boreal winter [DJF(year0);Fig.14],the clockwise circulation anomaly over the tropical Pacific (Fig.14f) in MERRA is relatively stronger than that in the other reanalyses,extending to the entire Indian Ocean and Africa as well.This anomaly leads to a much stronger asymmetric global HC response (right panel of Fig.14f) in comparison to that of any other reanalyses.

4.Discussion and conclusions

The HC adjustment induced by ENSO events has profound implications for the climate variability in the tropics and subtropics.However,direct observations of large-scale atmospheric meridional overturning circulation are not yet available.As an alternative proxy,reanalysis datasets play important roles in the investigation of HC anomalies,meaning it is important to assess their uncertainty in representing the HC response to ENSO events.Previous studies typically addressed this issue from a global perspective of HC (Stachnik and Schumacher,2011;Nguyen et al.,2013;Sun and Zhou,2014),largely due to the prerequisite of the Stokes MSF,which prevents us from integrating a regional HC.However,recent studies have developed new techniques to construct the three-dimensional structure of HC with the irrotational components of the meridional velocity (Zhang and Wang,2013,2015;Feng et al.,2018;Nguyen et al.,2018;Schwendike et al.,2021;Galanti et al.,2022;Li et al.,2023),motivating us to perform a systematic evaluation of the three-dimensional regional HC response to ENSO SST forcing based on eight state-of-the-art reanalysis datasets.

The horizontal distribution of the ENSO-associated HC anomaly can be divided into three pairs of sub-cells(Fig.1c),located around the Indo-Pacific warm pool region,the central-eastern Pacific,and the tropical Atlantic,respectively.The pair around the central-eastern Pacific Ocean intensifies the climatological states of the HC,while the other two weaken it over the Indo-western Pacific and the Atlantic basin.We further examine the diversity of the ENSO-associated circulation patterns among the different reanalyses.Results show that all reanalyses capture an identical spatial structure of the anomalous HC (Fig.3),with the spatial correlation coefficients of the three-dimensional HC anomaly between each pair of reanalyses being larger than 0.93,indicating that all reanalyses capture the spatial structure of the ENSO-associated HC anomaly well.However,large spread is seen in the amplitudes of the ENSO-associated regional HC anomalies among the different reanalysis datasets,implying that large uncertainty may exist among them in capturing the intensity of the ENSO-associated HC response.

We further evaluate the skills of these reanalysis datasets in representing the equatorially symmetric and asymmetric components of the ENSO-associated HC anomalies.Results show that all reanalyses represent the main feature of the symmetric components well by capturing an identical pattern among the different reanalyses,with spatial correlation coefficients larger than 0.96.However,while ERA5,ERAI,JRA-55 and MERRA2 capture a similar pattern of the asymmetric HC responses,the other reanalyses show different spatial structures,with spatial correlation coefficients lower than 0.8.Notably,three of the four reanalyses with higher spatial correlations (namely,ERAI,ERA5 and JRA-55,marked in Fig.8c),which are considered to have better quality,use a 4D-Var assimilation scheme,while the remaining one (MERRA2) uses another advanced assimilation scheme (3D-FGAT),and the others (CFSR,MERRA,NCEP2,and 20CR) use traditional 3D-Var assimilation schemes (Talagrand,2010;Fujiwara et al.,2017).On the other hand,the amplitudes of both the symmetric and asymmetric components show strong discrepancies among the different reanalyses,with the maximum value of the amplitude of the asymmetric HC anomaly (in CFSR) being about 2.7 times its minimum value (in 20CR).In short,20CR may not represent the amplitude and spatial structure of the ENSOrelated HC anomaly very well.A possible reason for this is that 20CR only assimilates near-surface observational data.Our results suggest that an advanced assimilation scheme and assimilating more observations in the troposphere (and stratosphere) may help to improve the capability of the reanalysis datasets in capturing the three-dimensional features of HC.

Given that El Niño events are characterized by a strong seasonal phase-locking (Tziperman et al.,1998;Galanti and Tziperman,2000;Neelin et al.,2000;Wengel et al.,2018),we also evaluate the capability of the reanalysis datasets in capturing the seasonal features of both symmetric and asymmetric HC anomalies.Again,all reanalyses capture the seasonal features of the ENSO-associated symmetric HC well,which is divided into three pairs of sub-cells,with an increased intensification before the ENSO peak season(NDJ) and a decreased amplitude afterwards.It is important to note that the amplitudes of the ENSO-associated asymmetric HC anomalies for JJA(year0) (Fig.12e) and MAM(year1) (Fig.12h) are larger than those of the symmetric components (Figs.12a and d),while the amplitudes of the asymmetric components for DJF (the ENSO peak season)are comparable to those of the symmetric components.This large amplitude of the asymmetric HC anomaly re-emphasizes the urgent need for better representation of the ENSOassociated asymmetric HC in these reanalysis datasets.These differences may be caused by the convection parameterization scheme used in the reanalysis data,which has broad implications for the ascending branch of HC (Mitas and Clement,2005;Stachnik and Schumacher,2011;Nguyen et al.,2013;Zhang et al.,2013).

HC plays a crucial role in the mass,momentum,and energy balances of the Earth system (Lindzen and Hou,1988;Lindzen,1994;Held,2001;Trenberth and Stepaniak,2003).It also mediates the impacts of the ENSO system on the variability of global climate (Lindzen,1994;Held,2001;Alexander et al.,2002;Li et al.,2023).In this study,we reveal that state-of-the-art reanalysis datasets may reproduce well the spatial structure of the regional HC in response to ENSO SST forcing.However,the eight reanalyses selected in this study fail to agree in terms of their representation of the amplitudes of ENSO-associated HC anomalies.Moreover,many of them (e.g.,MERRA and 20CR)may not capture well the spatial pattern of the asymmetric mode of anomalous HC.Additional measurements and analysis are needed to constrain this uncertainty,which will be a major focus in our group’s future work.

Acknowledgements.Yadi LI and Xichen LI were supported by the National Key Research and Development Program of China(Grant No.2018YFA0605703),and the National Natural Science Foundation of China (Grant Nos.42176243,41976193 and 41676190).Juan FENG was supported by National Natural Science Foundation of China (Grant No.41975079).