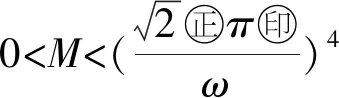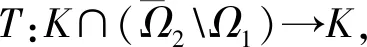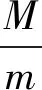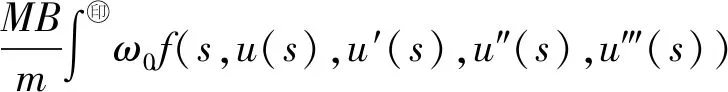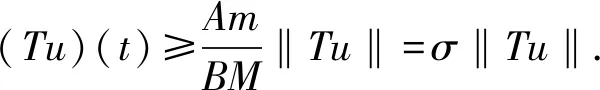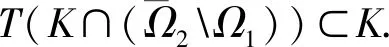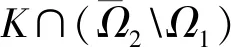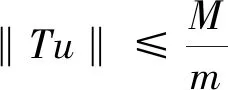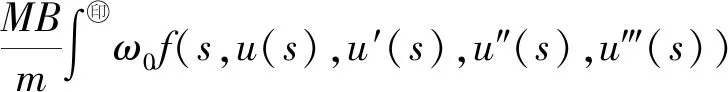一类完全非线性四阶微分方程正周期解的存在性

王晓萍, 韩晓玲

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

u(4)(t)+a(t)u(t)=f(t,u(t),u′(t),u″(t),u‴(t))

正周期解的存在性,其中,a(t)∈C([0,ω],(0,+∞)),f∈C([0,ω]×[0,+∞)×R3,[0,+∞)).在允许非线性项满足超线性增长不等式条件的情况下,利用Green函数和锥上的不动点理论,获得上述四阶微分方程正周期解的存在性结果,并通过例子验证了主要结果的有效性.

在微分方程的发展中,关于四阶微分方程周期解的研究十分活跃,它不仅在数学领域有着重要的作用,而且在物理学、生物学等领域中的应用也很广泛.许多学者对此产生兴趣并取得了一定的成果,参见文献[1-10].在讨论微分方程周期边值问题时,通常是将微分方程转化为积分方程,然后运用一些工具定理,如锥上的不动点指数定理[4,6]、Krasnoselskill不动点定理[7]、单调迭代技巧[8-9]等,把讨论解的存在性问题转化为算子不动点的存在性问题.

文献[1]考虑了四阶周期边值问题

在周期边界条件下对四阶微分算子

L4u(t)=u(4)(t)+Mu(t)

建立了极大值原理,并用极大值原理得到求解问题的上下解方法.文献[2]利用一些Sobolev常数讨论了四阶周期梁方程

其中,q(t)∈Lp(0,T),作为一个应用,得到了一类超线性梁方程周期解的唯一性.文献[3]用Schauder不动点定理,得到了四阶变系数奇异微分方程

正周期解的存在性,其中,a,b,c,d∈C(R,R+),f在原点处有奇性.文献[4]用锥上的不动点指数理论,获得了四阶变系数周期边值问题

正周期解的存在性结果,其中

a(t)∈C([0,ω],(0,+∞)).

以上文献讨论的均是非线性项f不含未知函数的导数项,对于非线性项f含有u′(t)、u″(t)、u‴(t)的完全四阶变系数微分方程,很少有人讨论.本文利用锥上的不动点理论,在非线性项满足超线性增长的不等式条件下,讨论了一类完全非线性四阶微分方程

u(4)(t)+a(t)u(t)=

f(t,u(t),u′(t),u″(t),u‴(t)),t∈[0,ω] (1)

正周期解的存在性,其中,a(t)∈C([0,ω],(0,+∞)),f∈C([0,ω]×[0,+∞)×R3,[0,+∞)).四阶微分方程用来刻画平衡状态下弹性梁的形变,只有正解在模型中才有实际应用的价值.显然,方程(1)正周期解的存在性可以通过四阶周期边值问题

(2)

正解的存在性去讨论.

下面给出本文的工具引理.

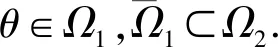
是全连续的算子,如果满足条件:

(i) ‖Tu‖≤‖u‖,u∈K∩∂Ω2;

(ii) ∃u0∈K{0}使得

u≠Tu+λu0,u∈K∩∂Ω1,λ>0,

1 预备知识

本文的空间C([0,ω])表示定义在[0,ω]上的全体连续函数在范数‖u‖C=|u(t)|下构成的Banach空间.C+([0,ω])表示在C([0,ω])上的非负连续函数,Cn([0,ω])表示定义在[0,ω]上的全体n阶连续可微函数在范数

‖u‖Cn=

下构成的Banach空间,其中n∈N.记I=[0,ω].

首先,讨论微分算子

L4u(t)=u(4)(t)+Mu(t)

在周期边界条件下满足极大值原理,其中M≠0.取空间

F4={u∈C4(I):u(i)(0)=u(i)(ω),

i=0,1,2;u‴(0)≥u‴(ω)},

若u∈F4,∀t∈I,当L4u≥0时,u≥0(u≤0).有以下引理.

引理 2[1]设M≠0,则四阶线性边值问题

存在唯一解r(t)∈C4(I),且r(t)>0于I.

引理 3[1]设M≠0,则对∀h∈C(I),四阶线性边值问题

(3)

存在唯一解u,可以表示为

其中

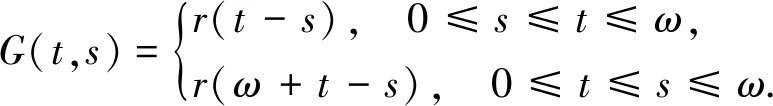
定义算子X:C(I)→C(I),

从(4)式知

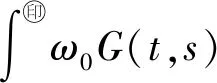
则

‖Xh‖≤ds,

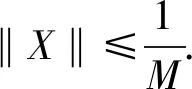
引理 4X:C(I)→C(I)是全连续算子.

证明根据G(t,s)的一致连续性,若对任给的ε>0,存在δ>0,使得对任何t1,t2∈I,只要|t1-t2|<δ,就有

其中H=则

|X(t1)-X(t2)|≤

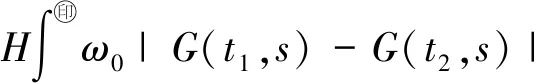
由Arzela-Ascoli定理,证得X:C(I)→C(I)是全连续算子.

记m=且

对于h(t)∈C+(I),考虑边值问题

等价于下列边值问题

定义算子

Y:C(I)→C(I),

(Yu)(t)=(M-a(t))u(t),

|(Yu)(t)|≤(M-m)|u(t)|.

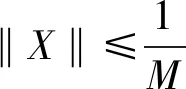
另一方面,边值问题(6)的解可以写为

u(t)=(Xh)(t)+(XYu)(t),

即Xh=(I-XY)u.由于‖XY‖<1,应用算子谱定理,有

u(t)=(I-XY)-1(Xh)(t),t∈I,

(7)

其中(I-XY)-1存在且有界.设

Q:C(I)→C(I),

(Qh)(t)=(I-XY)-1(Xh)(t),

即u(t)=(Qh)(t).显然u(t)=(Qh)(t)是边值问题(6)的解.

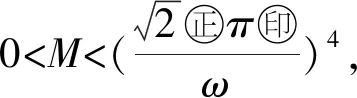
根据Neumann展式,Q表示为

Q=(I-XY)-1X=

(I+XY+(XY)2+…+(XY)n+…)X,

Q是全连续算子.当h(t)>0时,(Xh)(t)>0,可以得到

(Xh)(t)≤(Qh)(t)≤

(8)

引入以下符号:

A=

Bi=

(9)

可以看出0

定义

K={u∈C3(I):u(t)≥σ‖u‖C,

|u(i)(t)|≤liu(t),i=1,2,3,t∈R},

可知K是C3(I)中的一个锥.

2 主要结果及其证明

1) ∃θ>0,当|(a0,a1,a2,a3)|<θ时,有

f(t,a0,a1,a2,a3)≤ε(a0+|a1|+|a2|+|a3|),

a0≥0,t∈I,

其中,ε>0满足MBωε(1+l1+l2+l3)

2) ∃μ>0,当|(a0,a1,a2,a3)|>μ时,有

f(t,a0,a1,a2,a3)≥ηa0,a0≥0,t∈I,

其中,η>0满足Aωησ>1.

那么,方程(1)至少有一个正的ω-周期解.

(Tu)(t)=Q(f(t,u(t),u′(t),u″(t),u‴(t)),

可以看出Tu=u的一个不动点就是方程(1)的一个解.定义2个开子集:

Ω1={u∈C3(I):‖u‖

Ω2={u∈C3(I):‖u‖

其中,r、R是2个常数且R>r>0.

r

结合(8)和(9)式有

(Tu)(t)≥

和

‖Tu‖≤

f(s,u(s),u′(s),u″(s),u‴(s))ds|≤

f(s,u(s),u′(s),u″(s),u‴(s))ds≤

lds≤

lds≤

li(Tu)(t),i=1,2,3.

|(u(t),u′(t),u″(t),u‴(t))|=

由条件1)有

f(t,u(t),u′(t),u″(t),u‴(t))≤

ε(u(t)+|u′(t)|+|u″(t)|+|u‴(t)|).

根据(8)和(9)式有

f(s,u(s),u′(s),u″(s),u‴(s))ds≤

除此之外,可得

f(s,u(s),u′(s),u″(s),u‴(s))ds|≤

f(s,u(s),u′(s),u″(s),u‴(s))ds≤

接下来证明

‖Tu‖≤‖u‖,u∈K∩∂Ω2.

(10)

|(u(t),u′(t),u″(t),u‴(t))|=

所以由条件1)可得

f(t,u(t),u′(t),u″(t),u‴(t))≤

ε(u(t)+|u′(t)|+|u″(t)|+|u‴(t)|).

结合(8)和(9)式得到

f(s,u(s),u′(s),u″(s),u‴(s))ds≤

由条件1)可得

故(10)式成立.

另一方面,设u0=1,u0∈K{0}.现在证明

u≠Tu+λu0,u∈K∩∂Ω1,λ>0.

(11)

如果不是,则存在u1∈K∩∂Ω1,λ0>0,使得

u1=Tu1+λ0u0.

|u1(t)|≥σr>μ.

所以由条件2)可得

根据条件2)、(8)和(9)式有

u1=Tu1+λ0u0≥

这与u1≤r矛盾,故(11)式得证.

例 1考虑下列完全非线性四阶微分方程

u(4)(t)+(2+cos2t)u(t)=

x2(u″(t))2+x3(u‴(t))2),t∈[0,π], (12)

与方程(1)对比,易知a(t)=2+cos2t,ω=π,01,i=0,1,2,3,则非线性项

x1(u′(t))2+x2(u″(t))2+x3(u‴(t))2)

满足条件1)和2).由定理1知,方程(12)至少有一个正的π-周期解.