时间序列模型在经济分析中的应用——陕西省GDP分析与预测

谢妮妮

（西安财经大学行知学院经济与统计学院,陕西 西安 710038）

时间序列分析最早诞生于7 000年前的古埃及。到20世纪末[1]，数学家詹金斯（Jenkins）和博克思（Box）建立并提出了ARIMA模型，即自回归积分滑动平均模型（Autoregressive Integrated Moving Average Model，以下简称ARIMA），时间序列分析得到进一步完善，并被更广泛应用。近年来，越来越多的国内外学者采用时间序列分析法对不同地区的GDP进行研究，探索并寻找发展变化规律，利用对未来事物的发展状况或趋势进行有关预测。例如，在商业领域可以用于预测股票及基金的趋势，进行炒股及基金理财等；在农业领域可以用于研究农作物价格及产量的变化，增加收益等；在自然领域可以用于预测天气变化及温度的变化等；在社会领域可以用研究出生率、死亡率及犯罪率等。所以，时间序列分析的预测作用在实际生活中具有极其重要的作用。

GDP可以显著反映区域经济发展情况，GDP是衡量经济生活甚至社会生活的重要指标和核心尺度之一。GDP为政府对宏观经济发展状况进行战略制定和对经济政策进行制定时提供了极其重要的参考依据，而且对宏观经济健康平稳发展起到导向作用，还可以利用其研究结果对经济发展趋势进行精准预测，从而更好促进经济和社会发展。所以，对GDP进行深入的研究具有极其重要的实际价值和参考意义。

1 时间序列的相关定义及统计方法的选择

时间序列分析法的研究对象是动态数据，通过借助统计分析等方法，探寻随机数列所遵循的统计规律，对已经获得的历史数据进行分析及预测，从而解决实际问题。

2 统计分析过程及研究

从陕西省统计局发布的《陕西七十年》和《陕西统计年鉴》中，选取1952—2019年陕西省GDP数据并对其进行分析。确定模型之前，先利用EXCEL对GDP序列进行趋势分析。如图1所示。

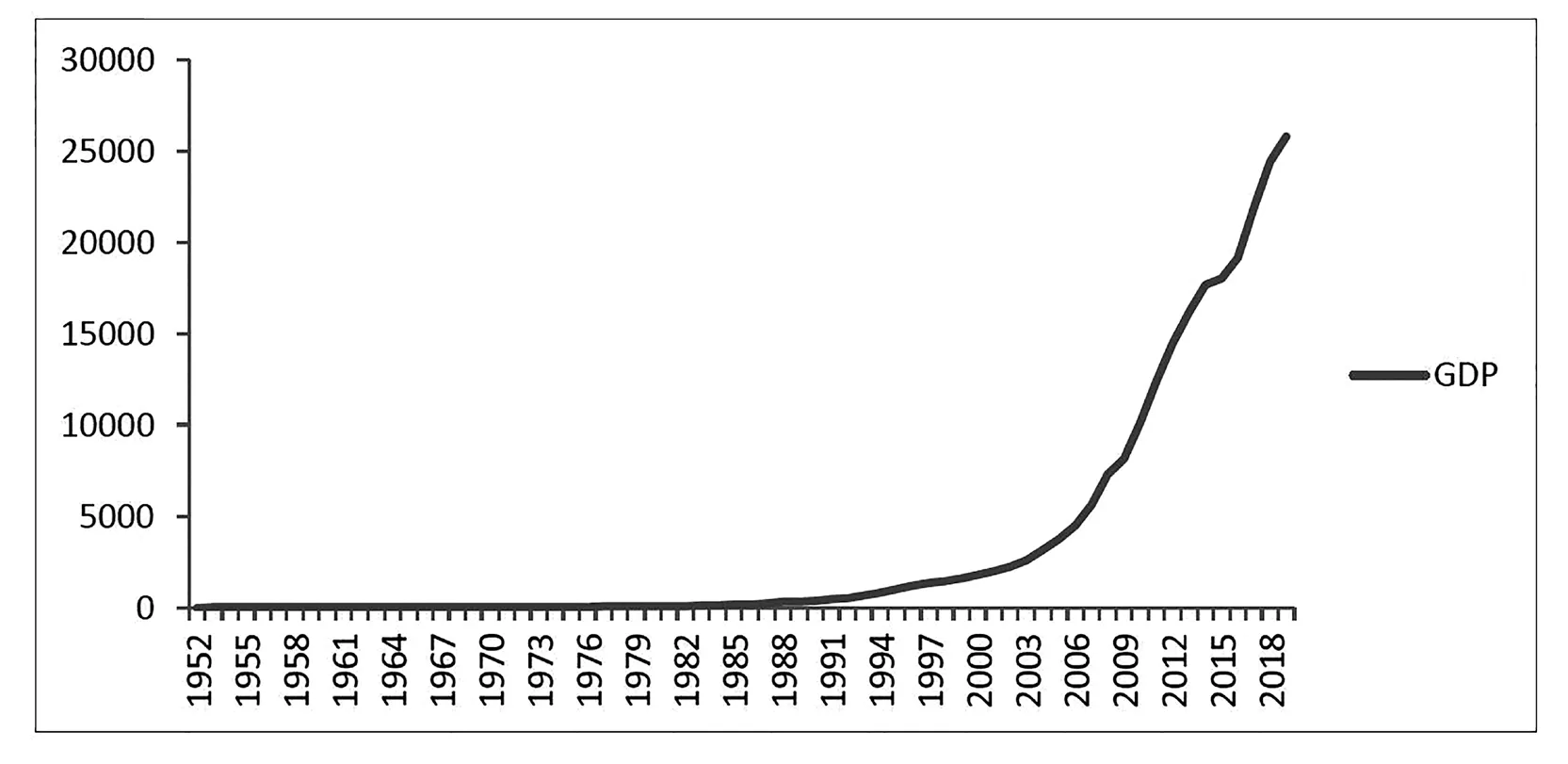
图1 陕西省GDP(生产总值(亿元))折线图

由图2可得，陕西省GDP具有明显的指数增长趋势，可以观察得出该时间序列为非平稳序列。陕西省GDP的变化趋势与指数趋势拟合，所以选用指数函数来拟合陕西省GDP(亿元)。

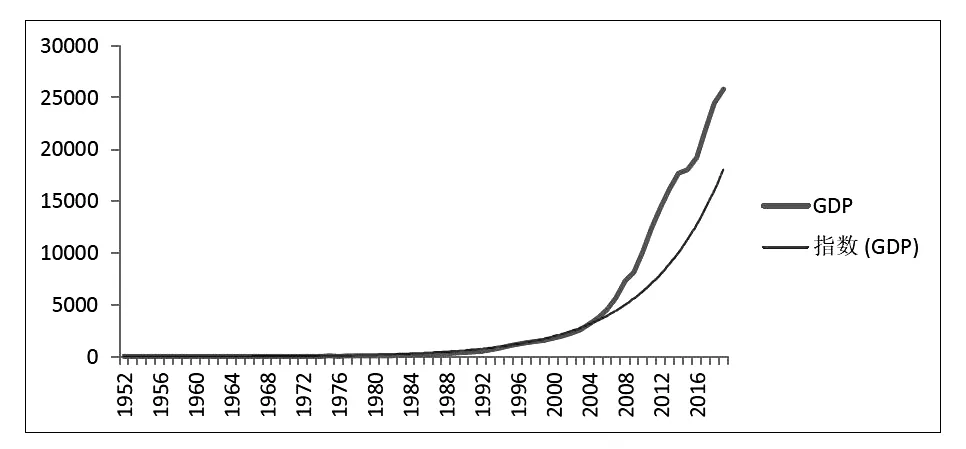
图2 陕西省GDP(生产总值(亿元))指数趋势拟合图

2.1 ARIMA分析过程概述

ARIMA(p,d,q)[2]中，AR为“自回归”，p是自回归项数[3]；MA是“滑动平均”[4]，q是滑动平均项数[5]，d是使之成为平稳序列所做的差分次数（阶数）[6]。ARIMA模型可以表示为[7]：

其中L是滞后算子，d∈Z,d＞0。非平稳时间序列经过差分处理后可以转换为平稳时间序列，其中差分的次数就是齐次的阶。

将∇记为差分算子，那么有

对于延迟算子B，有

因此可以得出

设有d阶其次非平稳时间序列yt，那么有∇dyt是平稳时间序列，则可以设其为ARMA(p,q)模型，即

其中λ(B)= 1-λ1B-λ2B2-…-λPBP，分别为自回归系数多项式和滑动平均系数多项式。为零均值白噪声序列。可记为ARIMA(p,d,q)。

2.1.1 模型识别相关概述

由图3时间序列趋势折线图可知，随着时间推移，序列季节波动几乎接近平滑，越来越小，所以该时间序列季节成分不显著。由于ARIMA模型要求序列是平稳的，所以对GDP数据序列进行一阶拆分，由其结果可知，陕西省GDP序列在零比线两侧的时间跨度为平均差，因此认为是稳定的。对拆分后的GDP时间序列进行ACF（自相关）和PACF（偏自相关）分析可得，自相关呈现逐渐衰减的趋势，由此可知自相关拖尾；偏自相关呈断落式下跌，由此可知偏自相关截尾。

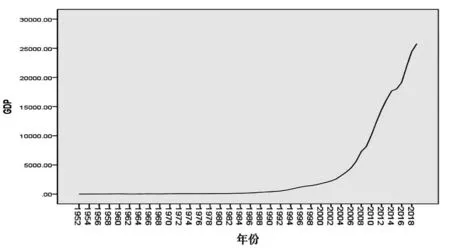
图3 陕西省GDP(生产总值(亿元))时间序列趋势图

2.1.2 模型检查和相关分析

ARIMA模型结果为：

如表1、表2、表3所示，决定系数R2越接近于1，模型效果拟合越好，由于R2=0.998，所以拟合效果非常好，AR和MA的系数分别是0.527和-0.415，有效性在0.01以下，系数不是0。综上可认为，该模型拟合效果很好。通过时间序列趋势折线图、ACF和PACF分析等可知序列是平稳的。综上所述ARIMA(1,2,1)是合理的。

表1 模型描述

表2 模型统计量

表3 ARIMA 模型参数

2.1.3 模型预测及相关分析研究

因此，ARIMA模型结果为：

最后，使用上述模型对陕西省GDP时间序列进行拟合预测，通过模拟实验发现，上述模型拟合效果很好。由大量模拟实验可得，目前使用ARIMA（3,1,3）模型预测了2019年陕西省GDP的自然对数。2019年至2021年的预测结果见表4。

表4 ARIMA模型预测结果

表5 输入/移去的变量b

2.1.4 模型的回归分析

对陕西省GDP及第一、二、三产业的相关数据通过SPSS进行研究分析，结果如下所示：

如上表6所示，模型适应系数（包括第一、第二和第三产业的三个变量）的调整判定系数为1.000。Durbin-Watson测试的结果是1.487，说明因变量的取值不存在序列相关。

表6 模型汇总b

表7显示，模型的有效性水平为0.000，与回归模型合作有意义。但是，无效变量被删除时，F会增加。这表明仅包括第一，第二，第三产业的三个变量的模型的适应性最好。

表7 Anova b

如果模型的容量极限小于0.1并且色散扩大系数大于10，则存在变量之间的多共线性。因此，从表8可以得出结论，三个独立变量没有多重共线性。GDP与第一、第二、第三产业有着积极的关系。所以，有回归系数表可得回归模型为：

表8 系数a

其中，y是GDP，x1是第一产业，x2是第二产业，x3是第三产业。

3 结语

本研究通过对1952—2019年陕西省的GDP时间序列数据进行大量拟合实验，并经研究分析可知，由于一个时间序列与其ACF及PACF存在错综复杂的关系，所以对时间序列进行建模，以及识别时间序列模型并非易事，需要对时间序列进行大量实验并结合实验结果进行研究分析，才能得到理想的结果，从而更好地判别和选择最优模型。首先，对1952—2019年陕西省的GDP时间序列进行研究，然后建立了ARIMA（1，2，1）模型，最后通过对时间序列模型参数的变换，生成了残差序列中的白噪声序列。其次，通过对1952—2019年陕西省的GDP时间序列建模结果进行分析研究，发现运用SPSS软件建立的时间序列模型的拟合效果更具有实际价值，也更有可信性，所以可利用该模型对2011—2019年的陕西省GDP进行预测，同时将相对误差控制在5%之内，可以得出较为准确的结果，从而更好地预测未来几年陕西省GDP的发展情况，有助于促进经济发展。最后，从GDP变化的角度对经济预测进行了分析，提高了经济预测的准确性和实际价值，本研究可以为国家宏观经济政策和发展战略的调整、宏观经济平稳健康发展，以及人口变化和宏观经济指标的调整等提供参考依据，可以有效规避一些经济活动中隐藏的风险，从而更好促进陕西省以及我国经济健康发展。