基于电磁混合耦合的SIW 宽阻带带通滤波器设计*

周为荣，周 鹤，孟 涛，李帅合，魏志杰

（1.中通服咨询设计研究院有限公司，江苏 南京 210019；2.南京信息工程大学，江苏 南京 210044）

0 引言

随着无线移动通信技术的迅速发展，无线电发射机和雷达产生的谐波、杂散电磁辐射增强，这些干扰杂波信号时刻影响着设备系统运行，会导致设备失控、雷达天线跟踪位置产生误差及移动通话质量不稳定等问题[1-3]。这极大地推动了具有频率选择和抑制谐波信号等功能的微波滤波器的发展[4-6]。以基片集成波导带通滤波器为代表的微波滤波器因具有造价低、损耗小、重量轻、品质因数高且易于集成等优点得到广泛关注[7-9]。然而，随着电磁环境日益复杂，对移动通信系统正常运行的干扰日益严重，为了减少这些干扰的影响以提高通信信号质量，研究者们提出了多种宽阻带带通滤波器的实现方法。

文献[10]利用基片集成波导（Substrate Integrated Waveguide，SIW）的高通传输特性和补偿型微带谐振单元（Compensated Compacrt Microstrip Resonant Cell，CMRC）的低通传输特性，实现了带通滤波器的宽阻带性能，但阻带拓宽的范围有限。文献[11]将缺陷地结构（Defected Ground Structure，DGS）的带阻谐振器产生的传输零点放置在某谐波信号的谐振频率处，来达到抑制效果，但增加了整个电路的复杂性，后续的不可控因素也会增多。文献[12]通过偏移馈电端口的方式来修正模式的正交性，仅获得了2f0阻带，延伸范围明显不足。文献[13]介绍了一种多层结构中全新的设计方法，将耦合槽移离腔体侧壁约1/6 处，并固定耦合槽宽度，通过控制耦合槽长度来控制耦合强度，能有效地抑制TE404以下所有高次模。但该滤波器输入端和输出端不在同一平面，因此不易与平面电路集成。

上述文献设计的滤波器无法兼顾设计方法简单、阻带范围宽和易于集成等特点。因此，本文结合模式的电磁分布特性，提出了基于电磁混合耦合的SIW 宽阻带带通滤波器。首先，在多层结构的SIW 滤波器中，运用模式的本征抑制方法来抑制对称分布的TEm0n（m=2,4,6,…）和TEm0n（n=2,4,6,…）模的谐波通带。其次，基于电磁混合耦合理论，在中间金属层上刻蚀出两组不对称的耦合圆孔来分别抑制TE103和TE301及TE303模的谐波通带。最后，仿真并实测了该滤波器，显示两者吻合度较好，验证了该设计方法的可行性和准确性。

1 电磁混合耦合理论

一般情况下，绝大多数滤波器是同步调谐滤波器，即谐振腔间没有耦合时，谐振频率是一样的。因此，同步调谐滤波器中，在谐振腔是对称耦合的情况下，若两个谐振腔的耦合中同时存在电耦合和磁耦合，总的耦合系数kall可以表示为[14]：

式中：km为磁场耦合系数，ke为电场耦合系数。由式（1）可知，存在电耦合、磁耦合、电磁混合耦合这3 种耦合方式。当模式引入的电耦合量ke大于磁耦合量km时，该模式为电耦合，即电场传输能量；当模式引入的电耦合量ke小于磁耦合量km时，该模式为磁耦合，即磁场传输能量；当模式引入的电耦合量ke等于磁耦合量km时，总的耦合系数kall约为零，该模式为电磁混合耦合，即可抑制该模式的能量耦合。

2 非完全对称式的SIW 带通滤波器设计

在SIW 方形谐振腔中，随着频率的逐渐升高，存在的模式依次为：TE101、TE102和TE201、TE202、TE103和TE301、TE203和TE302、TE104和TE401、TE303、TE204和TE402、TE304和TE403、TE105和TE501……根据模式的排列顺序，得到频率比设计公式为：

由公式（2），得：

由式（3）至式（6）易知，高次模TE102和TE201、TE202、TE301和TE103及TE303接近于主通带，严重降低了滤波器的宽阻带性能。因此，为了抑制这些高次模的谐振耦合，本小节将基于电磁混合耦合理论，结合模式的本征抑制，提出非完全对称式的电磁混合耦合四阶SIW 宽阻带带通滤波器。

2.1 模式的本征抑制

如图1 所示，将外部馈电端口和内部耦合窗口设置在箭头A、B 的指向，可以有效地抑制TE102和TE201、TE202、TE203和TE302、TE104和TE401、TE204和TE402、TE304和TE403等模的谐振耦合[15]，但无法抑制TE103和TE301及TE303模的谐振耦合，因此，需要引入电磁混合耦合理论，使得TE103和TE301及TE303模的耦合系数趋于零，从而TE103和TE301及TE303模将得到很好的抑制。

图1 SIW 谐振腔前几个模式的电场幅度分布

2.2 模式的电磁特性分析

2.2.1 TE103/TE301 和TE101 模

如图2 所示，阵列由1 个位于腔体中心、半径为r1的圆形耦合通孔和4 个距离腔体中心为d、半径为r11的圆形耦合通孔组成。基于耦合圆孔阵列TE103/TE301模的电磁分布特性可知，设计对称分布的半径为r11的耦合圆孔有着巧妙之处，即上下耦合的圆孔对于TE103模，能够提供电耦合去抵消磁耦合，而对于TE301模，能够提供磁耦合去抵消电耦合；左右耦合的圆孔对于TE103模，能够提供磁耦合去抵消电耦合，而对于TE301模，能够提供电耦合去抵消磁耦合。当取合适的r1，r11和d时，耦合圆孔引入TE301模的磁耦合量等于电耦合量，由式（1）易知，TE301模的总耦合系数为零，实现了对TE301模的抑制。由于两个高次模正交分布于腔体中，而设计的耦合圆孔也是正交分布，因此当TE301模的耦合被抑制时，TE103模也随之被抑制[16]。如图3 所示，设置的半径为r11的耦合圆孔应尽量远离主模TE101的磁场最强处，可减小对工作模式TE101电耦合的削弱作用。

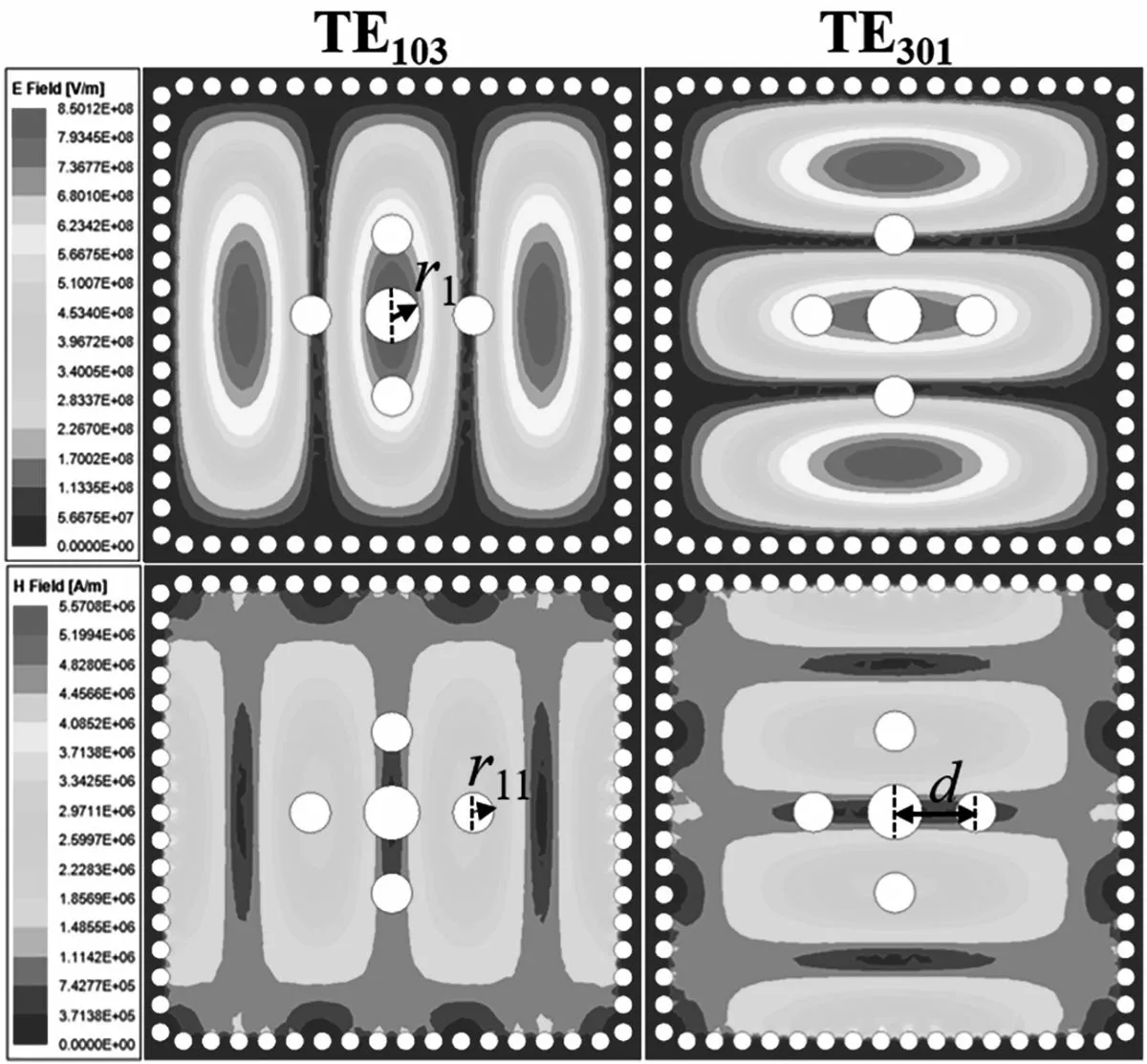
图2 含有耦合圆孔TE103 和TE301 模的电磁场幅度分布

图3 含有耦合圆孔TE101 模的电磁场幅度分布

2.2.2 TE303 和TE101 模

如图4 所示，阵列由5 个耦合圆孔组成，其中一个耦合圆孔位于腔体中心，半径为r2，其他4 个耦合圆孔位于对角线上并对称分布，且距腔体中心的距离为，半径为r22。由图4 可知，半径为r2的中心耦合圆孔提供TE303模的电耦合，4个斜对角线上半径为r22的圆形耦合孔径提供TE303模的磁耦合。当取合适的r2，r22和d1时，使得耦合圆孔引入TE303模的磁耦合量等于电耦合量，由式（1）知，TE303模的总耦合系数为零，实现对TE303模的抑制。

图4 含有耦合圆孔TE303 模的电磁场幅度分布

同样值得关注的是，当抑制TE303模的耦合时，设置的半径为r22的耦合圆孔也应远离主模TE101的磁场最强处。如图5 所示，当中心耦合圆孔r2位于主模TE101电场最强处时，主模TE101采用电耦合的方式传输能量，与绝大多数设计的滤波器的主模采用磁耦合方式不同。半径为r22的耦合圆孔均分布于TE101磁场最弱处，由式（1）知，可减小对工作模式TE101电耦合的削弱作用。

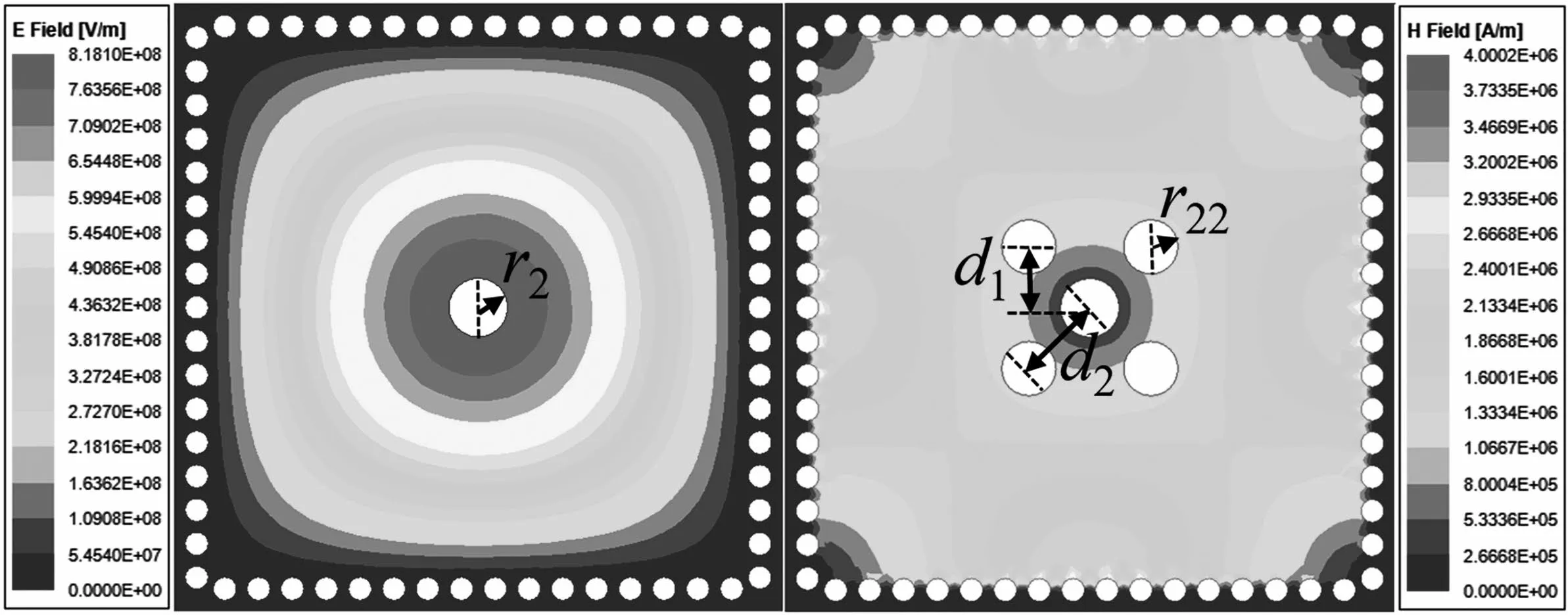
图5 含有耦合圆孔TE101 模的电磁场幅度分布

在实际耦合时，由于SIW 腔体中模式的电磁场分布与理想情况下稍有不同，并且根据模式的电磁场分布特性，只能初步得到耦合圆孔分布情况，想要更加精确地耦合圆孔（r1，r2，r11，r22）及间距（d，d1）的大小，还需要借助仿真软件HFSS 来提取模式的耦合系数得到确定的实际耦合位置。

2.3 模式的耦合系数分析

为了进一步确保提取TE103和TE301及TE303模的耦合系数的准确性，以及验证电磁混合耦合方法的可行性，通过以下两种情形提取TE103和TE301及TE303模的耦合系数进行分析对比。

2.3.1 情形1：选取d 和d1 作为自变量

首先，提取TE103和TE301模的耦合系数，如图6（a）和图6（b）所示。选取r1为1.5 mm，随着r11的不断增大，TE103和TE301模的耦合系数最小值点对应于更小的d。换言之，随着r11的不断增大，适当地减小d值可以获得对TE103和TE301模的抑制，并且两组耦合系数呈现类似的变化（即两组耦合系数达到最小值时，d几乎在相同的位置）。另外，提取了主模TE101模的耦合系数，如图6（c）所示。结合图6（a）中TE103和TE301模的耦合系数分析，确保主模耦合性能好的同时，取r11为1.2 mm，d在[4.2,4.6]mm 范围内时，均能抑制TE103和TE301模的谐振耦合。

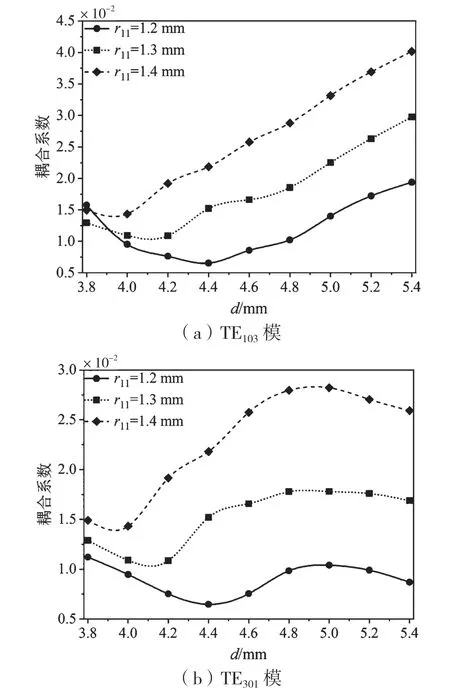
图6 随d 变化的TE103 和TE301 及TE101 模的耦合系数

其次，提取TE303模的耦合系数，如图7 所示。固定r2为1.3 mm，随着r22的不断增大，TE303模的耦合系数最小值点对应于更大的d1。因此，适当地增大d1值可以获得对TE303模的抑制。另外，也提取了主模TE101模的耦合系数，并结合TE303模的耦合系数分析，保证主模耦合性能的同时，取r22为1.2 mm，d1为[2.8,3.2]mm 范围内时，均能抑制TE303模。

图7 随d1 变化的TE303 和TE101 模的耦合系数

2.3.2 情形2：选取r11 和r22 作为自变量

首先，提取TE103/TE301模的耦合系数，如图8所示。固定r1为1.5mm，随着d不断增大，TE103/TE301模的耦合系数最小值点对应于更小的r11，因此，适当地减小r11值可以获得对TE103/TE301模的抑制，并且两组耦合系数呈现类似的变化。同理，可得TE303模的耦合系数，如图9 所示。固定r2为1.3 mm，随着d1不断增大，TE303模的耦合系数最小值点对应于更大的r22。因此，适当地增大r22值可以获得对TE303模的抑制。

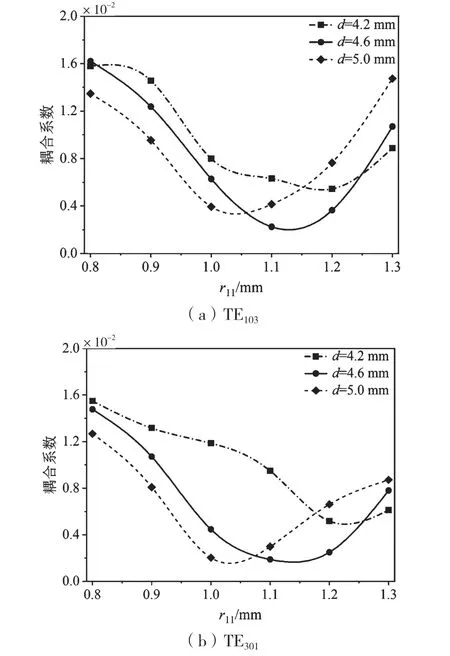
图8 随r11 变化的TE103 和TE301 模的耦合系数

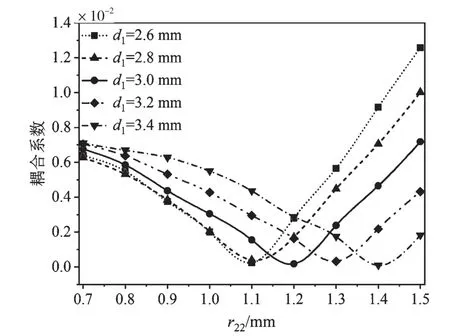
图9 随r22 变化的TE303 模的耦合系数

总之，选取耦合间距d和耦合孔径r11分别作为自变量时，提取TE103/TE301模的耦合系数呈现的规律一致，即抑制TE103/TE301高次模的谐振耦合时，通过提取耦合系数发现，在一定范围内，为了获得更小的TE103/TE301的耦合量，r11与d呈负相关；选取耦合间距d1和耦合孔径r22分别作为自变量时，提取TE303模的耦合系数的规律相同，即抑制TE303高次模的谐振耦合时，通过提取耦合系数发现，在一定范围内，为了获得更小的TE303的耦合量，r22与d1呈正相关。

2.4 结构设计与分析

基于上述详细的设计方法，提出非完全对称式的四阶SIW 滤波器，其结构如图10 所示，相关参数如表1 所示。该多层结构从上往下依次堆叠的是顶层金属层、介质基板1、中间金属层、介质基板2 和底层金属层。中间金属层R2 谐振腔中内部耦合圆孔阵列包括半径为r1的中心耦合圆孔和两对半径为r11的耦合圆孔，一对半径为r11的耦合圆孔设置在半径为r1的中心耦合圆孔上、下侧，另一对半径为r11的耦合圆孔设置在半径为r1的中心耦合圆孔的左、右侧，所有半径为r11的耦合圆孔与半径为r1的中心耦合圆孔的距离d一致。中间金属层R3 的谐振腔中内部耦合孔阵列包括半径为r2的中心耦合圆孔和两对半径为r22的耦合圆孔，一对半径为r22的耦合圆孔设置在半径为r2的中心耦合圆孔的斜对角方向上，呈45°且两侧对称分布，并且位于半径为r2的中心耦合圆孔的两侧，另一对半径为r22的耦合圆孔设置在半径为r2的中心耦合圆孔的斜对角方向上，呈135°且两侧对称分布，并且位于半径为r2的中心耦合圆孔的两侧，所有半径为r22的耦合圆孔与半径为r2的中心耦合圆孔的距离一致[17]。

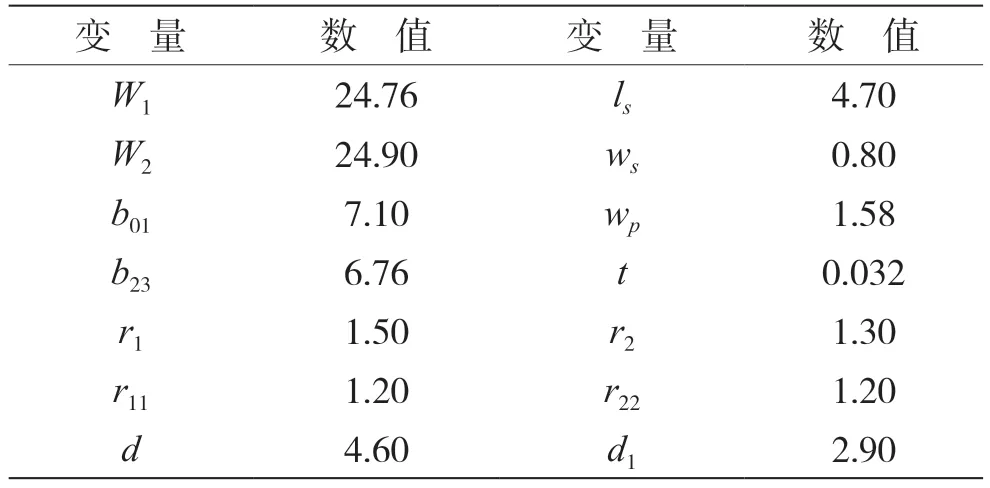
表1 二阶SIW 宽阻带滤波器的结构参数/mm

图10 非完全对称式的四阶SIW 滤波器平面结构

图11 展示的是根据图6 和图7 中选用d为[4.2,4.6]mm 和d1为[2.8,3.2]mm 作为设计参数时所仿真的S21。当r11=1.2 mm，d=4.6 mm 时，抑制了TE103/TE301模的谐振耦合，且带外抑制优于21 dB；当r22=1.2 mm，d1=3 mm 时，抑制了TE303模的谐振耦合，且带外抑制优于30 dB。

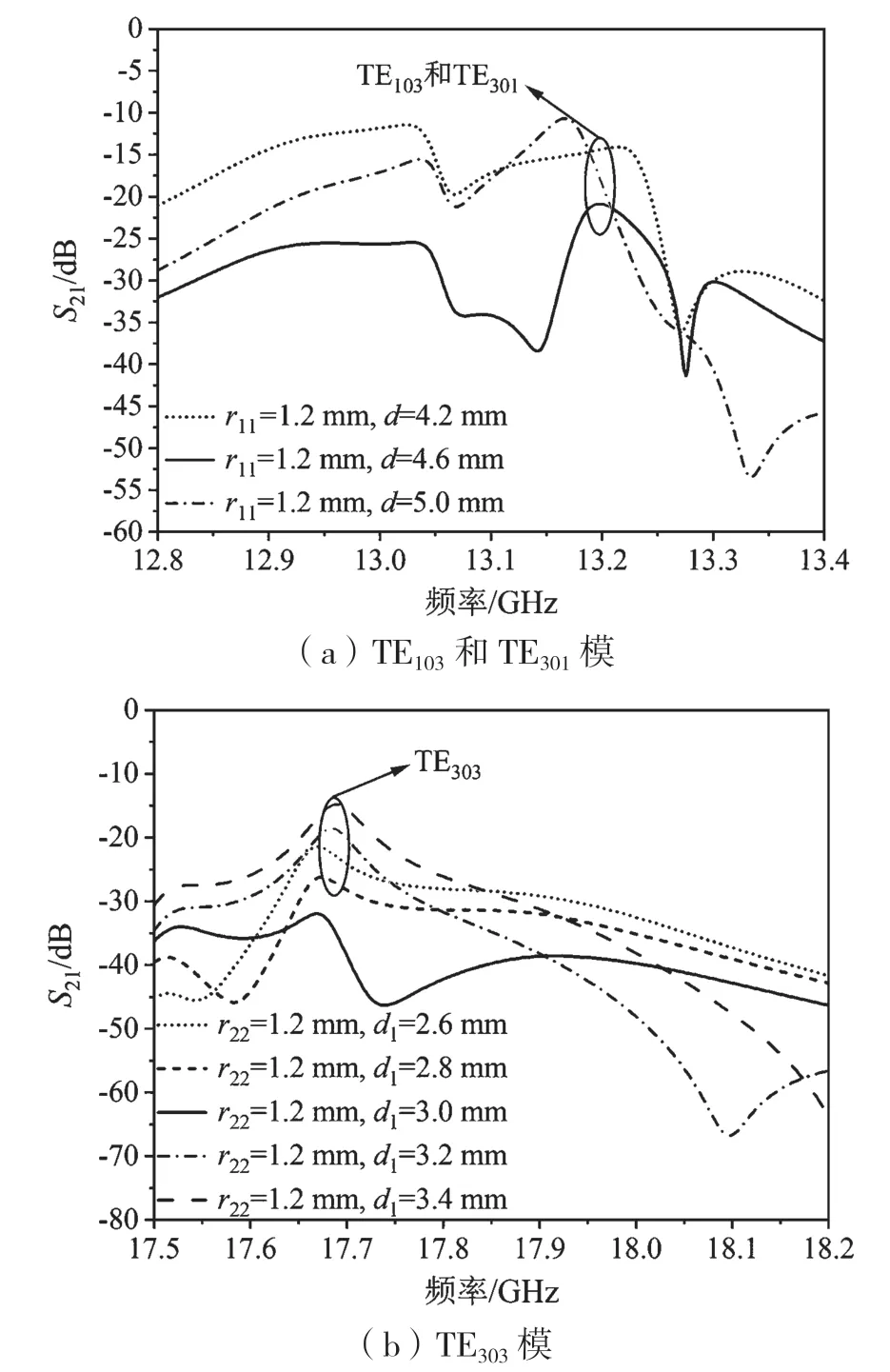
图11 随d 和d1 变化的仿真S21

2.5 仿真与实测分析

图12 展示的是该滤波器的实物平面展开，两组互不对称的耦合圆孔阵列均刻蚀在中间金属层上，但每一组中的耦合圆孔阵列是对称分布的。滤波器的实测图以及仿真和实测的S参数如图13 所示，通过焊接SMA 接头在输入、输出端连接安捷伦E8363C 的网络矢量分析仪进行测量。测得通带内中心频率f0为5.94 GHz，相对带宽为2.44%，实测的插入损耗为-3.46 dB，其损耗增加可能来源于SMA 接头自身的损耗、焊接带来的损耗、转换接头的损耗、实物加工工艺精度带来的损耗、网络矢量分析仪校准不精确这5 个方面。但无论仿真还是实测的结果，滤波器优于20 dB 的阻带一直可以延伸至3.85f0。仿真和实测结果显示两者吻合度基本相同。

图13 SIW 滤波器的仿真和实测的S 参数

图14 展示的是由仿真软件HFSS 提取滤波器的外部品质因数Qe与端口的开口深度ls和开口宽度ws之间的关系。随着ws和ls的不断增大，Qe却不断减小。选取ws=0.8 mm 和ls=4.7 mm，得Qe≈42，因此，该滤波器拥有较高的外部品质因数。图15 展示的是，与经典四阶SIW 滤波器相比较，当非完全对称式的四阶SIW 滤波器拥有相同的带宽和插入损耗时，尺寸缩小了一半。因此，基于多层结构的滤波器更有利于系统的集成化和小型化。表2 为本文提出的宽阻带滤波器与已经实现的宽阻带滤波器实例的对比结果。由表2 可知，本文所提宽阻带滤波器通过简单的设计方法，实现了滤波器阻带的进一步延伸，并且多层层叠的方式还可以保持紧凑的结构，有利于更好地集成到通信电路系统中。

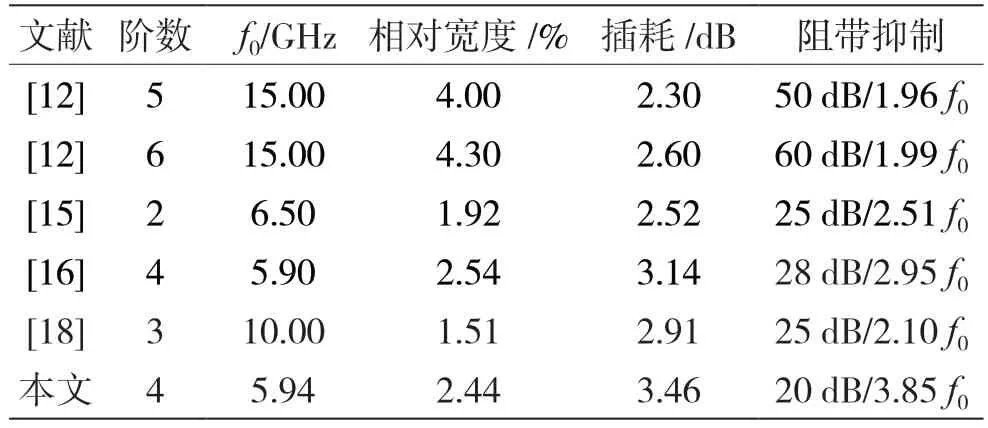
表2 滤波器性能参数对比

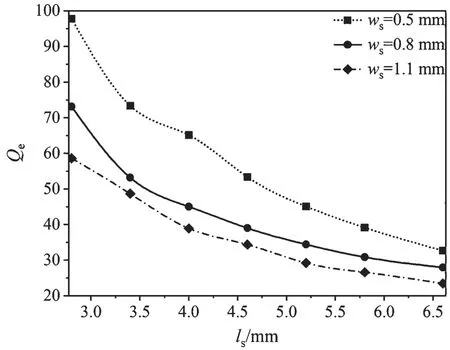
图14 Qe 与ls 和ws 的关系曲线

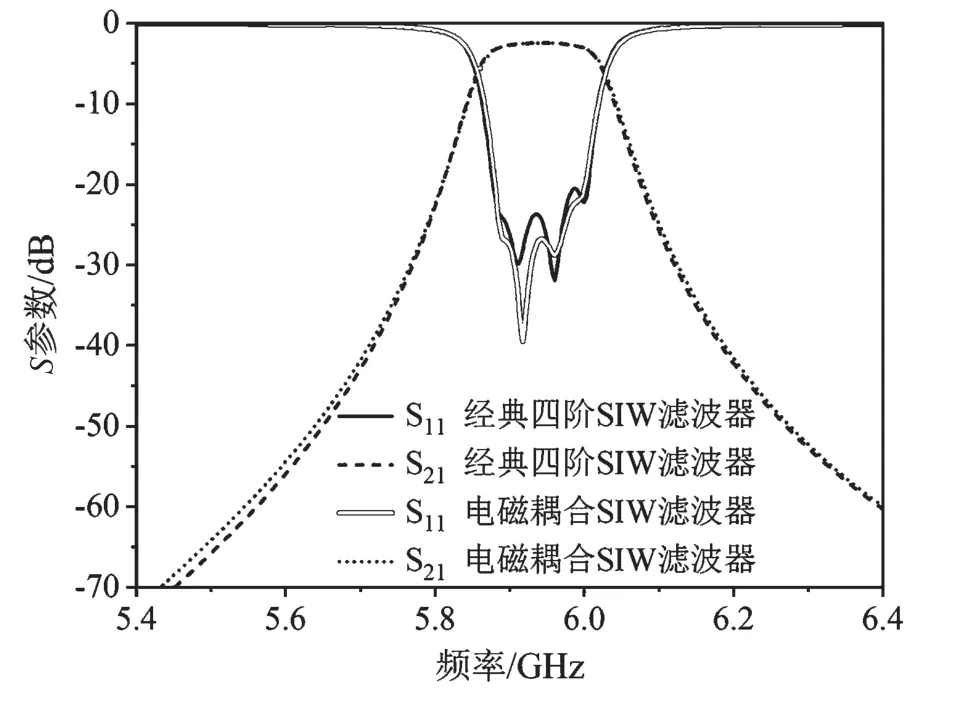
图15 滤波器的传输通带响应

3 结语

本文基于多层结构，利用模式的本征抑制和电磁混合耦合理论，设计并实测了非对称式的四阶SIW 滤波器。详细阐述并验证了设计方法，仿真和实测结果均显示，滤波器的阻带宽度延伸至3.85f0时，抑制深度均优于20 dB，验证了该设计方法的准确性和可行性，也为今后基于电磁混合耦合方法设计SIW 宽阻带滤波器提供了思路。