顾及大气剖面的GPT3改进模型及其精度评价

王 顺

1 上海勘测设计研究院有限公司,上海市逸仙路388号,200434

对流层延迟是无线电空间大地测量技术的重要误差源,通常结合天顶方向对流层延迟ZTD和映射函数实现传播路径的对流层延迟改正,因此精确获取ZTD是提高对流层延迟改正精度的关键。目前获取ZTD最常用的方法是模型法,主要根据大气折射率与气压、温度和水汽的关系建立计算方程。通常将与水汽相关的部分称为天顶湿延迟(zenith wet delay, ZWD),将不相关部分称为天顶干延迟(zenith hydrostatic delay, ZHD),也称天顶静力学延迟。

早期ZTD模型主要有Saastamoinen模型[1]和Hopfield模型[2],但二者均需要实测气象数据,模型应用具有一定的局限性。随后出现了以气象参数经验模型为数据源的对流层延迟模型,可将气象参数模型化,用户只需输入测站位置和时间,即可得到站点的对流层延迟值,其中UNB3m和GPT3模型最具代表性。Collins等将UNB3模型中的水汽压替换为相对湿度得到UNB3m[3],包含气压、温度、相对湿度、温度递减率和水汽直减因子5个气象参数,并以查询表的方式存储上述气象参数的年均值和年变化值。该模型气象参数较少、计算方法简单,被广泛应用于卫星导航领域。GPT3模型则是Landskron等[4]在GPT2w模型[5]基础上增加映射函数系数和水平梯度参数所建立的新模型,包含气压、温度、比湿、大气加权平均温度、温度递减率、水汽直减因子等14个参数,并以1°×1°或5°×5°的网格形式存储各参数的年均值、年变化值和半年变化值,精度较高且开源,是目前的研究热点。国内外学者围绕GPT3模型的精度开展研究,都证明了GPT3模型在地表层具有高精度和稳定性,但其在大气廓线预报上存在不足[6-9]。

基于此,本文基于已有研究成果,在深入分析GPT3模型垂直改正方法的基础上提出一种顾及大气剖面的GPT3改进模型GPT3v,利用探空数据、NCEP再分析资料以及GNSS ZTD数据对改进后的模型进行精度验证。结果表明,与GPT3模型相比,GPT3v模型在垂直方向上的预报精度显著提高。

1 GPT3模型的垂直修正方法分析与改进

1.1 GPT3模型的垂直修正方法

水平方向上GPT3模型各气象参数的计算方法可参考文献[4],本文重点关注各参数在垂直高度上的改正方法。GPT3模型计算测站点温度T、气压P和水汽压e的垂直修正公式如下:

T=T0+dT·dh

(1)

(2)

(3)

式中,T0、P0和e0分别为格网点高度上的温度、气压和水汽压,其中e0由比湿Q和P0计算得到:e0=Q·P0/(0.622+0.378Q);dT为温度递减率;dh为测站与网格点的高度差;gm=9.806 65 m/s2;dMtr=28.965×10-3kg/mol;Rg=8.314 3 J/K·mol;Tv为虚温,由格网点T0和Q计算得到,即Tv=T0·(1+0.607 7Q);λ为水汽直减因子。测站的对流层延迟改正是利用Saastamoinen和Askne&Nordius模型分别对ZHD和ZWD进行计算:

ZHD=

(4)

(5)

式中,lat为测站纬度,H为测站大地高,Rd=287.054J/kg·K,Tm为加权平均温度,k2=16.48 K/hPa,k3=3.776×105K/hPa。

1.2 垂直修正方法改进

由GPT3模型的垂直修正方法可知,温度廓线估计的关键在于温度递减率是否正确。首先利用2021年516个全球探空站数据计算得到的温度递减率(由站点上方温度廓线经线性拟合得到,截止高度为11 km)作为参考值,分析GPT3模型温度递减率的精度,并与UNB3m模型进行比较,统计结果见表1(单位K/km)和图1。

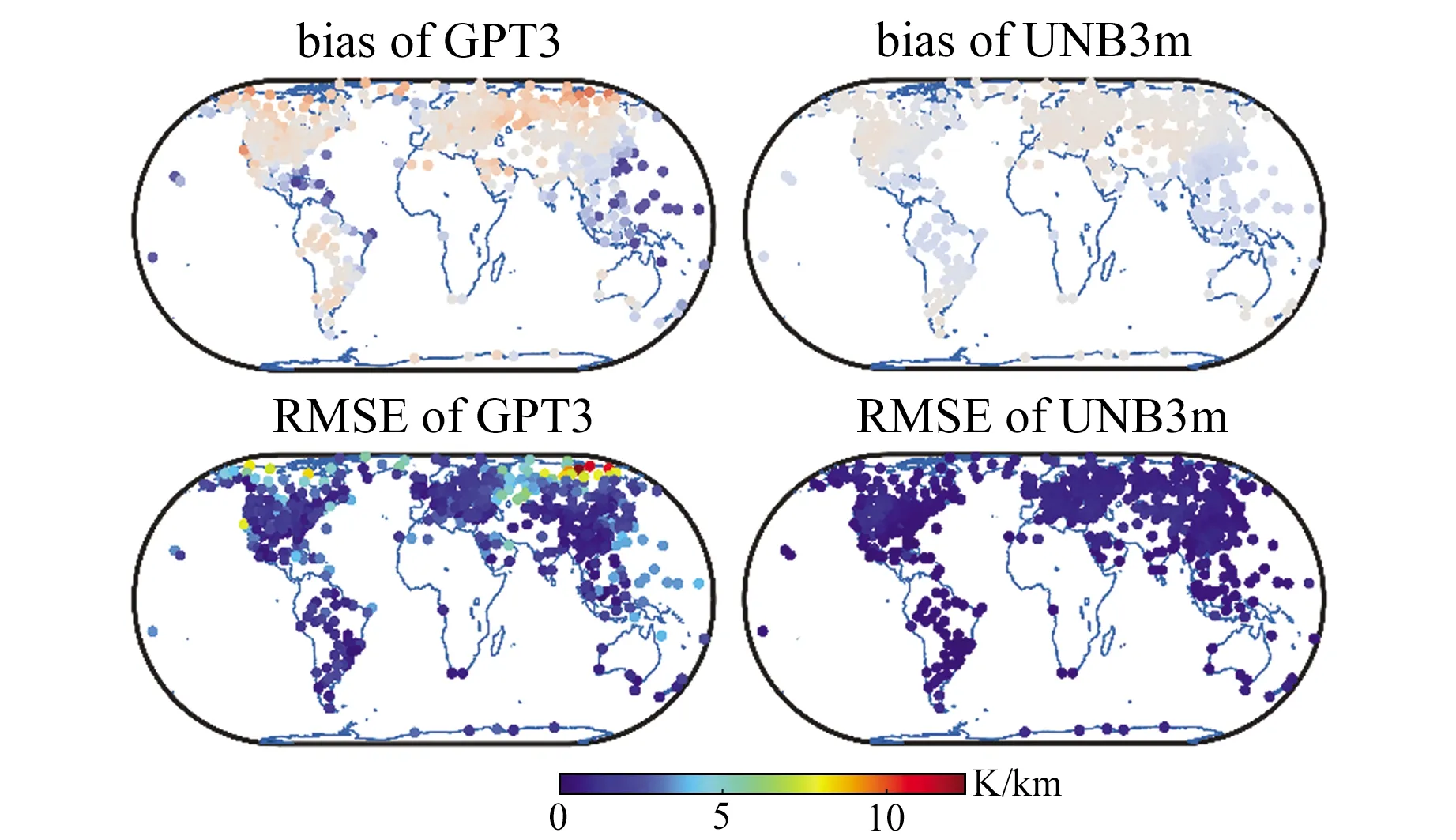
图1 全球探空站点上GPT3和UNB3m温度递减率的bias和RMSEFig.1 The global distributions of temperature lapse ratebias and RMSE as obtained by comparing GPT3 and UNB3m

表1 GPT3和UNB3m模型温度递减率的平均bias和RMSE

由表1可知,GPT3模型的bias与RMSE分别为0.8 K/km和2.3 K/km,明显大于UNB3m模型的0.2 K/km和0.9 K/km。从图1可以看出,GPT3模型的温度递减率存在明显的海陆差异,陆地区域被高估、沿海地区被低估,这可能是因为GPT3模型仅考虑了地表层的温度递减率,忽视了影响较大的下垫面条件。而UNB3m模型的温度递减率是由美国标准大气(1966年)的温度剖面数据拟合而来,反映了整体对流层温度的变化情况,与真实大气温度分布具有较好的一致性,因此其海陆差异相对较少,且精度分布更加均匀。

气压廓线估计方面,GPT3模型采用的是虚温模型,该模型本质上是等温模型,即假设大气恒温不变,因此该模型适用于存在逆温现象的地表层大气,对于温度会随高度增加而减小的整体对流层并不适用。文献[7]通过实验对比证明了GPT3模型在预测气压值时存在精度随高度增加而变差的现象,并指出随着高度差的增加,绝热模型比虚温模型具有更好的气压改正效果,为GPT3模型的气压垂直修正方法改进提供了依据。水汽压廓线估计方面,GPT3模型主要受气压与水汽直减因子的影响,气压方面可通过对气压垂直修正方法的改进提高精度;由于水汽直减因子是在数值积分得到的湿延迟基础上利用式(5)反演得到[5],具有较高的精度,无需修正。

为克服GPT3模型温度递减率只适用于地表的问题,本文提出改进模型GPT3v。选择UNB3m模型的温度递减率代替原有模型的温度递减率,其温度递减率的年平均值和年变化振幅值见表2(单位K/km),具体计算方法见文献[3]。气压垂直方向改正采用绝热模型代替GPT3的虚温模型,该模型计算公式如下:

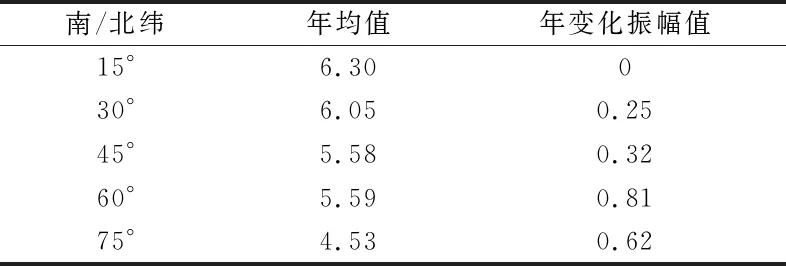
表2 UNB3m模型温度递减率的年均值和振幅值

(6)

2 GPT3v模型精度评价

为验证GPT3v模型的综合性能,利用探空数据、NCEP再分析资料和IGS ZTD数据分别对模型估计的大气参数剖面、不同高度的对流层延迟以及在实际GNSS应用场景中的结果展开精度评价。其中探空数据来自怀俄明大学,NCEP再分析资料采用美国国家环境预报中心提供的FNL数据,IGS ZTD数据来自国际全球导航卫星系统服务。

2.1 模型估计大气剖面的精度评价

本文选取2021年516个全球探空站数据作为参考值,主要包括气压、温度、比湿等气象参数。考虑到改进模型主要对温度T、气压P和水汽压e三个气象参数产生影响,因此选择这3个气象参数的大气剖面进行精度评价。首先每隔1 km将垂直剖面从地表到10 km处分为11个层;然后在同一站点、相同时间内,基于与对应层相邻高度的探空数据,利用线性插值的方式得到该高度层的温度和比湿,气压采用式(6)计算得到;最后逐层与模型估计值进行对比,误差统计结果见图2。

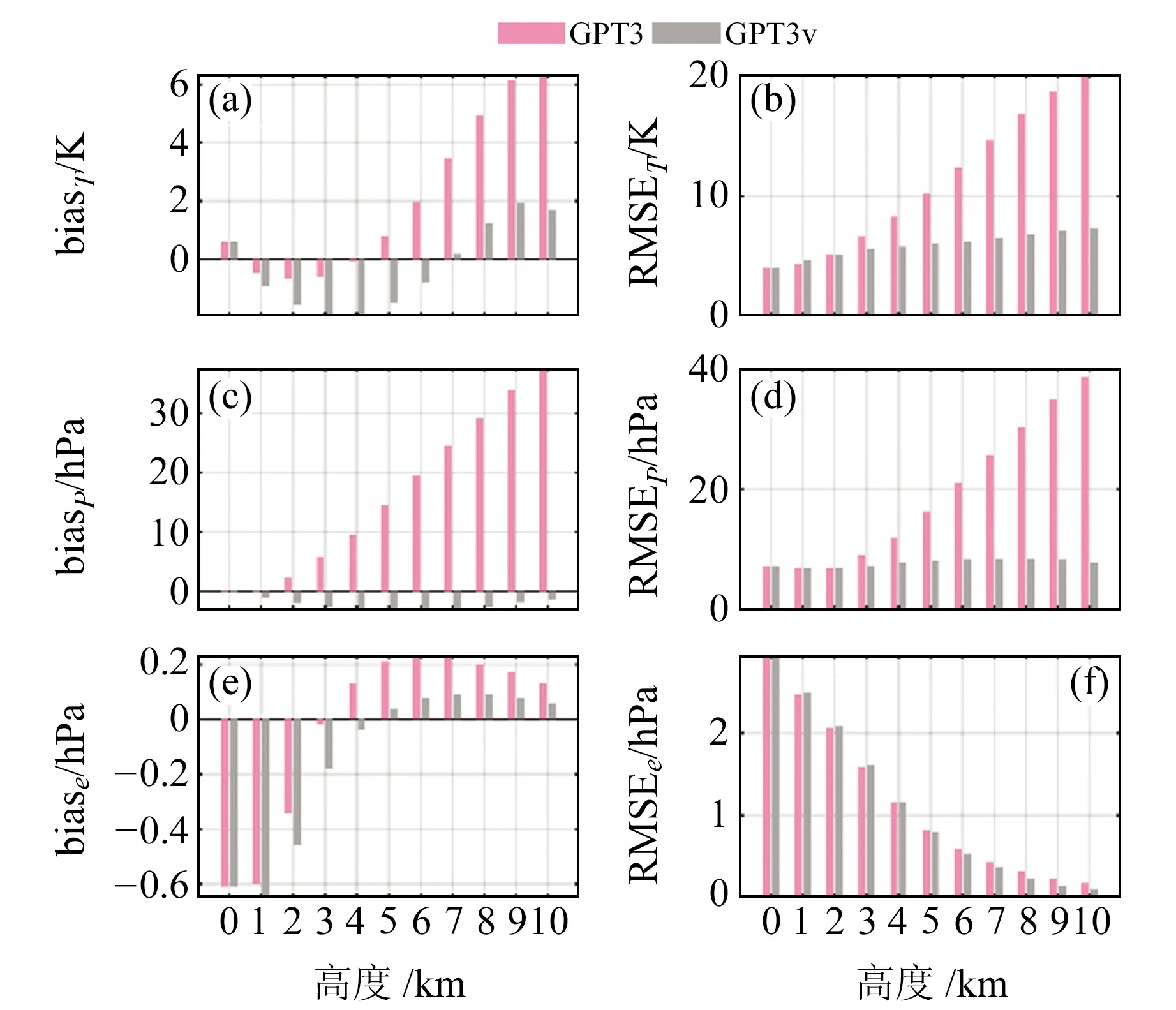
图2 GPT3与GPT3v模型在不同层气压、温度以及水气压的bias和RMSE值Fig.2 Bias and RMSE of T、P and e at different height levels for GPT3 and GPT3v models

由图2(a)可见,GPT3和GPT3v模型的温度bias在垂直方向上具有相似的变化趋势,整体呈低层大气负偏、中高层正偏。GPT3模型的RMSE在1 km处略小于GPT3v,但随着高度的增加,GPT3模型的RMSE明显增大,在10 km处达到20.2 K,而GPT3v模型仅为7.4 K,精度提高近63%。说明GPT3模型的温度递减率仅适用于近地表,而GPT3v模型则更适用于整体对流层。由图2(c)、(d)可见,GPT3模型气压剖面的bias随高度增加而增大,由0 km处的0.3 hPa增至11 km处的37.8 hPa,说明GPT3模型所采用的虚温气压改正模型导致气压被高估,高层大气中高估尤其严重。同时,这也直接导致GPT3模型的RMSE由0 km处的7.2 hPa增至顶层的38.5 hPa,这与文献[8]的研究结果一致。而改进后的GPT3v模型在所有高度层的bias和RMSE都相对稳定且较小,分别保持在-3 hPa和8 hPa左右。由图2(e)、(f)可见,2个模型的水汽压bias与RMSE在不同高度层的分布趋势较为一致,在地表处呈现明显的负偏差,说明GPT3模型在地表处的水汽压值被低估。低层大气中2个模型的RMSE较为接近,但4 km以上高度GPT3模型的RMSE略大于GPT3v。由此说明,虽然GPT3v模型对于水汽压剖面的改进程度差于温度和气压的改进程度,但也具有一定的效果。考虑整体大气剖面的估计效果,GPT3v模型估计温度、气压的平均RMSE值分别为6.0 K、7.9 hPa,相比GPT3模型的11.1 K、19.0 hPa,GPT3v模型精度明显提高。

2.2 模型估计对流层延迟的精度评价

为评价模型估计对流层延迟剖面的适用性,本文选用2021年NCEP再分析资料作为参考数据。NCEP再分析资料的时间分辨率为6 h,水平分辨率为1°×1°,垂直分辨率为31层。同样将垂直剖面分为11层,每层NCEP对流层延迟值采用Wilgan等[10]提出的积分方法进行计算,最后获得每层的ZHDL、ZWDL、ZTDL(下标L表示以该层高度为起始计算面的对流层延迟值),并与模型的估计值进行比较,误差统计结果见图3。

图3 GPT3和GPT3v在不同高度层估计ZHDL、ZWDL、ZTDL的bias与RMSEFig.3 Bias and RMSE of ZHDL、ZWDL and ZTDL at different height levels for GPT3 and GPT3v models

由式(4)可知,ZHD估计是否准确主要取决于气压的精度,因此GPT3和GPT3v的biasZHD和RMSEZHD在各层的分布趋势(图3(a)、(b))与各自biasP和RMSEP的分布趋势(图2(c)、(d))基本一致。GPT3模型的biasZHD随海拔高度的增加而明显增大,从地表的2.8 mm增至10 km处的80.3 mm,这种系统性偏差也直接导致其RMSEZHD从地表的19.6 mm增至10 km处的81.3 mm。由于GPT3采用虚温气压改正模型,因此其气压剖面估计不准确,使得ZHD估计误差较大。而GPT3v采用绝热模型的气压改正方法,其biasZHD在不同高度层保持在-6.3 mm左右。同样,GPT3v模型的RMSEZHD也较小且保持平稳,在10 km处仅为17.3 mm,相比于GPT3模型精度提高约79%。2个模型的biasZWD和RMSEZWD分布趋势几乎保持一致且数值较为接近,说明垂直修正对于ZWD剖面估计的改进效果并不明显;模型的biasZTD和RMSEZTD在低层大气中的分布情况与ZWD较为相似,在中高层大气中的分布情况则与ZHD较为相似,说明低层大气中ZTD的估计精度主要取决于ZWD,而中高层大气中的估计精度主要取决于ZHD。得益于温度递减率和气压垂直改正模型的改进,GPT3v模型的RMSEZTD随高度的增加而逐渐减小,在10 km处仅为17.1 mm,相比于GPT3的82.4 mm,精度提高近79%。考虑整体大气对流层延迟的估计效果,GPT3v模型估计ZHD、ZWD和ZTD的平均精度分别为17.9 mm、10.3 mm和23.0 mm,GPT3模型则为42.1 mm、10.7 mm和47.8 mm,这说明在估计ZHD和ZTD方面,GPT3v模型具有明显优势。

2.3 GPT3v模型在GNSS应用中的评价

为进一步分析GPT3v模型在实际应用场景中的改进效果,选择2021年384个全球分布的IGS观测站ZTD作为参考值,对2个模型的精度进行评价。由于IGS站仅提供ZTD,因此首先需要用2021年的NCEP再分析资料计算各IGS站上的ZHD,再从ZTD中分离出ZWD得到IGSZWD与IGSZHD。

GPT3、GPT3v模型的bias和RMSE结果如表3(单位mm)所示。由表可见,GPT3v模型在ZHD预测中优于GPT3,biasZHD由3.8 mm减小至3.3 mm,RMSEZHD由15.6 mm减小至15.3 mm。GPT3和GPT3v模型在ZWD计算中的bias有明显负偏,bias均为-5.8 mm、RMSE均为35.7 mm,进一步证明GPT3模型在地表处存在低估现象。

表3 384个IGS站点上GPT3和GPT3v估计对流层延迟的bias和RMSE

图4为2个模型预测ZHD和ZWD精度的全球分布情况,由图可见,ZHD的RMSE大致呈中低纬度地区小、高纬度地区大的趋势;而ZWD的RMSE则呈中低纬地区大、高纬度地区小的趋势。

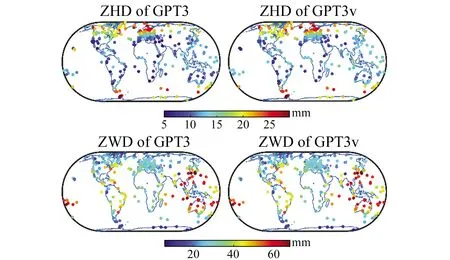
图4 GPT3和GPT3v在IGS站点上估计ZHD和ZWD的RMSEFig.4 RMSE of ZHD and ZWD at IGS stations for GPT3 and GPT3v models

考虑到GPT3模型计算的IGS站对流层延迟是由离该站点最近的周围4个模型网格点插值得到,为了进一步分析垂直改正对模型精度的影响,首先计算每个IGS站周围4个网格点高度与该站点高度的平均高度差,然后将GPT3v和GPT3模型估计ZHD和ZWD的bias和RMSE分别作差。图5为2个模型RMSE和bias的差值随高度差的变化情况。由图可见,ZHD的bias与RMSE残差多为负值,且二者的绝对值均随高度差的增加而增加,表明GPT3v模型在海拔差异较大地区的ZHD预测精度要优于GPT3模型。GPT3v模型中ZWD的RMSE在整体上与GPT3模型非常接近,该结论与§2.2中ZWD的结果一致。总体而言,相较于GPT3模型,GPT3v模型在地形复杂区域具有更好的适用性。

3 结 语

1)GPT3和GPT3v模型估计温度、气压、水汽压剖面的平均精度分别为6.0 K、7.9 hPa、1.1 hPa和11.1 K、19.0 hPa和1.2 hPa,精度提高接近46%、58%和8%,说明GPT3v模型在估计温度和气压剖面方面明显优于GPT3模型。

2)GPT3v模型估计ZHD、ZWD和ZTD的平均精度分别为17.9 mm、10.3 mm和23.0 mm,GPT3模型的平均精度分别为42.1 mm、10.7 mm和47.8 mm。二者的ZWD估计精度较为接近,但GPT3v模型的ZHD和ZTD估计精度明显提高,精度提升分别约58%和52%。因此在GNSS实际应用场景中,GPT3v模型在地形复杂地区具有更好的适用性。