高速路匝道汇入路段驾驶风格

叶 明,甘 静,胡海玉,隋 毅,杨金才

(1.重庆理工大学 车辆工程学院, 重庆 400054;2.重庆科技学院 机械与动力工程学院, 重庆 401331;3.长城汽车股份有限公司, 河北 保定 071000)

0 引言

近年来,高速公路入口匝道区域受到学者的广泛关注。已有研究表明,入口匝道是影响高速路交通流量与通行能力的瓶颈区域[1-4]。入口匝道存在的频繁汇入行为,会对主车道车流产生影响,甚至降低道路通行能力[5-6]。因此有必要对匝道汇入路段车辆的驾驶行为进行研究。

现有研究多从微观特性入手,构建数学模型对匝道交通流进行仿真分析。温惠英等[7]通过实车采集入口匝道汇入数据,考虑车流微观运行特性建立冲突概率模型,仿真结果表明该模型可以准确识别匝道合流区车辆的潜在冲突。苗旭等[8]综合考虑内部和外部因素建立回归模型实现对入口匝道的仿真模拟,该模型可实现对交通流的准确模拟,误差在12%以下。对道路交通流的模拟需要建立在准确把握时空轨迹特性的基础上。Wan等[9]通过无人机采集高速路入口匝道处的车辆轨迹,观测到高速路入口匝道路段的3种交通流状态,研究表明当间距为15～20 m时,换道车辆的切入会导致目标车道上的车辆采取强制减速。Zhu等[10]基于深度强化学习分析了不同流速下入口匝道、合流区和出口匝道的交通流特性。龙科军等[11]通过实车采集匝道汇入轨迹数据,对比分析不同服务水平下车辆的时空特性,结果表明服务水平会显著影响车辆的汇入行为。现有匝道汇入特性的研究中,多是以车辆在交通系统中的角色为中心进行展开,驾驶人作为人—车—路闭环中最不稳定的主体因素,具有个性化差异,却很少被纳入研究范围。驾驶人在行驶过程中表现出的对于油门、方向盘、跟车间距等的个性化差异即为驾驶风格[12]。由于驾驶人的驾驶风格差异,对驾驶辅助系统的预警需求也有一定区别,若不考虑驾驶风格则会出现系统与驾驶人意见相左的时刻,降低驾驶人对辅助系统的接受度[13]。如何让车辆更贴合驾驶人的行为,设计符合驾驶人期望的ADAS令其做出更安全的驾驶决策是亟待解决的问题。

综上,基于NGSIM数据集提取匝道汇入主车道路段的车辆行驶轨迹,使用无监督学习算法实现驾驶风格分类,分析汇入位置与驾驶人驾驶风格的关联,并进一步分析不同驾驶风格在匝道汇入路段的驾驶特性分布和差异。

1 数据预处理

1.1 数据来源

本文中采用的US101数据集选自美国联邦公路局(FHWA)发起的Next Generation Simulation (NGSIM)项目。NGSIM项目的研究人员于2005年6月15日在加利福尼亚州洛杉矶收集了美国101号公路的详细车辆轨迹数据。研究区域长约640 m(2 100 英尺),包含8条车道,其中1～5为主车道(车道编号从左往右依次增大),7车道为上匝道,8车道为下匝道,6车道为辅助车道,包含了单行道、匝道汇入、匝道汇出等交通研究热点区域。将其简化后如图1所示。

图1 US101车道示意图

NGSIM数据集在各种交通领域和车辆行为研究中得到了广泛应用,同时各研究也指出数据集中存在部分测量误差导致交通参量序列值噪声较大[14-15]。若忽视这部分数据集本身的误差,会导致试验结果出现误差累积。因此,在对轨迹数据做进一步的分析处理前,需要先对其进行数据清洗,以去除噪声和异常值。

对于数据中存在的随机干扰,平滑处理是最常见的手段[16]。使用SG滤波(savitzky-golay filter)进行平滑处理。采用Windows为21的SG滤波对车辆轨迹中的速度和加速度进行滤波处理,以US101数据集中ID为1250的车辆为例,去噪效果如图2所示。

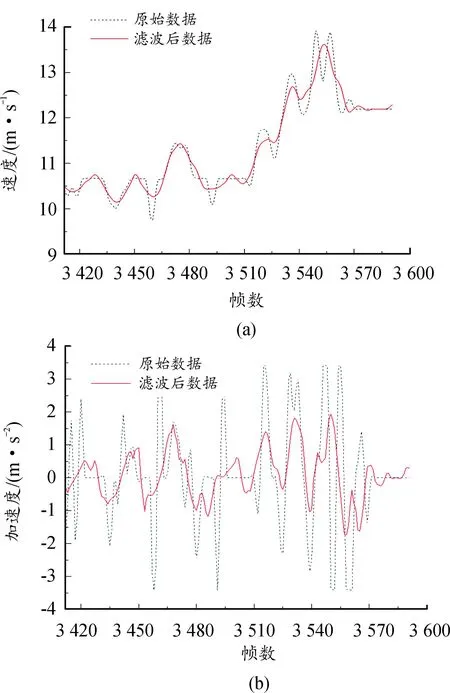
图2 SavitzKy-Golay滤波前后对比

对比图2中的原始数据与滤波后数据可以看出,原始数据中加速度的波动幅度非常大,SG滤波能够在几乎完整保留原数据的同时,缩小加速度的误差。通过计算速度和加速度方差和均值发现,加速度的方差数值由2.42下降到了0.55,其余值均在0.001的误差范围内,足见SG滤波去除数据噪声的优异能力。

1.2 数据筛选

由图1可知,US101道路的上匝道入口在200 m左右的位置,车辆并不会在匝道口直接汇入主道,而是会依照原来的方向继续行驶一段距离,因此将匝道汇入路段适当往车辆行进方向延伸,定义匝道汇入场景为前250 m区间。匝道汇入场景的数据样本提取逻辑为:

1) 车道约束,选取由第7车道(上匝道)汇入主车道的车辆。

2) 异常数据剔除,为保证数据的准确性,定义换道行为只能发生在相邻的车道之间。例如,它不能在一个时间步长(0.1 s)中跳过一个车道。所有出现这种不可行变道的车辆都将被剔除。同时假设在极短时间内发生超车行为的车辆未换道。

根据数据样本提取逻辑,最终得到256辆由匝道汇入主车道的完整车辆轨迹数据。在匝道汇入合流区的过程中,在辅助车道上的汇入位置是一项重要的研究点,以10 m为单位进行统计,得到汇入位置的分布直方图如图3所示。从图3可知,车辆主要集中在辅助车道的10～60 m处汇入合流区,占比为53.51%;41.01%的车辆在60 m后汇入;5.48%的车辆在10 m前汇入。

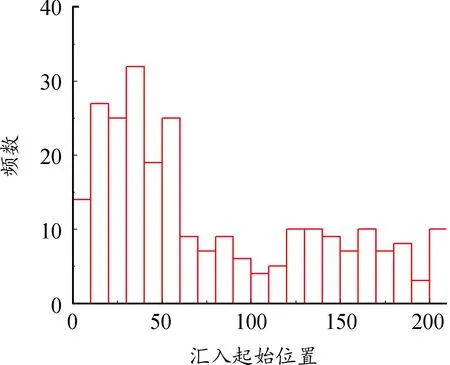
图3 汇入起始位置分布直方图

2 降维

由于初步选取计算得到的特征参数统计值类别多,参数之间容易存在信息重叠,进而导致后续分析时结果不理想,计算量增大,因此需要对数据进行降维处理。在最大化保留原始变量信息的同时,将原始复杂且多维的变量通过线性组合转换为低维度的新变量,这类分析过程被称为数据降维。主成分分析(principal component analysis,PCA)和因子分析(factor analysis,FA)是数据降维的主要手段[17]。

因子分析法是对主成分分析法的延伸,2种方法都是通过相关系数或协方差矩阵的特征值与特征向量之间的不相关的特性,将原始变量综合成不相关的新指标[18]。在考虑变量间内部关系时,因子分析更加贴近实际情况,其次由于因子载荷矩阵的可旋转性,能够更好地对公共因子进行解释,这有助于后续对驾驶风格的进一步研究及分析。为了更好地解释变量含义,提取出重要度较高的变量,选用因子分析对初步选取的原始多维特征参数进行降维处理。

2.1 驾驶风格特征参数选取

换道是分析驾驶行为和驾驶风格中最重要的因素之一,根据车辆换道意图,可分为强制换道和自由换道[19]。当前方有障碍或行驶路线要求必须换道时做出的换道行为则为强制换道。考虑到在匝道汇入路段中,会同时存在这2种换道类型,故对其进行定义和区分:定义强制换道为从上匝道汇入主道和从下匝道驶离主道的变道行为,具体类型如图4所示。

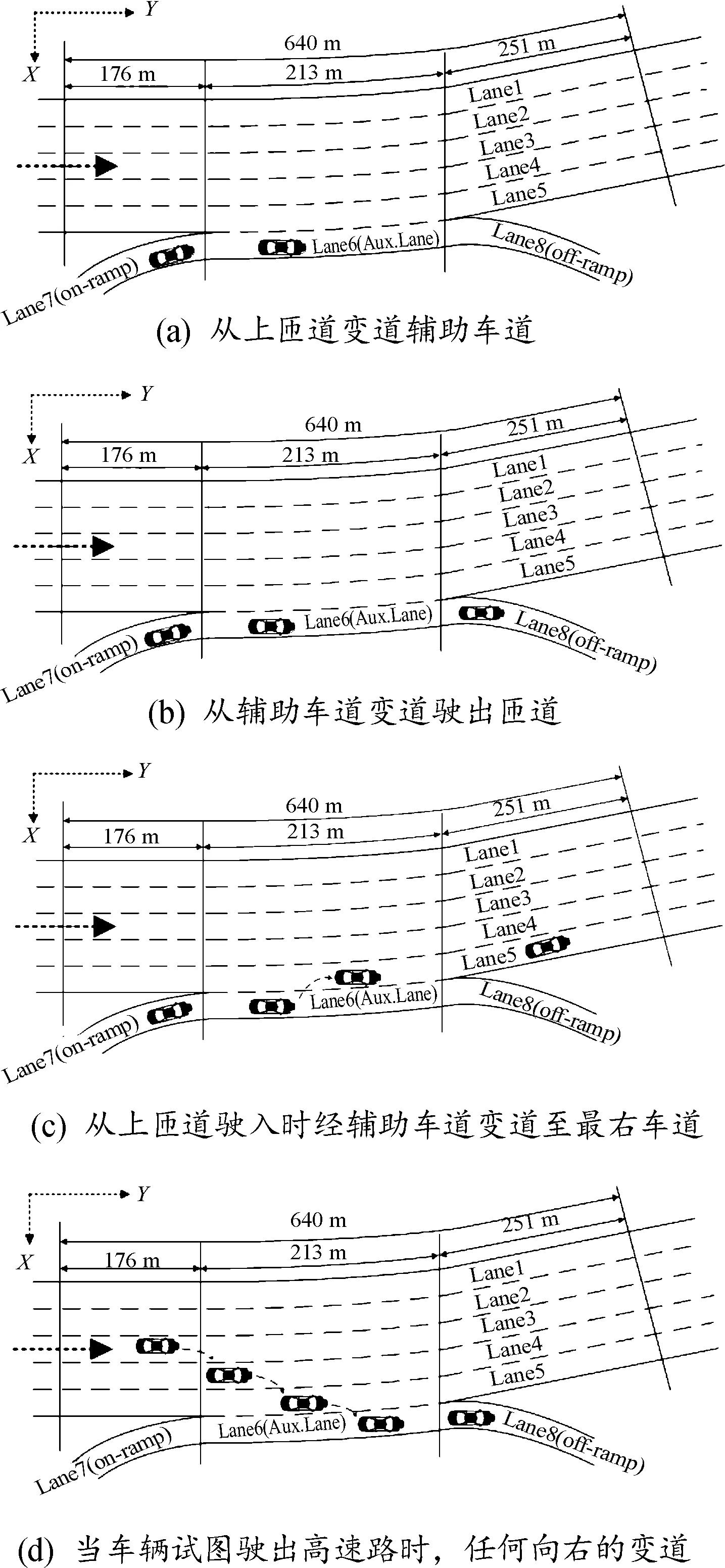
图4 4种强制换道具体类型

除上述4种变道类型之外的为自由换道。同时考虑到在匝道汇入路段车辆存在连续换道行为,引入自由换道次数作为驾驶风格特征参数。根据前文的分析,部分车辆在入口匝道路段未汇入合流区,因此引入在辅助车道(即第6车道)上的行驶距离作为驾驶风格特征参数。引入车头间距均值及其方差用来分析入口匝道的运行效率[20]。本文中选取的全部驾驶风格特征参数如表1所示。

表1 特征参数

2.2 因子分析

对所选取的特征参数进行降维处理,图5所示为主成分贡献率情况。

图5 主成分贡献度

前5个因子特征根值均大于1,且累积方差解释率为82.32%,能够将原始指标大部分的信息量很好地表达,将其作为反映原始指标的信息量可以认为是有效的,即原来的13个驾驶风格特征参数指标可以综合成5个公共因子,可代表原始多维特征参数,故提取因子个数为5。

使用Kaiser标准化正交旋转法将因子载荷阵旋转得到旋转成分矩阵,如表2所示。

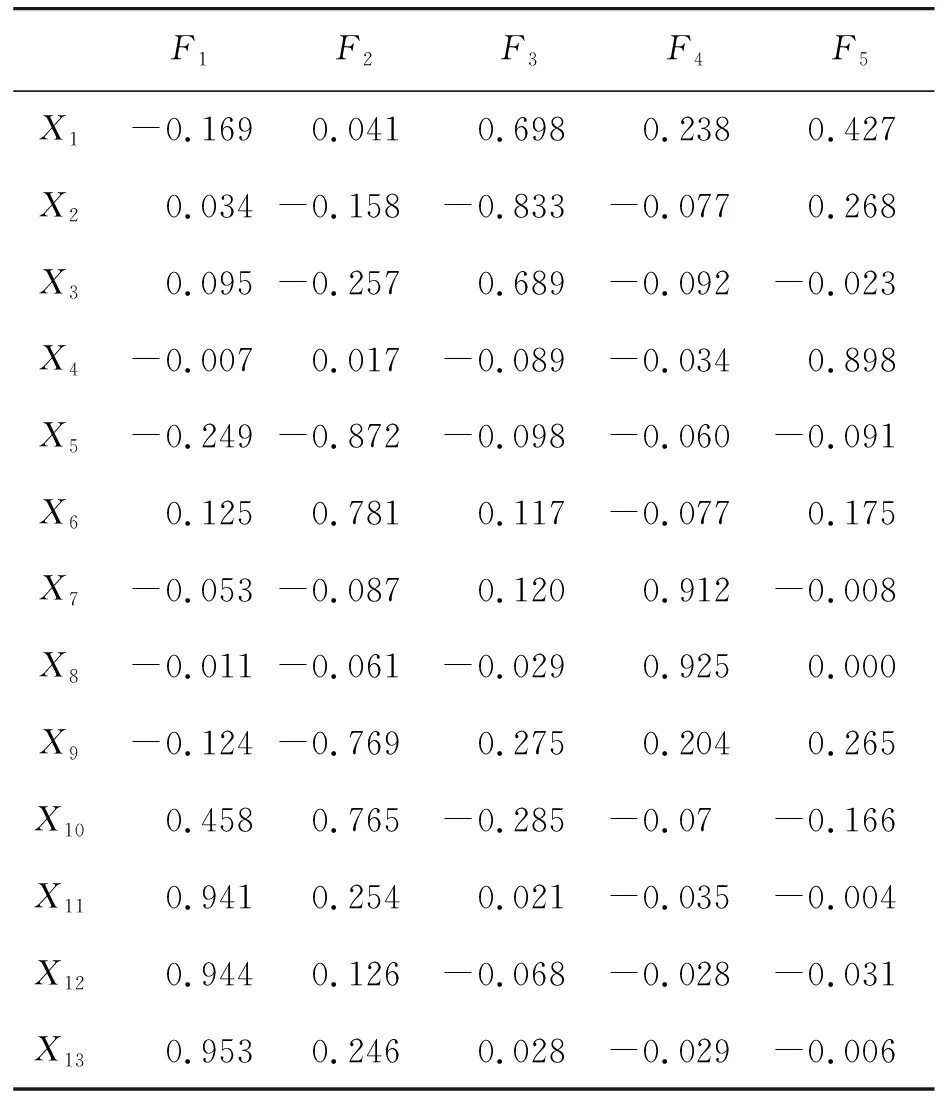
表2 旋转成分矩阵

通过表2可知,第一因子变量F1中自由换道次数、换道时间有较大的载荷,因此将其命名为换道因子;第二因子变量F2中横向速度平均值、横向速度方差及总车道数有较大载荷,因此将其命名为横向因子;第三因子变量F3中纵向速度均值、纵向速度方差及加速度均值有较大载荷,因此将其命名为加速度因子;第四因子变量F4在车头间距平均值及其方差上载荷较大,因此将其命名为跟驰因子;第五因子变量F5在加速度方差上载荷系数较大,而加速度方差可表现车辆速度波动,因此将其命名为速度波动因子。

于是可得到前5个因子的得分系数如表3所示,根据因子得分系数矩阵建立综合特征参数样本矩阵。

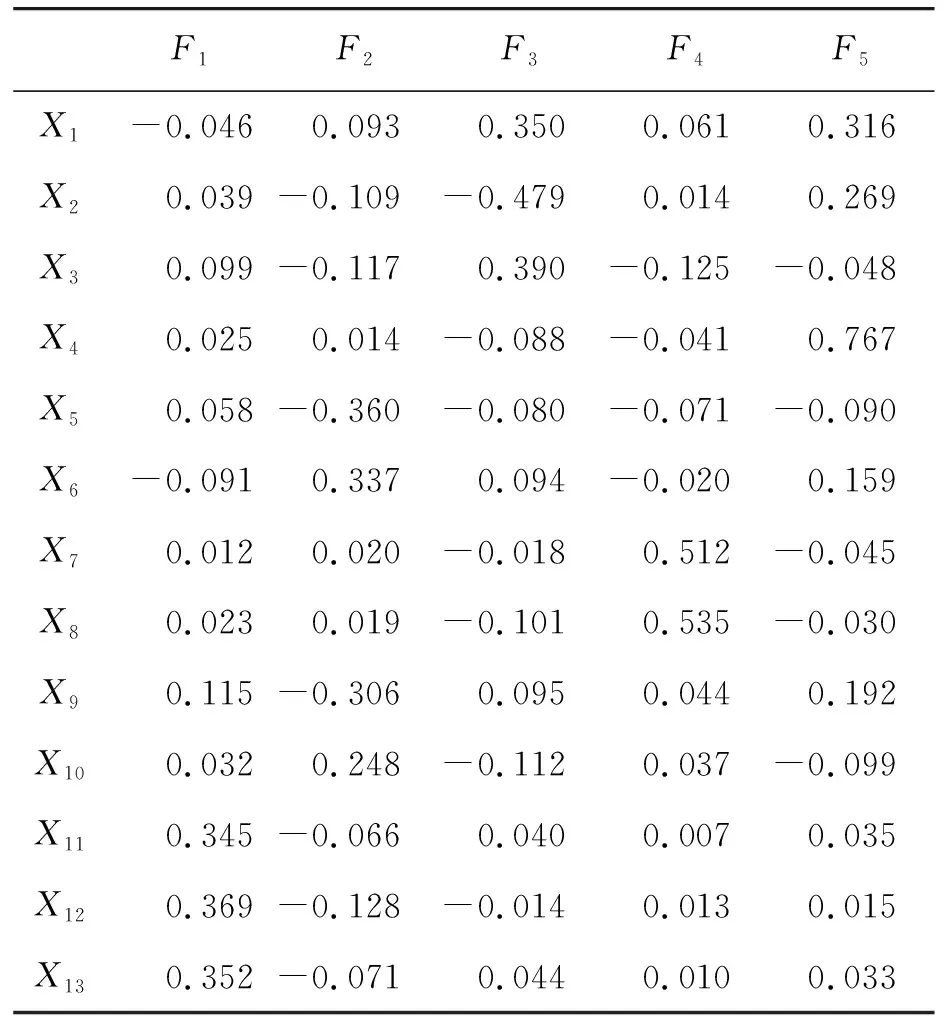
表3 因子得分系数矩阵

可由表3得到5个因子的表达式:

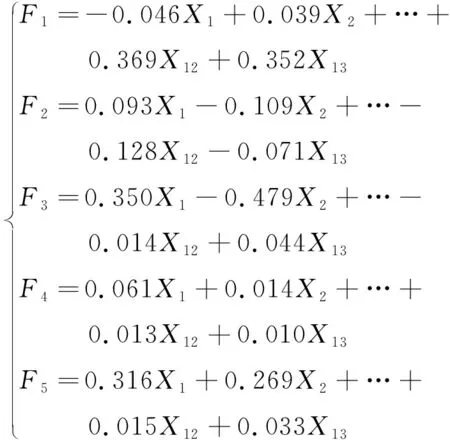
3 聚类

本文中考虑2种聚类算法:K-means算法和谱聚类。在K-means算法中,选取K-means++优化初始聚类中心。

3.1 聚类算法

3.1.1K-means算法

K-means是一种以距离作为分类准则的算法,通过迭代更新聚类簇的平均值,重新分配聚类中心,直至聚类中心不再改变或者收敛,则聚类过程结束,返回当前聚类结果[21]。但是由于K-mean聚类算法的初始聚类中心为随机选取,聚类时需要迭代多次以弱化伴随随机初始化不稳定性,这会直接影响到最终的聚类结果。为了避免这一问题,K-means++算法应运而生。

K-means++算法的核心思想是选取距离尽可能远的数据点作为初始聚类中心点,这样可以有效解决聚类结果对初始聚类中心选取过于依赖的问题。

设D={x1,x2,…,xm}为原始数据集,现将数据集划分为C={c1,c2,…,ck},K-means++算法中初始化聚类中心点的具体计算步骤如下:

1) 从数据集中随机选择k个样本点作为初始聚类中心ci。

2) 计算每个样本点与初始聚类中心ci之间的最短欧氏距离D(x);接着计算每个样本点被选为下一个聚类中心的概率;最后,使用轮盘法作为选取法则选出下一个聚类中心。

3) 重复,直至选出k个聚类中心为止。

3.1.2 谱聚类算法

谱聚类方法起源于谱图理论,其原理是通过对样本数据的拉普拉斯矩阵特征分解进行聚类来得到新的图的划分,对应聚类算法的聚类过程。对于谱聚类而言,图划分的最优准则选取将会直接影响聚类结果[22]。

谱聚类可分为3个步骤:依次是相似图矩阵构建、图切割和聚类分析。假设给定样本数据集X=[x1,x2,…,xd]=[x1,x2,…,xn],即数据集含n个样本,每个样本有d维特征。算法具体流程如下:

1) 根据样本输入X构建相似图矩阵S,对数据集特征进行抽象表达;

2) 根据相似图矩阵构建拉普拉斯矩阵L;

3) 对L特征分解,对特征值进行排序将特征值按从小到大的顺序排列,计算并选取前k个特征值所对应的特征向量,组成谱表示矩阵F;

4) 使用聚类算法(如K-means,模糊聚类等)对F中的特征向量进行聚类,将新的样本点Y={y1,y2,…,yn}聚类为C={c1,c2,…,ck},得到k个聚类簇数。

3.2 评估指标

为评估聚类算法的分类效果,使用轮廓系数对聚类结果进行评价。轮廓系数(silhouette coefficient)[23]是通过将同一簇内物体的平均距离与其他簇中物体的平均距离进行对比得到的,可衡量内聚度和分离度的优劣。聚类内相似度高、聚类之间相似度低的聚类将具有较高的SC值。假设聚类后的结果为k个类簇,C={c1,c2,…,ck},对其中一个点Xi,其轮廓系数S(i)表示为:

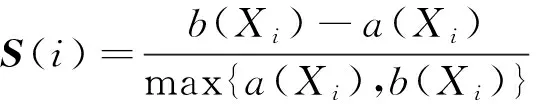
(1)

式中:a(Xi)是点Xi与同一类簇中ci所有点之间的平均距离;b(Xi)是点Xi到其他簇中各点的最小平均距离。

对于一个样本集合,它的轮廓系数是所有样本轮廓系数的平均值,可由式(2)得到:

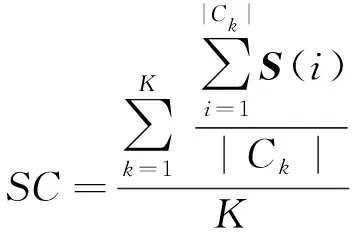
(2)

轮廓系数取值范围在[-1,1],若趋近于1,则说明同类样本间距离越近,不同类别间样本距离越远,说明聚类结果越好。

3.3 聚类结果

为更好地对驾驶风格进行语义解释及区分,现有研究大多倾向于将驾驶风格分为2～4个。本文中定义聚类簇数为3,将K-means++算法的聚类结果与其他算法进行比较,引入轮廓系数对其进行评估,如表4所示。通过对比轮廓系数可以发现,在列举的3类算法中,K-means++取得最优的结果,故本文中使用K-means++聚类结果作为驾驶风格分类的依据进行后续研究。同时以K-means++为聚类模型,对比降维前后的轮廓系数,见表5所示,可以发现使用因子分析降维后的特征序列可以得到更好的分类结果,这说明降维可以有效提取原始特征中的信息。

表4 不同聚类模型对比

表5 降维前后聚类效果对比

使用K-means++聚类得到的各驾驶风格聚类中心列表如表6所示,可以发现在所有类别中,类别3的换道因子F1、横向因子F2的中心值最大,这说明该类型有更多的自由换道行为,同时跟驰因子F4最小,这说明该类型存在强跟驰现象,车辆与前车的间距小;类别1中的加速度因子F3最大,反映出该类型驾驶人在匝道汇入过程中的速度保持在较高值;速度波动因子F5在类别3中最小,类别1中最大,这反映了类别1的驾驶人具有更频繁的加减速行为。综合以上分析,对驾驶风格进行命名,命名类别1为谨慎型,类别2为稳健型,类别3为激进型。可以发现,激进型的驾驶风格更倾向于多次换道,并且在整个匝道汇入的过程中与前车的间距更近。

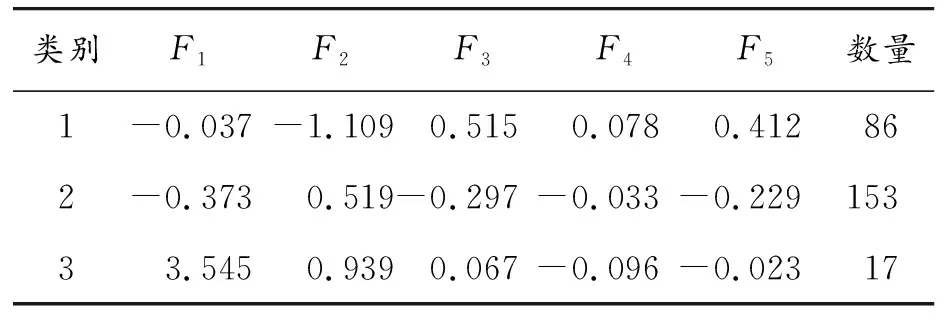
表6 聚类中心

在1.2节对匝道汇入起始位置分布做了分析,但并未对驾驶风格进行区分,为进一步观察不同驾驶风格汇入合流区的位置选择差异,将车辆切入合流区时刻的位置与其在上匝道的终止位置作差,可视化得到图6。需要注意的是,图6中的位置分布限定在入口匝道路段,实际上是在辅助车道上的行驶距离,由于在本路段多数车辆已完成了从匝道汇入合流区这一驾驶行为,因此本小节仍以匝道汇入起始位置切入进行分析。以5 m为单位进行统计,并进行曲线拟合,发现其位置分布均符合正态分布,激进型峰值在20 m左右出现,稳健型则在30～40 m内出现,谨慎型选择汇入合流区的位置最远,峰值出现在100 m左右的位置。

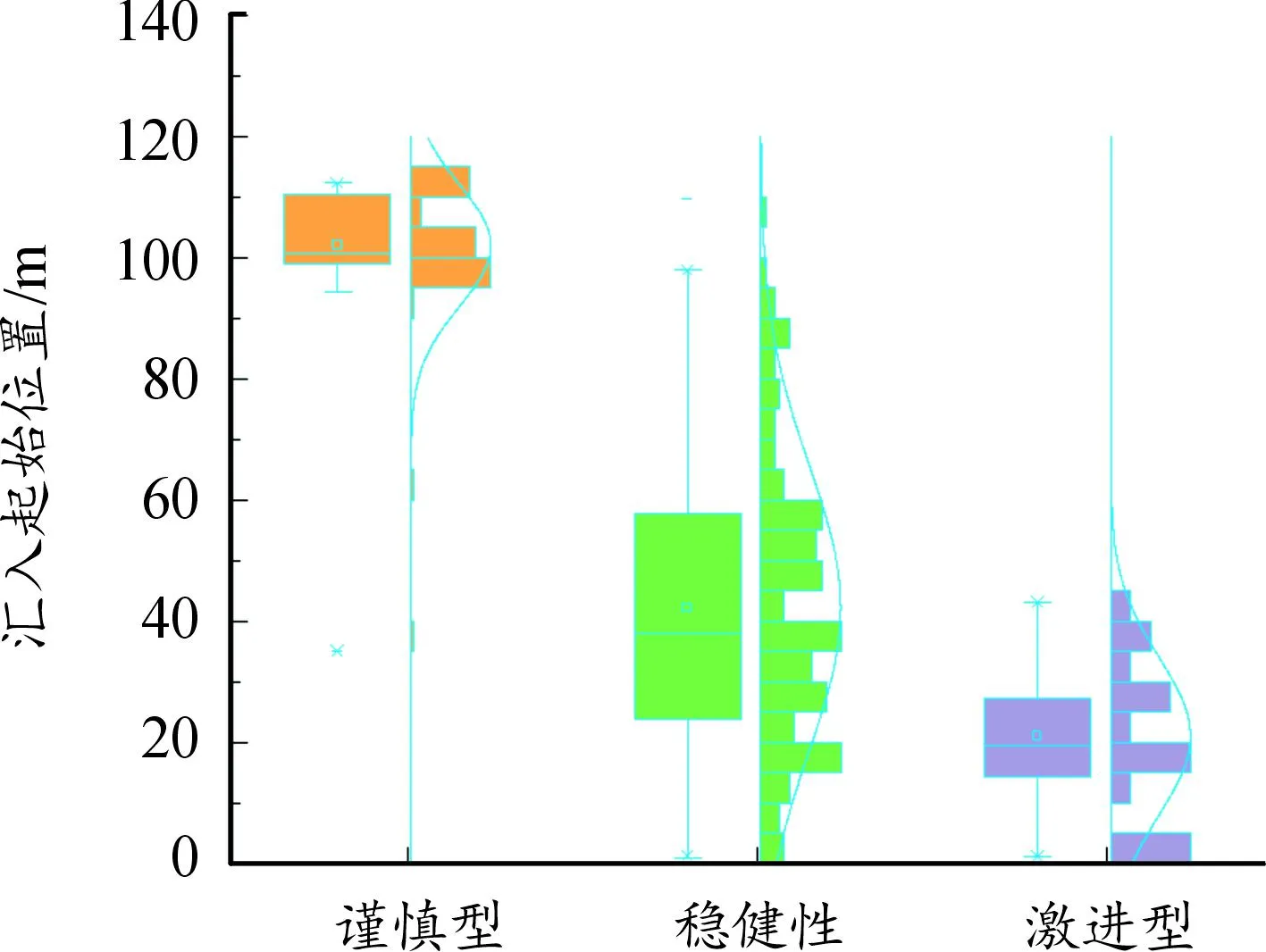
图6 不同驾驶风格汇入合流区的位置分布

为找出谨慎型与另外2种驾驶风格在汇入合流区位置分布差异的原因,将5个主因子对应的驾驶风格特征参数进行分析,列出3种驾驶风格各特征的均值,见表7所示,将部分参数可视化如图7所示。

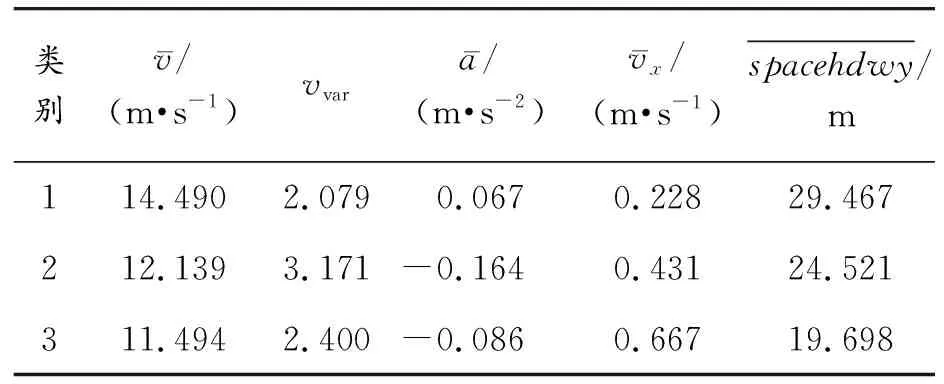
表7 不同驾驶风格特征均值

图7 不同驾驶风格特征参数分布

通过速度的均值分布可以看出,3种驾驶风格中谨慎型的速度最大,而其速度方差最小,为2.079,对比其加速度分布可知,在汇入合流区的过程中,谨慎型驾驶人的加速频次高于减速频次,倾向于使用更多的时间和更长的行程来寻找切入合流区的时机。因此,该类型驾驶人相较激进型与稳健型在入口匝道路段的横向速度整体较小,并且由于未参与该路段的合流区汇入行为,其车头间距维持在较大值。

而分析激进型驾驶风格的各项特征可以发现,激进型驾驶风格的平均速度最小,为11.494 m/s,虽然与稳健型的差距不大,但观察其分布可以发现稳健型的分布更集中更均匀;同时由于2种风格都倾向于在短程内汇入合流区,其减速频次比谨慎型更高,加速度平均值也呈负值。从车头间距分布可以发现激进型与稳健型驾驶风格都维持在20 m左右,这说明在这段区域,车辆汇入的通行率是较高的。

4 结论

1) 为分析不同驾驶风格的驾驶人汇入匝道的驾驶风格差异,选取K-means++、K-means和谱聚类分别对数据样例进行聚类,对比各自的轮廓系数发现K-means++的聚类结果最优。将降维前后的特征序列使用K-meas++进行聚类,发现因子分析可以有效提取关键信息。

2) 分析不同驾驶风格,结果表明激进型与稳健性驾驶风格均能在短行程内完成匝道汇入,而谨慎型由于对汇入时机把握得不恰当,不得不提高车速在辅助车道上行驶更长的距离。