基于外存八叉树STL 模型的拓扑重建方法

翟晨龙， 朱冬梅， 贺可太， 孟晓伟

（北京科技大学机械工程学院， 北京 100083）

0 引言

快速成型技术几年来发展迅速， 如Selective laser melting（选择性激光熔化）、Fused Deposition Modeling（熔融沉积制造）、Digital Light Processing（数字光处理）等，这些制造方式改变了原来的制造方式由减材制造转向增材制造，STereoLithography（STL）文件是增材制造领域常用模型文件， 随着增材制造技术发展需要打印的模型具有的结构也变得更复杂，STL 模型文件所需的存储空间变大。STL 模型由大量三角面片组成，储存信息时每个三角面片三个顶点坐标和法向量[1]，由于STL 文件不包含任何拓扑信息和表面结构， 模型上某一顶点将被多个三角面片共有， 共有的顶点数据被重复保存导致大量信息冗余。 STL 文件储存方式可分为二进制和ASCII 码两种方式各有优缺点， 二进制储存形式占用空间小但不可修改信息不可见读取速度快，ASCII 码形式占用空间大读取速度慢内容可修改， 这就导致打开大型模型文件时需要更多时间， 在进行大数量网格模型缩放或者移动时就会导致卡顿， 为了满足增长性能要求同时尽可能保证模型特征，需要优化模型组织和管理方法，使用多分辨率对象在网络波动时平滑地适应图形环境视觉质量， 还可以利用贪婪调度策略最小化用户收到的错误[2]实现不同分辨率下动态表示模型可以采用Levels of Detail（LOD 技术，LOD技术意为多细节层次， 它能够根据视距和视角不同采用不同分辨率显示模型，能够很好符合人机交互的要求，所以LOD 技术常被应用与大规模数据管理和调度。 在表示三维地形使用细节层次模型（LOD）、四叉树和局部曲率熵，通过三者结合可以灵活控制四叉树深度并动态调度大规模LOD 地形，利用四叉树可以消除不同LOD 之间裂纹[3]；加载大规模摄影三维模型同样可以使用分层多分辨率的思想，采用网格+四叉树+十六进制树构建空间索引，使用分层分块的3D 模型，满足海量模型可视化和实时交互的要求[4]。在制图软件中打开STL 文件时可以看到模型由三角网格构成，在曲率变化大的部分细节表达不够充分，可以使用等人提出基于视觉显著度加权的算法用于解决网格简化中尖锐特征保持差的问题， 通过平衡不同区域权重，优化局部区域特征保持问题[5]。 三角网格在拓扑结构中属于非结构化网格， 它与结构化网格区别在于非结构化网格每个结点周围的单元数目可能不相同如三角网格一个顶点至少有三个及其以上的三角单元； 虽然在信息访问不如结构化网格简单和求解程序更有效率， 但表达复杂几何体时非结构画网格存在优势， 非结构化网格因其形状具有任意性所以它具有良好的几何适应性， 网格生成算法自动化程度更高，Delaunay 三角剖分法是一种构建三角网格的算法具有拓扑性、最大化最小角和易于扩展性的优点，Guo J 等人使用约束的Delaunay 三角剖分调整参数域的边界实现了高精度和高质量的重新网格化算法[6]，双曲面Delaunay 三角剖分由最小剖分数量的问题[7]。八叉树是一种数据结构，具有访问效率高、数据插入和删除操作便利且高效和数据有序空间利用率高的优点，Koh N，Jayaraman P K 等提出一种新的八叉树结构截断八叉树，它可以自适应地修建顶部去截断树，扩展了节点随机访问和大数据集的核心外流提供了高效的查询性能[8]，Saputra A 等人利用八叉树分解分层网格将RVE 转换成数值模型，将每个八叉树单元建模为边界多面体元素，取得更好的模型均匀化效果[9]将坐标信息存储到子结点中读取不同子节点可以实现模型网格的变化，Tu T 提出将外存八叉树映射到数据库结构， 所有八叉树操作可以通过查询和更新数据库来完成[10]。 本文将STL 文件坐标存入八叉树结构， 解决上述使用非结构化网格和STL 存储特性导致文件读取速度慢的问题，实现多细节层次管理，提出基于八叉树多细节层次三维网格模型， 对STL 文件进行拓扑重建。

1 实验流程

用于智能制造领域，三维建模方向，提高STL 模型打开效率和实现多分辨率显示要求， 采用基于八叉树存储结构对STL 模型进行拓扑重建首先将三维模型投影到二维平面，在二维平面进行网格划分，并将划分好的网格映射到三维模型上，如图1 所示。

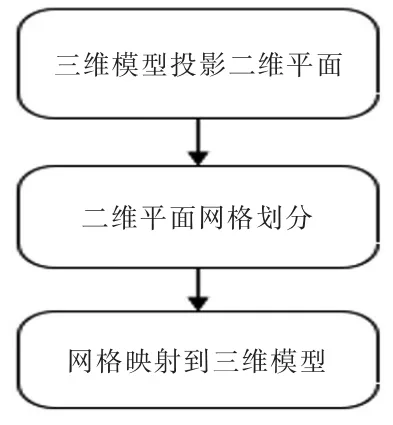
图1 整体流程图

总方法可以分为三个部分首先将模型进行分割并将分割好的子分部投影到平面上并将点集储存到八叉树树中第二部分在平面使用Delaunay 三角形法进行网格划分第三部分将划分好的网格投影到对应子部分表面。

2 STL 模型拓扑重建方法提出

2.1 三维模型分割和平面点集获取

三维模型分割可以在空间根据特征不同将模型分割， 在三维模型进行简化时采用引入图卷积神经网络的模型分割简化算法，经过训练后分割效果良好[11]，也可以将模型分成多模态二维进行表示，Pires C 提出一种级联模型模型分为两个阶段， 第一阶段检测阶段提取边界特征，然后将这些边界框送去第二分割阶段，通过这种方法提高了图像处理时间并获得了更好的分割分数[12]QinNN等人通过扫描点云提取出几个低层判别局部特征将三维地形转变为多模态二维表示， 通过并取得了理想的识别地形点云的效果[13]模型分割中存在过度归一化问题，Zhu L[14]提出一种Explored Normalized Cut（ENCut）模型分割方法一定程度上解决了过度归一化问题增强小对象分割，大型三维模型结构复杂分割算法运行时间更长，Yu L 等[15]将MobileNetv3 与DeepLabv3+ 相结合提出改进的DeepLabv3+网络轻量级语义分割算法， 提高了两者结合降低模型复杂度，提高模型运行效率。

本文采用将三维STL 模型根据法向量夹角不同将模型进行分割，再将分割子部分投影到平面获得点集，三维模型往往都是封闭的实体， 在投影到二维平面存在同一个（x，y）坐标上存在不只一个坐标，如果直接将三维模型投影到二维平面就会导致模型重叠如图2 所示这两个三角面片在Z 方向上投影的话就会发生干涉现象， 这样划分出来网格会有部分缺失的现象。

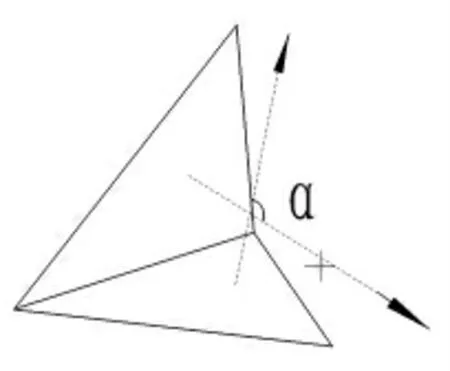
图2 某方向上三角面片重叠现象

所以需要对三维模型STL 文件进行处理， 避免产生上述问题。 采用的方法是基于法向量分割模型， 利用STL 文件储存特征进行模型的分割，STL 文件存储了每个三角面片法向量和顶点坐标，根据法向量夹角大小可以将封闭的三维模型剖分看，首先任选一个三角面片作为基准从该三角面片向外进行扩散判断其他三角面片法向量与基准法向量的夹角是否小于设定阈值， 如果小于阈值则与基准三角面片构成新的模型， 直到有三角面片法向量与基准法向量夹角大于阈值则停止该方向的判断，所有方向都判断完毕，保存第一部分分割模型。 开始下一次分割模型首先从剩余三角面片选一片作为基准， 与其他三角面片进行法向量夹角判断直到整个模型被分割成几个子区域并记录最后一个三角面片坐标值，确定该三角面片为特征三角面片，该面片某一条边位于特征边上，不同子部分由特征边分隔开，以典型零件凸轮为例，查看分割效果如图3 所示，不同子部分表使用不同颜色表示。 当对某个子部分进行投影时，使用AABB 包围盒将子分部包裹， 然后进行三维空间坐标变换， 使得基准法向量与Z 轴重合。 空间中的坐标变换可以拆分为旋转和平移， 只需要求出旋转矩阵和平移矩阵就可以让每个子部分基准法向量与世界坐标系Z 轴重合。

图3 典型零件模型分割

其中：RxRyRz为沿X 轴、Y 轴和Z 轴的旋转矩阵，X1Y1Z1为基准法向量局部坐标系三维坐标，X、Y、Z 为基准法向量世界坐标系下的坐标。

其中：α、β 和δ 分别为沿X、Y 和Z 轴方向转角。

而后进行平移操作，使得两个坐标系原点重合。

其中：T—平移矩阵；△x、△y 和△z 为X、Y 和Z 轴平移量。

由于STL 模型是由点和法向量形成的三角面片组成，所以将三维Z 坐标归零可以在二维平面上的点云，将包围盒和三维坐标（x，y，z）中Z 坐标值归零，同时将构成子部分边界的点和包围盒点以Z 坐标为零的形式存储到TZBList 表中并调用TZBList 表， 在二维平面将子分部边界点都连接可以将模型轮廓描绘出来同时也形成了包围框，实现三维模型的平面化效果如图4 所示，最外围的边框是AABB 包围盒的投影。

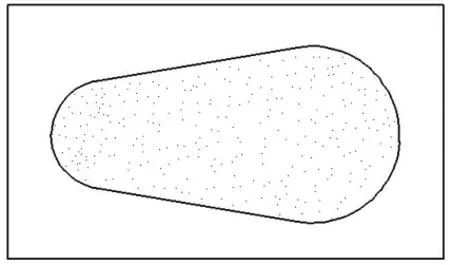
图4 三维曲面平面化

当点集投影到平面后，将点集存储到八叉树中。

2.1.1 分割和点集投影算法流程

创建Vertex 函数表示具有x，y 和z 坐标点，Triangle函数包含三个顶点实例和三角形的法向量，Mesh 结构包含所有Triangle 实例。

（1） 调用ReadSTL 函数读取STL 文件三角面片信息并将数据存储在Mesh 结构中。

（2）调用SegmentModel 函数，SegmentModel 功能是将一个三角网格模型（由一组三角形组成）根据给定的角度阈值分割成不同的部分。具体来说，函数将输入的三角形列表按照一定的方式分组， 使得每个分组内的三角形法线向量之间的夹角小于等于给定的角度阈值。这样，分组后的每个部分都可以看做是在一个平面上的一个封闭的曲面区域， 可以被单独处理或渲染。 该函数接受两个参数： 一个Triangle 类型的向量和一个double 类型的角度阈值。 函数返回一个Triangle 类型的向量的向量，每个向量都表示一个被分割出来的部分，其中包含一组三角形。

该函数的实现过程可以描述如下：

初始化一个Triangle 类型的向量列表parts。 遍历输入的三角形列表，对于每个三角形Triangle：如果parts 为空，将Triangle 添加到一个新的向量内，将该向量添加到parts 中。 否则，遍历parts 中的所有向量part，找到法线向量与Triangle 法线向量夹角最小的向量。使用使用Cosine函数计算两个Vertex 实例之间的角度的余弦值之后用IsAngleGreaterThan 函数检查两个向量之间的角度是否大于给定的阈值。 如果该向量的法线向量与tri 法线向量夹角小于等于给定的角度阈值， 将Triangle 添加到该向量中。 否则，将Triangle 添加到一个新的向量内，将该向量添加到parts 中。 返回parts。

（3）调用writeSTL 函数将分割后子分部写入STL 文件中， 它需要接受两个参数第一个是std：：string 类型的文件名，表示要写入的文件的路径和文件名。第二个参数是一个Triangle 类型的向量，包含要写入的三角形数据。

（4）将分割好的子部分进行点集投影首先调用read-STL 函数读取STL 文件中的三角形信息。 然后选择其中一个三角形的法向量作为平面的法向量， 并将平面上的一个点设置为原点。接下来，将所有三角形的顶点投影到这个平面上，并将所有的投影点保存到一个向量projectedPoints 中。最后，将所有投影点输出到一个文本文件中。

2.1.2 二维平面进行八叉树网格划分

在读取平面点集后， 通过Delaunay 三角形法进行平面网格划分，Delaunay 三角形法是将给定点集进行连线，划分三角网格的网格划分方法， 它划分三角形原理是保证组成三角网格三个顶点形成的外接圆内不能包含其他点， 这样做可以减少出现夹角狭小的三角形的可能性算法具体步骤如下：①将点集进行Delaunay 三角剖分，得到由三角形组成的网格；②进行边从属判断，判断这条边属于几个三角形（至多两个）如果只属于一个三角形。 那么将加入到最终网格中，如果属于两个三角形的公共边，则将两个三角形组合成四边形， 再将四边形拆分成两个三角形存入最终的三角网格； ③进行三角形外接圆阈值判断，当半径小于设定阈值时拆分成三个小的三角形，这么做是因为当半径过于小时意味着这个三角形的形状非常扁平，会造成数值计算的不稳定和精度问题，将狭长三角形拆分成三个小的三角形可以保证三角形外形更合理提高稳定性，拆分这个操作还会提高三角网格局部稳定性。

2.2 算法流程

（1） 调用PointReader：：readpoints 函数读取点集文件， 读取后存储在vector〈PointZ〉pointsZ 中遍历pointsZ，将每个元素x，y 坐标存储在vector〈point〉points 中， 之后遍历Points 将其每个元素的x，y 坐标输出到控制台。

（2）创建名为”Points”的窗口，并在窗口绘制points 中的每个点。

（3）进行Delaunay 三角剖分，通过调用OpenCV 库中的Subdiv2D 类和getTriangleList 函数来完成。 该函数将points 中的点作为输入，生成了一组三角形，并将其存储在vector〈Vec6f〉 triangles 中。

（4）遍历triangles，绘制了每个三角形，并生成名为"delaunay.png" 的PNG 文件。 另外， 代码还将points 和triangles 存储在一个名为"output.obj" 的OBJ 文件中。

2.3 步骤三将划分好的二维网格映射到三维模型

2.3.1 基于朴素反映射算法

二维平面与三维模型子部分存在对应关系， 都过同一个基准法向量， 如果想要找到二维网格在三维模型上的点，直接的方法是通过某一网格结点做一条直线，通过遍历所有三角面片求交点但这计算量无疑太大。

拟用将三维模型投影到二维平面的方法逆向解决上述计算量大的问题， 首先将二维平面上网格结点坐标扩展到三维空间，每个结点Z 坐标都设置为0 即（x，y）转标为（x，y，0）通过将每个三角面片的顶点投影到二维平面上， 以某一网格结点为起始点计算到每个三角面片距离记录下最短距离的对应点， 并从该点去寻找包含该点的三角面片然后做过网格结点且平行于基准法向量的直线与上面找到的三角面片求交点， 而后将求得点的Z 坐标存入到网格结点。

3.2 算法流程

扫描二维平面网格结点建立结点线性表WPointList，建立STL 模型顶点列表SPointList 用于存储顶点投影到二维平面后的坐标， 建立存储三维空间STL 模型子区域三角面片线性表PlaneList 以矩形三角面片为例见图5，表1。

表1 平面网格结点线性表

表2 STL 模型顶点线性表

表3 STL 模型三角面片线性表

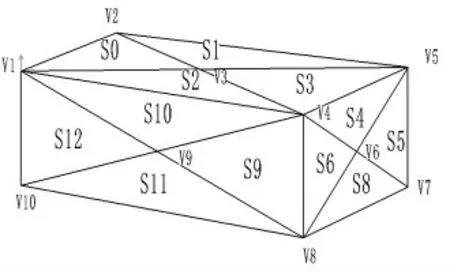
图5 矩形三角面片

遍历表WPointList 将存储的二维坐标扩展到三维，Z 轴坐标为零。

遍历三维模型子部分将坐标存入表SPointList，并将Z 坐标归零。

循环遍历表WPointList直至最后一个坐标值，并进行以下操作。

（1）取出表WPointList 顺序第一值Q 点与表SPointList中的值进行距离计算找到最短的距离对应点的坐标并记为A 点。

（2）遍历表PlaneList，找到含A 点的三角面片，将三角面片存入到ZList。

（3）做过Q 点且并行与Z 轴的直线，与ZList 中的三角面片求交集，将求出的Z 坐标保存到对应Q 点的Z 坐标上。

（4）接着遍历WPointList 取下一个点同样记为Q 点，直至遍历WPointList 所有点。

3 实验

本次进行实验在Windows10 64 位操作系统进行，设备的配置信息：CPU 为i5-8300H，GPU 使用NVIDIA GTX1060， 内存16GB，SSG 为512GB， 实验使用Visual Studio 软件C++语言，使用OpenCV 库展现生成点集和网格，使用Eigen 库进行矩阵和向量计算。

基于第二部分提出的算法思想， 编写了相应的网格生成程序，本节对算法进行实例验证，以圆锥体和正方体为例，模型如图6 和图7 所示，通过限制同一部分三角面片之间法向量夹角， 将圆锥分为了两个子部分分别是锥体和底面圆形，子部分如图6 所示。

图6 圆锥体与划分的子部分

图7 正方体与分割后模型

正方体则被分成了6个面片将模型分开后沿对应法向量进行投影可以保证在一个Z 坐标下不会有两个点，将导出结点存入八叉树数据结构中， 后面使用Opencv 把得到的八叉树点集画出来（图8），并使用Delaunay 三角形法进行平面网格划分， 最终得到子部分进行网格划分后的模型，如图9 所示。

图8 八叉树点集

图9 Delaunay 法划分网格

4 结论

本文基本STL 文件使用八叉树结构对模型进行拓扑重建这一主题进行研究，提出了基于STL 模型分割和重建网格算法， 研究算法中的关键技术，通过Visual studio 实现计算机程序，并进行了简单的实例验证主要工作为提出了一种基于STL 模型文件分割和网格划分算法， 基于每个三角面片法向量夹角大小对整体模型进行分割， 将封闭的模型分割成多个子区域， 再将生成的子区域投影到所选三角面片法向量垂直的平面上， 得到平面点集再将这些平面点集使用八叉树结构储存， 之后使用Delaunay 三角形法进行平面网格划分，最终得到具有拓扑结构的网格模型。