三维网格模型的局部三角剖分算法

李岩席， 贺可太， 朱冬梅

（北京科技大学机械工程学院， 北京100083）

0 引言

利用计算机辅助进行三维模型设计，一直以来是计算机图形领域的核心问题之一。三维网格模型是建立三维模型的一个重要表达方式。Delaunay 三角网格模型在创建地貌模型、逆向工程、表面重建等领域均有广泛的应用。

由于在有限元分析领域中三角网格剖分被广泛应用，所以众多的研究者们对其进行了大量的研究。 20 世纪70 年代初，Lawson 对三角剖分进行研究从而绘制二维流场等值线[2]，Green 和Silbson 等从纯数学的角度对这一问题进行研究[3]。 20 世纪80 年代初，Bowyer Watson 分别提出了Bowyer 算法和Watson 算法[4]。

三角网生长法：Green 等[3]首次实现三角网生长算法，随后被众多学者进行完善。 其算法思想是先任选点集内一点，然后遍历点集寻找距离该点最近的点，并连接这两点作为基边， 接着再根据空外接圆法则寻找第三点形成一个三角形，再以三角形的一边为基边寻找下一个点，最后重复此过程直到点集中全部点搜索完毕形成完整的三角网。 三角网生长算法在遍历点集寻找符合要求的离散点这一步中需要消耗大量的时间， 因此众多学者对三角网生长算法的改进都围绕这一点， 其中最常用的方案为缩小选点范围。 有应用了闭角概念且采用正负区法搜索离散点， 以优先点为中心的Delaunay 三角网生长算法[9]；有提出在寻找第三点时在可选范围内删除封闭点并在外接圆检测时只对距离基边中点最近的n 个点进行检测，封闭点就是在剖分过程中，一个点一旦成为封闭点，则它将不会再对后续的扩展三角形产生影响， 那么将其删除可以有效地提高构建Delaunay 三角网效率。 缩小选点范围还有一个重要手段——对点集进行分区， 有提出弧带搜索排除法将点集划分为若干个弧带， 接着在弧带内进行搜索第三点，缩小了第三点的搜索范围，整体上提高了算法的效率[10]。

分治算法是由Shamos 等[11]首先提出并将其应用到Delaunay 三角网的构网中。随后Lee 等[12]对其进行了改进和完善，提出了分割-归并算法。分割-归并算法的基本思想是将点集分为若干个部分并分别构网， 然后对所构建的网格进行合并。此算法的改进方案分为两种：直接改进合并算法，将分割-归并算法与其他两种方案相结合。 第一种方案可以有效改进算法效率， 改进了算法中最后一步合并算法，通过对点集子集内点的排序，提前确定支撑点范围，减小了搜索范围，有效地提高了算法效率。 虽然分治算法含有大量的递归运算，消耗内存较大，但是其效率高，如文献[13]将分割-归并算法和逐点插入算法相结合，先将点集划分成若干个点集子集，然后利用逐点插入算法生成点集子集Delaunay 三角网， 最后将其合并生成完整Delaunay 三角网，先对点集中的点进行排序，然后分块储存到列表中，接着利用逐点插入法生成子块三角网，最后将链表中的各子网合并， 最终生成完整Delaunay 三角网；吕英英等[14]采取了二叉树结构储存子块三角网，最后将二叉树中父节点相同的子网合并， 最终生成完整Delaunay 三角网。

逐点插入算法，该算法于1977 年由Lawson[15]提出。逐点插入算法的主要思想为首先创建一个大三角形，然后将点集中的任意一点插入大三角形中形成三角网格，再依次将点集中待插入点插入已生成的三角网格中形成新的三角网格， 并对新生成的三角形进行外接圆检测并调整， 待点集中所有点全部插入三角网格后删除和大三角形有相同顶点的三角形，形成最终Delaunay 的三角网。此算法原理简单，但是其时间复杂度较高。因为插入每个待插入点时都需要遍历已构建的三角网， 故许多研究学者对其进行改进， 主要改进方案有两点： 改进点定位算法，对点集分区缩小查找范围。其中第一种方案主要对点定位算法本身进行改进，增加了搜索效率，如对点定位算法直接进行改进[16]，省去了求相交边和三角形重心的步骤，有效地提高点定位效率；文献[17]提出最速方向定位法提高待插入点的插入速度。 第二种方案则是采取了划分点集的手段缩小寻找范围，节省时间，算法效率得到了有效地提升。 例如文献[18]先对待插入点进行排序，将已构网的三角形分区域标记， 从而减少寻找待插入点位置的时间。

约束Delaunay 三角剖分主要需要解决的问题是如何确保在剖分结果中存在应有的约束边和约束面， 通常采取两种方案解决此问题： 第一种方案为先增加剖分点以确保在剖分结果中有应有的约束面和约束边； 第二种方案为先进行Delaunay 三角剖分， 然后将约束面和约束边嵌入Delaunay 三角网中， 这样的后果是约束面或约束边周围的三角形可能不是Delaunay 三角形。

为了保持生成的网格依然保持原三维网格模型几何特征。另外为了尽可能减少新增的节点和三角单元，本文基于Bowyer-Watson 插点算法， 提出一种三维网格模型的局部三角剖分算法。

1 三角剖分算法

在工程应用中， 通常需要从三维空间中的几何曲面生成三维网格。如图1 所示，常见的几何曲面，如平面，柱面，球面，B 样条曲面都是通过二维参数平面映射到三维空间。 所以三维网格模型是在二维参数平面中生成三角网格，再通过参数表达映射到三维空间中。

图1 二维参数平面和三维空间

在二维参数平面上，三角剖分是对给定的平面点集，生成三角形集合的过程。这个过程也称作三角化。对于一给定点集，往往会存在多个三角剖分情况。为避免出现狭长三角形，使三角形形状尽可能接近等边三角形。当所有三角形的外接圆均满足空圆性质的三角剖分， 称为Delaunay 三角剖分。 这时的三角形质量较优，而且有利于数值计算的使用。 三角剖分后生成的Delaunay 三角网是唯一的，并且通过最大化最小角确保接近于规则的三角网。

Delaunay 三角网具有六种优异特性：

（1）最接近性：三角形的三个顶点是点集内最近邻的三个点，且三角形的所有边皆不相交。

（2）唯一性：不论从区域何处开始构建，最终都将得到一致的结果。

（3）最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话， 那么两个三角形六个内角中最小的角度不会变大。

（4）最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay 三角网的排列得到的数值最大。

（5）区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。

（6）具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

Delaunay 三角剖分对三角形的形状进行了定义，具体生成Delaunay 三角网的方法有三角网生成算法、分割-归并算法和逐点插入算法。 其中三角网生长算法理论平均复杂度为O（n3/2），最坏情况为O（n2）；分割-归并算法理论平均复杂度为O（nlogn），最坏情况为O（nlogn）；逐点插入算法理论平均复杂度为O（n3/2），最坏情况为O（n2）。 三角网生成算法是静态算法，只存储新生成的三角形，存储需求较低，但其第三个点需要遍历点集，时间消耗较高。分割-归并算法利用了分而治之的思想，将较大的点集划分为小区域的点集，时间消耗少，但伴随着大量的递归计算，存储需求较高。 逐点插入算法是动态生成的算法，时间复杂度和空间复杂度均不高。 从时间效率和空间使用综合考虑， 所以当前基于逐点插入算法的Delaunay 三角剖分应用较为广泛。 其中Bowyer-Watson 插点算法缩短了搜索坏边的过程，在实际使用中具有更高的计算效率。

本文基于Bowyer-Watson 插点算法， 它是一种逐点插入的方法。首先生成输入点集的初始三角网格，添加节点重新生成新的网格，遍历直到所有的点添加完毕。

Bowyer-Watson 插点算法具体过程为：

Step1：建立初始三角网格：针对给定的点集V，计算得到一个包含该点集的矩形包围盒R。 连接R 的任意一条对角线，形成两个超三角形，作为初始Delaunay 三角剖分T0。

Step2： 将点集V 中的顶点逐一插入现有的三角剖分，现在在它里面再插入一个点P，需要找到该点P 所在的三角形。从P 所在的三角形开始，搜索该三角形的邻近三角形，并进行空外接圆检测。找到外接圆包含点P 的所有的三角形并删除这些三角形，如图2 所示形成一个包含P 的多边形空腔， 叫做Delaunay 空腔。 然后连接P 与Delaunay 腔的每一个顶点，形成新的Delaunay 三角网格。

图2 Delaunay 三角剖分

Step3：删除矩形包围盒R：重复步骤2），当点集V 中所有点都已经插入到三角形网格中后， 将顶点包含辅助窗R 的三角形全部删除。

在每次添加节点时都需要找到该点所在的三角形，确定其所在三角形并删除边构建Delaunay 腔。

2 三角剖分算法改进

在建立Delaunay 三角网格过程中，在原平面区域内插入了新的点，并且打断原有的连接边，建立了新的连接边。

（1）建立包含带剖分区域的大凸壳。

（2）以新插点所在的三角形（或某个被破坏的三角形） 为起始凸腔H。

（3）依次检验凸腔H 的边是否被打断。若被打断，去掉该边，把新找到的三角形的另两条边放到凸腔中；若未被打断，则检验下一个边。

（4）重复步骤（3），直到凸腔H 的所有边均不被打断为止。

（5）连接新点与H 的顶点，形成插点后的网格系统，更新数据结构。

（6）插入下一个点，重复步骤（2）～（4），直到所有点全部被插完。

2.1 数据结构

两种数据结构通常用于实现三角测量算法： 基于边的数据结构，其中最著名的是双连接边表，以及基于三角形的数据结构。 这两种数据结构的共同点是记录表示边或三角形，记录存储指向相邻边或三角形的指针。许多三角测量算法的实现直接读取和更改这些指针。 本方法如表1 所示，通过添加或删除由顶点指定的三角形，以自然的方式访问三角测量。 三角测量存储库完全负责确定三角形邻接关系，并正确维护其内部使用的任何指针。

表1 三角形数据的接口

AddTriangle 和DeleteTriangle 这两个过程通过指定三角形的顶点来创建和删除三角形， 以便存储在数据结构中的所有三角形都具有正方向。 这种数据结构强制执行一个不变量，即一条边只能有两个三角形相邻，而且边的每一边只能有一个三角形。因此，如果数据结构包含一个正向三角形uvw，并且应用程序调用AddTriangle（u，v，w），则三角形uvw 被拒绝，数据结构不会改变。 至少支持两种查询操作。 如果三角剖分包含一个正向三角形uvw，则过程Adjacented （u，v）返回顶点w，否则返回空集。 邻边（u，v）和邻边（v，u）返回不同的三角形，在边uv 的对边。 AdjacentOne（u）识别一个顶点为u 的任意三角形，如果不存在这样的三角形，则返回空集。

2.2 添加三角节点

将输入顶点包围在一个巨大的三角形边界框中，所有的顶点都被插入后，每个有边界框顶点的三角形都会被删除。这种方法的困难之处在于，如果边界框顶点靠得太近，它们可能会在三角剖分中留下凹痕，而且不容易确定它们需要离多远。 计算加权Delaunay 三角化，将三个边界盒顶点的权重赋为负无穷。 这三个无限权值必须是不可比较的，这样包含两个边界盒顶点的测试才能一致地运行。

在点定位过程中。大多数Delaunay 网格生成算法都是在形状不好或超大的三角形的圆内生成新的顶点，在这种情况下，点的位置是自由的。 然而，对于作为网格生成器输入的域顶点来说，点的位置不是自由的。在三角剖分中定位这些点有时是增量插入算法中最耗时和最复杂的部分。本算法，将搜索和连接被打断边所在的点过程限定在局部范围进行。在形成Delaunay 空腔过程中，建立三角形内包含顶点列表，可以更快定位插入点所在三角形。在插入点周围邻域内进行局部的搜索， 这可以提高三角剖分的效率。

Bowyer-Watson 算法只有在新插入的顶点位于三角剖分内时才有效。当顶点位于三角形外部时，在三角形外插入一个顶点。开圆是虚顶点。圆形箭头表示实际上是同一条边的两条虚边。三个虚三角形和三个实三角形（阴影）被删除， 并被两个新的虚三角形和六个新的实三角形所取代。如图3 所示。每个虚三角形的第三个顶点是虚顶点，一个由每个虚三角形共享的“无穷”顶点。 每个虚三角形都有两条虚边与虚顶点相邻。不是虚的三角形称为实三角形。

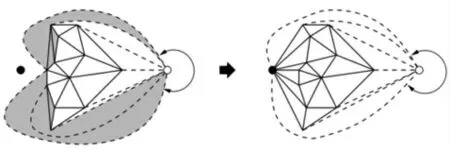
图3 插入点位于剖分三角形外部

本文方法的采样节点都尽可能的遵循原网格的特征，在优化过程中不改变原网格节点的位置，只改变这些节点间连接的拓扑关系。 这样在很大程度上保持原网格的特征。在插入新的三角节点后，破坏的三角单元数目越多，三角剖分计算的性能表现越差。

3 三维网格网格模型的三角剖分

3.1 网格疏密控制

网格疏密控制方法有偏微分方程法、 基网格法和边界驱动法等。 偏微分方程在微分方程中加入了网格疏密控制方法源项的办法来控制网格疏密， 区域内的网格疏密过渡光滑，但此方法计算的工作量较大。网格疏密控制方法边界驱动法则不能够实现区域内部的网格加密和放大，只能实现边界网格尺度向内部平稳过渡。 球填充算法可以生成高质量的网格节点构型。 球填充算法的核心思想是采用小球表示网格节点， 小球的球心表示节点的位置，小球球心的距离对应网格单元的尺寸。通过紧密地填充小球可以生成高质量的网格节点构型。 采用合适的算法连接这些节点可以生成高质量的网格。

在网格疏密控制贯穿剖分过程， 本文基于郭宇飞等的算法[22]，先对网格的特征边界进行识别并采用球填充法在特征边界上采集合适的采样点作为新生成网格节点，然后在模型上其他部分采集合适的采样点添加到新生成网格节点集，最后连接这些节点重生成高质量的网格。

3.2 网格细化生成

在两个边界交叉处出现三角单元三个顶点全在边界的情况， 还有如图4 的狭长针状三角形和帽子三角形。Chew 和Ruppert 优化Delaunay 算法的核心是在质量差的圆周中心插入顶点， 基于Bowyer-Wastons 算法对三角剖分部分增量更新，并保持Delaunay 性质。经过如图5 细化后， 保证三角形一般为圆周与最短边之比大于适当边界B。 Delaunay 插入顶点v 所创建的唯一新边是连接到v的边。 因为v 是某个Delaunay 三角形t 的圆心，而在插入v 之前，t 的圆周内没有顶点，所以没有一条新边可以短于t 的圆周半径。因为t 的圆周与最短边之比大于B，所以每条新边的长度至少是t 最短边的B 倍。

图4 针状三角形和帽状三角形

图5 三角网格的细化

3.3 边界检验

在网格剖分过程中的， 浮点运算产生的计算误差会影响插入点和三角形位置关系的判断， 从而产生错误结果，在计算三角形外界圆半径、圆心坐标和距离时，采用双精度和区域误差来进行逻辑判断。

对于多连通区域， 计算内边界的外法线方向来确定无效的三角形。 为了保证新网格对原网格几何形状的保真度，采用了两个误差度量来评估两个网格之间的距离。边折叠和边分割用于改变网格顶点的数量。 边翻转和顶点重定位提高了网格三角形的质量。 基于区域的网格重划分过程是我们的网格重划分方案的核心， 它产生一个具有高质量三角形和所需顶点采样的网格。 另外两个阶段进一步提高网格质量。 正则化阶段提高了网格连通性的规律性，只留下少量不规则的顶点。 然后，基于角度的平滑在不改变其连通性的情况下对网格进行抛光以获得最佳网格几何形状。

4 实验结果和讨论

我们在C++平台上实现了本三角剖分方法， 所有的实验都是在一台PC 计算机上进行， 它有如下配置：Intel（R） Core （TM） i7-12700H，2.70GHz，16G RAM，NVIDIA GeForce RTX3070 Ti GPU。

如图6 所示，Bowyer-Watson 插点算法在一些多连通区域生成的网格对于如图6（a）内凹的C 形区域，图6（b）中会出现剖分后的三维网格系统不符合原几何形状。 在剖分过程中，需要对网格的边界作进一步的限制。以八个顶点为节点进行Delaunay 三角剖分， 本方法能够进行划分，得到准确的结果。

图6 C 形区域的三角剖分

5 结论

本文提出了一种面向三维网格模型的三角剖分算法， 本文的三角剖分方法基于Bowyer-Watson 插点算法实现。 通过在新插入点的邻域内搜索三角形来提高三角剖分的效率， 通过对网格的几何形状和连通性进行局部修改来提高网格质量。 通过尺寸场来约束控制三角剖分区域， 使得生成的网格质量和算法性能有较好的综合表现。通过实验也能够证明，在多连通的条件下也能够得到正确的结果。