数控技术在农机零部件加工中的优化及应用

裴建军

(新乡职业技术学院(新乡技师学院),河南 新乡 453006)

0 引言

随着农业机械加工及制造行业的迅猛发展,农机零部件的多样化设计需求日益突显。农机作为现代农业生产的重要装备,其性能和质量直接影响农业高效发展。在如此高标准的要求下,传统的加工手段存在低效率、精度不高、能耗大等问题[1-2]。

数控加工利用计算机辅助控制系统,实现了对加工过程的高度自动化和准确控制,通过编程设置加工参数,机床就能按照预定的路径和速度进行精确切削,使得零部件的尺寸和表面质量得到有效保障,不仅可以提高加工精度和稳定性,还可以缩短加工周期,提高生产效率[3]。此外,数控加工采用高速切削和先进的刀具技术,大幅减少切削时间和能源消耗,有利于降低生产成本和减少环境污染。除了高效、精确、节能的优势外,数控节能加工技术还为农机零部件的多样化设计提供了更大灵活性[4]。通过调整程序和工艺参数,可以快速切换加工模式,适应不同零部件的加工需求,从而满足农机多样化设计的要求。

为了进一步提高农机零部件加工的精度及高效,本文基于精英策略的非支配排序遗传算法NSGA-Ⅱ,以农机自由曲面加工为研究对象,对加工的工艺参数进行多目标优化,通过该优化算法,可以在不同的加工参数组合中找到最优解,实现能耗降低和加工精度提高的最佳平衡点。研究结果以期为农机零部件加工提供可持续、高效、环保的解决方案,推动农业机械制造业的技术进步和发展。

1 农机零部件自由曲面类型

自由曲面是指在三维空间中,不受限于特定几何形状或规则的曲面。它可以是任意形状的曲面,不必遵循传统几何形体(例如球体、圆柱体、圆锥等)的限制。自由曲面的形状可以是复杂的,可以是曲线、曲面、曲面之间的连接或过渡曲面等。农机零部件中的自由曲面主要包括初等解析曲面和自由曲面(图1)[5],初等解析曲面是指可以用简单的解析数学公式表示的曲面,具有较为简单的几何形状,如球面、圆柱面、锥面等。自由曲面是指无法用简单的解析数学公式表示的曲面,其形状复杂多变,不受传统几何形体的限制,常用于农机零部件的复杂造型和外观设计,例如机身外壳、罩壳、仪表板等。

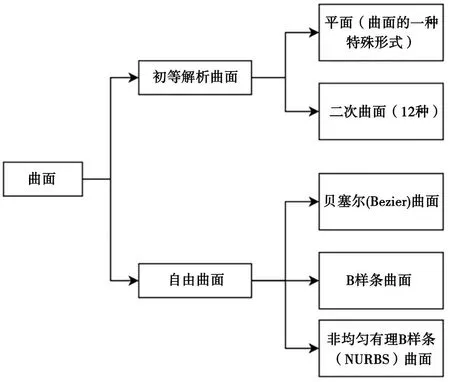
图1 农机零部件常见的自由曲面类型

2 农机零部件自由曲面加工过程火用耗散法建模与能耗评估

热力学第一定律表明,能量不能被创造或毁灭,只能从一种形式转换为另一种形式,而总能量保持恒定,表示能量的转换是一个封闭系统内部的过程,而能量总量在这个系统内不会发生变化。数控加工过程中的能量转换和做功问题,火用理论可以更好地解释能量在加工过程中的转换和利用特性。通过对能量的品质上差别进行量化分析(图2),可以为加工过程的优化和能效提升提供重要参考。

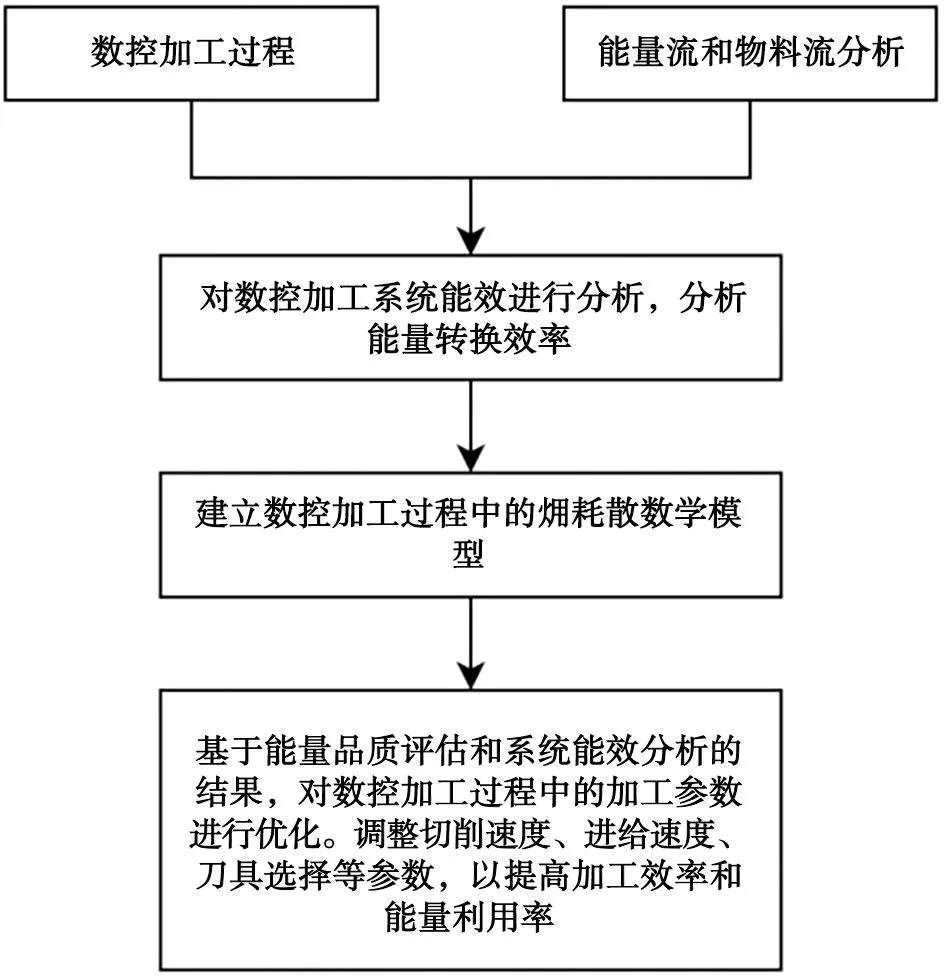
图2 数控加工过程火用理论优化流程

3 基于NSGA-Ⅱ下数控节能加工优化方案

3.1 优化变量

铣削加工参数的选定对零件的主轴转速n、每齿进给量fz、径向切深ae、轴向切深ap,则可以将这4个参数作为优化变量,适当的加工参数能够保证零件加工的精度和表面质量,同时降低能耗,减少热损耗,并延长刀具的使用寿命。优化模型函数如式(1)所示

minEm(n,fz,ae,ap)

(1)

式中Em—铣削加工能耗,kJ。

3.2 NSGA-Ⅱ算法

精英策略的非支配排序遗传算法(NSGA-II)是一种经典的多目标优化算法,用于解决复杂的多目标优化问题。NSGA-II 是对非支配排序遗传算法(NSGA)的改进和扩展,采用了一系列智能化的技术和策略,使其能够更好地应对多目标优化问题,具有较强的全局搜索能力和高效的收敛性,算法执行过程如图3所示,首先从随机生成的初始化父代种群P0开始,利用选择、交叉和变异算子生成子代种群Q0,其种群大小为N个。然后将父代种群P0和子代种群Q0合并形成一个新的种群R0,该种群的大小为2N。

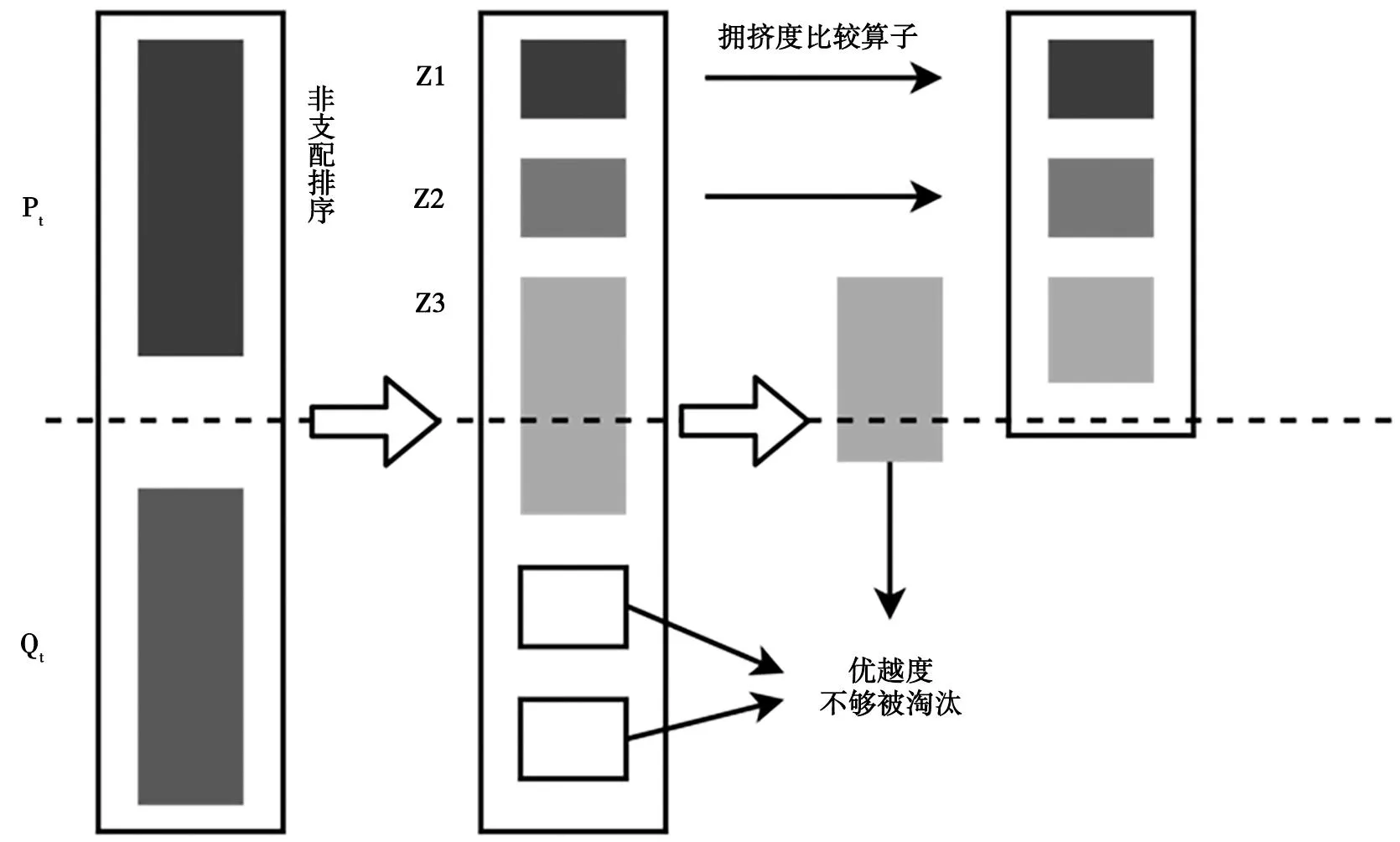
图3 精英策略的非支配排序遗传算法优化过程

接下来,对新种群R0进行非支配排序操作,将其划分为一系列非支配层集Zi(i=1,2…n)。在非支配排序的过程中,会根据个体的支配关系,将它们划分到不同的非支配层次,其中非支配层次越小的个体越优秀。

然后,对于每个非支配层集Zi,计算各个个体之间的拥挤度,衡量个体之间的分布情况,通过维护个体间的多样性,有助于保持种群的多样性和均衡性。接下来,从非支配层集Z1中选择个体,并将这些优秀个体放入新的父代种群P2中。如果现在的父代种群P2的大小还没有达到N个,系统会继续将下一个级别的非支配层集Z2中的个体加入父代种群P2,以此类推,直到种群P2的规模达到N个为止。

对于超出N个的非支配层集Zm,需要使用拥挤度比较算子来决定保留哪些个体。拥挤度比较算子根据个体在非支配层集中的拥挤度值,对优越度进行降重,从而保留最优秀的个体,并淘汰其他个体,以保持种群的多样性和高质量解的存留[6-8]。

3.3 基于NSGA-Ⅱ算法下非支配排序

在NSGA-II算法中,非支配排序是其核心步骤之一。非支配排序是将候选解根据其在多个目标函数上的优劣进行排序,划分成不同级别,使得在同一级别的解彼此之间没有支配关系,从而找到较优解的集合。

3.4 Pareto解集

通过非支配排序后,种群中的个体将被划分为多个不同的非支配层级,其中每个层级的个体之间相互没有支配关系。在非支配排序过程中,个体根据其在多个目标函数上的优劣进行排序,优于其他所有个体的为第一层,优于除第一层之外的所有个体的为第二层,依此类推。

通过非支配排序,可以得到一组较优的解集,这些解在不同目标上取得相对均衡的性能,形成一个称为“帕累托前沿(Pareto)”的解集。为了保证个体在帕累托前沿上均匀分布,NSGA-II算法引入了拥挤度计算。拥挤度是衡量个体在目标空间上的密度,用于衡量个体之间的相对距离。通过拥挤度计算,算法可以更好地维持帕累托前沿上的多样性,使得优秀解集更加丰富和分散。计算公式如式(2)所示

(2)

式中id—i点的拥挤度;

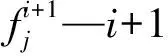
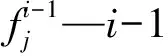
4 参数优化及试验研究

4.1 试验设计

本文以常见的45号钢为加工材料,加工参数优化范围如表1所示。

表1 加工参数优化范围

4.2 加工工艺参数优化

本文使用MATLAB 2018实现基本的NSGA-II算法框架,参数设置如表2所示。

表2 NSGA-II算法参数设置

运行 NSGA-Ⅱ算法进行帕累托前沿求解过程及结果如图4所示,目标函数1表示能耗,目标函数2 表示加工温度,图中虚线框表示最优解范围。结果表明,优化后的最优加工参数分别为主轴转速n=2 398 r/min、每齿进给量fz=0.222 mm/r、径向切深ae=3.97 mm、轴向切深ap=0.2 mm,铣削加工能耗Em=54.23 kJ。

图4 NSGA-Ⅱ算法的 Pareto求解

5 结论

本文应用了数控节能加工技术在农机零部件加工中的应用,通过精密的计算机控制,实现了对农机零部件加工过程中各个参数的准确控制。针对传统农机零部件加工过程能耗大以及难以控制的问题,基于带精英策略的非支配排序遗传算法NSGA-Ⅱ进行了多目标优化,并进行了实验对比分析。

试验结果表明,采用NSGA-Ⅱ算法优化切削加工参数能够显著提高农机零部件加工的能效和性能。通过对切削加工参数主轴转速、每齿进给量、径向切深和轴向切深进行优化获得了一系列优质的非支配解,优化后的参数组合不仅能够降低能耗,还能够保证加工质量和刀具寿命的提高,实现了零部件加工的高效、精确和节能。