基于改进麻雀优化PID的波浪补偿控制方法
张 琴,蔡慧茹,兰明东,浦 克,胡 雄
(上海海事大学物流工程学院,上海 201306)
在“双碳”目标以及海上风电“十四五”规划的推动下,沿海各省相继开展了海上风电机组的研发与安装工作,14~16兆瓦级的大型海上风机相继问世。其不断增大的规模以及在吊运、安装过程中海浪对船舶产生的持续影响,都会导致安装的精度和效率大幅下降,甚至会对人员安全以及财产带来重大损失[1–2]。因此,如何在工程船上提供一个稳定的环境,以保证各项作业高效、高质量地完成成为了一个有价值的研究课题。
建立补偿机构及模型是进行优化控制的基础,补偿机构的模型可以根据控制力执行方式的不同分为被动式补偿和主动式补偿[3–4]。被动式波浪补偿主要是根据已有的受力变化来控制补偿参数,属于单自由度的恒力补偿,不需要消耗动力,但精度低并且存在较大滞后[5–6];主动式波浪补偿是通过传感器获得船舶位姿,进而求解得到补偿所需要的驱动力信号,最终通过控制器执行来达到补偿效果,其在模型设计、补偿精度以及响应速度上都要优于前者,满足复杂海况下海洋作业的需求[7–8]。对于主动式波浪补偿,胡永攀等[9]提出一种基于绳牵引并联机构的波浪补偿结构,在弱干扰下达到了较好的控制效果,然而在复杂海况下,该结构不能够很好地控制精度,且其部署在起重机末端,难以提供足够的承重区域进行风机的吊运安装工作。对此,梅江平等[10]提出了3–SPR(three–spherical paral lel robot)补偿结构,该结构可安装于甲板上,弥补了空间不足的缺陷;并通过实验验证了该结构的正确性和可行性。随后,詹勇等[11]对此结构进行了优化,并采用规则波进行4级海况下的仿真实验,结果表明,该设备在此波形下可以保证足够的响应速度和控制精度,但3个支链是平行分布,在强度和稳定性上存在一定的不足。Salzmann等[12]提出一种6自由度补偿平台(Stewart平台)结构,并验证了其可行性。通过控制6个支链伸缩,基于其耦合关系达到控制上平台位姿转变的目的,可以进行全自由度补偿。针对此结构研发出的设备在刚度、承载力及稳定性等方面都颇为优秀,被广泛应用在航天、海洋作业及制造业等领域。根据Stewart平台的机械结构及传动模式建立动力学模型,该模型可以更好地表示平台运动与各驱动单元输入力的关系。
在模型建立的基础上,波浪补偿控制方法的选择也成为影响最终控制效果的关键因素。李世振等[13]在单自由度升沉运动补偿的研究中使用了鲁棒、滑模等智能控制,取得了不错的控制效果,但在复杂海况下,仅单自由度补偿不足以提供稳定的作业环境。苗梦亮[14]基于广义预测控制(MPC)对主动式波浪补偿进行控制,研究达到不错的效果,但MPC过于依赖模型,不适合复杂多变的对象,且优化过程是比较耗时的,在实际工作中可能会带来较大的滞后[15–16]。Zinage等[17]提出了一种基于强化学习(RL)的控制器,采用深度确定性策略梯度算法(DDPG)对单自由度进行主动升沉补偿,取得了很好的效果,但学习过程耗时较长且存在振荡。
中国在波浪补偿领域还处于研发阶段,在模型已知的情况下,可靠性高、过程简化的PID控制器仍是实际应用中的研究热点。针对波浪补偿平台而言,PID控制器参数的整定是控制效果的关键,因此,将优化算法与PID控制器结合进行优化控制。周明建等[18]对波浪补偿系统的PID参数使用遗传算法(GA)进行优化,获得较好的控制精度和抗干扰能力,以此证明该方法的准确性。唐刚等[19]建立了波浪补偿平台单通道模型,并使用粒子群算法(PSO)对PID控制器参数进行整定优化,结果表明,优化得到的参数可以起到不错的效果。上述研究为波浪补偿系统的优化控制提供了可行的方向,但没有结合整个波浪补偿平台,因此,无法验证最终补偿的效果;并且,针对PID控制器参数范围大的特点,现有的优化算法并没有采用跳出局部最优的策略。为此,薛建凯等[20]提出麻雀搜索算法(SSA),该算法在精度、收敛速度及鲁棒性方面较遗传算法、粒子群算法等都有了一定的提升。随后,针对SSA易陷入局部最优的问题,t分布变异策略、基于差异的局部搜索和动态自适应加权等方法被应用到SSA中,在全局寻优能力及收敛速度方面较原算法都取得了较大的提升[21–23]。
从提高收敛速度及增强全局寻优能力的角度出发,本文提出一种改进麻雀搜索算法,即结合circle混沌映射、动态加权、柯西突变和反向学习策略的麻雀搜索算法(circle cauchyreverselearningbased sparrow search algorithm,CCRSSA),并将其应用于波浪补偿平台PID控制器参数的整定中。首先,根据Stewart结构建立了Stewart平台动力学及运动学反解模型;随后,使用麻雀搜索算法对PID参数进行整定优化,并在麻雀搜索算法中引入circle混沌映射、动态加权及柯西突变和反向学习策略,提高了算法对参数的优化能力;最后,生成PM谱下4~6级海况的工程船运动数据,比较了在数据集下GA、PSO、SSA等方法对PID参数的优化效果,结果表明,改进麻雀搜索算法能够较好地应用于波浪补偿平台的优化控制。
1 波浪补偿平台
1.1 波浪补偿平台介绍
本文使用Stewart平台作为研究对象,图1为Stewart平台的实物图。在Simulink软件中使用SimMechanics工具集,根据Stew art平台的机械结构及传动模式建立动力学模型,将上、下层分别作为波浪补偿系统和船舶运动模拟系统,相邻平台间由6个电缸驱动的支链连接支撑,平台与支链由虎克铰连接,通过对6个支链进行控制,可以使平台实现6个自由度位姿的运动,包括:横摇、纵摇、艏摇、横荡、纵荡及升沉,其中,横荡、纵荡、艏摇都可以借助船舶自身的动力定位或者锚泊技术实现补偿[24–25]。故本文仅对横摇、纵摇、升沉运动进行控制补偿,其中,升沉运动会引起货物与甲板的碰撞,横摇和纵摇则是造成设备摇晃的主要原因[26]。因此,补偿升沉、横摇、纵摇这3个自由度上的运动是实现海上安全作业的关键技术。

图1 Stewart波浪补偿控制平台Fig.1 Stewart wave compensation platform
1.2 波浪补偿原理
图2为补偿系统模型设计波浪补偿控制策略。首先,将生成的工程船3自由度运动信号输入船舶运动模拟系统,以此来模拟船舶运动;通过正解模型对船舶运动模拟平台进行反解计算,求得使补偿平台保持稳定的6个支链位移,作为波浪补偿系统的参考输入,同时,根据编码器检测到的支链实际位移,采用PID进一步控制6个电缸;随后,根据编码器采集到的实际位移,通过正解模型求解补偿平台3个自由度,验证其稳定性。下面对波浪补偿系统模型进行分析计算。

图2 波浪补偿控制示意图Fig.2 Wave compensation control schematic
2 波浪补偿系统模型
2.1 平台位姿分析
对Stewart平台进行正反解分析,需要6个参数建立平台坐标系:波浪补偿系统上平台外接圆半径r及偏转角a、下平台外接圆半径R及偏转角b、基准位上下平台垂直距离h及此时支链初始长度l0。将图1中波浪补偿系统的下、上平台分别作为动平台(Base)和静平台(Platform),以其中心OB、OP为原点分别建立两个坐标系:动坐标系OB-XBYBZB,静坐标系OPXPYPZP,两个坐标系如图3所示。其中,静平台偏转角a=(∠P1OPP6)/2,绞点P1~P6为静平台与支链连接点;动平台偏转角b=(∠B3OBB4)/2,绞点B1~B6为动平台与支链连接点。
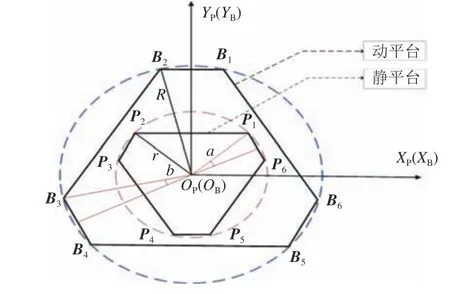
图3 波浪补偿系统的平台坐标系Fig.3 Platform coordinate system for wave compensation system
由图3可得静平台各铰点Pi(i=1,2,···,6)在静坐标系中的坐标,以及动平台各铰点Bi在动坐标系中的坐标,分别以P1和B1为例表示如下:
求得坐标后,通过坐标旋转矩阵进行反解计算。
2.2 运动学反解模型
当动平台绕XB轴、YB轴、ZB轴做横摇、纵摇、艏摇运动时,可通过坐标旋转矩阵将动坐标系中的点在惯性坐标系中表示出来,其中,惯性坐标系以图1中基座外接圆圆心为原点建立,从而进行同一坐标系下的运算,其中旋转矩阵T可以表示为:
式中,s为正弦,c为余弦, α为横摇角度, β为纵摇角度,γ为艏摇角度。通过将加速度计、陀螺仪检测到的船舶运动模拟平台3自由度信号带入,可求得动平台在做横摇、纵摇以及升沉复合运动时,其绞点在惯性坐标系中的坐标为:
式中,B0=[0 0Z+h]T,其中,Z为升沉引起的动平台高度位移值,h为Stewart平台处于中间(home)位置时的上下平台垂直距离。而补偿平台目的是保持稳定,因此,其绞点坐标固定,绞点在惯性坐标系中坐标如下:
此时,波浪补偿系统6个支链(第i个绞点对应第i个支链)的长度向量l i在惯性坐标系中可表示为:
并可由长度向量求得支链位移 ∆ls:
式中,||l i||2为对l i进行2范数求解,为第i个支链的初始长度,最终, ∆l i作为图2所示的波浪补偿系统控制器的输入信号。
综上,当已知Stewart平台的尺寸和位姿时,通过式(3)~(6)求解出6个支链位移的过程即为运动学反解。通过运动学反解,求得使补偿平台保持稳定时波浪补偿系统6个支链的位移,作为补偿控制参考输入。
2.3 正解模型迭代求解
正解模型用于对补偿平台的稳定性进行验证。通过编码器测得的补偿系统6个支链位移,求解其3自由度的过程称为正解。求解方程如下:
式中,γ1、α1、β1分别为运动轨迹中初始时刻的升沉位移、横摇角度、纵摇角度,Ui(α1,β1,γ1)′为波浪补偿系统第s个支链位移求解值,Ei(α1,β1,γ1)为波浪补偿系统第s个支链位移求解误差,F为对6个支链位移求解误差求和,di为编码器采集到的第i个支链的实际位移,Ei为第i个支链的位移求解误差。通过将上一时刻3自由度求解结果作为该时刻初始值,分别带入下列公式中进行迭代:
式中,k1、k2、k3分别为升沉、横摇和纵摇运动的迭代步长,可根据不同海况等级进行设定,Rand(0,1)为0和1之间的随机数。求得在F最小时的解,以此获得补偿平台3自由度。该算法流程图如图4所示。
设定迭代次数上限kmax,k为迭代项数,F(k)为第k次迭代后的误差,当进行kmax次迭代后没有更优解出现时,输出当前α、β、Z作为最优解,并将此解作为下一时刻初始值。设置不同的上限可以实现不同精度的求解,通过以上算法解决连续运动轨迹下的正解模型求解问题[27]。
对船舶运动模拟系统进行上述算法求解,将结果与传感器采集到的信号进行比对来验证算法的可行性。在动力学及正反解模型建立后,对波浪补偿系统的6个支链进行PID控制。
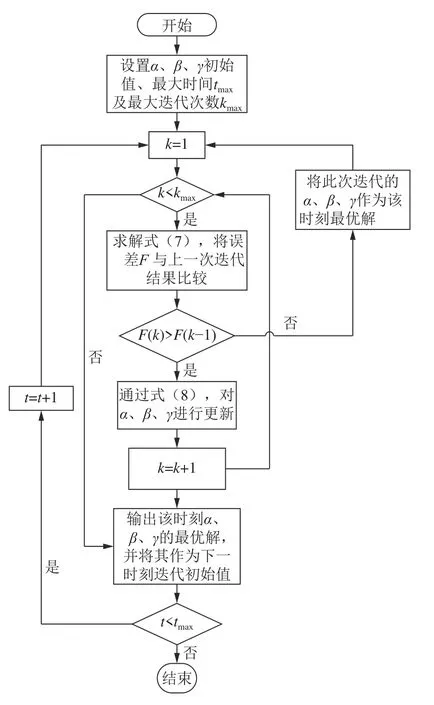
图4 正解模型迭代求解Fig.4 Iterative solution of the positive solution model
2.4 正解模型的求解验证
海况是指风力影响下的海面状况,可进行海上作业的最高海况等级为6级,故本文选择在4~6级海况下进行仿真实验。其中,PM谱是一种长期观测得到的海浪频谱,符合广阔海域下工程船舶的作业环境,因此本文选择用其生成4~6级的海浪运动。考虑到船舶和海水的边界关系,选用基于势流理论计算浮式结构水动力学特性的Ansys–AQWA软件,通过将船模置于4~6级海况下得到对应的船舶运动,进而控制补偿平台,验证其稳定性,图5为使用的工程船模型示意图。

图5 某工程船模型示意图Fig.5 Schematic diagram of an engineering ship
针对风机安装等大型海上作业的某工程船模型船舶主尺度见表1。

表1 船舶主尺度Tab.1 Vessel master scale
通过正解模型对船舶运动模拟平台进行3自由度求解,进行求解效果验证,结果如图6所示。
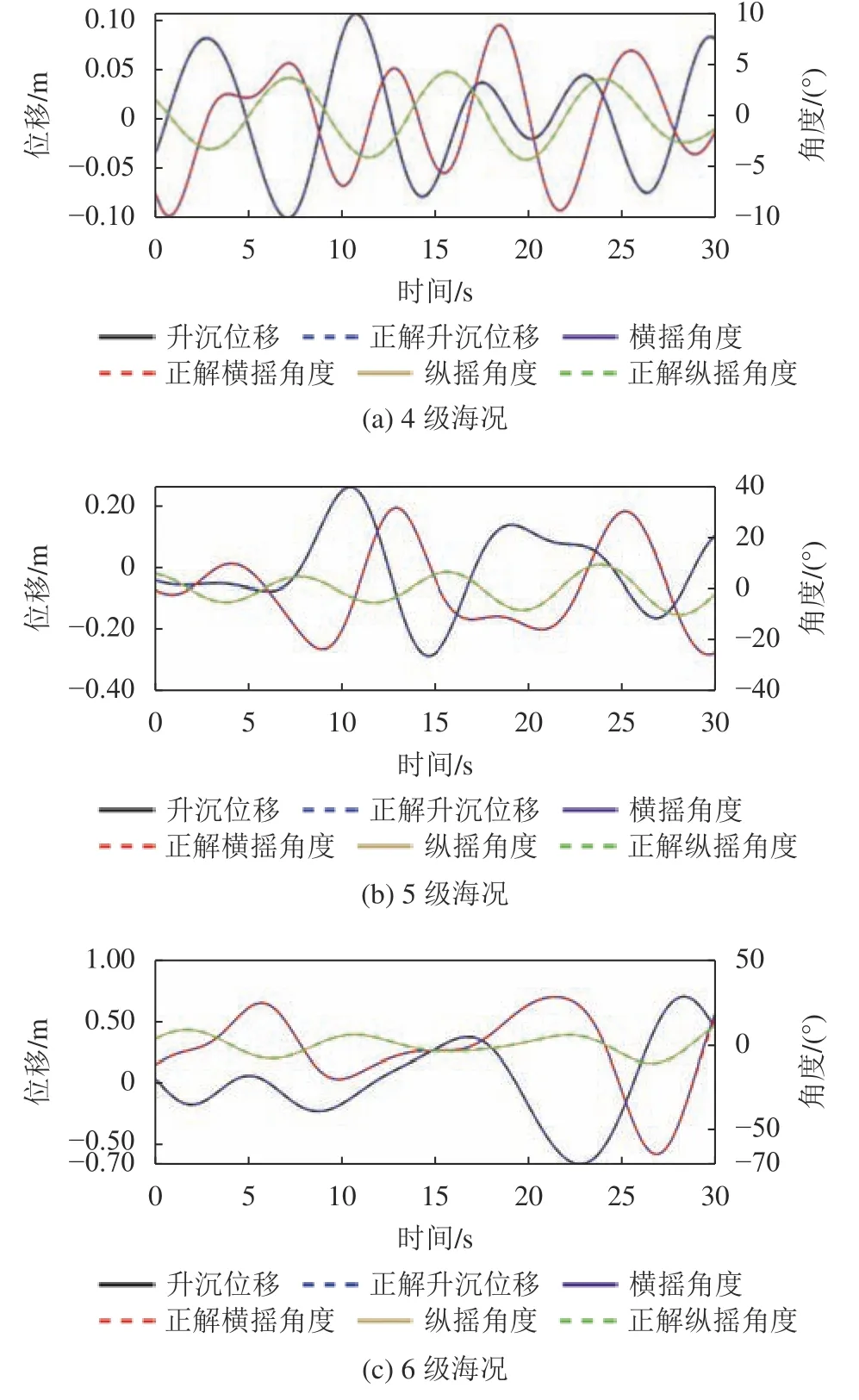
图6 4~6级海况下的船舶运动Fig. 6 Ship movemnt from sea state four to six
从图6中可以看出,算法求解结果与检测到的工程船运动基本吻合,验证了求解算法的可行性,用于后续对波浪补偿系统的正解模型求解。
3 控制及优化方法
3.1 PID控制
将反解得到的波浪补偿系统6个支链位移作为参考输入,在与编码器检测到的实际位移做差的基础上,对波浪补偿系统的6个支链进行PID协同控制:
式中,ei为波浪补偿系统第i个支链的位移误差,、pi分别为第i个支链参考位移及编码器检测到的第i个支链实际位移,为输入给第i个支链的驱动力,t为连续运动轨迹时长,KP、KI、KD为比例、积分、微分系数。
通过PID对支链位移信号进行求解,获得驱动信号,其3个参数决定着控制性能但又难以确定,故使用麻雀搜索算法对其进行整定。基于式(8)中的位移误差,构建时间绝对误差积分(ITAE),记为EITA,作为优化算法的适应度值函数,如式(10)所示:
3.2 麻雀搜索算法SSA
麻雀种群中包含发现者、跟随者和警戒者3种麻雀,其不同个体之间会相互监视。发现者指获得了更好食物来源的麻雀,跟随者通常会夺取发现者同伴的食物,而一部分麻雀会作为警戒者警惕天敌的到来,基于此来模拟麻雀觅食的过程。
在进行比例积分微分控制器参数优化时,优化变量为KP、KI、KD3个参数,因此算法的解空间为3维。若存在N只麻雀[,则第m]只麻雀在3维解空间中的位置为X m,X m=,其处于上下限[bl,bu]之间,表示第m只麻雀在3维解空间中的比例增益、积分时间、微分时间的参数值。在每次迭代后,都会根据种群中不同麻雀的适应度值,按照从高到低进行排序,并选择适应度值较低的后20%的麻雀作为发现者,其余麻雀作为跟随者,分类完成后再从所有麻雀中随机选取10%~20%的麻雀作为警戒者,用于防止陷入局部最优。
发现者为了获得更低的适应度值,要进行的位置更新如下:
跟随者则按照当前位置a与中间位置N/2间的大小关系,向最优或者最差区域移动来获得更低的适应度值,其位置更新公式为:
同时在整个种群中选择一定比例的麻雀作为警戒者,其不论当前位置好坏,都会移动到一个新的位置:
每次迭代后不同麻雀会基于适应度值高低在发现者和跟随者之间转化,但发现者和跟随者在种群中所占比例是固定的。基本麻雀搜索算法在PID参数初始化时较大的随机性会导致分布不均匀,进而降低后期迭代寻优能力;此外,在进行位置更新时容易陷入局部最优,错过其他最优解,针对这两点问题做出如下改进。
3.3 麻雀搜索算法的改进
1)改进的circle混沌映射初始化混沌映射具有分形的特征,可以在对麻雀位置进行初始化时产生更均匀的分布效果,以此来获得较好的初始值[28]。这里选用效果稳定且初始化分布均匀的circle混沌映射:
式中,Ym,j为第m只麻雀在第j维的比例系数,mod为模运算,Xm,j为混沌映射初始化后的麻雀位置, ⊕为矩阵点乘运算。
2)动态自适应加权更新发现者
在前几代中,发现者会更趋向于局部最优解,导致寻优范围小、寻优能力不足。因此,引入权重系数α,在迭代初期较大的权重会增加搜索范围,提高寻优能力,在末期较小的权重可以增强算法的深入开发能力,将式(11)更新为:
式(15)~(16)中, α为权重系数。
3)改进警戒者更新模式
为了扩大寻优范围,不局限于当前最优解,对警戒者进行改进,将式(13)改为:
警戒者会根据当前适应度值,在最优、最差以及目前位置之间进行搜索。
4)结合柯西突变和反向学习策略
为了防止陷入局部最优,提升算法的全局寻优能力,在每代麻雀更新结束后加入了柯西突变与反向学习选择策略。柯西突变来自于柯西分布,柯西分布公式如下:
式中:f(x)表示柯西分布的概率密度函数;x为柯西分布随机变量,其生成函数为x=tan[(ζ-0.5)],其中ζ ∈(0,1)。
以标准柯西分布为基础,在麻雀更新中引入柯西突变,提高算法的全局优化能力:
将求得的f(x)代入式(19)中,以此得到经过柯西突变后的麻雀位置。
反向学习策略通过计算当前解的反向解,以增大寻优范围,过程如下:
柯西突变可以使算法跳出局部最优解,而反向学习可以增强全局寻优能力,为了进一步改进算法的优化能力,通过引入概率Ps做出决定:
式中, θ为用于调整概率偏移率的参数,设置为0.05。
通过生成随机数Rand与Ps进行比较,概率选择策略如下:
1)如果Ps>Rand,选择反向学习策略更新;
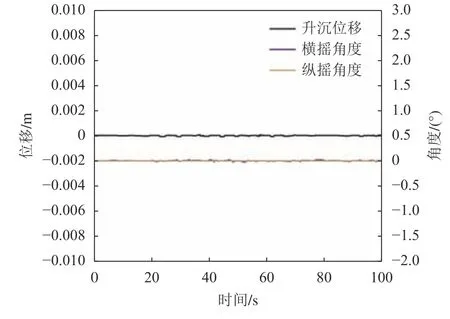
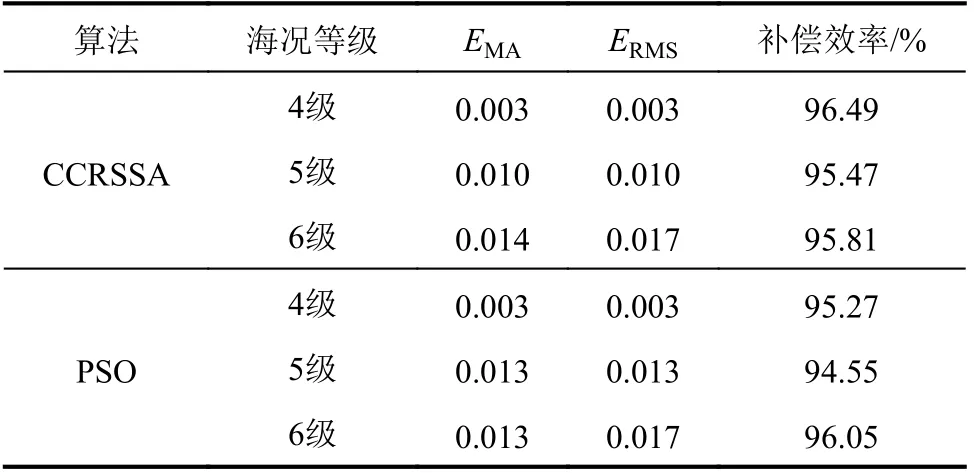
2)如果Ps 3)更新前后的结果进行比较,保留最优值。 本文提出的改进麻雀搜索算法CCRSSA流程图如图7所示。 图7 改进麻雀搜索算法流程图Fig.7 Improved sparrow search algorithm flow chart 改进麻雀搜索算法CCRSSA流程的步骤为: 1)设置种群数量、变量上下限、种类占比等参数,使用circle混沌映射进行初始化; 2)计算每只麻雀的ITAE值作为适应度值,按照从低到高排序并进行分类; 3)根据式(16)、(12)和(17)进行发现者、跟随者和警戒者的位置更新; 4)根据式(23)中的结果,进行柯西突变和反向学习策略的选择及更新计算,并对比更新前后的适应度值,保留较低适应度值对应的解; 5)判断是否满足结束条件,否则跳转步骤2),满足则结束,得到经过算法优化后的KP、KI、KD参数。 使用上述算法优化得到的PID参数进行控制,进行3自由度补偿稳定性验证: 使用MATLAB和Simulink软件进行优化控制仿真,经过多次实验为基础,设置种群规模为10,最大迭代次数为10,分别在4、5、6级PM谱海况下及浪向角为90°和180°的重力波下比较circle混沌初始化、circ le混沌初始化+动态自适应加权更新发现者、circle混沌初始化+动态自适应加权更新发现者+警戒者更新、CCRSSA算法的优化PID的波浪补偿效果,以上算法在不同条件下的EMA和均方根误差(ERMS)见表2。 表2 不同海况下不同浪向角的补偿方法效果对比Tab.2 Comparison of the compensation method effects 表2结果表明,不论是在PM不规则波下的4~6级海况中的船舶运动,还是规则重力波的不同浪向角的6级海况下的船舶升沉,每步改进策略优化PID控制后的补偿精度都在不断提高,而且CCRSSA的EMA和ERMS的值最小,验证了改进后的麻雀搜索算法比基本麻雀搜索算法对PID具有更好的优化效果,适用于不同浪向角下的复杂海况。 为了更好地验证CCRSSA的优化控制效果,在每级海况下分别对比了遗传算法GA、粒子群算法PSO、麻雀搜索算法SSA及基于混合策略的麻雀搜索算法(HSSA)的优化效果,5个方法在4~6级海况下的适应度值如图8所示。 图8 不同算法的适应度值迭代结果Fig.8 Optimization results of different algorithm fitness values with iterations 由图8可知:在引入circle混沌映射初始化策略后,CCRSSA较SSA在初始化阶段有较大提升,可以加快后续寻优速度;此外,在不同海况下,CCRSSA始终可以在相同迭代次数内取得最小适应度值,使平台实现更精确的跟踪;另外在4、6级海况下,改进的麻雀搜索算法在第4次迭代中基本可以达到最优,在5级海况下的第6次迭代中也基本达到最优。4~6级海况下各算法的ITAE收敛结果比较见表3。 表3 各算法ITAE收敛结果Tab.3 Convergence results of ITAE for each algorithm 通过对比表3数据可知,CCRSSA的ITAE指标在5种算法中最小,可知其控制精度最高。在4级海况下,相比于PSO和SSA,CCRSSA的ITAE分别减小约15.2%和4.3%;在5级海况下,较PSO、SSA减小约0.3%;在6级海况下,较PSO和SSA减小约2.2%。综合收敛速度和收敛精度,CCRSSA表现要比GA、PSO、SSA及HSSA更优异。 表4为使用CCRSSA优化得到的PID参数,将参数带入模型中进行4~6级海况下的仿真实验,通过正解模型求解式(7),将得到的运动模拟平台3自由度位姿与传感器采集到的位姿数据做差后,获得补偿平台3自由度补偿结果,以6级海况为例说明,图9为6级海况优化后补偿平台稳定性效果验证。其中,纵坐标为补偿平台在3个自由度上的运动,目标是保持为零。 表4 CCRSSA优化的PID参数Tab.4 CCRSSA optimization of PID parameters 图9 6级海况优化后补偿平台稳定性验证Fig.9 Optimized compensation stability validation 从图9可以看出:在起始阶段,由于KP、KI较大的原因,会产生一个较大的波动,但在2 s内会消除;在之后的时间内,补偿平台在4~6级海况下的6个自由度基本都保持在0附近。 结合算法优化结果及最后的补偿效果,证明了在4~6级海况下,CCRSSA算法要更适用于波浪补偿平台的优化控制,可以提供稳定的作业环境,满足复杂海域下长时间、高精度的海上作业要求。 强化学习具有模型无关性,在波浪补偿控制中,海洋环境通常非常复杂且难以建模,强化学习可以通过与环境的交互来直接学习最优的波浪补偿策略。但是,强化学习的性能很大程度上依赖于奖励函数的设计,同时,需要进行大量的训练和学习,使得其需要大量的样本数据,且训练过程相对较长。图10为6级海况下3自由度的补偿控制方法效果对比,表5为6级海况下PID和强化学习控制误差对比。由图10和表5可知,在第6秒之前,强化学习并没有及时对船舶运动进行补偿控制,而在第6秒之后补偿误差逐渐减小,其ERMS为0.005 4。而PID控制可以对船舶运动做到很好的补偿,ERMS达到4.969 2×10-4。相比之下,PID控制具有实时响应的优势。 图10 波浪补偿控制方法效果对比Fig.10 Comparison of wave compensation control 表5 波浪补偿控制方法误差对比Tab.5 Comparison of error 使用图1所示的实验室硬件设备进行试验,硬件主要包括控制台以及波浪补偿平台部分,其各部分之间的关系如图11所示。 首先,上位机通过通讯协议将数据指令发送给控制器,由控制器读取指令后转换为脉冲控制信号发送给6个伺服驱动器;然后,通过其控制对应的伺服电机运行;最后,通过丝杆等装置将其转化为电动缸相应的位移。通过6个电动缸之间的协同运动,来表现平台的自由度变化,同时通过伺服电机固定的编码器对电机进行转数测量,计算后得到电动缸位移。 图11 波浪补偿平台控制原理图Fig.11 Wave compensation platform control schematic 为了验证本文方法的适用性和泛化性,在4~6级海况下选取与第4.2节仿真数据的波高、周期都各不相同的数据,生成新的4~6级海况下的船舶运动数据,其波高、周期数据见表6。 表6 船舶运动数据的波高和周期Tab.6 Wave height and period of ship motion 然后,使用AQWA软件重新生成船舶在该波高和周期下的3自由度运动数据,以6级海况为例,船舶运动如图12所示。 图12 6级海况下对比实验船舶运动数据Fig.12 Comparison of experimental ship motion data under sea state 6 对以上船舶运动数据分别使用CCRSSA和PSO优化后的参数进行波浪补偿试验,对采集到的电动缸长度数据进行正解计算,求得3自由度补偿结果,以6级海况为例,CCRSSA和PSO控制实验结果如图13、14所示。 图13 CCRSS在6级海况优化控制试验结果Fig.13 CCRSSA optimized control test results 图14 PSO在6级海况优化控制实验结果Fig.14 PSO optimized control test results 进行补偿误差以及补偿效率的计算,4~6级海况下CCRSSA和PSO的对比结果见表7。 表7 优化控制试验补偿误差及补偿效率对比Tab.7 Comparison of compensation error and compensation efficiency for optimal control tests 对表7中的补偿误差和效率进行分析。首先,在6级海况下,CCRSSA的优化补偿效率稍低于PSO约(0.2%),与其优化得到的KD参数较小、波动稍大有关,这使EMA误差仅增大了0.001。其次,CCRSSA优化得到的参数在4级和5级海况下补偿控制中的补偿效率要比PSO分别高1.22%和0.92%。故综合3种海况来看,CCRSSA在不同海况下的补偿控制结果具有优势,虽然随着海况等级的增加,其补偿效率稍有下降,不过都达到了95%以上,可以满足高精度波浪补偿的需要。 本文以波浪补偿平台为研究对象进行主动式波浪补偿研究。首先,建立Stewart平台动力学及反解模型,并基于随机搜索设计正解模型求解算法,同时基于某工程船在PM谱下4~6级海况的运动姿态在补偿仿真平台进行正解求解验证;然后,用PID对其进行控制,并使用麻雀搜索算法优化参数;随后,提出一种改进麻雀搜索算法用于优化控制,通过circle混沌映射、动态加权、柯西突变及反向学习策略改进算法寻优效果。接下来,基于某工程船在PM谱下4~6级海况的运动姿态进行补偿仿真和硬件平台控制验证。基于PM谱下的4~6级海况和6级海况下浪向角为90°和180°的重力波,对改进麻雀搜索算法做了消融实验,验证了CCRSSA对PID控制的参数优化具有更好的效果。最后,基于补偿仿真和硬件平台,与强化学习控制方法对比证明了PID控制可以对船舶运动做到更好的补偿,具有实时响应的优势。并与GA、PSO、SSA、HSSA的优化效果进行比较,结果证明了CCRSSA在4~6级不同海况下都具有良好的优化控制效果和收敛速度,能较好应用于船舶波浪补偿控制中,可以对以后相关方面的研究提供一定的参考,后续可以研究应用于多种海况下的自适应模型,并以此为基础设计在线补偿控制方案。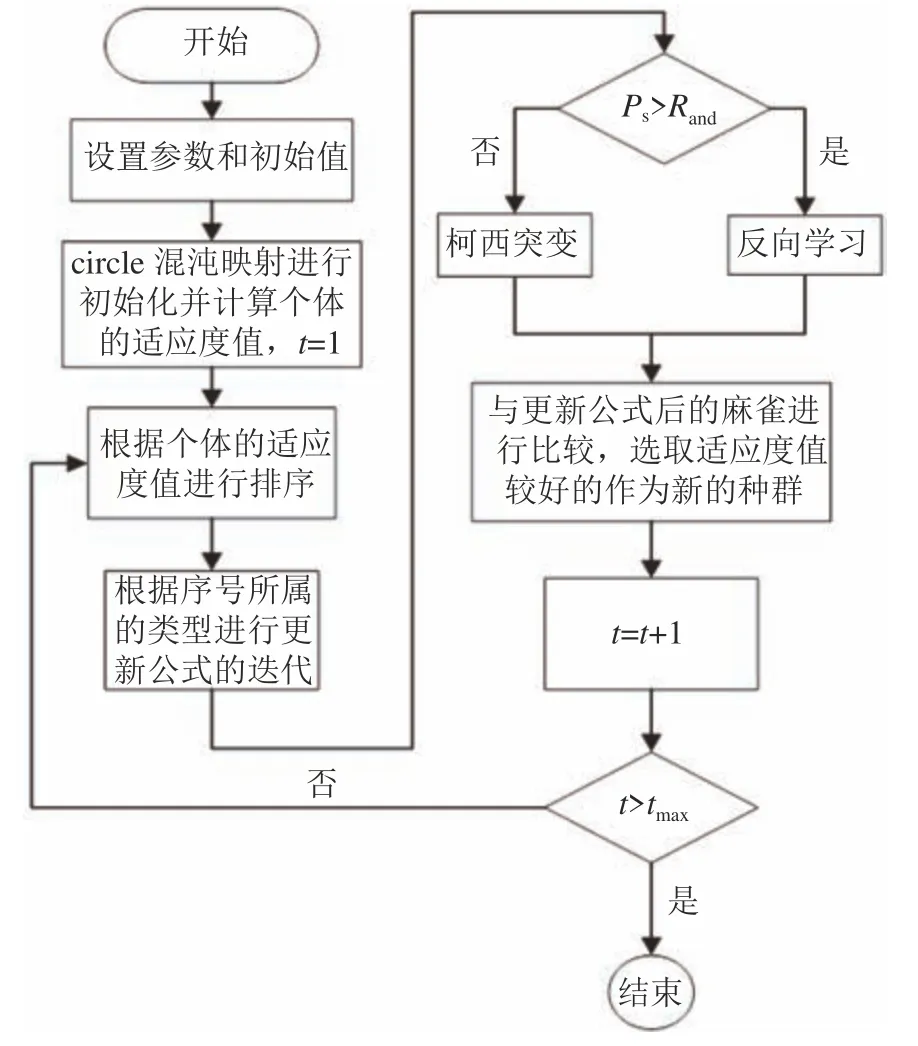
4 仿真与硬件试验
4.1 消融实验

4.2 波浪补偿优化控制
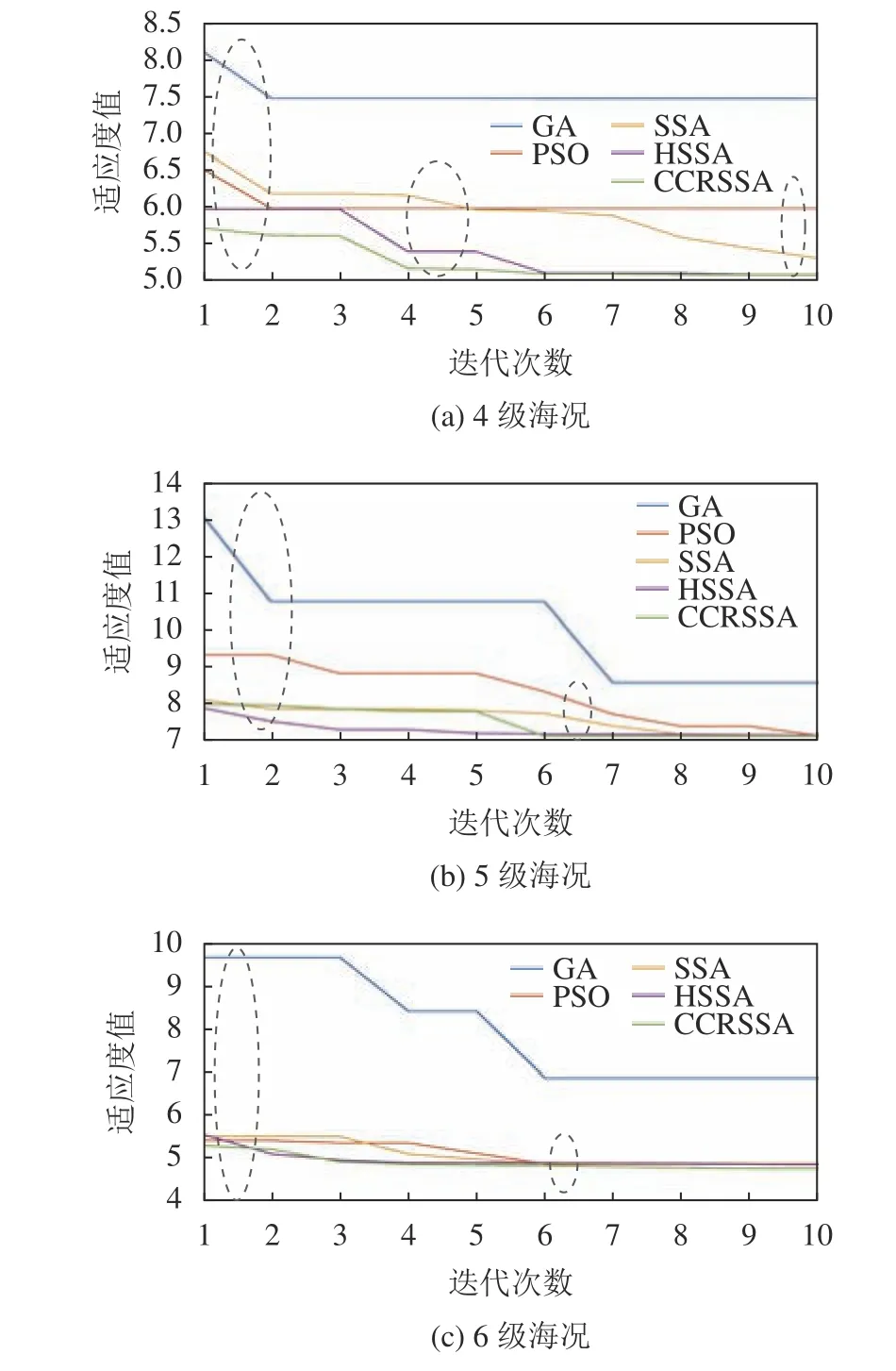

4.3 波浪补偿控制方法对比


4.4 硬件试验



5 结 论

