定制家具板件数控钻孔作业时间预测模型*

欧阳周洲 吴义强 陶 涛 蔡 丰 王 迅 郝绍平

（1. 中南林业科技大学 长沙 410004； 2. 欧派家居集团股份有限公司 广州 510475； 3. 农林生物质绿色加工技术国家地方联合工程研究中心 长沙 410004； 4. 木竹资源高效利用省部共建协同创新中心 长沙 410004）

近年来，随着先进制造技术不断向纵深发展，定制家具制造逐步迈入自动化、连续化阶段。在我国家具制造业转变发展方式、优化经济结构、转换增长动力的关键时期，为满足消费升级背景下的柔性响应（许柏鸣，2023），通过构建家具数字孪生车间（furniture digital twin shop-floor，FDTS）（欧阳周洲等，2022）实现更高效、更低碳的制造，需要依赖更精准的智能生产决策，这就要求需将生产管理由传统的批次级推进到板件级，以削减批次内部粗放式管理造成的效率损失（陶涛等，2022）。工序作业时间是驱动精准生产决策的关键基础数据（陈星艳等，2022），客户个性化需求决定定制家具板件之间的区别，进而导致同一工序加工不同板件时作业时间存在差异。精准生产决策需要围绕每一张板件展开，首先要求掌握板件差异化的工序作业时间（王迅等，2022），在预先实测不具备可行性的现实条件下，产业界对精准预测每一张板件的工序作业时间提出了紧迫要求。

当前，工序作业时间预测相关研究主要集中于构建一套标准模板进行正向计算（Sunet al.，2012）、依据工艺参数进行聚类分析（潘彩霞等，2019）、借助统计学方法构建数学模型（吕闯，2017）、基于人工智能算法和工艺参数进行预测（王孟卓，2020）等方面，研究方法与时俱进，预测精度逐步提高；然而，现有研究大多着眼于定额工时或标准作业时间，不足以指导大规模个性化定制生产模式，同时存在采集数据量过少、对数据基础薄弱的传统制造业适配性不强等问题，且针对家具制造这一特定领域，相关研究相对匮乏（谢艳秋等，2022）。

本研究立足定制家具板件级工序作业时间预测的难题，以核心工序之一——数控钻孔为研究对象，通过MES（manufacturing execution system，制造执行系统）从设备底层和企业数据库采集制造大数据，挖掘关键变量，构建基于定制家具板件特征的数控钻孔作业时间预测模型，并利用真实数据验证模型有效性，探讨不同数据条件下作业时间预测的精度差异，以期解决定制家具板件差异化作业时间数据缺失的现实问题，为定制家具的板件级生产调度夯实数据基础。

1 材料与方法

1.1 试验材料

人造板是大规模定制家具的主要基材，其中刨花板应用最广泛。本研究中数控加工中心加工板件为双面热压三聚氰胺饰面纸并经封边处理的刨花板，基材密度0.69 g·cm−3，含水率6.8%，板件厚度以18 mm 为主，长度、宽度由客户个性化需求结合工艺规则确定，不同板件之间存在较大差异。

数控钻孔加工中心是大规模定制家具板件钻孔的主要装备，借助其柔性制造能力在个性化需求与批量化生产之间寻求平衡（庞国锋等，2019），80%以上板件可通过数控钻孔加工中心一次性加工完成。为满足差异化钻孔作业需求，每一张板件均配备唯一与之对应的参数文件和数控程序。参数文件包含板件上全体孔的位置、直径、深度、进给模式等加工参数，由定制家具拆单软件根据工艺规则在生产前生成；数控程序主要用于指挥加工中心的每一个具体动作，由CAM（computer aided manufacturing，计算机辅助制造）软件根据参数文件结合加工中心的钻头排布、加工范围等设备参数在加工前生成，CAM 软件通常安装在工控机上，专用于生成针对该加工中心的数控程序，也可单独安装并应用于生成针对不同加工中心的数控程序。

定制家具制造使用的典型数控钻孔加工中心及其钻包如图1 所示，每一钻包上通常安装有1 个或多个方向的一组钻头，每一钻头通过气缸实现独立伸缩，相邻钻头中心距32 mm（适配定制家具32 mm 孔位系统），X方向运动的夹具夹持板件与Y方向运动的钻包配合实现在XOY平面上的定位，钻包作Z方向运动进行加工。当板件上某几个孔的位置、直径、深度等参数与钻包上的多个钻头恰好匹配时，几个钻头可同时伸出，一次下钻完成多个孔加工，因此板件上孔的数量与钻包下钻加工次数不完全统一。加工过程中，如果设备靠档、夹具等与钻头、钻包出现干涉，需要额外进行避让。数控钻孔加工中心加工一张板件的流程如图2 所示。

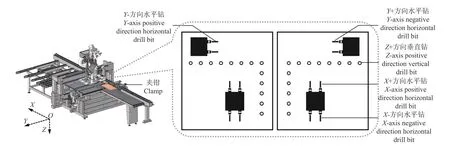
图1 典型数控钻孔加工中心及其钻包Fig. 1 Typical CNC (computer numerical control) drilling machining center and bottom view of its drill bags

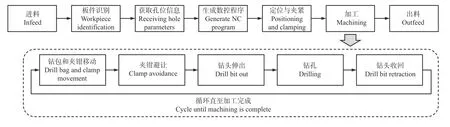
图2 典型数控钻孔加工中心作业流程Fig. 2 Typical operation flow chart of NC drilling machining center

1.2 研究方法

以双饰面刨花板为基材板件，采用数控加工中心进行钻孔作业时，平均作业时间达30 s，是定制家具自动化生产线中时间最长的工序，也常常是瓶颈工序。不同订单的板件尺寸、孔位分布等差异较大，数控钻孔作业时间极差达200 s 以上，且分布不均匀，是引起生产线扰动的主要原因之一。借助调度维持生产线安定，需要精准预测每一张板件的钻孔作业时间，作业时间预测包含数据采集、模型构建和模型评价3 个主要步骤。

1.2.1 数据采集 底层数据缺失是传统制造产业向智能制造产业转型普遍面临的难题。当前，定制家具数控钻孔作业时间预测模型构建所需关键数据大多无直接来源，需要开展广泛的知识挖掘（赵文浩等，2021）。大规模定制家具制造专业化程度较高，为避免频繁调机带来的效率损失和质量问题，通常将基材差异较大的板件分线加工，对于一台数控钻孔加工中心而言板件基材属性波动不大，不同花色饰面纸对数控钻孔作业的影响可忽略不计，进给速度等与基材材质相关的加工参数通常保持恒定；针对常见厚度板件，各类连接件所需的孔通常不需要依据厚度差异化设置，板件厚度对钻孔作业时间的影响可忽略不计；经大量观察与测量，数控钻孔中心加工同一面不同直径的孔时，虽然钻头进给速度不同会带来单次下钻加工时间差异，但相对于整张板件的钻孔作业时间影响较小可忽略不计；钻包和夹具移动距离对作业时间的影响较小，为避免计算复杂度急剧增加带来指数爆炸，该因素暂不纳入考虑。因此，钻孔作业时间主要取决于板件长、宽以及由孔数量决定的下钻加工次数和相关辅助动作次数。

综上，数控钻孔作业时间预测的主要影响因素（模型输入变量）来源于板件工艺特征和设备加工参数（叶正梗等，2019），可通过分析有关工艺规则、参数文件和数控程序，编写解析程序进行提取。针对定制家具企业数据基础良莠不齐的现状，模型输入变量来源与选择总体上可划分为3 种类型：

1） 数据条件较好，排产前借助CAM 软件生成板件在某台加工中心上钻孔的数控程序，可以解析每一张板件对应的数控程序，以设备关键动作为基础构造输入变量；

2） 数据条件一般，CAM 软件无法单独使用，或数控程序存在无法导出、不可读、无法同板件对应等问题，可以解析每一张板件的参数文件，以孔的参数为基础构造输入变量；

3） 数据条件较差，参数文件的提取和解析存在困难，可以从工艺规则着手，通过钻孔规则计算板件孔数作为输入变量。

作业时间预测所需真实加工时间数据通过MES基于加工中心底层的控制逻辑提取。数控钻孔加工中心实际加工过程自夹具夹紧动作开始，至所有夹具松开板件结束（执行避让动作时不允许所有夹具同时松开），可以夹具动力源信号为节点记录时间，并与板件编码绑定，将夹具松开与夹紧之间的时间差作为板件数控钻孔作业时间（即真实值）。

总体数据采集逻辑如图3 所示。

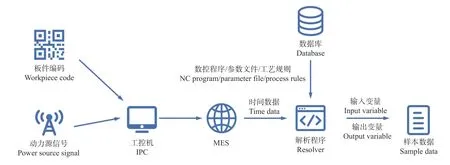
图3 数控钻孔作业时间模型数据采集框架Fig. 3 Data acquisition framework for operation time model of NC drilling

1.2.2 模型构建 数控加工中心作业时间预测的常规思路是逐步计算作业时间并累加，该正向预测方式牵涉到加减速、运动轨迹、触发节点等复杂的设备内部逻辑，资源投入大，运算时间长，应用于定制家具企业存在较大困难，为此，本研究从历史数据着手，通过数据挖掘逆向构建预测模型。线性回归是一种较为简便的逆向建模手段，由于数控钻孔加工的内部逻辑复杂、非线性因素较多，且采集的历史数据存在难以清洗的噪声，线性回归模型预测误差较大，故考虑引入机器学习（于成龙等，2020）方法。人工神经网络（artificial neural network，ANN）对复杂逻辑具备很强的自适应能力，可以良好描述非线性关系，其分布式处理模式具有较强的鲁棒性和容错性，对异常值较为健壮，且已在其他类似领域回归预测中得到成熟应用（刘子文等，2021），故本研究主要探讨采用人工神经网络方法构建定制家具板件数控钻孔作业时间预测模型。

人工神经网络由M-P 神经元（McCullochet al.，1943）组成，单个神经元以一定权重接受多个输入，经激活函数f处理输出y，其数学表达式（周志华，2016）如下：

式中：xk为输入变量；i为输入变量个数；wk为每个输入变量对应的权重；θ 为阈值。

单个神经元仅包含输入层和输出层，只能处理简单的线性回归问题，对于复杂的数控钻孔作业时间模型，需在输入层与输出层之间添加隐层。人工神经网络只需要一个神经元数量足够多的隐层即可任意精度逼近任意复杂度的连续函数（Horniket al.，1989），为此构建一个由单隐层组成的3 层神经网络，见图4。

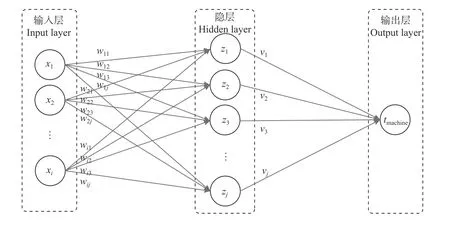
图4 数控钻孔作业时间的3 层神经网络模型Fig. 4 Three layer neural network model of NC drilling operation time

将式（1）延伸到3 层神经网络，其隐层神经元输出可表达为：

模型输出可表达为：

激活函数使用针对回归模型效果较好的Mish 函数（Misra，2019），其表达式为：

目前尚无完善的理论支撑隐层神经元数量的精确计算，多数情况下只能通过经验公式与反复测试相结合的方式获得。为了避免隐层神经元过少造成学习能力下降或神经元过多造成过拟合现象，考虑到样本数据量足够大的基本情况，可在Jadid 等（1994）给出公式的基础上进行试凑，其公式如下：

式中：j为隐层神经元数量；n为训练集样本数量；i为输入变量个数；l为输出结果个数，在数控钻孔作业时间预测模型中，l=1。

人工神经网络训练的基本思路是利用包含n条数据的大数据集不断调整式（2）与式（3）中wkm、vm、θ1m、θ2等参数的组合，使模型预测值tpred与真实值ttrue最接近，通过损失函数最小化进行评价。由于预测结果y∈(0,+∞)，且集中度较低，不适宜应用误差百分比衡量，且存在因产线拥堵造成作业时间数据偏大的异常现象，故本研究选用对异常值比较健壮的平均绝对误差（mean absolute error，MAE）作为损失函数，其计算公式为：

为提高模型收敛速度和精度，消除量纲影响，需对数据进行缩放，同时为应对可能存在的异常值，采用标准化方法进行处理，其计算公式为：

式中：xstd为标准化处理后的变量；x为原始变量；μ、σ 分别为变量的均值和标准差。

误差逆传播（error back-propagation，BP）是求解人工神经网络各参数值的经典算法，采用梯度下降策略更新参数。对于大数据集，小批量梯度下降法（mini-batch gradient descent，MBGD）可有效避免陷入局部最优解和运算量过大的局面。考虑计到算机的并行运算能力以及较大的样本量，本模型训练批量选用512。

为规避局部最优解和鞍点，同时提升模型训练效率，在BP 算法权重更新方程的基础上增加一个动量（momentum），以实现权重更新的平滑。新的权重更新公式（史忠植，2016）为：

式中：wp为第p行的权重；β 为动量参数，本模型中β=0.9；η 为学习率；E为依据损失函数计算的误差。

在权重更新过程中，采用线性衰减算法实现学习率η 的自调节，以加快收敛速度并避免震荡。对于第q次迭代，其学习率计算方法为：

式中：η0为初始学习率，本模型中取0.01；α 为衰减率，α 越大学习率衰减越快，需经不断测试得到一个较优的取值。

通过添加一个早停策略，能够有效避免模型过拟合，即当验证集损失函数在一定次数内不再下降时，停止训练并输出训练完成的模型，初步设置该参数为500 次。

训练完成后将测试集输入变量以相同的标准化方法输入模型，输出结果经逆标准化处理，可得到测试集预测值。

1.2.3 模型评价 模型预测精度评价依托测试集样本数据，使用基于不同数据条件和对应超参数组合训练的模型分别对测试集各样本进行预测。为验证基于3 层神经网络模型的预测精度，分别将基于对应数据条件建立的线性回归模型预测结果作为对照。

对于预测结果，通过不同模型预测值的极大值、极小值、极差、平均值和标准差5 个指标与真实值的接近程度进行评价。对于模型精度，选用对异常值比较健壮的平均绝对误差（MAE）（式6）和决定系数（R2）（式10）作为直接评价指标（侯志康等，2022），并通过预测值与真实值回归关系（付宗营等，2020）、预测绝对误差占比进行可视化呈现：

式中：ttrue为真实时间；tpred为预测时间；t为平均作业时间；n为样本量。

上述指标中，MAE 越小，预测精度越高；R2越接近1、预测值与真实值回归直线与直线y=x夹角越小，预测值与真实值之间偏差越小；绝对误差占比中，误差较小的占比越大，预测效果越好。

2 结果与分析

在欧派家居集团股份有限公司开展实践研究，基于上述框架采集其某柜身生产线SKD-6125 通过式六面数控钻孔加工中心60 个工作日加工的柜身板件（主要包含顶板、底板、层板、侧板等）历史数据63 481 条，并同步获得对应的数控程序、参数文件和工艺规则。考虑到无孔板件作业时间恒为0，将其去除以避免对模型的干扰，并对明显异常数据进行清洗，实际得到样本60 443 条。以天为单位近似按照8∶1∶1 划分，得到训练集48 180 条、验证集6 583 条、测试集5 680 条。

2.1 变量组合及其相关性

基于不同数据条件获得的输入变量组合如表1所示。

表1 不同数据条件下数控钻孔加工中心输入变量①Tab. 1 Input variables of NC drilling machining center under different data conditions

对采集的全体样本进行多元回归分析，分别计算不同数据条件下调整后的R2（表2）。随着数据条件不断提高，可获取的变量数量增多，调整后的R2不断升高，即所取变量对数控钻孔作业时间的可解释性不断增强，对预测精度提高具有显著意义。

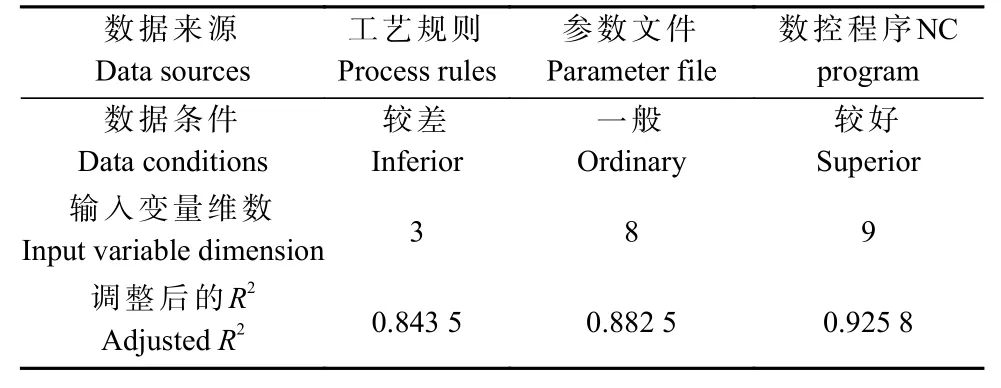
表2 不同数据条件下输入变量与作业时间的相关性Tab. 2 Correlation between input variables and operation time under different data conditions

2.2 预测结果分析

真实数据、不同数据条件下构建的数控钻孔作业时间模型及对照线性回归模型预测结果总体情况如表3 所示。

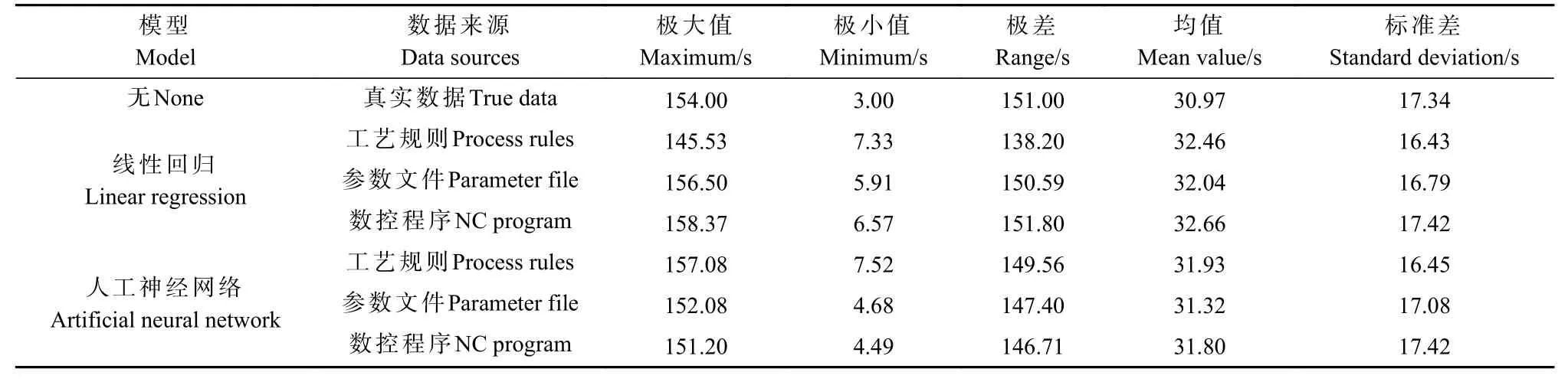
表3 不同模型预测结果总体情况Tab. 3 General situation of prediction results of different models

由表3 可知，人工神经网络模型预测结果的分布指标优于其他模型，对平均作业时间的预测误差为0.83 s，误差率为2.68%，具备对工序总体效能进行预测的能力；线性回归模型普遍存在预测值偏大的情况，其主要原因是模型对异常值较敏感，因拥堵造成作业时间偏大的样本对预测结果产生整体偏移；对基于数控程序提取的9 维变量进行线性回归，在极差和标准差方面同实际数据比较接近，该情况本质上是由于这9 个变量同设备实际作业时间的构成逻辑基本一致，是传统建模手段能够构建的最精准的预测模型。

2.3 模型精度分析

将当前产业界使用的平均作业时间纳入对照，分别计算不同数据条件下数控钻孔作业时间模型以及其他对照模型的MAE 与R2（表4），并绘制评价图（图5、图6）。

表4 不同数据条件各模型预测精度对比Tab. 4 Comparison of prediction accuracy of various models from different data sources

图5 真实值与预测值回归关系对比Fig. 5 Comparison of regression relationship between true value and predicted value

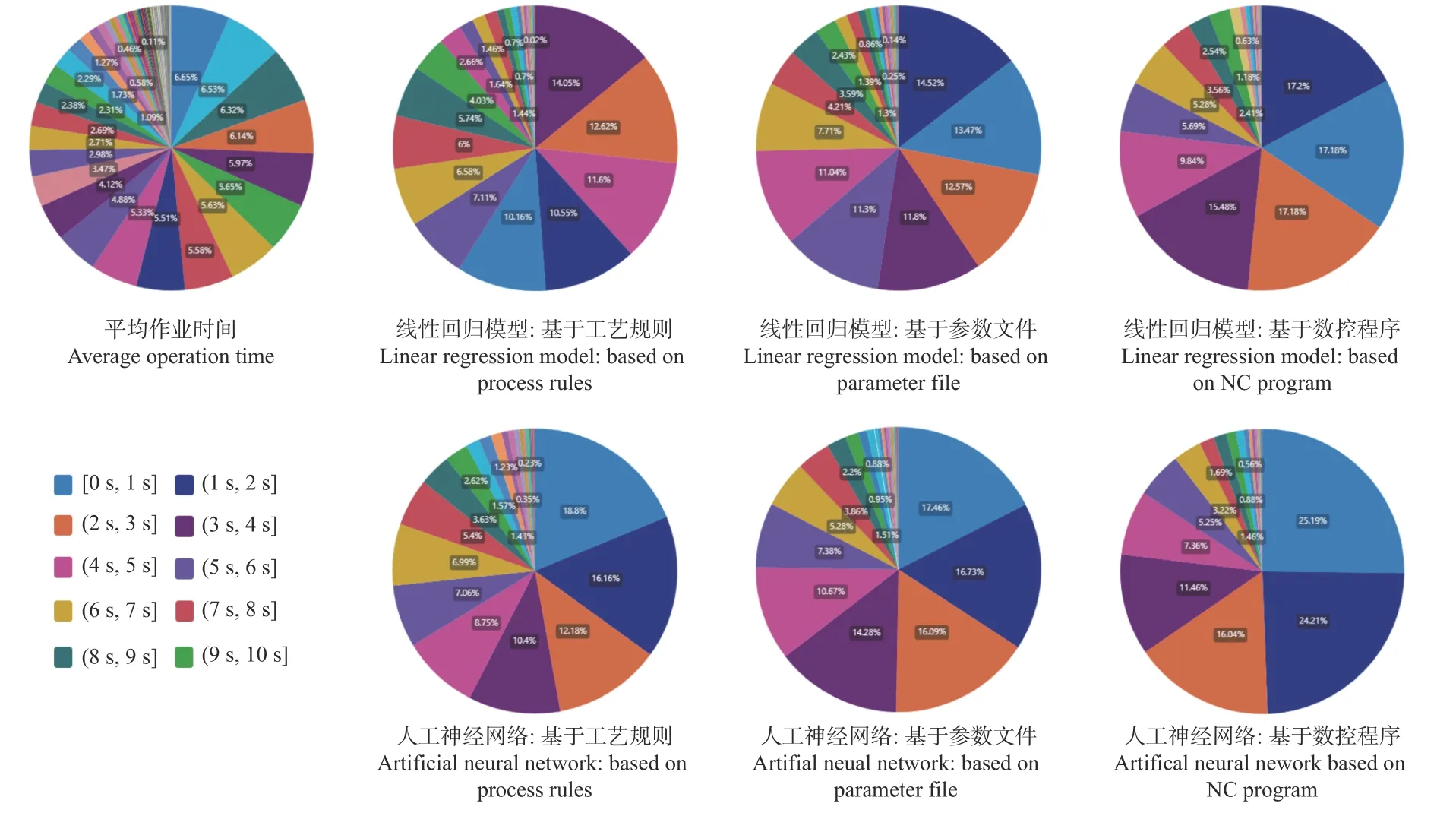
图6 预测绝对误差占比对比Fig. 6 Comparison of prediction absolute error percentage

从不同数据条件的维度来看，本研究提出的基于人工神经网络建模预测结果MAE 分别为4.32、3.76 和2.87 s，相比采用当前使用的平均作业时间，3种数据条件下预测的MAE 分别缩减62.95%、67.75%和75.39%；3 种数据条件预测值对实际值的可解释比例均达88%以上，具有较高预测精度；随着数据条件优化，预测值与真实值回归直线与直线y=x的夹角不断减小，印证了基于数控程序提取的输入变量采用本研究构建模型预测的效果；绝对误差占比中，预测绝对误差较小的样本占比显著增加，绝对误差1 s 内的板件达25.19%、3 s 内的板件达65.44%，前80%板件最大绝对误差不足5 s。数据来源从工艺规则逐步深入到参数文件和数控程序，本质上是一个正向推进过程，除可取得的变量维数增多外，更重要的是加工过程确定性逐步增加，使得预测结果逐步精确。

从不同预测方法的维度来看，本研究构建模型基于3 种数据条件预测的MAE 相比常规线性回归分别缩减18.80%、17.72%和20.28%；预测值对真实值的可解释比例分别提升4.10%、3.46%和1.32%；预测值与真实值回归关系的样本分布和绝对误差占比中低误差样本占比同样佐证上述结果，不同数据条件下预测误差1 s 内的板件占比分别提升85.04%、29.62%和46.62%，3 s 内的板件占比分别提高13.82%、9.72%和13.87%，前80%板件预测绝对误差相比线性回归预测结果缩短2、1 和1 s，相比采用平均值缩短56.25%、62.50%和68.75%，表明本研究构建的模型预测精度在各种数据条件下优于传统线性回归方法。

3 结论

本研究立足定制家具制造实际、面向家具智能制造需求，基于人工神经网络构建模型实现了数控钻孔工序作业时间的预测，并将预测粒度推进到板件级，预测均值误差0.83 s，平均绝对误差2.87 s；论证了不同数据条件下均具备良好预测性能，且显著优于同条件下常规线性回归预测，初步具备指导定制家具精准生产决策的能力。未来可在消除数据采集误差、优化算法性能和提高预测精度方面展开更深入研究。本研究提出的相关方法还可拓展到其他工序，对于家具产业复杂数控工序的板件级作业时间预测以及精准生产决策具有一定借鉴意义。