基于A-CGAN的深反射地震数据随机噪声压制方法研究
韩建光,王卿,许媛,刘志伟
1)中国地质科学院,北京,100037;2)北京信息科技大学,北京,100101
内容提要:基于深度学习的地震数据噪声压制方法是当前地震数据去噪处理的重要方向。深度学习方法突破了传统滤波处理的局限,在对常规地震数据的噪声压制中表现出效率高、信噪分离效果好的特点。但针对深部弱有效反射数据,当前的深度学习方法特征提取能力有限,难以取得较好的去噪效果。笔者等结合深反射地震数据特点,针对当前深度学习噪声压制方法在特征提取及对数据集依赖上的局限,提出了基于注意力循环生成对抗网络(Attention Cycle-Consistent Generative Adversarial Networks,A-CGAN)的深反射地震数据随机噪声压制方法。借助循环一致生成对抗网络(Cycle-Consistent Generative Adversarial Networks,Cycle-GAN)的域映射思想,降低对数据集的要求。为了构建适用于深反射地震数据的去噪网络,从3个方面对Cycle-GAN进行改进:在Cycle-GAN的生成器(去噪器)中加入残差结构和注意力机制,用于加深网络深度和提高其特征提取能力;在Cycle-GAN的鉴别器中使用块判决,提高鉴别精度和准确度;在损失函数部分加入感知一致性损失函数,提升网络模型恢复纹理细节信息的能力。通过合成地震数据和实际深反射地震数据测试,验证了优化算法的有效性,体现了良好的应用价值。
深反射地震数据精细处理是深反射地震探测取得成功的关键(王文光等,2021;谭晓淼等,2021)。对于深反射地震深层数据,探测目的层深度大,数据观测接收排列长度跨度广,观测方法的特殊性和探测区域地质条件的复杂性,造成深层有效反射信号弱,受噪声干扰严重,成像效果差,制约对深部构造形态的认识。因此研究有效的噪声压制方法,最大限度地去除噪声,保护有效信号,提升资料信噪比,实现深层微弱反射信号的清晰成像,对深部地震勘探至关重要。深反射地震数据传统的噪声压制方法主要包括异常振幅噪声衰减、局部异常振幅衰减、径向预测滤波噪音衰减、相干噪音衰减、地震子波反褶积处理、随机噪音衰减等(朱小三等,2013;徐泰然等,2017;谷丙洛等,2020;杨顺等,2023)。这些方法都有其自身适用的范围,在对深反射地震数据处理过程中需要根据噪声具体特征,利用不同域中有效信号的特点及其与其他信号之间的差异,合理且有针对性地选择和应用去噪方法,对处理人员要求高并且处理效率较低。面对深部低频随机噪声与低频有效信号严重重叠的情况,传统去噪方法通常难以取得较好的去噪效果(邢涛等,2023)。
近年来,随着计算机硬件的飞速发展,深度学习在图像去噪领域取得了巨大的成功(Vasudevan and Jesse, 2019; Tian Chunwei et al., 2020; Xia Haiying et al., 2020)。深度学习方法具有自主学习、快速提取特征、精准拟合复杂非线性映射等优点。深反射地震数据中的有效信号具有较强的纹理特征,可以被视为一种更加复杂的含噪图像,因此可以使用深度学习方法智能化完成噪声压制和有效信号恢复的任务,相较于传统方法,深度学习方法对数据处理经验依赖程度低,对深反射地震数据处理更加智能和高效。研究深反射地震数据随机噪声的智能压制方法,对于地震深部探测具有重要的理论意义和应用价值。
基于卷积神经网络(Convolutional Neural Networks,CNN)的方法在噪声压制方面效果最好,取得了优于传统方法的新突破。罗仁泽等(2020)提出了一种U型卷积神经网络用于地震资料随机噪声压制,通过对叠后地震数据处理并与传统小波等去噪方法比较,证明了深度学习方法的高效性及可行性;Jin Yuchen等(2018)和Wang Feng等(2019)使用合成数据验证了卷积神经网络的去噪性能;韩卫雪等(2018)、李海山等(2020)、Yang Liuqing等(2020)将残差卷积用于地震数据去噪,通过模拟数据测试和实际资料应用证明了深度学习方法的有效性;Zhao Yuxing等(2019)和Dong Xintong等(2020)针对沙漠地震数据受低频噪声干扰严重的问题,说明了传统去噪方法的局限,并将卷积神经网络用于沙漠地震数据去噪,证明了卷积神经网络在沙漠地震数据去噪领域的巨大潜力。上述研究验证了深度学习网络在地震数据噪声压制领域的可行性。然而,在深反射地震去噪处理领域,基于人工智能去噪方法的研究和应用还处于起步阶段,如何利用人工智能方法对弱有效信号、强噪声干扰的深反射地震数据进行随机噪声的压制是亟需解决的技术难题。此外,CNN方法均基于监督学习,需要构建大量含标签的成对数据,而实际地震数据虽然体量大,但由于复杂噪声的干扰无法获得用作标签的干净数据,若使用其他方法的去噪结果作为标签,最终的去噪效果能否超出标签效果令人怀疑,同时基于CNN去噪方法的优化过程通常是最小化去噪数据与理论纯净数据之间的均方误差(Mean Square Error,MSE),而MSE衡量结构完整性的能力非常有限,缺乏对数据分布尤其是结构特征的描述(Zhang kai et al., 2017)。
为了克服CNN去噪的不足和局限,生成对抗网络(Generative Adversarial Networks,GAN)开始被研究和应用。Alwon(2018)通过构建适当的生成器和判别器,对生成对抗网络在地震数据处理方面的可行性进行了初步研究。Wang Hongzhou等(2021)、Ma Haitao等(2022)将属性编码与GAN结合用于沙漠地震数据噪声压制,通过引入新的损失来约束有效反射的恢复和地震噪声的衰减。然而,当前基于GAN的去噪方法研究主要针对浅部强反射信号数据,针对深反射弱地震数据的去噪方法还处于空白。
针对这些问题,笔者等通过改进网络结构和损失函数,提升对深反射地震数据随机噪声的压制效果。以循环一致成对抗网络(Cycle-GAN)为基础,提出一种基于注意力循环生成对抗网络的深反射地震数据随机噪声压制方法(Attention Cycle-Consistent Generative Adversarial Networks, A-CGAN)。针对数据集要求高的问题,A-CGAN借助Cycle-GAN的域映射思想,无需成对数据即可自动训练网络,完成从含噪域地震数据到无噪域地震数据的映射,实现以无监督形式训练网络。为了进一步加强网络的去噪精度,通过加入感知一致性损失函数,提升去噪数据的恢复精度和细节信息,合成地震数据和实际数据测试验证了该方法的有效性。
1 A-CGAN网络结构和去噪原理
生成对抗网络(GAN)是受博弈论中零和博弈思想启发构建的一种网络,它由生成器和鉴别器两部分组成(Ledig et al., 2016)。其中,生成器的目标是尽可能地生成可以骗过鉴别器的“真实”数据,而鉴别器的目标是最大限度地鉴别出接收到的数据是真实数据还是生成器生成的结果,二者相互对抗直至达到纳什平衡。原始生成对抗网络用于去噪任务时仍然需要构建成对数据,无法满足降低数据集要求这一目标,基于注意力循环生成对抗网络的深反射地震数据随机噪声压制方法(A-CGAN),借助Cycle-GAN的域转换思想,在非成对数据集上训练出有效的去噪网络。
1.1 A-CGAN网络结构
图1所示为A-CGAN的网络结构图,其中Gx→y和Gy→x表示注意力生成器(去噪器),Dx和Dy表示鉴别器。从整体结构图中可以看出,整个网络训练成熟之后,使含噪数据映射为无噪数据的Gy→x即为所需的注意力去噪器。A-CGAN包括两个部分,其中y→y′部分中,首先将纯净地震数据送入鉴别器Dx,让鉴别器学习纯净地震数据的概率分布,然后将模拟合成的含噪地震数据y输入去噪器Gy→x中,去噪器经过处理后得到去噪后的深反射地震数据x′,接着将得到的去噪结果送入鉴别器Dx,判定真伪,最后为了防止y域中的所有数据均映射为x域中的同一数据,使用循环一致性损失和感知一致性损失进行约束,至此完成了从含噪域(y域)至纯净域(x域)的映射;x→x′部分与y→y′同理,首先将含噪地震数据送入鉴别器Dy,让鉴别器学习含噪地震数据的概率分布,然后使用Dy对生成的含噪地震数据y′进行鉴别,最后为保证数据一致性,使用循环一致性损失和感知一致性损失进行约束。在去噪器和鉴别器的对抗过程中,去噪器和鉴别器的能力均不断增强,当鉴别器训练至无法鉴别数据输入并且整个网络达到动态平衡时,此时的注意力去噪器即为所需的去噪网络。
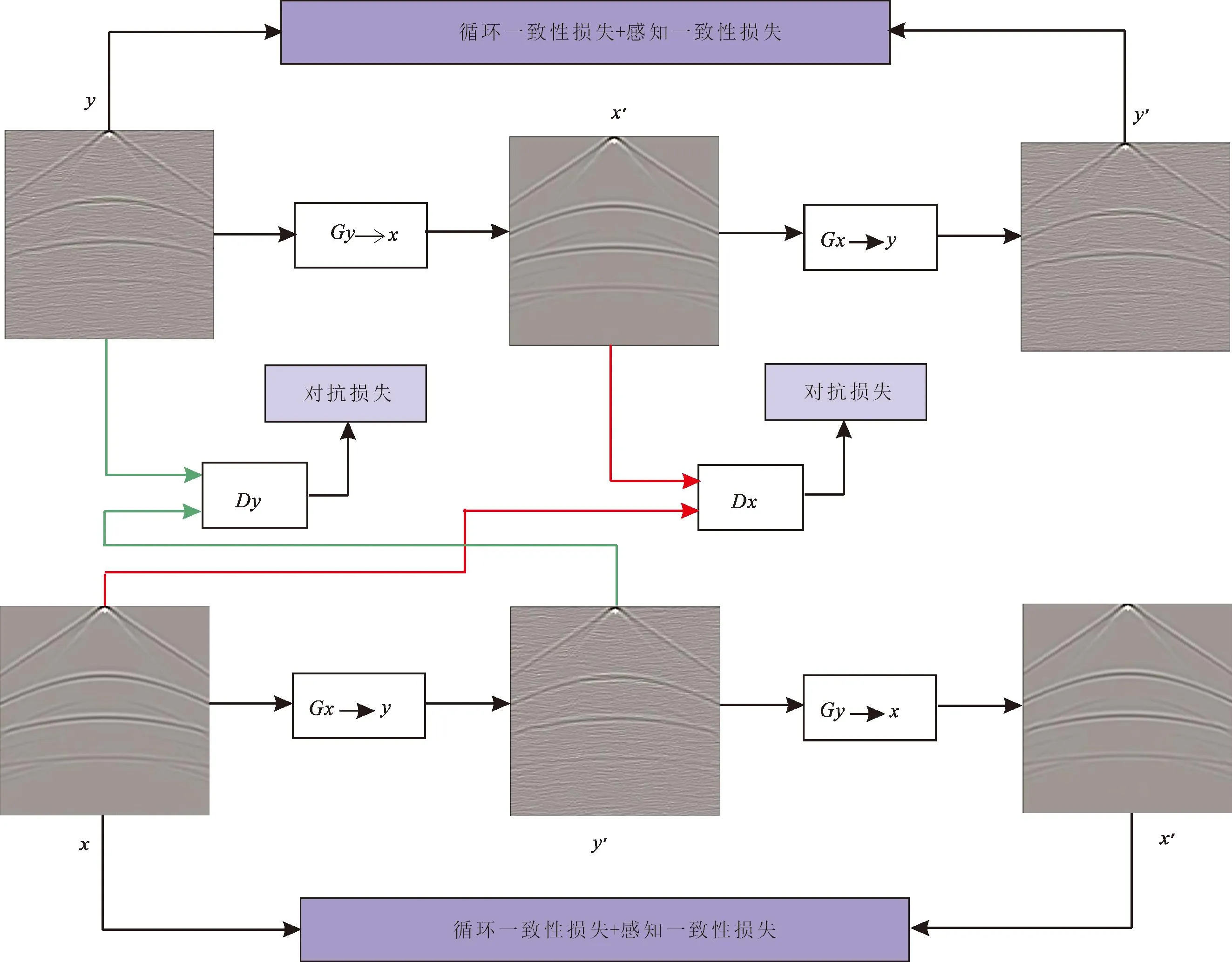
图1 A-CGAN网络结构图Fig.1 A-CGAN network structure diagram
A-CGAN的注意力去噪器是一个结合了注意力机制和Res-Net的神经网络。Res-Net可以通过网络训练建立复杂的映射关系,有效解决随网络深度增加网络退化的问题。注意力机制可以辅助网络捕捉关键信息,提高特征提取能力,更好地恢复深反射地震数据中的微弱有效信号。图2为注意力去噪器的网络结构,使用64个3×3卷积核对输入数据进行特征提取,经过批标准化(BN)、ReLu激活函数、下采样,进入由9个残差块组成的Res-Net网络,通过注意力机制SENet提升关键特征权重后经过上采样,之后仍采用3×3的卷积核进行卷积处理,最后经过Tanh激活函数,输出与输入数据尺寸相同的数据。
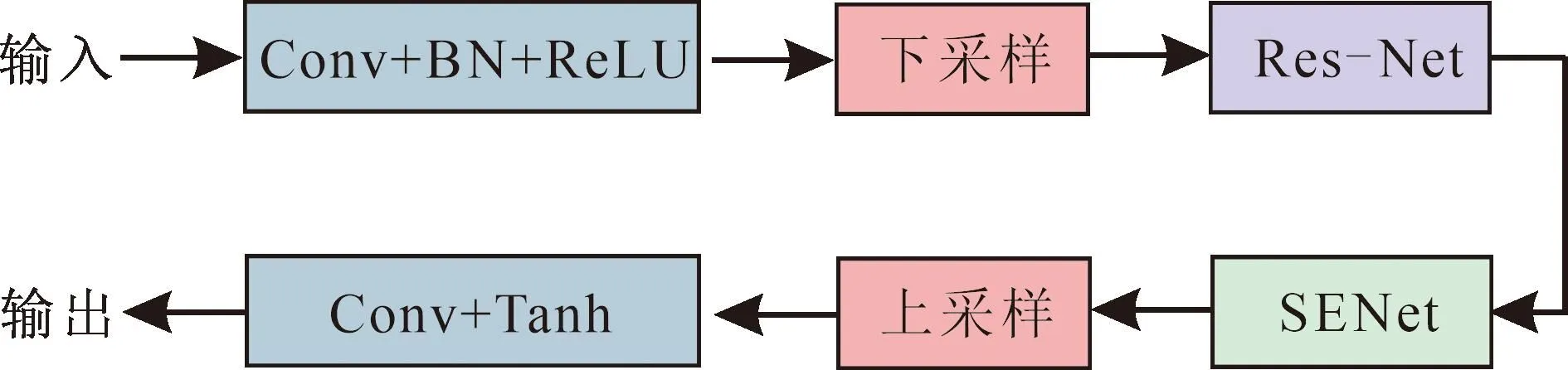
图2 A-CGAN注意力去噪器结构图Fig.2 Structure diagram of A-CGAN attention noise eliminator
普通GAN的鉴别器最后的鉴别输出通常为一个标量,该数值是数据整体的加权值无法体现出数据局部特征,对于精度要求高的任务效果不佳。A-CGAN使用块判别的思想,使得输出结果为一个矩阵,矩阵中的每一个元素代表输入数据某一部分的鉴别结果,因此具有更高的分辨率和准确性。图3为使用块判决思想的A-CGAN鉴别器结构图。使用不同层深,卷积核大小均为3×3的卷积层对输入数据进行处理,每次卷积处理后都需要经过批标准化(BN)、ReLu激活函数处理,最终输出32×32的矩阵,该矩阵的每个元素值代表输入数据某部分为真实数据的概率。
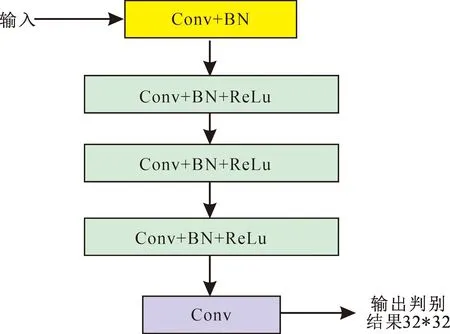
图3 A-CGAN鉴别器结构图Fig.3 A-CGAN discriminator structure diagram
1.2 A-CGAN去噪原理
含噪深反射地震数据y可以表示为:
y=x+n
(1)
其中,x表示纯净地震数据,n表示深反射噪声数据。A-CGAN通过损失函数约束训练过程,引导训练逐步向期待的方向进行。与原始Cycle-GAN不同的是A-CGAN的损失函数由循环一致性损失、感知一致性损失、对抗损失三部分构成。下面分别介绍三部分损失对整个网络训练的作用。
(1) 循环一致性损失。该损失是Cycle-GAN中原有的,它使用L1正则化计算原始输入与循环生成输出之间的逐像素平均误差,结合A-CGAN结构图,其表示为:
Lcycle(Gx→y,Gy→x)=
(2)
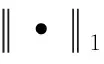
(2) 感知一致性损失。为了更好地恢复纹理细节信息,使用感知一致性损失改善生成数据的质量。该损失可以让网络关注更加抽象的高层次信息,从而在重建过程中更加真实。感知一致性损失函数采用Johnson等人的思想(Johnson et al., 2016),将原始数据和循环生成的数据经过预训练好的VGG-16网络,然后提取经过该网络5层池化层的特征图。感知一致性损失定义为:
Lperceptual(Gx→y,Gy→x)=
(3)
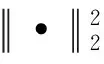
(3) 对抗损失。对抗损失通过竞争的方式训练注意力去噪器和鉴别器,使得双方在对抗过程中去噪器产生更接近源域的数据。原始Cycle-GAN的对抗损失使用交叉熵损失约束对抗过程,这可能会导致梯度消失(Yeung et al., 2022)。因此为了更好训练鉴别器,A-CGAN使用最小二乘损失替换交叉熵损失,用于解决训练过程中梯度消失的问题。其定义如下:
Ladversarial(Gx→y,Gy→x,Dx,Dy)=
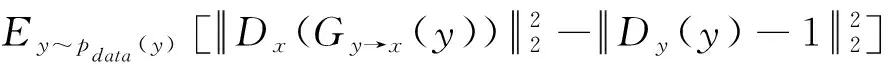
(4)
最后,A-CGAN的总体损失函数可以表示为:
Ltotal(Gx→y,Gy→x,Dx,Dy)=λ×Lcycle(Gx→y,Gy→x)
+β×Lperceptual(Gx→y,Gy→x)+
Ladversarial(Gx→y,Gy→x,Dx,Dy)
(5)
整个模型的总体优化目标可以表示为:
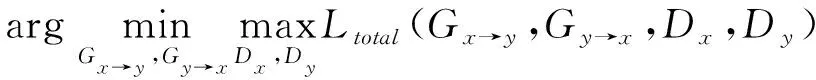
(6)
上式表征一个最大最小优化问题,arg min max表示最大最小目标函数,优化终止于相对于去噪器的最小值和相对于鉴别器的最大值的鞍点。利用总损失函数模型不断约束优化,使得去噪器生成的地震数据最终不断趋近真实无噪音数据。当整个网络模型达到动态平衡,损失函数下降并逐渐趋于稳定后,此时的Gy→x即为所需的去噪器。A-CGAN的训练不需要构建一一对应的成对数据集,只需要纯净地震数据(图4a)和含噪地震数据(图4b)两个域的数据即进行网络训练。合成含噪地震数据与纯净地震数据构建数据集时打乱二者顺序,不需要一一对应,故可以在含噪地震数据中加入实际深反射含噪数据。模型训练仍采用数据块的形式,块大小同样为50×50。

图4 部分非配对地震数据训练集:(a)纯净地震数据块;(b)含噪地震数据块Fig.4 Partial unpaired seismic data training set: (a) pure seismic data block; (b) noisy seismic data block
2 实验测试与分析
2.1 合成地震数据处理结果分析与对比
利用有限差分正演模拟方法(朱广辉等,2020)合成纯净的地震数据,并将其与未参与训练的噪声数据叠加合成含噪地震数据,用于注意力去噪网络测试。图5a为采用雷克子波合成的纯净地震数据,图5b为真实深反射地震随机噪声,图5c为叠加真实地震噪声后的含噪地震数据,该含噪地震数据的信噪比为-10.147dB,RMSE为1.384。

图5 合成地震数据: (a)纯净地震数据;(b)噪声地震数据;(c)合成含噪地震数据Fig.5 Synthetic seismic data: (a) pure seismic data; (b) noisy seismic data; (c) synthesis of noisy seismic data
使用A-CGAN中的注意力去噪器、Cycle-GAN去噪模块、小波变换、带通滤波器分别处理图5c中的合成含噪地震数据,4种方法的去噪结果如图6a—d所示。从图中可以看出,A-CGAN可以有效压制噪声且较好地恢复了有效信号的同相轴,Cycle-GAN虽然可以在一定程度上压制噪声,但是有效信号同相轴清晰度较差,处理效果不如本文改进的方法。与深度学习方法相反,传统方法的去噪结果中仍然存在大量的噪声,有效信号同相轴仍然淹没在噪声中。其中,小波变换的去噪结果(图6c)中虽然可以看出有效信号的基本走向但是仍残留有较多的背景噪声,带通滤波器的去噪结果 (图6d)中,处理效果较差甚至出现虚假地震反射(如图中黄框部分)。
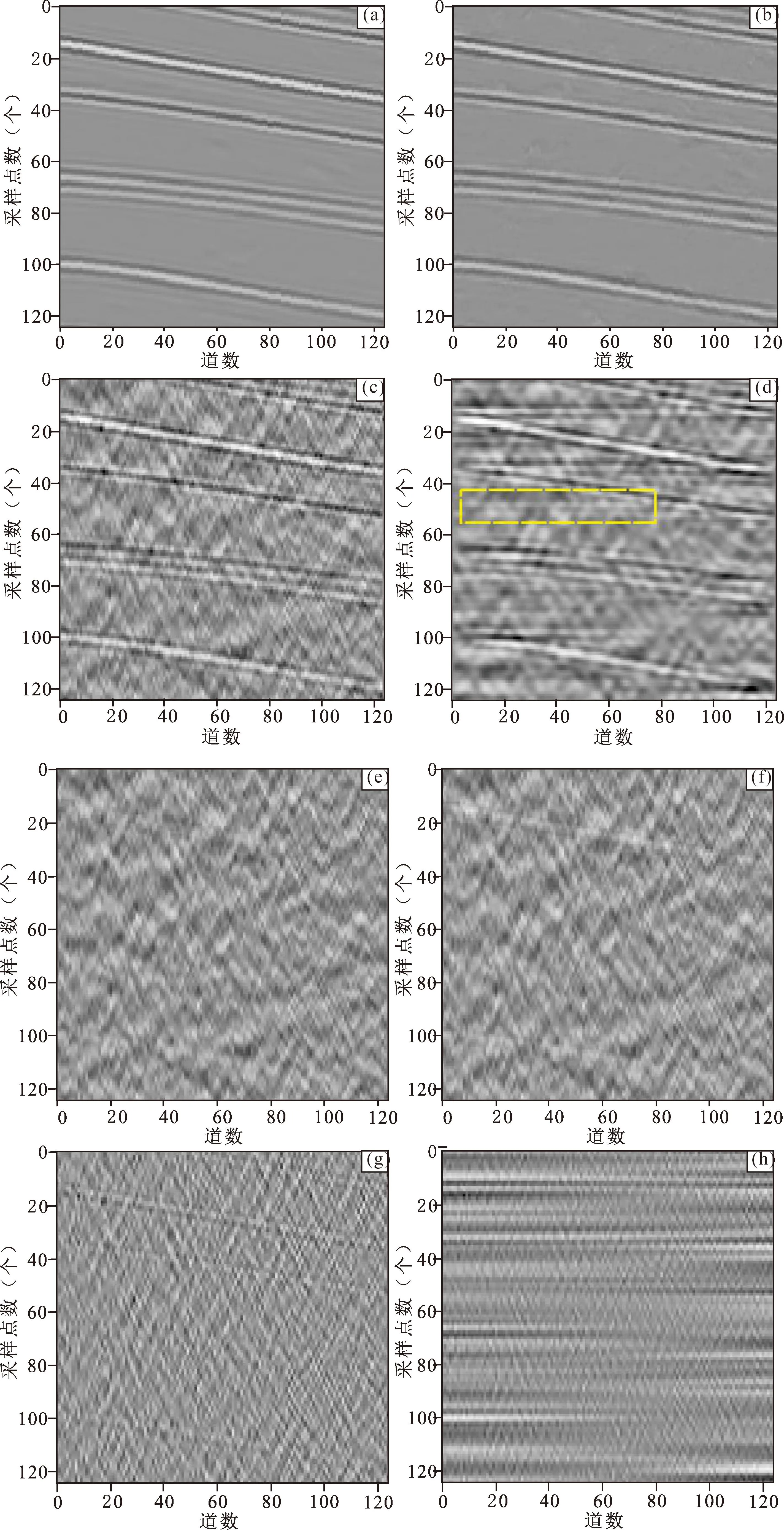
图6 合成地震数据去噪结果对比 与去噪结果残差图:(a) A-CGAN去噪结果;(b) Cycle-GAN去噪结果;(c) 小波去噪结果;(d) 带通滤波器去噪结果;(e) A-CGAN去噪残差;(f) Cycle-GAN去噪残差;(g) 小波去噪残差;(h) 带通滤波器去噪残差Fig.6 Comparison of denoising results of synthetic seismic data and residual diagram of denoising results: (a) A-CGAN denoising results; (b) Cycle-GAN denoising results; (c) wavelet denoising results; (d) denoising result of bandpass filter; (e) A-CGAN denoising residual; (f) Cycle-GAN denoising residual; (g) wavelet denoising residuals; (h) band pass filter denoising residual
下面给出4种去噪结果的残差图,用于对比4种方法对有效信号的保护能力(图6e—g),可以看出A-CGAN对应的残差图最接近纯噪声数据,其余3种方法的残差图中都不同程度地带有有效信号同相轴,说明Cycle-GAN、小波变换、带通滤波器3种方法在压制深反射地震噪声的同时也滤除了部分有效信号。
2.2 频域分析
图7a—f显示了纯净地震数据、含噪地震数据和四种方法去噪结果的F—K谱图。从图7a和图7b中可以看到,有效信号和深反射地震噪声在0~30 Hz之间混叠严重。从图7c—f中可以看到,A-CGAN的去噪结果F—K谱图最接近纯净地震数据F—K的谱图,说明本文提出的深反射地震数据去噪网络可以在共享频带里实现有效信号和深反射地震噪声的有效分离,进而压制深反射地震随机噪声并恢复弱有效信号的结构。图7d中可以看出Cycle-GAN可以压制多数随机噪声,但是在频谱混叠严重的部分信噪分离能力不足(如红框部分)。传统压制方法小波变换(图7e)和带通滤波(图7f)的F—K谱图中包含大量随机噪声成分,且共享频带的有效信号和随机噪声没有实现有效分离。综上所述,传统方法无法在噪声压制和有效信号恢复之间达到好的平衡,而未改进的Cycle-GAN由于特征提取能力有限,共享频带信噪分离能力较弱。
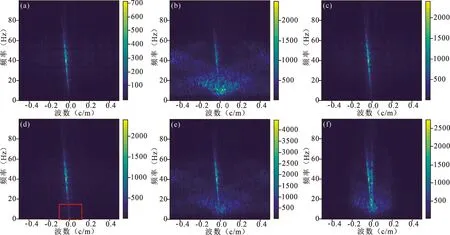
图7 去噪结果F—K谱图:(a) 纯净地震数据F—K谱图;(b) 含噪地震数据F—K谱图;(c) A-CGAN去噪结果F—K谱图;(d) Cycle-GAN去噪结果F—K谱图;(e) 小波变换残差数据F—K谱图;(f) 带通滤波器残差数据F—K谱图Fig.7 F—K spectra of denoising results: (a) F—K spectra of pure seismic data; (b) F—K spectra of noisy seismic data; (c) F—K spectra of A-CGAN denoising results; (d) F—K spectra of Cycle-GAN denoising results; (e) wavelet transform residual data F—K spectrum; (f) F—K spectrum of band-pass filter residual data
下面对纯噪声地震数据和残差噪声数据进行频域分析。图8a—e中展示了纯净噪声数据和4种去噪残差的F—K谱图。从图中可以看到A-CGAN的残差F—K谱图与纯噪声地震数据的F—K谱图最为接近,仅有很少的有效信号残留,说明A-CGAN在压制随机噪声的同时对有效信号的能量衰减影响最小,能够有效保护有效信号幅度。Cycle-GAN、小波变换、带通滤波的残差F—K谱图中均不同程度的存在有效信号能量残留,尤其是传统方法小波变换和带通滤波,残留大量的有效信号成分,说明Cycle-GAN和传统方法在压制随机噪声的同时均衰减了有效信号能量。

图8 残差噪声F—K谱图:(a) 纯净噪声F—K谱图;(b) A-CGAN残差F—K谱图;(c) Cycle-GAN残差F—K谱图;(d) 小波去噪残差F—K谱图;(e) 带通滤波去噪残差F—K谱图Fig.8 Residual noise F—K spectrum: (a) pure noise F—K spectrum; (b) A-CGAN residual F—K spectra; (c) Cycle-GAN residual F—K spectrum; (d) wavelet denoising residual F—K spectrum; (e) Band pass filter denoising residual F—K spectrum
3 实际地震数据去噪应用
为了验证A-CGAN的实际应用效果,使用A-CGAN的注意力去噪器、Cycle-GAN去噪器、小波变换、带通滤波器处理实际深反射地震数据。由于在实际深反射地震勘探过程中噪声一直存在,纯净地震记录无法获得,相应的SNR、RMSE也无法计算。因此对于实际深反射地震数据,通过观察去噪结果中同相轴的连续性判断去噪结果的优劣。图9显示了某区的深反射地震数据,从图中可以看出有效信号受到大量随噪声的干扰,同相轴连续性差,有的完全淹没在噪声中难以识别。分别使用A-CGAN注意力去噪器、Cycyle-GAN去噪器、小波变换、带通滤波器处理实际深反射地震数据,四种方法的去噪结果如图11a—d所示。从图10中可以看出,图10a经过A-CGAN处理后的深反射地震数据整体背景变得较为清晰,去噪效果提升明显,对随机噪音污染压制的更加彻底,隐藏在随机背景噪声中的有效信号突出显现,地震数据同相轴更加清晰,能量更集中(如图中箭头所示);从图10b可以看到Cycle-GAN有一定的弱信号恢复能力,但同相轴连续性比A-CGAN差;图10c中小波变换滤波对随机噪声的处理效果不佳,去噪后的深反射地震数据中仍存在大量的随机噪声,且对弱有效信号的保幅性差,导致去噪后的记录同相轴连续性仍然很差;图10d中带通滤波器去噪结果中同样存在大量背景噪声,无法较好地恢复弱有效信号同相轴的连续性。
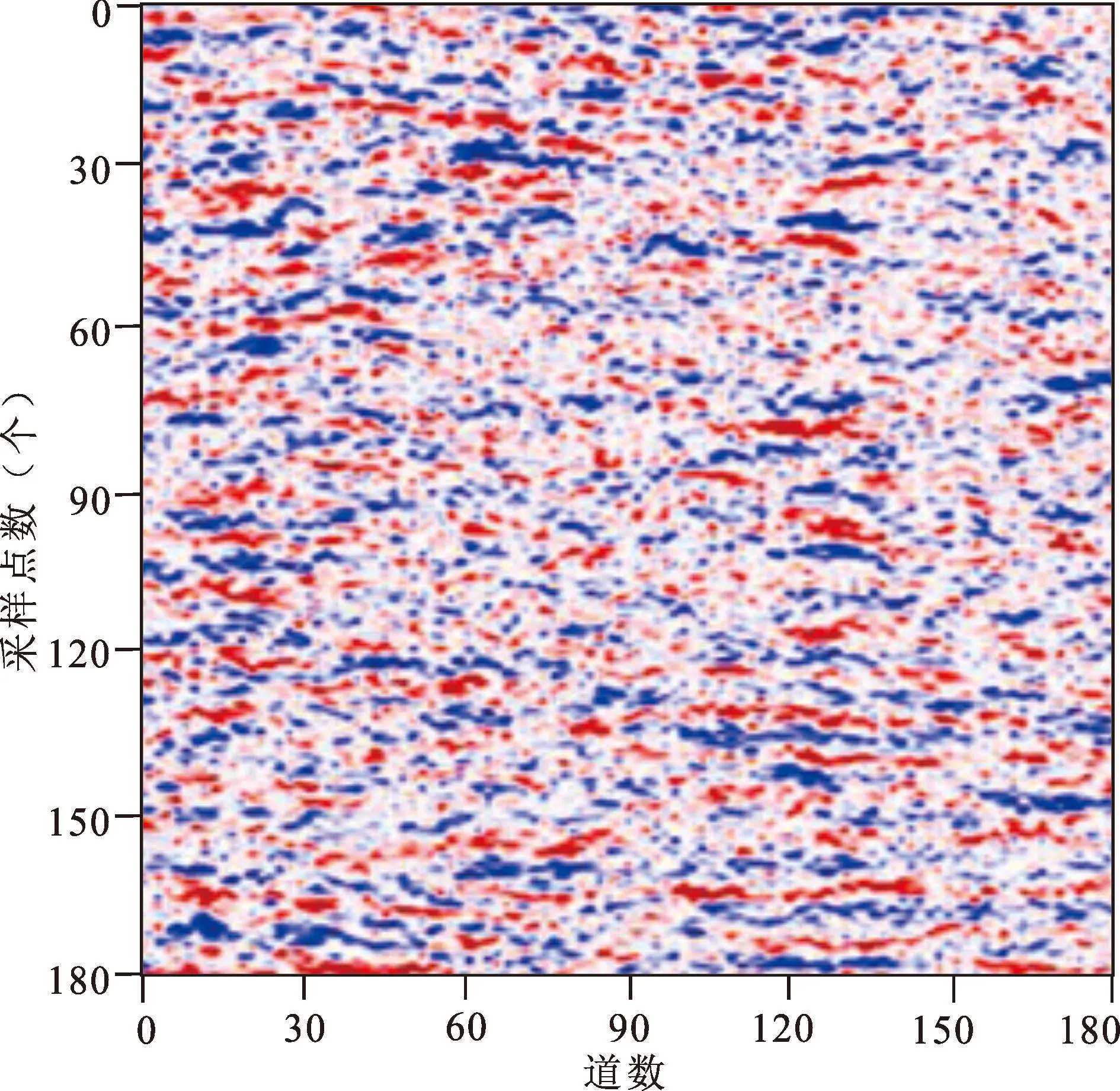
图9 实际含噪深反射地震数据Fig.9 Actual deep reflection seismic data with noise
4 结论
针对有监督学习网络通常需要构建成对数据,对数据集要求高的问题,笔者等基于Cycle-GAN域映射思想降低网络训练对数据集的要求。通过改进Cycle-GAN网络结构和损失函数训练出适用于深反射地震数据随机噪声压制的神经网络。笔者等提出的主要改进包括:在Cycle-GAN的生成器中加入注意力机制提升生成器特征提取能力;在Cycle-GAN鉴别器中使用块判别思想提升其鉴别能力;在损失函数中加入感知一致性损失,促进纹理细节的恢复。最后,通过在合成深反射地震数据和实际深反射地震数据上对网络效果进行测试,从时域去噪结果、去噪后的残差图、频域去噪结果、频域残差图等多个方面对A-CGAN进行综合评估。无论对于合成地震数据还是实际地震数据,笔者等提出的方法都取得了优于未改进去噪方法和传统去噪方法的效果。
当前的去噪效果虽然比未改进方法、小波变换、带通滤波等方法有较大的提升,但是在其他领域的去噪方法中,经常会在网络中加入多尺度结构用于加深网络层数、改变网络参数以提升网络的泛化能力和去噪效果。在后续的研究中,将进一步尝试在深反射地震数据去噪网络中加入多尺度变换结构,试验其与深反射地震数据的匹配度,提升去噪效果。

