阻容分压型电子式传感器幅频／相频特性的研究

李靖鑫 朱梓豪 宋昊阳 杨维婷 马梓焱 李佯洋

（1.云南电网有限责任公司曲靖供电局 2.西安兴汇电力科技有限公司）

0 引言

智能电网通过远距离高压架空输电线路输送强大电力，架空线路穿山越岭、环境恶劣，极易发生故障。一旦发生故障，造成供电中断，需要精确故障定位以便及时抢修，快速恢复供电。本项目对行波采集传感器提出了新的的融合应用创新要求，提升了架空线路在线巡监及精确故障定位技术与装备水平，解决了行波信号采集难，精度低等技术难题。本文重点研究阻容分压型电子式传感器的幅频／相频特性。验证不同采样电阻、采样电容对阻容分压型电子式传感器幅频、相频等参数的影响。

1 电子式电压传感器概述

从本质上来讲，电子式电压传感器是一种将模拟量进行采集最终实现就地数字化的装置。电子式传感器［1-2］和传统的电磁式互感器比较起来，具有以下诸方面的优点。

（1）绝缘性能好，重量轻，造价低。电子式传感器绝缘相对简单，使用具有绝缘性能的石英或塑料光纤用来作为高电压侧与低电压侧之间的信号传输介质，由于不采用导电的铁锌作为传输介质，因此大大简化了高压互感器［3］中的内绝缘结构，使整个电子式传感器体积小，重量轻，造价低。

（2）不含铁心，无磁饱和、铁磁谐振。电子式传感器没有铁心，不存在饱和问题，因此其暂态性能是传统互感器所不能比的，从而保证了各类保护测量的准确性，提高了保护装置的正确动作率，保证电网的安全运行。

（3）频率响应范围宽。电子式传感器的频率响应可达到10MHz以上。电子式传感器可以测出高压电力线路的载波，还可进行暂态电压，高频电压与直流电压的测量。

电子式传感器具有如此多的优势，在不同电压等级的智能变电站中被应用的情况越来越多，得到了国内外学者和工程界人士的广泛重视和认可。同时，在智能电网建设中，这种新型的互感器在不久的将来有望取代传统互感器，对改善电力系统稳定性和新型保护原理的发展起到了很大的促进作用。

2 研究内容

2.1 阻容分压型电子式传感器暂态特性研究

2.1.1 采样电阻对阻容分压器暂态特性的影响

阻容分压型电子式传感器数据为：PT中电容分别为630pF、1.94μF；采样电阻为5Ω；采样电容为0.1μF。因此根据阻容分压器结构传递函数，将数据带入可得：num＝［0 0 0.00000000063 0］；den＝［0 0 0.00000010063 0.2］。

由于PT中电容的数据已经为固定值，故在此对阻容分压器的采样电容和采样电阻进行分析，将采样电阻定为5Ω、50Ω、500Ω。则对应的传递函数系数数组为：den＝［0 0 0.00000010063 0.2］、den＝［0 0 0.00000010063 0.02］、den＝［0 0 0.00000010063 0.002］，画出此时波特图如图1所示。

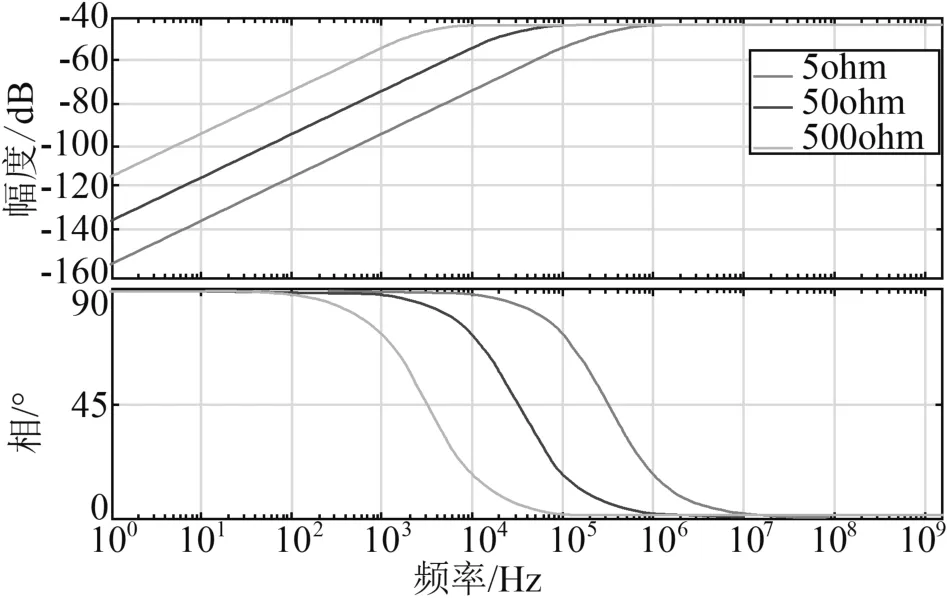
图1 不同采样电阻下阻容分压传感器的幅频／相频特性（幅度）

可以看出，幅频特性曲线为斜率为＋20dB／dec（分贝／十倍频）的直线，相频曲线为与频率无关的直线，这说明阻容分压器的二次信号输出是正比于输入的微分。为对二次测量信号强度能够有更加直观的体现，将幅频特性曲线纵轴 （幅度）转为绝对值，则图1可转化为如图2所示。

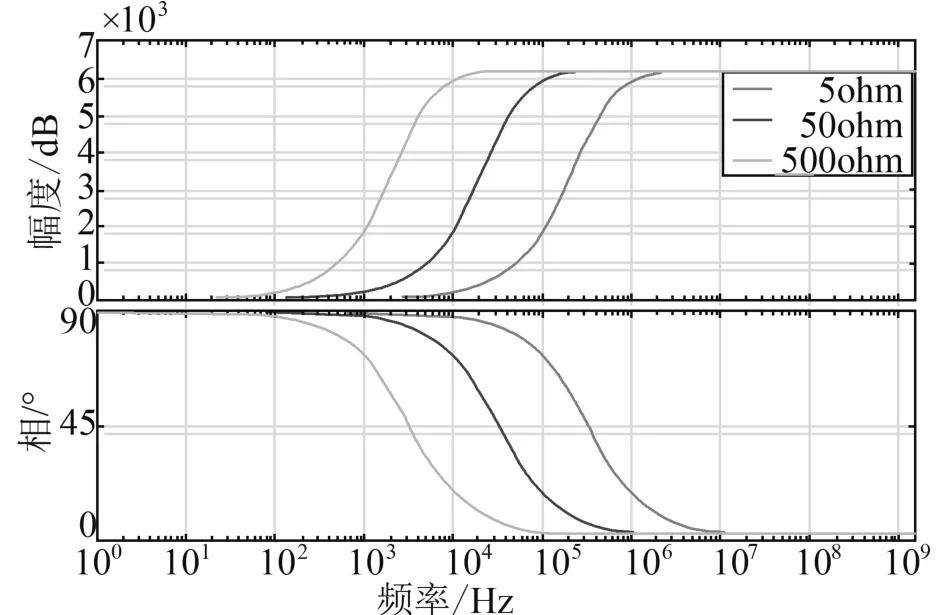
图2 不同采样电阻下阻容分压传感器的幅频／相频特性（绝对值）

可以看出，当频率较低时阻容分压器的幅频特性曲线接近于零，这说明在低频时阻容分压器二次测得的信号幅值非常小，在高频时采样信号近似满足高压侧电容和电容的分压比关系（阻容分压器可理解为高通滤波器）。

除幅频特性之外，我们还应关注相频特性，可以看到相频曲线在低频时近似是数值为90的一条直线，在高频时是一条为0的直线，在中间频率则呈现出渐变的规律。相频特性的物理意义在于：不同频率的信号通过采样之后的信号与原始信号的相位差。例如对于目前认为较为常见的10～100kHz，我们自然希望互感器的相频特性中对于该频段信号的相位变化能够尽量维持在较小范围，这样便能保持信号相位失真较小，便于后续的测量。

故可得出结论，对于阻容分压型电子式传感器（不带积分电路），可以通过改变采样电阻的阻值修改传感器的采样频率起始值也就是我们所关心的采样频率范围。当采样电阻增大时，采样起始频率减小，反之采样起始频率增大。

为印证上述采样电阻对阻容分压传感器暂态特性的影响规律，将采样电阻再次调小，观测模型波特图的变化。将采样电阻分别设为0.2Ω、1Ω及5Ω，作出此时阻容分压传感器的波特图如3所示：

从图2和图3的分析中可知，不论是幅度还是绝对值，虽然两者图像不同但是表达出的规律是相同的。可以看到随着采样电阻的减小，系统采样的起始频率随之上升。

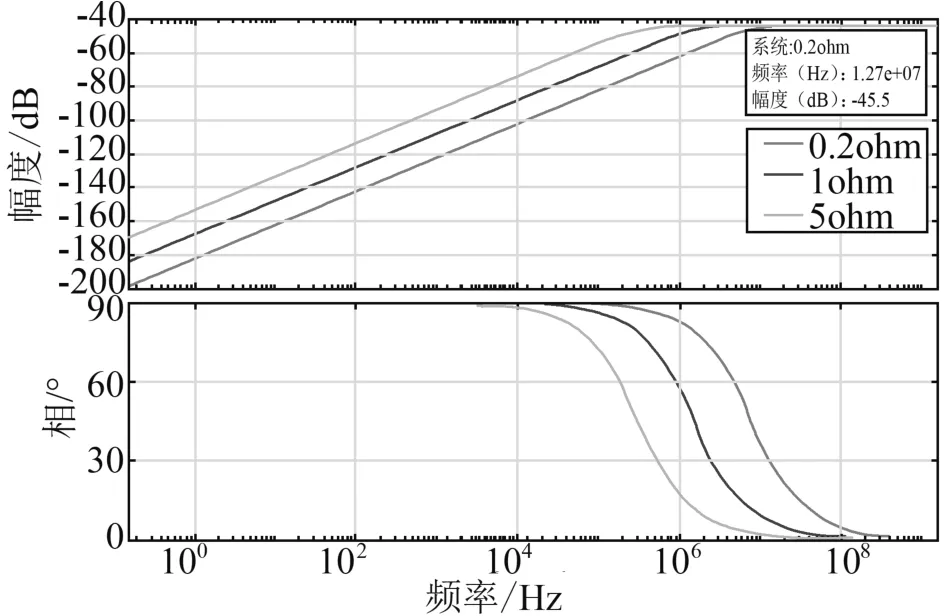
图3 减小采样电阻后阻容分压传感器的幅频／相频特性

采样电阻的大小虽然会对采样起始频率产生影响，但是不会影响到最终的变比，故完全可以通过改变采样电阻的大小来控制阻容分压传感器的采样起始频率进而控制传感器的采样范围，当然在对采样变比要求不是特别严格的条件下，可对采样电阻和采样电容共同调整从而改善暂态特性。

2.1.2 采样电容对阻容分压器暂态特性的影响

若对采样电容进行分析，则需采用控制变量法。首先对采样电阻的大小进行确定，电阻的阻值定为目前选择的5Ω。而采样电容目前定值为0.1μF，将采样电容增大，分析采样电容增大对暂态特性的影响。对于5Ω、0.1μF阻容分压器，其传递函数为num＝［0 0 0.00000000063 0］；den＝［0 0 0.00000010063 0.2］，因此对于采样电容：采样电容为1μF时：num＝［0 0 0.00000000063 0］；den＝［0 0 0.00000100063 0.2］；采样电容为10μF时：num＝［0 0 0.00000000063 0］；den＝［0 0 0.00001000063 0.2］。作出此时阻容分压器传递函数波特图如图4所示：

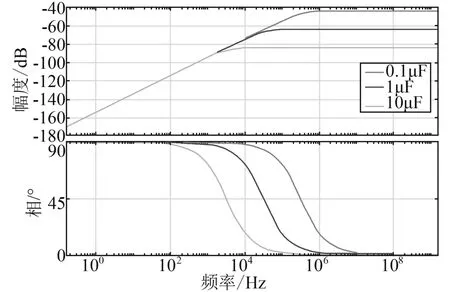
图4 不同采样电容下阻容分压传感器的幅频／相频特性

从图中可以看出，随着采样电容的增大，采样起始频率逐渐减小。值得一提的是采样电容的大小同样会影响互感器变比。

采样电容为0.05μF时：num＝［0 0 0.00000000063 0］；den＝［0 0 0.00000005063 0.2］；

采样电容为0.01μF时：num＝［0 0 0.00000000063 0］；den＝［0 0 0.00000001063 0.2］；

以上述传递函数数组作出采样电容为0.1μF、0.05μF、0.01μF时所对应的波特图如图5所示。

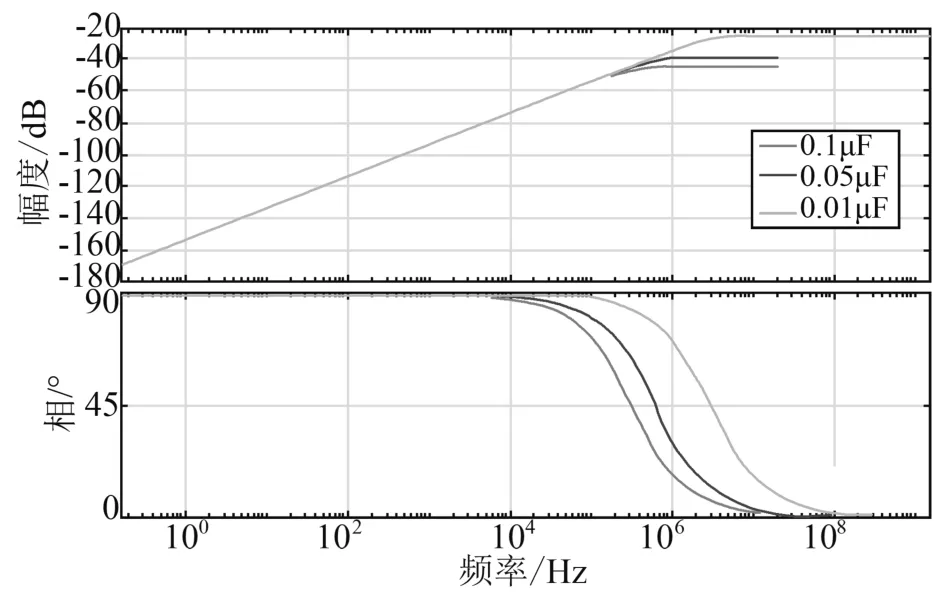
图5 采样电容不断减小时阻容分压传感器的幅频／相频特性

从上述分析中，针对阻容分压型电子式传感器，可以总结出采样电阻和采样电容对幅频特性的影响如下：

（1）可以将阻容分压型电子式传感器理解为高通滤波器，原理上是由于电容阻抗值随频率的变化导致采样时变比的变化，低频时采样数值非常小甚至难以采集到数据，高频时采样逐渐趋近于计算变比并稳定于该数值；

（2）采样电阻增大时，传感器起始采样频率减小。采样电阻减少时，传感器采样频率增大。并且采样电阻大小不影响互感器变比；

（3）采样电容增大时，传感器起始采样频率减小。采样电容减少时，传感器采样频率增大。并且采样电容的大小影响传感器变比，采样电容越大变比越小，采样电容越小变比越大。

2.2 阻容分压型电子式传感器幅频特性

有关幅频特性、相频特性及截止频率的相关描述，现已知这个系统的传递函数，求出其幅频特性和相频特性。

令s＝jω，则式（1）可以写为：

幅频特性为｜H（jω）｜，则：

相频特性：对于任意一个复平面的函数，均可写成A∠φ的形式。而对H（jω）也是如此，其传递函数是两部分相乘，则对于复平面来说相角则分别为两部分相加，于是有如下计算公式：

则根据式（4）计算可得：

当然式（5）也可进行化简，但是为了体现出相频特性的构成，本文档中均写为如式（5）的形式。而对于截止频率，截止频率的定义为：当保持输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍，即用频响特性来表述即为－3dB点处即为截止频率。

对于幅频特性曲线中纵轴的幅度（Magnitude），其单位为dB，一般而言其计算公式为：

当幅度为－3dB时，对应的｜H（jω）｜＝或｜H（jω）｜2＝，则由此可得出该系统上下限截止频率为：

3 结束语

由上述分析可知，传感器的暂态特性主要包括幅频特性、相频特性以及截止频率。对于行波测距而言，传感器对信号的传递必须尽可能满足如下两个条件：

（1）根据幅频特性：传感器要尽可能满足对应在采样信号频率的频段内，采样幅值尽可能较大，保证至少能够采到数据。

（2）根据相频特性：传感器要尽可能满足对应在采样信号频率的频段内，相频特性曲线尽可能保持“直线”，即相频特性变化较小。

关于阻容分压型电子式传感器结论，根据本文档分析内容，阻容分压式传感器参数对暂态特性的影响可总结结论如下：

（1）采样电阻的大小只影响幅频、相频特性左移或右移，不影响采样变比。当采样电阻增大时，幅频、相频特性曲线左移；反之幅频、相频特性右移。

（2）采样电容的大小不仅影响幅频、相频特性，还会影响变比。当采样电容增大时，幅频、相频特性曲线左移，采样变比变小；反之幅频、相频特性右移，采样变比增大。