初中数学跨学科主题学习的设计与实施
程晓亮 左瀚文 林殿吉

摘 要:当前,各学科都在探索立足于本学科课堂开展的跨学科主题学习活动。数学学科具有高度的抽象性、严谨的逻辑性、广泛的应用性,构建适合数学学科的跨学科主题学习设计与实施方式具有重要意义。立足于初中数学的跨学科主题学习可以“三会”为宗旨、以“四基”为基石、以“问题”为核心设计学习模型,在实施过程中,教师要注意引领问题导向,推动合作探究,扩展评价交流,并以“问题与情境”“知识与技能”“思维与表达”“交流与反思”四个方面的表现为支撑进行评价反思。
关 键 词:跨学科主题学习;初中数学;数学核心素养;跨学科情境
引用格式:程晓亮,左瀚文,林殿吉.初中数学跨学科主题学习的设计与实施[J].教学与管理,2024(04):39-42.
《义务教育数学课程标准(2022年版)》明确建议以跨学科主题学习的方式开展综合与实践活动。跨学科主题学习的提出是对中国学生发展核心素养的深刻践行,而具备核心素养是中国学生学习发展要实现的目标。数学学科在科学精神、实践创新、学会学习等维度具有不可替代的价值,如何在数学课堂中发展学生核心素养?跨学科主题学习是一个重要的方式。数学的一般性和应用的广泛性决定了数学与真实生活、与其他学科有着密切联系。当今时代,无论是在科学技术领域,还是在人文社科领域,数学都发挥出越来越大的作用。然而,传统数学教学受工具理性价值影响,往往将解题技巧、速度和准确度作为数学学习效果评价维度,导致数学与实际生活存在较大的隔阂。学生既不清楚数学从何而来,也不完全明白数学能够用在何处。跨学科主题学习可以有力地与常规课堂形成互补关系。在跨学科主题学习中,学生将日常所学应用到真实的、跨学科的问题解决过程中,增进对数学的认识、发展核心素养。
跨学科主题学习是增强学生主体参与感的有力方式。在常规课堂中,教学多以教师讲学生听的方式开展,学生的能动性并未充分释放,学习被动进行。然而在跨学科主题学习中,教师角色转变为推动者而非主导者,学生以主体参与者的身份进行思考讨论,调动多方面的知识、经验,充分发挥自我能动性。当学生体会到自己在问题解决中的力量,就能提高数学学习兴趣,重新审视诸多与数学学习有关的非智力因素。在此过程中学生的主体意识得到培育,逐渐意识到数学与真实生活、与其他学科的关系,又进一步激发出主体动能。
《义务教育课程方案(2022年版)》颁布以来,各学科都掀起了跨学科主题学习的实践热潮,然而从当前已发表的论文来看,多数实践集中在物理、化学、生物、地理等学科,立足于数学的跨学科主题学习研究较少。当前的实践中存在一些不容忽视的问题。例如课程的拼盘化、形式化和浅表化。如何依据课程标准设计实施立足于数学的跨学科主题学习活动?这是迫切需要回应的问题。
一、数学跨学科主题学习的设计模型
立足于数学的跨学科主题学习本质上是一类问题解决活动,而与解题活动不同的是它旨在解决一类特殊的问题,这类问题不是常规的良构题目,而是源于真实生活的、与其他学科关联的问题。因此,数学跨学科主题学习设计的关键就在于对这类问题的锚定。
1.以“三会”为宗旨的设计理念
《义务教育数学课程标准(2022年版)》中提出了培养学生“会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界”(以下简称“三会”)。“三会”是数学学科培育学生核心素养的统领性表现。“会用数学的眼光观察现实世界”意味着学生要调动几何直观、空間观念和数感、量感等数学素养,从纷繁复杂的现实生活情境中抽象出数学问题,进而借助数学视角观察现实世界。由于现实的多维性,抽象的过程自然与现实生活以及其他学科产生多种联系,知识不再是孤立存在而是形成了立体的网状结构。“会用数学的思维思考现实世界”意味着学生要借助推理和运算等数学素养得到由现实世界表征出来的数学问题的解。这样的数学问题由自我逐步构建,因此能激发探究的能动性,学生解决问题的潜力由此得到释放。“会用数学的语言表达现实世界”意味着要借助数学符号、数学模型等表达现实世界某方面的特征。由数学推理和数学运算得到的问题的解并不是一个抽象的数字或公式,它明确地表达了现实世界某一问题的特征。因此,必须将解重新带回现实世界赋予其内涵,再次与真实生活建立联系。“三会”既体现了数学学习的意义,也蕴含着数学学习的方法,以“三会”为引领能够设计出有“数学味”的跨学科主题学习活动。
2.以“四基”为基石的设计起点
数学基础知识、基本技能、基本思想、基本活动经验(以下简称“四基”)是课程改革凝聚起来的宝贵经验,是发展学生核心素养的有效载体。立足于数学学科的跨学科主题学习活动的设计起点就来自于对“四基”的准确把握。数学基础知识、基本技能主要指数学学科中的一些结果性知识、客观事实、运算程序等。离开了基础知识和基本技能的跨学科主题学习活动可能会失去生命力,也无法激发学生思考数学与实际生活的关联。数学基本思想和基本活动经验则是学生在学习活动中内化于心的体验和感悟,跨学科主题学习的目标就是通过活动增加学生对数学的真实感受,从中体会用数学的眼光看世界的方法与价值及其背后蕴含的思想。基于此,在选择跨学科主题学习中的问题时,就应该首先考虑活动中是否涉及与学生当前认知相匹配的基础知识和基本技能,是否能促进学生深入思考数学问题背后的思想,是否能够积累充分的活动经验。
3.以“问题”为核心的设计思路
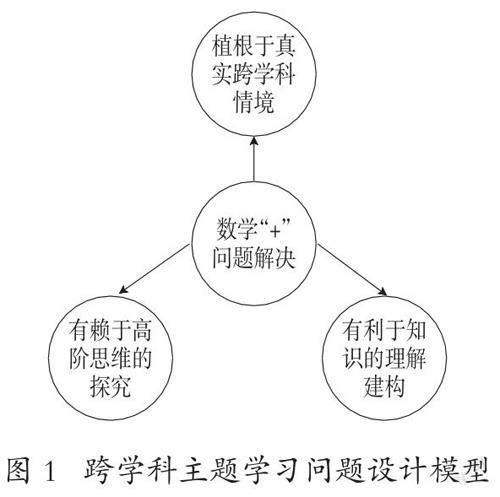
跨学科主题学习是培养学生“发现问题、提出问题、分析问题、解决问题(以下简称四能)”的重要步骤。其中,问题是跨学科主题学习的核心,立足于数学的跨学科主题学习核心就在于问题的锚定,跨学科主题学习的设计过程就是锚定适切问题的过程。有学者提出将数学和科学整合的Authentic Int-egration模型,该模型认为跨学科整合中任务是关键,知识的发展、综合与应用和协作探究促进高阶学习构成了基础,适用于现实情境作为重要补充。如图1所示,本研究将该模型与“三会”理念相结合,以“四基”为出发点,提出跨学科主题学习中问题应具备的特征:植根于真实跨学科情境,有赖于高阶思维的探究,有利于知识的理解建构。
(1)植根于真实跨学科情境。“三会”带给我们的重要启示是数学与现实世界密切相关,无论是“数学眼光”“数学思维”还是“数学语言”,都离不开对现实生活的关注与思考。离开了现实的数学教与学难以激发学生与生俱来的探究欲、好奇心。然而,数学课堂中通常呈现给学生的数学往往是已经完成对现实世界抽象的“成品”,相当一部分同学并不了解数学来自何方、用于何处,导致数学学习兴趣不高。基于此,跨学科主题学习所要探究的问题必须首先植根于真实跨学科情境之中。“真实”指问题可以源于学生的生活经验或者问题情境能够由学生轻松再现,例如,“探究手电筒照射在墙壁上形成的图形所蕴含的规律”这一问题,所需工具仅仅只有手电筒,学生容易再现该问题情境,获得具身体验,从而激发探究思考的主动性。“跨学科”指问题可以来源于其他学科。数学的抽象性决定其应用的广泛性,自然科学和社会科学中都蕴含着诸多可以借助数学进一步深入理解的问题。例如,“如何理解地轴与公转轨道面的夹角导致太阳直射点在南北回归线之间的移动”,这一地理学科的问题就可以借助数学中三视图的概念得到简明的解释。
(2)依赖于高阶思维的探究。跨学科主题学习中的问题所具备的另一重要特征是探究性。问题解决路径并没有直接的经验可供借鉴,它要求学生必须探索各种可能的方案,从而找到正确的出口。这样的探究有赖于分析与综合、评价、创造的高阶思维,仅仅依靠识记等低阶思维是不足以解决问题的。由于问题植根于真实跨学科情境中,其表征开始时并不具备明确的学科特征,因此学生必须调动各方面的信息做出综合决策,以分析适合于解决该问题的知识究竟有哪些。
依賴于高阶思维的探究具有合作性和目标性两大特征。合作性指问题往往仅凭一人之力无法解决,因为所涉及的学科、生活经验、操作步骤较为复杂,因此小组合作是一种较为适宜的问题解决开展方式,这样既能集思广益更好地解决问题,又能培养学生沟通交流的能力,形成团结互助的班级氛围。目标性指探究活动并非无方向的讨论,它明确指向问题解决,问题的答案虽然并不一定是绝对唯一的,但依然有明确的方向性。学生在跨学科主题学习中不再是被动的知识接受者,仅仅依靠听讲、识记知识、套用解题模版等不再有效,它要求学生分析问题的症结、综合所学的各种知识做出判断与评价,在整个活动中反思自己的知识,进行批判性思考,使高阶思维在探究中得以发展。
(3)有利于知识的理解建构。问题的选择还应当满足有利于知识的理解建构特征。这里的知识主要指:第一,义务教育数学课程标准明确要求的数学基础知识、基本技能、基本思想方法;第二,解决该问题要用到的数学知识应基于学生的旧知。如果一个问题的解决要用到学生尚未学到的数学知识,就无法调动起学生的已有经验,也就无法将已有的知识建构为系统的知识网络,反而会加重学生的认知负担。
立足数学学科的跨学科主题学习不是实验课,也不是手工课,它本质上仍旧是数学课,如果活动中所涉及到的数学仅仅是加减乘除计算,难免会淡化数学应有的“味道”。因此在设计、选择问题时应该考虑解决该问题是否增进了学生对所学数学的理解,例如增进对某一概念、定理、公式和应用场景的理解;活动是否有利于学生建构属于自己的知识体系,例如将方程与函数联系在一起考虑;活动是否有助于学生应用所学数学知识解决特定场域中的实际问题,例如启发学生观察思考生活或其他学科中类似可以应用数学的现象。数学课堂中的跨学科主题学习必须考虑问题与数学学科本身的关联性,这样的关联可以是与某个具体数学知识的相关性,也可以是与数学技能或者数学思想方法的相关性。
二、数学跨学科主题学习的实施模型
立足于数学的跨学科主题学习旨在探究一类特定问题的解,其实施流程与探究学习的思路存在诸多共性。基于此,本研究构建了以教师角色转变为特征的跨学科主题学习实施模型,如图2所示。
1.教师引导的问题提出环节
如前所述,立足于数学的跨学科主题学习关键在于问题的选择。问题的确定可能存在两种路径:一种是由教师提前预设,另一种是由全班头脑风暴后即时生成。无论是哪种路径,教师的引导者角色都是至关重要的。如果教师已经预设好一个问题,那么以何种方式将问题恰切地抛给学生并引发大家对这一问题的研究兴趣非常考验教师的设计能力;如果在班级讨论后再聚焦到待解决的问题,那对教师的全局掌控能力和对诸多生成性资源的迅速决策能力要求更高。问题提出环节的目的是聚焦待解决的问题,如果教师将这一问题直接呈现给学生,隐去前因后果以及实际背景,这既不利于充分调动学生的积极性,也无法满足学生的好奇心和探究欲。因此,基于路径一的问题提出环节,教师创设合适的情境,逐步引导学生进入到欲探究问题的空间是必要的。基于路径二的问题提出环节,教师引导学生在诸多想法之中确定与数学密切相关且值得继续深入探究的问题考验着教师的数学眼光和教学智慧。
2.教师推动的合作探究环节
明确提出要研究的问题后,跨学科主题学习就进入到以小组为单位的合作探究环节。本环节学生以小组合作的形式开展探究活动,各小组通过交流讨论,进一步明确问题、制定可能的解决方案、完成任务分工等等。教师在这一阶段中不应出现主导学生探究活动进程的行为,例如:人为加快学生的探究步伐、为提高课堂效率而给学生提供过多支架降低思维难度等等。这样会导致整个课堂活动看起来非常顺利,但事实上学生并没有经历足够的思维历程,也就丧失或降低了跨学科主题学习活动应有的育人价值。教师在本环节的主要角色应是学生合作探究的推动者,可以通过质疑追问等方式激发学生深入思考,对不愿或不会与他人合作的同学开展有效的干预,把握小组合作探究重心不发生偏移。教师角色的转变对教师而言具有较高的挑战性,跨学科主题学习活动的顺利开展需要教师既能促进学生的自主深入探究,又能使课堂纪律不会失去控制,这对教师的综合能力提出了更高的要求。
3.教师参与的评价交流环节
学生在以小组为单位开展合作探究后,需要整理本组的成果进行汇报。这里的成果与项目式学习中要求的某一实物作品并不完全等同。立足于数学的跨学科主题学习活动成果可以是一个是实物作品,也可以是一个问题解决方案,还可以是对一个现象的数学化解释等。对小组成果的评价应由两大主体(教师和学生)共同来完成。学生既要进行自我评价,也要评价其他小组的表现,评价的维度可以是问题解决方案是否完善、汇报是否详略得当、小组合作是否充分等。教师是评价交流环节的另一主体,教师的角色不是主导者,但教师应有效参与到评价环节中来。教师能够站在另一个角度来评价学生在整个跨学科主题学习中的表现,因为学生在活动中只关注到局部而忽视了整体,而老师却拥有类似局外人的眼光,他可以发现学生在整场活动中出现了哪些闪光点、有哪些不足之处、对数学的思考与应用是否深入等等。教师的评价对学生发展至关重要,对教师本人也具有挑战性,如果教师评价得当,可以激发学生反思,为下次跨学科主题学习活动做好铺垫,学生会在一次次这样的跨学科主题学习中发展高阶思维、增进学科理解、提高与人交流合作的能力。反之,如果老师只是不痛不痒、蜻蜓点水一般地给出评价,那么本次活动能产生的教育效果可能就会大打折扣,学生也许只会留下这类课“好玩儿”的印象而无法激发深入的思维活动。
4.以“四大表现”为支撑的评价反思
高中数学课程标准依据“四大表现”来刻画学生的数学核心素养发展状况,立足于数学学科的跨学科主题学习目标是发展学生的核心素养进而落实“三会”的育人理念。借助“四大表现”框架,能够评价反思跨学科主题学习的设计与实施是否促进了学生核心素养发展。
(1)问题与情境。跨学科主题学习倡导将问题放置于真实的情境之中,可以是现实情境、数学情境、科学情境等。真实是跨学科问题情境的关键要素,意义在于学生能够基于自己已有的知识和经验等再现问题,能够亲身体会到问题的真实存在性,只有这样才能激发学生的能动性。因此,评价一个跨学科主题学习是否合适的首要标准就是是否营造出一个能让学生感受到的真实问题情境。
(2)知识与技能。跨学科主题学习中问题解决必须要用到与学生认知水平相匹配的数学学科的基础知识和基本技能,学生在解决问题的过程中有意或无意地使用了课堂中所学的数学,如此一来就能感受数学与生活的关联性,进而提高学习兴趣。如果一个跨学科主题学习不涉及学生的基础知识和基本技能,那就无法有效激发学生对数学的深度思考,失去了应有的育人价值。
(3)思维与表达。如前所述,跨学科主题学习有赖于高阶思维的发展,仅仅记忆知识是无法解决问题的。问题的解决需要综合分析已有条件,将知识迁移到陌生情境之中,如果跨学科主题学习所选择的问题仅仅依靠低阶思维就能完成,那就无法提高学生的思维品质,培养高阶思维。此外,将思考结果严谨准确地表达出来也是一個必不可少的要求,这是现代社会人与人交流越来越密切的大背景下必须具备的素养。因此,评价跨学科主题学习的设计与实施是否达到目标的重要维度就是学生在活动中思维与表达能力是否得到发展。
(4)交流与反思。这是跨学科主题学习的一个重要环节。从建构主义的视角来看,知识是在与他人的交流与合作中逐步建立起来的,因而交流反思环节必不可少。交流与反思的内容可以是对问题解决过程所涉及的数学概念、思想方法或其他学科内容的理解,也可以是小组合作的经验分享等等。只有具备了这一环节,跨学科主题学习活动才能完整地体现育人价值。
参考文献
[1] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[S]. 北京:北京师范大学出版社,2022:16-17.
[2] 吴现荣,牛伟强.论数学素养与核心素养的关系[ J ].教育评论, 2018(08):135-138.
[3] 曹一鸣,刘冰.《义务教育数学课程标准(2022年版)》修订的基本原则[J].教育评论,2022(05):17-23.
[4] 王尚志.参与数学课程改革的经历与感悟[J].基础教育课程,2021(19):4-10.
[5] 黄友初.小学数学综合与实践教学的内在逻辑与实施要点[J].数学教育学报,2022,31(05):24-28.
[6] 郭华.跨学科主题学习及其意义[J].文教资料,2022(16):22-26.
[7] 田娟,孙振东.跨学科教学的误区及理性回归[J].中国教育学刊,2019(04):63-67.
[8] 郭衎,曹一鸣.综合与实践:从主题活动到项目学习[J].数学教育学报,2022,31(05):9-13.
[9] Treacy P. A conceptual framework for integrating mathematics and science in the secondary classroom[J]. SN Social Sciences,2021,1(06): 1-17.
[10] 中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[S]. 北京:人民教育出版社,2020:74-78.
【责任编辑 王泽华】

