水平井泵送桥塞工具串可通过性研究

苏 鹏，冯梓波，刘永升*，侯子扬，李渭亮

（1.中国石化西北油田分公司石油工程技术研究院，新疆 乌鲁木齐 830011；2.中国地质大学（北京）工程技术学院，北京 100083）

0 引言

近年来，随着非常规油气田勘探与开发技术不断革新，针对页岩气、页岩油、致密油等非常规致密储层的水平井泵送桥塞分簇射孔工艺取得了广泛应用［1-4］。该工艺主要通过水力泵送的方式，把携带有由可钻桥塞和多级射孔枪连结成的工具串输送到指定位置，在桥塞完成坐封后，上提射孔枪到射孔位置进行多次射孔，最后提出射孔枪，进行水力压裂，多次重复此操作直到完成全井段的射孔压裂［5］。

尽可能多的携带射孔枪使每次下放可进行多次射孔，可极大提高每口井射孔压裂的效率。由于井眼轨迹曲折复杂多变，工具串下放卡阻问题突出。保证工具串泵送完成由诸多因素影响，包括泵送排量，井筒与工具间隙等。如果工具串携带射孔枪过多，则其无论如何也无法通过弯曲井段完成泵送。若下放前未对工具串配置进行精准控制，极有可能导致工具串卡死从而带来不必要的经济损失并极大降低生产效率。因此在进行泵送设计之前，需合理的控制其长度配置。

目前国内针对井下工具串通过性的研究尚无考虑工具串的具体形状特点，只是将其简化为圆柱体进行分析计算［6］。但泵送桥塞工具串并非规则的圆柱体［7］，依据该简化方法所得模型进行长度计算会导致结果偏小；同时，对工具串和井筒进行几何分析时，未对工具串泵送遇阻时与管壁的接触点进行分析，默认于射孔枪部分和管壁卡死［8］。而实际工程中接触点还有可能位于桥塞工具部分，缺乏接触点分析会使计算结果不准确；泵送工具串由于其截面长宽比过大，现有研究未对其在弯曲井段受力弯曲的特性进行计算分析，会使计算长度比实际可通过长度偏小。

本文将对泵送桥塞工具串进行泵送遇阻接触点分析，并根据接触点对其受力分析，结合其材料强度，建立一种考虑其受力弯曲的工具串可通过最大长度计算方法，由于磁定位器以及桥塞等部分长度固定，因此得出其最大长度，即可确定射孔枪配置方案。最后通过理论分析和数值模拟的方法对实际案例进行计算，并进行相应的影响因素分析。

1 工具串通过性判别准则

1.1 模型几何特征分析

泵送桥塞工具串由多节相连成串的管状工具组成［9］，最上部为与缆线相连的磁定位器，用于井下工具串定位与射孔位置定位，该部分直径较小；通过转换接头与磁定位器相连的是多级定向射孔枪，每级射孔枪长1～2 m，一次可携带多个射孔枪进行多级分簇射孔，该部分一般为工具串中最长部分；最后部分为桥塞工具串，该部分包括桥塞送进工具，推筒和桥塞，桥塞工具部分为整个工具串直径最大部分［10］。

根据上述泵送桥塞工具串结构特点，如图1 将其简化为三段式几何模型，用于更精确的理论分析计算与数值模拟模型建立。

图1 桥塞工具串三段式简化示意Fig.1 Simplified diagram of bridge plug tool string in three stages

由于l1，l3长度固定，l2长度由射孔枪级数和型号决定，因此确定l2最大值，即可求确定可通过弯曲井段的工具串配置。

1.2 接触点确定

确定受力弯曲情况下可通过工具串最大长度，需先确定受力位置，即上端与工具串的接触位置。

如图2 根据上述三段式模型分析泵送桥塞工具串与套筒接触点。工具串下方与套管有两个接触点位置确定，为工具串前部和后部端点。

图2 泵送遇阻几何关系Fig.2 Geometric factors of pumping obstruction

三段式模型各段直径和长度具有以下关系：

l1长度与直径均小于l2，故l1上不存在接触点。工具串与管壁上侧接触点可分为两类，第一类接触点在l2段中部，为管壁与射孔枪接触所形成的接触点；第二类接触点在l3段前端，与桥塞工具边缘接触。判断接触点类型方法为：计算管壁与第一类接触点接触时，管壁与第二类接触点位置关系即可。O1与l2接触时，O1与桥塞工具相离，则可判断为第一类接触点；O2与l2接触时，O2与桥塞工具相交，则可判断为第二类接触点（参见图2）。

将两接触点在图中标为C1、C2，工具串的长度记为L，在狗腿度为κ的弯曲井段，井眼轨迹曲率半径为：

首先确定长度为L的工具串在l2段接触点C1与前端距离a：

如图2 所示，其与A点与管壁所在曲率圆圆心所连直线：

其中r1、r2、r3为工具串三段半径，前端到轴线中点距离记为a。计算两接触点连线与工具串轴线夹角表达式：

连接C1、C2并将该线段记为b，其表达式为：

计算管壁所在曲率圆内过C1且角度为θ的弦长记为c：

如果C2在该曲率圆内，则管壁在与l2相交之前已与l3相交，因此接触点为C2；同理如果C2点在该曲率圆外，则管壁在与l2相交时与l3相离，因此接触点为C1。对比b、c大小，有以下结论：

当c1＜b：接触点为C1，于l2段上；

当c2＞b：接触点为C2，于l3段上。

1.3 刚性可通过长度方程

确定该井内工具串遇阻时的接触点类型后，应确定刚性可通过最大长度从而确定手里弯曲下泵送桥塞工具串可通过最大长度。

经过判断如果为第一类接触点，由于β的表达式为包含L的函数，同时根据几何关系有sinβ=因此在第一类接触点下，刚性长度方程为：

如果为第二类接触点，则工具串的l3部分，即桥塞工具段与井壁有两个交点。l3部分轴线与井壁切线夹角为γ=0.5π-β，则根据桥塞工具部分在管中位置关系可得，为第二类接触点时，刚性长度方程为：

1.4 挠度方程

如图3 所示，分析工具串弯曲变形时，需考虑垂直于轴线方向的受力情况，摩阻力等部分外力在弯曲井段垂直于轴线方向的分力极小，因此不考虑其对可通过性的影响。将工具串自重及浮力合力在垂直于工具串变形前轴线［11］，且与接触点对工具串压力在同一平面上的分力看作均布荷载［12］，由于三段材料以及尺寸各不相同，可将其分别记为q1、q2、q3。第一、三段长度l1、l3已知，l2未知。将工具串两端支反力记为F1，F3，接触点处作用力最大值记为F2，接触点到桥塞底部距离为记d。

图3 弯曲井段工具串垂直轴线方向受力Fig.3 Force diagram for tool string in vertical axis direction for curved wellbore section

工具串弯曲变形越大，则可通过长度越长，因此在求解工具串可通过最大长度时F2可由射孔枪段弯曲强度求得［13］。

基于上述前提，建立平衡方程可得：

其中，d=bcosθ+l3，为第二类接触点时，d=l3；

如图4 所示，ω1、ω21、ω22、ω3为分为四段后每段的挠度。设工具串最大挠度位置在距离l2弯曲前轴线前端x处，由变形的对称性可知，工具串两端在x处挠度相同，均为最大挠度ω，因此有以下平衡关系：

图4 挠度叠加示意Fig.4 Deflection superposition diagram

因此可将其分为四段求解挠度表达式后叠加求解：

其中，EI——抗弯强度，E——弹性模量，I——截面惯性矩。

代入平衡方程整理可求得x关于l2的表达式：

其中：

因此工具串在弯曲井段最大挠度表达式为：

1.5 可通过最大长度

工具串刚性可通过长度L与弯曲变形情况下可通过最大长度Lω关系如图5 所示：

图5 刚性与弯曲变形可通过长度示意Fig.5 Allowable lengths under rigid and flexural conditions

L与Lω均相切于管壁内侧所在圆上，均相交于管壁外侧所在圆，焦点距圆心距离均为弯曲井段的曲率半径R1=5400/(πκ)，因此弯曲变形工具串曲率半径表达式为：

其中ω为最大挠度。根据几何关系计算可得弯曲变形工具串最大可通过长度表达式为：

由于实际生产中l1、l2已知，因此可由Lω求得射孔枪最大长度。该表达式所求最大长度为理论精确值，实际生产中应根据实际情况取5%～10%的安全余量，选用合适的射孔枪配置。

2 实例分析

针对上述工具串长度计算方法，以塔河超深碎屑岩TKC1-3H 井进行泵送桥塞射孔作业为例进行实例分析。该井最大狗腿度17.79°/30 m，且狗腿度变化幅度大。施工中选用9.05 m 泵送桥塞工具串，多次出现泵送遇阻现象。现将针对该案例进行理论计算以及基于数值模拟，分析其接触点位置以及可通过工具串最大长度，并进行包括狗腿度以及井筒直径的影响因素分析。

2.1 理论分析

该井数据及选用工具串尺寸数据如表1 所示：

表1 案例分析数据Table 1 Case analysis data

根据该井数据可知，该井最大狗腿度为17.79°/30 m，井斜角α=38.3o，若工具串能通过该处，则该工具串可通过整个井且不发生泵送遇阻。经计算，该处曲率半径为R=96.62 m，将包含L的表达式进行比较有c1＜b，因此可确定接触点为第一类接触点。

在确定泵送遇阻时接触点为第一类接触点后，进行工具串最大长度计算，A 点与管壁所在曲率圆圆心所连直线夹角β=arcsin [(R+r2+r1)/(R+D)]=88.84°，该井可通过刚性最大长度方程为：

求解得工具串刚性最大长度为：L=4.5049 m。

磁定位器选用S32750 级双向不锈钢，该工程弯曲井段工况下弹性模量E1=200 GPa，射孔枪选用P110 级钢，弹性模量E2=207 GPa，桥塞材料选用铸铁，弹性模量E3=170 GPa。

为保证射孔枪设备安全，l2段可承受最大荷载为20 kN，l1，l2段可看作实心圆柱，l3段为内径53 mm，外径97 mm 的空心圆柱，其惯性矩分别为：I1=1.39×10-6m4，I2=3.08×10-6m4，I3=4.35×10-6m4。

将数值代入式（9）～（19）计算可得最大挠度表达式，并计算关于l2的弯曲变形工具串最大可通过长度Lω表达式，又因Lω=l1+l2+l3，所以最后得到以l2为未知数的一元一次方程，求解可得：

最大挠度为0.04261 m，最大挠度位置在距工具串缆线端2.412 m 处。

根据计算可知，该井可下入泵送桥塞工具串的射孔枪段最大长度为2.2683 m。选用射孔枪长1.5 m，点火装置0.5 m，因此最多可携带一级射孔枪。该井发生卡阻事故，且尝试多种方法解卡均失败，究其原因是该井弯曲井段狗腿度过大，下放的工具串超出了可通过的最大长度，导致泵送事故发生。

2.2 数值模拟

基于上述理论分析结果进行数值模拟，对该案例中工具串与管壁接触点以及通过性进行分析验证。井段模型采用长均为6 m 的直-弯-直三段井构成，弯曲井段狗腿度为17.79°/30 m，曲率半径R=96.62 m，入口为流量入口，泵送排量为1.6 m³/min，工具串模型采用三段式，数据如表2 所示。

表2 数值模拟几何数据Table 2 Geometry data for numerical simulation m

理论计算结果表明工具串刚性可通过最大长度为Lmax=4.5049，选用长为5.35、4.49、3.66 m 的工具串模型进行工具串通过性模拟。

如图6 所示，第一组在进入井段后泵送遇阻，工具串卡在弯曲井段。工具串停止前进，动能消失，应力稳定之后观察云图，在管壁上工具串前端、后端和中部最对应的位置有应力分布，接触点为第一类接触点。前端受力比后端大，是因为前端所分担的工具串自重要更大；中部的受力面积明显要大于前端和后端，是因为工具串射孔枪部分与管壁接触在一起，而前后端为端部与管壁接触。

图6 泵送遇阻接触点Fig.6 Contact point of pumping obstruction

图7 为模型沿井眼轨迹方向的速度与时间的曲线，曲线所围面积为模型沿井眼轨迹的路程，如图所示第二、三组模型在经过t2、t3点后速度保持不变，且经过相同路程后速度归零，t2、t3点即位弯曲段与直井段的交界处所在节点；第二、三组模型在t2、t3与0点之间曲线所围面积相等，为第一段直井段与弯曲井段长度之和，且明显大于第一组模型总路程，因此第一组模型曲线所围面积，即位泵送遇阻位置。

第二组模型在弯曲井段速度低于第三组模型的原因是，该组模型长度接近可通过最大长度，观察泵送过程中管壁应力云图可知，管壁受力要明显大于第三组。阻力过大导致速度降低，同时由于速度降低，泵送流体对工具串的轴向推动力与粘滞阻力增大［14-15］。

2.3 影响因素分析

对于某一水平井泵送桥塞工具串可通过最大长度影响因素有多种［16］，包括该井弯曲段最大狗腿度［17］，弯曲段井筒内径等，先将基于上述长度计算公式，工具串可通过最大长度影响因素进行分析［18-20］。

如图8 所示，分别对井筒直径为0.108、0.118、0.128 m 的三组案例进行可通过最大工具串长度与狗腿度的影响因素分析，狗腿度取1～20（°）/30 m，数据间隔为0.1 m，共190×3 组数据。根据图8 可得，工具串可通过最大长度与狗腿度近似成反比，当狗腿度近似为0，即为直井段时，可通过最大长度可趋于无限长。

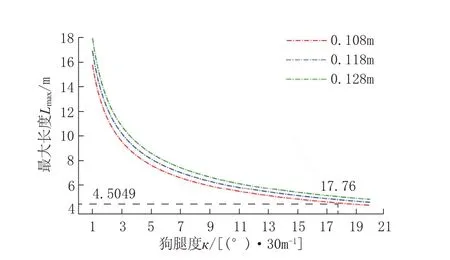
图8 狗腿度对可通过工具串最大长度影响Fig.8 Effect of dogleg severity on the maximum allowable length of the tool string

在套管内径一定的情况下，狗腿度＜5°/30 m时，狗腿度对可通过工具串长度影响显著，狗腿度每增加1°/30 m，可通过工具串长度减少1 m。当狗腿度＞5°/30 m 时，狗腿度每增加1°/30 m，可通过工具串长度减少0.26 m。

因此在施工中应保证钻井质量，尽量避免狗腿度过大的井段出现，即使只有部分井段出现狗腿度过大，但也会造成泵送遇阻。

由图5 可知根据三组不同井筒直径得出三条不同曲线可知，井筒直径越大，可通过最大长度越长。针对井筒直径对可通过最大长度影响，取狗腿度为6、8、10（°）/30 m，分别对井筒直径在0.1～0.13 m 的弯曲井段进行工具串可通过最大长度计算，数据间隔取0.002 m，结果如图9 所示。由该图可知，泵送桥塞工具串可通过最大长度与井筒直径近似成正比，影响系数接近1 m/0.02 m。因此施工中应选取合适的套管尺寸以及工具串尺寸。

图9 井筒内径对可通过工具串最大长度影响Fig.9 Effect of wellbore diameter on the maximum allowable length of the tool string

对比图9 各组数据可以看出，最大狗腿度对最大长度的影响更为显著，为主要影响因素。狗腿度每改变1°/30 m 对最大长度的影响与内径改变0.07 m 等效。

3 结论

本文提出了一种泵送桥塞工具串可通过性判别方法，并针对工程实例进行理论验证与数值模拟分析，而后进行泵送影响因素探讨。基于上述分析，可得到以下结论：

（1）最大狗腿度比井筒内径的影响更为显著，为主要影响因素；

（2）工具串材料的弯曲性能对其通过性影响显著；

（3）桥塞工具串可通过最大长度与该井最大狗腿度成近似反比，在狗腿度＜5°/30 m 时，可通过长度的减少为1 m/［（°）·30 m-1］，＞5°/30 m 时，可通过长度的减少为0.26 m/［（°）·30 m-1］；

（4）套筒内径对可通最大长度正相关，影响率接近1 m/0.07 m。