海上风电场四圆柱基础冲刷问题数值模拟研究

俞梅欣，杨皓然，朱艳，李小军，韩兆龙

（1.中船第九设计研究院工程有限公司，上海 200063；2.上海海洋工程和船厂水工特种工程技术研究中心，上海 200063；3.上海交通大学，上海 200240）

0 引言

近海和深远海中的固定式海洋构筑物的基础结构形式多样，包括重力式、桩基式、导管架式、负压筒式及其他各种新型结构，功能用于海洋能开发、海底监测、深海采矿等，其中在水深不大时，以纯桩基式及导管架结合桩基式结构较为常见，目前已被广泛应用于海上风电机组及海上升压站基础结构等海洋构筑物的建设中。但在海洋环境下，基础底部局部冲刷现象经常发生，引起桩柱失稳和局部强度下降等问题，甚至会影响整个风电基础的稳定性。海流作用下单桩与桩群的冲刷问题引起了学术界和工程界的关注，采用理论分析、物理试验与数值计算研究方法开展了一系列研究工作，并取得了相关成果[1]。

截止目前，单桩冲刷问题的研究已有较多报道。Roulund 等[2]采用数值计算与物理试验相结合的方法开展了单桩冲刷问题的研究，分析了雷诺数、粗糙度与边界层厚度对桩后泥沙运动的影响。祁一鸣等[3]研究了洋口海域环境作用下的海上风电桩基局部冲刷问题，提出了防护措施以保证风力机的稳定性。

此外，随着高性能计算技术的进步，一些学者采用数值计算方法对冲刷问题中的流场演化、泥沙运动与结构稳定性等方面进行研究[4]。漆文刚等[5]发现冲刷引起的桩基埋深变化会改变桩基的受力模式。Nagel 等[6]采用两相流模型对单桩冲刷问题进行了研究，分析了桩基周围流场分布对泥沙输运的影响。Song 等[7]采用浸入边界方法研究了单桩周围泥沙运动规律。骆光杰等[8]采用FLOW 3D软件建立三维计算模型，对比研究了不同尺寸圆形挡板工况下单桩基础局部冲刷防护效果。

相对于单桩工况而言，多桩冲刷的工况更为复杂，逐渐引起重视。Liang 等[9]对3 种不同布置形式下单桩、多桩的冲刷问题进行了试验研究，对冲刷深度进行了对比分析，并提出了简化计算公式。邹东波[10]采用数值计算与物理试验相结合的方法，对单桩与圆形八桩群的抗冲刷性能进行研究，得到了冲刷深度随时间变化的计算公式，同时提出了新型的防冲刷装置能减轻60%的作用。及春宁团队采用数值模拟方法对单桩、双桩与圆形八桩群的局部冲刷问题进行了研究，分析了水深与桩间距对冲刷的影响，并阐明了桩群局部冲刷的流动机理[11-12]。

海上风电机组的导管架基础结构底部在海床面处多为正方形排列四圆柱基础支撑，目前，对四圆柱桩群基础局部冲刷问题的研究还不成熟。因此，本文主要研究不同来流方向对正方形布置四圆柱群基础的流场分布和局部冲刷的影响。

1 计算模型

1.1 计算参数

本次研究项目背景为某海域的海上风电工程项目，其主体基础形式为导管架基础结构，导管架底部为正方形排列的四圆柱桩基支撑。其计算模型图见图1。正方形边长处2 个圆柱圆心的距离为15 m，桩的直径D=2.2 m，计算水深14.7 m，表层水流来流流速2.5 m/s，切向流速分布采用二维模型试算求得。水底面往下7.3 m 深度为淤泥土，底质泥沙中值粒径0.1 mm，泥沙密度2 650 kg/m3。具体的工程参数见表1。通过数值模拟方法研究四圆柱基础的冲刷问题。

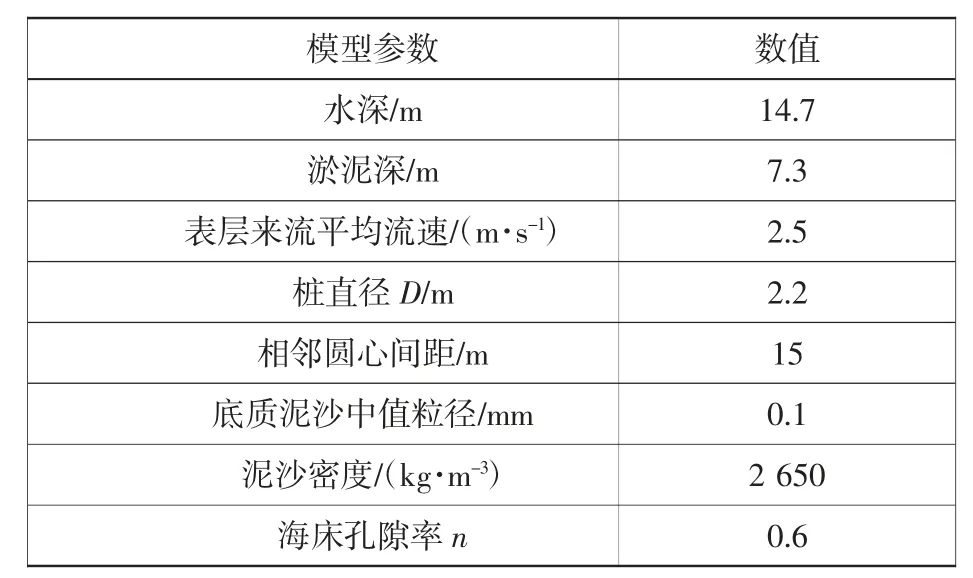
表1 四圆柱基础冲刷问题的工程参数Table 1 Engineering parameters for the scour problem of a four-cylinder foundation

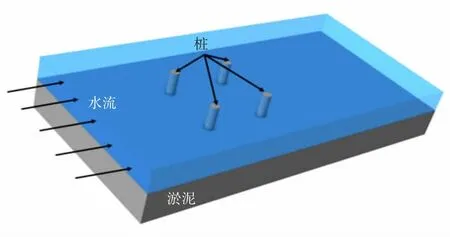
图1 四圆柱基础冲刷模型示意图Fig.1 Schematic diagram of four-cylinder foundation scour model

1.2 控制方程

计算模型中，流体的控制方程采用连续性方程和Navier-Stokes 方程描述[7，12]。由于该问题涉及到湍流计算[7]，采用SSTk-ω 湍流模型描述水流动力学问题（式（1）、式（2））。

式中：k和ω 分别代表湍动能和单位湍流动能耗散率；Pk为湍动能生成率，Pk=υt S2；Cμ、β 为经验常数，本文中Cμ=0.09，β=0.082 8；S是流体应变率张量的标量不变量，其中Sij=0.5（U+为流体的应变率张量，U为速度矢量，包含x，y，z方向的速度分量；F1为混合函数，在边界层内层大部分区域上等于1。

对于水底的水-泥沙界面的床面高程的控制方程用Exner 方程表达（式（3））。

式中：zb为局部床面高程；n为沙床的孔隙率；qB为海床面的泥沙输运率。

海床面泥沙输运率方程采用经验公式计算（式（4）），其中θ=｜τ｜/（ρɡRd）是泥沙的希尔兹数，θc是泥沙的临界希尔兹数。

数值计算在OpenFOAM 开源平台和64 核小型服务器上进行。流体计算采用pisoFoam 求解器，采用了有限体积法求解式（1）中的湍流模型。流体域和泥沙域采用浸入边界法开展耦合计算。具体其他参数物理意义和计算过程，参见参考文献[7]。

图2 为流体域和淤泥泥沙域的计算网格模型，整体计算域尺寸为宽×长×深=20D×40D×10D（D=2.2 m），其中水深∶淤泥深=2∶1。考虑2 种来流角度α=0°和α=45°，分别对应图2（a）和图2（b），总的计算网格数分别是2 389 804 和2 351 862。通过多次试算，取计算时间步长Δt=0.001 s。时间步长过大会造成计算发散，步长过小会加大计算量。

图2 不同来流入射角的四圆柱冲刷问题的计算域和网格Fig.2 Computational domain and grid for four-cylinder scouring problems with different incidence angles of flow

2 算例验证

为验证本文数值方法的可靠性和适用性，采用单圆柱型桩冲刷算例开展验证比较研究。该算例中，圆柱的直径D=53.6 cm，水流来流流速0.46 m/s，底质泥沙中值粒径0.26 mm，泥沙密度2 650 kg/m3。图3（a）为该算例的计算域，尺寸为宽×长×深=9D×14D×4D，总计算深度0.4 m，其中水深∶淤泥深=1∶3。计算总网格数453 024，计算时间步长Δt=0.001 s。数值计算方法同前，验证算例的工程参数如表2 所示。

表2 验证算例的工程参数Table 2 Engineering parameters for the verification example

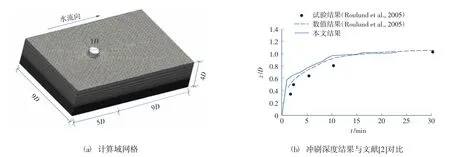
图3 单圆柱冲刷验证算例Fig.3 Verification calculation example of single cylinder scour

图3 （b）为本文单圆柱冲刷深度的数值结果与Roulund 等[2]的数值模拟和试验测量的结果对比图。可以看到，本文的数值模拟结果与文献的结果接近，平稳后的单桩冲刷深度为1D左右。该结果验证了本文使用数值方法研究圆柱冲刷问题的可靠性和适用性。

3 结果和讨论

图4 为来流垂直方向平均流速分布图，流速分布呈现出明显的抛物特性，近海床区域流速几乎为0，离开海床后流速快速增加并接近表层来流速度。

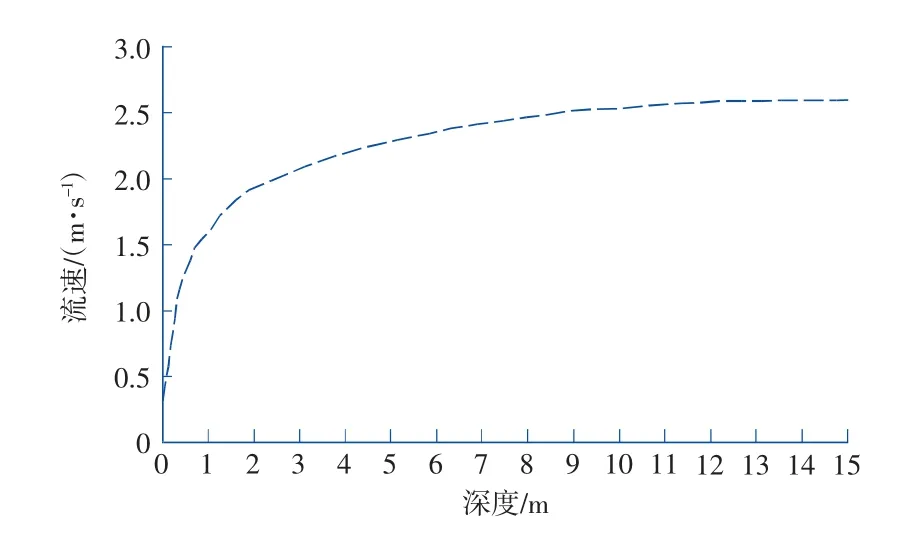
图4 垂直方向的平均流速分布Fig.4 Average velocity distribution in the vertical direction

图5 、图6 分别为来流α=0°和α=45°的情况下，四圆柱的x方向速度场及涡量场分布图。可以清楚地看出，由于圆柱的存在和边界条件的变化，在圆柱周围发生剧烈的流场速度变化和涡脱落现象，同时上游圆柱会产生涡脱落，撞击在下游圆柱周围，在下游圆柱进一步产生新的涡脱落，这些涡旋向远尾流区进一步发展。

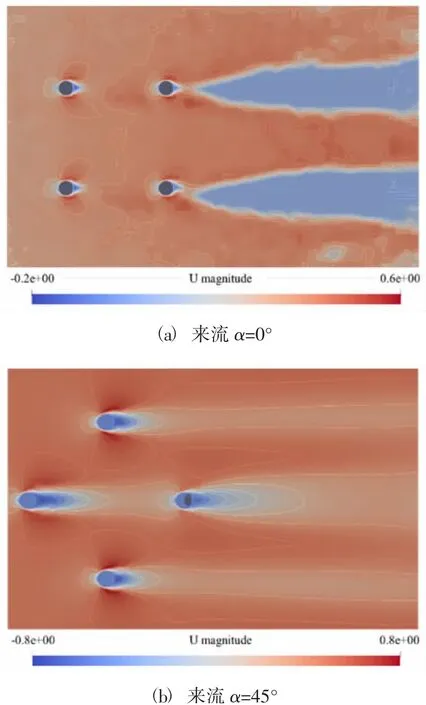
图5 x 方向的平均速度场Fig.5 Averaged velocity field in the x-direction

图6 x 方向的瞬时涡量场Fig.6 Instantaneous vorticity field in the x-direction

图7 为冲刷引起的海床表面的三维变化图，图7（a）和（b）分别为对应来流角度α=0°和α=45°的情况。

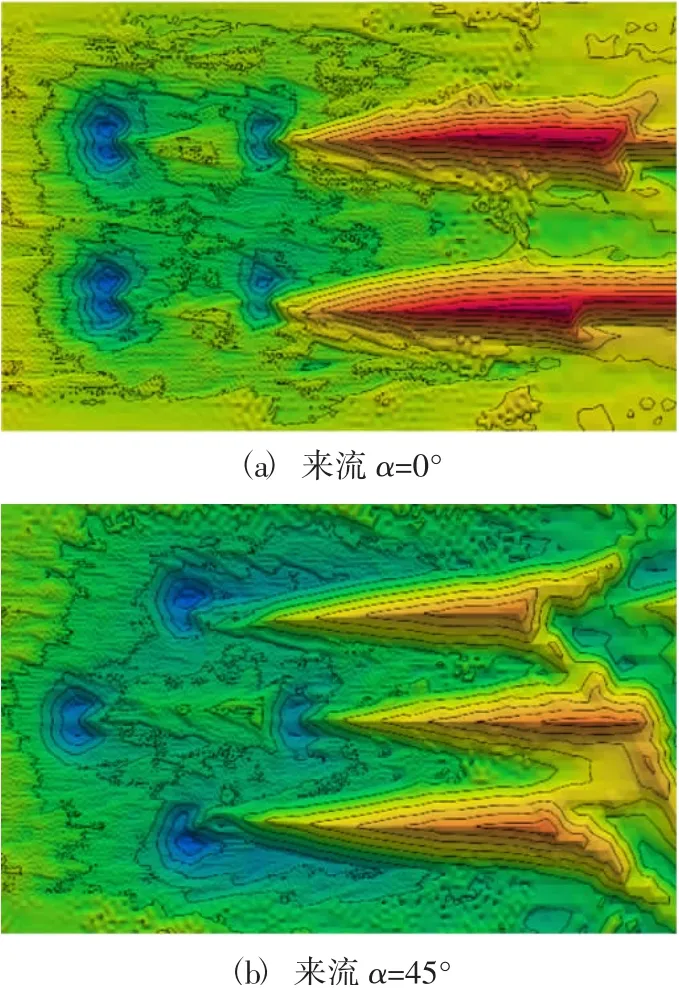
图7 不同角度来流下冲刷引起的海床表面冲刷形态Fig.7 The scour pattern on the seabed surface caused by scour from different angles of flow

为清楚显示冲刷结果，四圆柱基础设置为隐藏状态。可以看出，速度剧烈变化和涡旋撞击是产生冲刷的重要原因，在速度变化剧烈和涡旋冲击频繁的地方，如圆柱底部周围和下游区，产生了很明显的冲刷坑和地形变化，在圆柱基础底部产生较大的冲刷深度。对比（a）和（b）图，由于来流的不同角度，冲刷产生的地形变化也有所不同。来流角度α=45°时侧向的两桩在尾流干扰作用下出现了明显的冲刷形态不对称，而来流角度α=0°时冲刷形态几乎对称分布。经测量，（a）和（b）中的最大冲刷深度约为2.5 m（≈1.14D）和2.6 m（≈1.18D），（a）中最大冲刷深度出现在上游两桩处，（b）中最大冲刷深度出现在侧方两桩处。冲刷深度数值模拟结果与韩海骞公式[13]、美国科罗拉多大学HEC-18公式[14]、Gao 公式[15]的对比见图8。

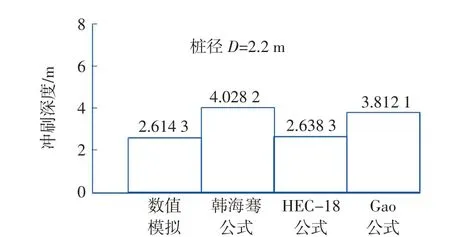
图8 数值模拟与经验公式冲刷深度对比Fig.8 Comparison of scour depth between numerical simulation and empirical formula

可以发现数值模拟计算得到的冲刷深度相对于韩海骞公式和Gao 公式较小，与HEC-18 公式接近。

4 结语

本文采用OpenFOAM 计算平台数值研究了海洋风电正方形排列四圆柱基础的冲刷问题，分别采用SSTk-ω 湍流模型描述水流动力学，采用Exner 方程描述水-泥沙交界面运动，采用浸入边界法描述水和泥沙的耦合作用，研究了来流α=0°和α=45°两种情况，得出相关结论如下：

1） 该数值方法可较好地模拟海洋风电圆柱类型支撑基础的冲刷问题，验证算例显示数值结果与文献试验结果吻合良好。

2） 基础冲刷产生的重要原因是流场的速度变化和涡旋脱落；不同的来流角度会产生不同的流场变化，因此也会引起不同的冲刷地形。

3） 对于四圆柱基础，每个圆柱都产生了不同程度的较大冲刷深度，且在尾流区也会产生冲刷地形的变化。

以上方法和结论可以为研究海洋风电的基础冲刷问题提供参考和支撑。