探究最小二乘配置法在高层建筑物中的应用

曾 致，雷 刚

（西安市勘察测绘院，陕西 西安 710054）

0 引言

随着社会技术的进步和中国现代化进程的不断加快，城市各类高层、超高层建筑越来越普及化和密度化[1]。城市建筑物高度以及承载度的增加，使得地基基础及周边的地层发生形变，建筑物发生不可预估的沉降，如果沉降形变值超过某一限值时，将会严重影响建筑物安全和人民生命安全[2-3]。因此，城市高层建筑物在建设过程中必须对其进行不定周期的沉降监测，以便对建筑物以及周边地质的沉降量及沉降速率进行分析和预测，这也是保障建筑物安全和顺利完工的关键[4-5]。

目前，很多学者针对建筑物的沉降观测展开了多层次的研究。熊俊楠等[6]利用平差模型与基点稳定性的联系对高程建筑物沉降进行了分析；牟洪洲[7]针对GM（1，1）模型、多元回归分析模型及时间序列分析模型，得出组合模型比单一模型在拟合和预测上更具有优势；闫宏亮和马得花[8]对无偏灰色模型、时间序列线性移动平均法及马尔科夫模型进行研究，并在此基础上建立时间序列—马尔科夫组合模型对建筑物沉降进行预测；王海城和徐进军[9]针对构造方法的不严密性，给出了灰导数法背景值构造模型和参数最优估值的计算方法，对南水北调工程沉降监测实例进行建模预测，收到了良好效果；孙策等[10]提出了一种基于小波分解的SVM-AR组合预测模型，得出在小样本、低信噪比条件下具有更好的预测性能，能够对高层建筑物沉降进行准确模拟与预报；徐飞[11]针对高层建筑物沉降预测模型精度低、与实测值不符等问题，提出了基于时序SAR技术的高层建筑物沉降变形预测方法。通过计算，结合BP神经网络构建高层建筑物沉降变形模型，实现沉降变形预测，王洪德和李骞[12]为了对地铁车站深基坑施工过程引起的周边建筑物沉降进行预警，利用改进的灰色Markov模型，预测地铁车站施工过程中周边建筑物的沉降量。研究结果表明：与改进的灰色模型相比，改进的灰色Markov模型预测的相对误差从4.2%降到2.1%，程朋欢和卢德基[13]提出一种使用辛普森公式优化背景值的灰色模型，以新的积分方式优化背景值以提高模型预测精度。通过基坑沉降与地表沉降两组实例进行实验，结果表明，使用辛普森公式优化背景值后，模型的预测精度更高。但是对高层建筑沉降普遍性研究较少。

基于此，文章利用MATLAB对最小二乘配置法、时间序列进行建模，对高层建筑物实测沉降数据建立预测模型，对几期沉降形变进行预测，将预测数据与实测数据进行比对分析，从而探究最小二乘配置法在高层建筑物形变监测数据处理中应用的可行性及适用性，为高层建筑施工提供参考依据。

1 研究方法

1.1 最小二乘配置法

最小二乘配置模型和随机模型为[14-17]：

式中：L为观测向量；Y为非随机参数向量；X为信号；Δ 为观测噪声；X=（X1，X2）T，X1为观测点信号，X2为未测点信号，R（B）=m；R（G）=t，分别为系数矩阵的秩。

误差方程为：

按照最小二乘配置原理估计的准则有：

该公式为最小二乘配置原理，式中P为对称正定方阵，是观测值L的权；R为一个适当给定的正定矩阵，称为正规化矩阵；利用拉格朗日乘数法，构造如下函数：

式中：KT=[K1，K2，...，Kn]，分别令

由此得到法方程为：

由于G，B 列满秩，故可证明法方程系数阵可逆，未知量X̂和Ŷ有唯一解。由法方程可以得到：

式中：M=B（BTPB+R）-1BTP，I为单位矩阵，当R矩阵正定时，就可以得到X̂和Ŷ的唯一解。

通过上述计算可得观测值的估值为：

令

则L̂=J(α)L

在这里称J(α)为帽子矩阵。

其中，

Ŷ的方差阵为

V 的方差为：DV=J(α)DΔJ(α)T

最小二乘配置法的特点：

（1）函数模型中引入了随机参数Y，并且已知了先验期望和方差，这是最小二乘配置最大的特点，因此这种方法的应用前提是必须要求比较准确的已知先验统计特性。

（2）求参数的估值可称为拟合，求已测点信号S为滤波。估计与S 之间存在协方差关系，而与观测无直接关系的未测点信号称为推估。

（3）由于模型中导入了信号，随机量方差不再等于其误差方差，而是误差方差和信号方差合成的一种方差，但其衡量观测精度的指标仍是其误差方差。

1.2 时间序列

按时间顺序排列的一组随机数据称为随机时间序列。在工程建设中，时间序列也得到了广泛应用，时间序列可以预测边坡的位移、建筑地基的沉降量、隧道变形、基坑支撑轴力等。

设有连续观测样本序列{x1，x2，…，xn}，对应的白噪声序列{a1，a2，…，an}，白噪声的序列均值为0，且相互独立。其具有以下优势：

（1）时间序列模型是动态模型，它对动态数据具有外延特性。

（2）时间序列模型能描述随机变量与其他变量之间的相关关系，以及时间序列内部的相关关系。

（3）由于时间序列分析是建立在输出等价的基础之上，可将所观测到的时序作为系统的一维或多维的输出。变形体位移构成时序，从统计角度来揭示各时序内部与各时序之间的统计关系。

2 高层建筑物沉降量预测

2.1 沉降观测点分布情况

本工程以某29层高的建筑物为研究对象，现场沉降观测点分布情况如图1所示。监测网由逆时针方向布设在墙体上的15个监测点组成，点间距分布均匀，形变监测点埋于室内地面上方20～40 cm处。

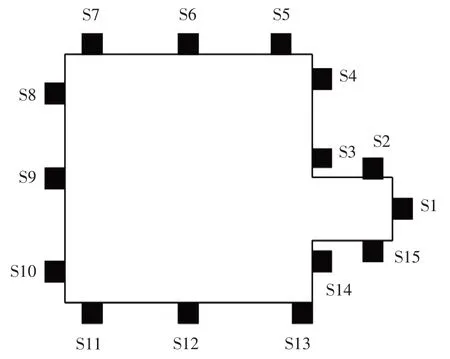
图1 沉降观测点分布图

为确保观测成果可靠性和正确性，监测网数据处理分析采用采用已知的控制点进行联测，利用几何水准测量的方法进行现场观测，观测精度符合二等水准测量规范要求。通过检核，在观测中最大沉降量为7.2 mm，最小沉降量为0.8 mm，累计沉降量为42.8 mm，平均沉降量4.12 mm＜200 mm，未出现沉降异常变化，所有观测结果均符合《建筑地基基础设计规范》《建筑形变测量规范》《建筑物沉降观测方法》等[18]国家规范中高层建筑物沉降的要求。

2.2 沉降数据获取与处理

文章以S1为模型计算点，沉降观测时间选取为2022 年3 月15 日—2022 年9 月28 日，共获得30 期沉降数据，其中1～21 期为实测数据，22～30 期为预测数据。对所获的1～21 期实测数据利用MATLAB软件，用最小二乘配置法对时间序列进行建模以及平差解算，获得22～30期的预测沉降高程及精度，为后文的沉降分析及变形异常提供数据基础。实测高程与预测高程相关数据详见表1、表2。

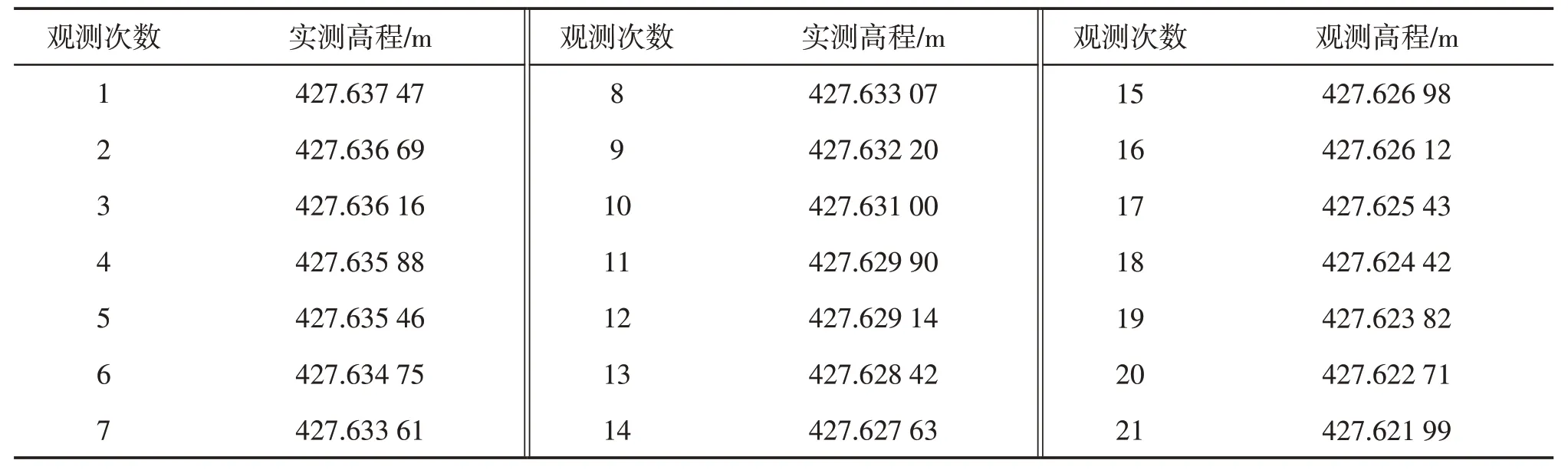
表1 S1点观测次数与实测高程值

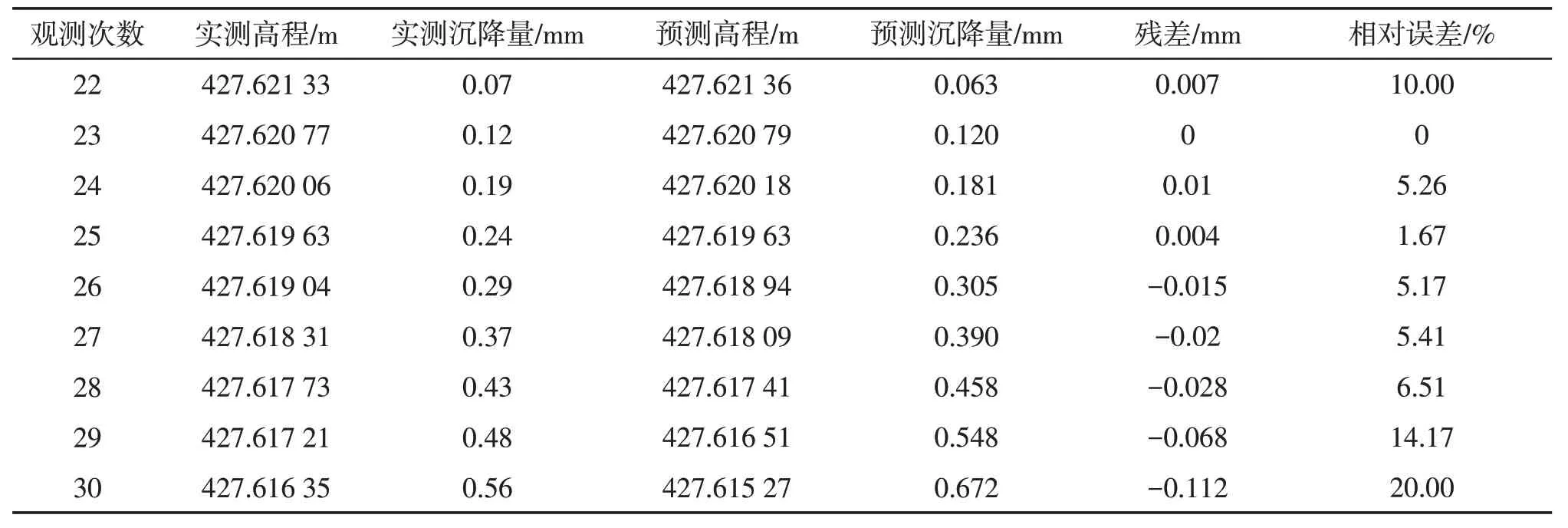
表2 实测高程与预测高程

由表2分析可知，残差绝对值介于0～0.112 mm，相对误差最小为0，最大为20%，平均相对误差为3.81%。其中，随着预测期数增加，实测沉降量与预测沉降量差值越来越大，从28期开始残差绝对值和相对误差呈倍数增加，说明了最小二乘配置在高层建筑物沉降量适合短期预测，而长期预测与实测数据还是存在一定的差距，并且随着时间的增加而增加。同时，从图2可看出，预测数据和实测数据相对沉降趋势呈一致性变化，表明了该建筑物地基的稳定性。

图2 实测高程和预测高程变化趋势

从表3 和图3 分析可得出，预测沉降变化趋势与实测沉降变化趋势基本保持一致，但由于未能考虑沉降监测存在的外部误差，导致部分点位变化异常，这对整体预测趋势精度有所降低。

表3 实测高程与预测高程沉降量

图3 实测高程与预测高程沉降趋势变化

综上所述，最小二乘配置法适合对短期沉降进行预测，而对于高精度、观测时间长的建筑物，不适合定量预测，只能从沉降量趋势变化分析建筑物沉降。同时，下一步将最小二乘配置法与小波变换、灰色预测模型结合，处理观测数据噪声后预测沉降变化。

3 结论

基于MATLAB 对最小二乘配置法及时间序列对高层建筑物实测沉降数据建立预测模型，对几期沉降形变进行预测，将预测数据与实测数据进行比对分析，从而探究最小二乘配置法在高层建筑物形变监测数据处理中应用的可行性及适用性。

（1）从预测数据和实测数据对比分析可知，最小二乘配置法方法简单、预测精度高，在高层建筑物沉降中适合进行短期预测，但长期预测与实测数据还存在一定的差距，残差绝对值和相对误差呈倍数增加。

（2）从沉降趋势变化可知，最小二乘配置法在沉降趋势变化中具有优势性，并对部分点位异常变化能够及时反应，这为判断沉降量是否出现异常提供了参考。

（3）该方法未能对观测数据噪声进行去除，使预测数据精度有所降低。下一步将最小二乘配置法与小波变换、灰色预测模型结合，对高层建筑物进行预测分析。

（4）将最小二乘配置法与时间序列组合，同时利用MATLAB 优势，对最小二乘配置法进行了改进和程序化，提高了对大型建筑物变形数据的处理能力，缩短了变形监测的周期，便于对某一建筑进行动态监测。