风对孤立波海堤越浪特性影响的数值模拟研究
张良斌,屈 科*,2,3,黄竞萱,王 旭,虢 磊
(1.长沙理工大学 水利与环境工程学院,湖南 长沙 410114; 2.洞庭湖水环境治理与生态修复湖南省重点实验室,湖南 长沙 410114; 3.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114)
0 引言
海啸通常由海底地震、火山爆发、海底滑坡或极端气候变化等引起[1-3]。当海啸从远海传播至近岸时,受海底地形变化、水深变浅以及海岸建筑物等的影响,波浪产生变形,波高迅速增大,在海堤附近会发生越浪现象。当越浪量超过一定极值时,会对沿海城镇的基础设施和人民的生命安全造成严重威胁,如2004年的印度尼西亚海啸和2011年的东日本海啸产生的影响[4-7]。有学者认为孤立波与海啸有着相似的波形和水动力特性[8-9],因此近些年常用于模拟研究海啸等类似浅水大波与海岸工程建筑物之间的相互作用。
设计海堤时,一般采用物理模型实验或基于物理模型实验的经验公式来计算越浪量。1992年DE WAAL 等[10]对斜坡式海堤的越浪开展了物理模型实验的研究,提出了单斜坡的平均越浪量及最大越浪量的计算公式,并对岸滩坡度、水深以及堤顶超高等影响波浪爬高和越浪的因素进行了系统分析。HUNT[11]通过物理模型实验系统研究了波群、聚焦波以及孤立波作用下海堤的越浪特性,分析了入射波高与单宽越浪量之间的关系。随着计算机技术的发展,数值模拟计算方法被逐渐运用到波浪与海岸建筑物的相互作用中。HSIAO 等[12]和LIN 等[13]根据孤立波在海堤上越浪过程的三种基本形态,开展了一系列物理模型实验和数值计算,对孤立波的传播演变过程、海堤受力状况、越浪量以及最大爬高进行了系统性的测量与分析。张金牛 等[14]通过数值波浪水槽系统研究了孤立波在斜坡式海堤上越浪的水动力特性,分析了相对波高、相对超高等对越浪量的影响。曾婧扬 等[15]采用两相流模型对斜坡式海堤的越浪特性进行了研究,分析了堤顶超高和相对波高对越浪量的影响,给出了越浪流厚度和最大流速的分布形式和经验公式。王键 等[16]通过模拟不同断面尺寸带胸墙的斜坡堤越浪,分析了不同斜坡堤相关因素对平均越浪量的影响。万德成 等[17-18]采用流体体积函数法 (volume of fluid, VOF)对孤立波越过潜堤和直立柱的黏性流动进行了数值模拟。学者还通过数值模拟分析了向岸风对孤立波在不同建筑物上传播演变的影响,如海岸桥梁、不透水人工岛礁等,研究结果发现,向岸风对孤立波的传播变形、破碎有显著影响,会增大波浪冲击建筑物的水动力荷载[19-21]。总体而言,目前对向岸风作用下孤立波在海堤上的越浪水动力过程的研究比较少。本文基于二维不可压缩两相流数值模型,系统研究了向岸风风速、入射波高、堤顶超高、岸滩坡度以及海堤坡度等因素对孤立波在斜坡式海堤上越浪水动力特性的影响,以期对海岸工程的防护提供参考。
1 控制方程和数值方法
1.1 控制方程
基于两相流数值模型,液体和空气均被认为是不可压缩的,流体的黏滞系数假定为常数,向岸风作用下孤立波与海堤之间的相互作用可用连续性方程和动量方程[22]进行表示:
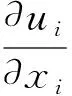
(1)

(2)
式中:ui和uj表示笛卡尔坐标系下的速度分量(i、j=1、2,分别表示二维流体运动的水平和垂直两个方向);xi和xj表示笛卡尔坐标系下的坐标分量;t表示时间;p表示静压;ρ表示混合流体密度,ρref表示参考密度;μl表示层流动力黏度,μt表示湍流动力黏度,有效动力黏度μeff=μl+μt;gi表示垂直方向上的重力加速度,取9.81 m·s-1。
1.2 数值方法
采用非结构化网格单元上的有限体积法对公式(1)和(2)进行离散。采用压力隐式算法(pressure implicit with splitting of operators, PISO)对压力和速度进行耦合求解[23]。采用一阶迎风格式和二阶伽马格式的加权组合方法对对流项进行离散[24-25]。为保证计算的精度和稳定性,采用动量平衡插值法[26]对控制单元从中心到表面进行速度插值,并利用二阶中心差分法对压力梯度项和扩散项进行离散。
采用WILOCX[27]的经典两方程中的k-ω湍流模型确定湍流动力黏度μt,并通过求解以下湍流运输方程得到湍动能k和湍流耗散率ω:
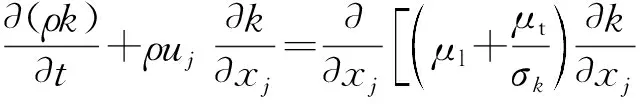
(3)
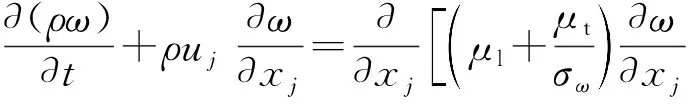
(4)
式中:cμ、cω1、cω2、σω和σk为常数,cμ=0.09,cω1=5/9,cω2=5/6,σω=σk=2;S表示流体的应变率张量,|S| 表示其数值的大小:
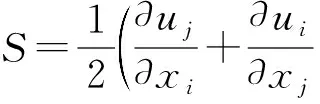
(5)
采用VOF方法捕捉水和空气的交界面,控制方程如下:
(6)
式中:γ表示网格单元中的水相体积分数,不同的水相体积分数值代表不同的含义。γ=1表示流体单元,γ=0表示空气单元,0<γ<1表示水和空气的混合单元。
计算域中,控制单元内的混合流体密度和层流动力黏度可用以下公式进行计算:
ρ=ρair+γ·(ρwater-ρair)
(7)
μl=μair+γ·(μwater-μair)
(8)
式中:ρair和ρwater分别表示空气和水的密度,μair和μwater分别表示空气和水的动力黏度。
2 数值模型验证
2.1 孤立波在斜坡式海堤上的越浪量验证
为验证数值模型计算孤立波在斜坡式海堤上越浪水动力过程的准确性,将数值计算结果与HUNT[11]的实验数据进行对比。实验区域布置如图1所示。模型水槽长36.000 m,宽27.000 m,高3.000 m,斜坡布置在距离造波区8.330 m处,海堤布置在距离斜坡坡脚8.125 m处,海堤两侧的坡度为1∶2,海堤的堤顶宽度为0.215 m,海堤的堤顶高度为0.617 m。实验中入射波高H为0.10 m,静止水深h为0.50 m,实验采用5个浪高仪(WG1~WG5)来测量孤立波在斜坡式海堤上的传播变形过程。进行数值模拟计算时,为验证网格无关性,采用三套不同分辨率的网格进行计算。数值模拟的孤立波波高时程曲线与实验数据的对比如图2所示,个别测点与实验数据有些许差异,可能是数值模型网格划分带来的离散误差所致,但总体上孤立波的波峰和波形与实验结果吻合较好。图3表示不同时刻的沿程水位高程的空间分布,通过对比发现,数值模拟的水位高程的沿程空间分布与实验结果吻合较好。孤立波的时程越浪量变化如图4所示,数值模型很好地模拟了孤立波在海堤上的越浪水动力过程。
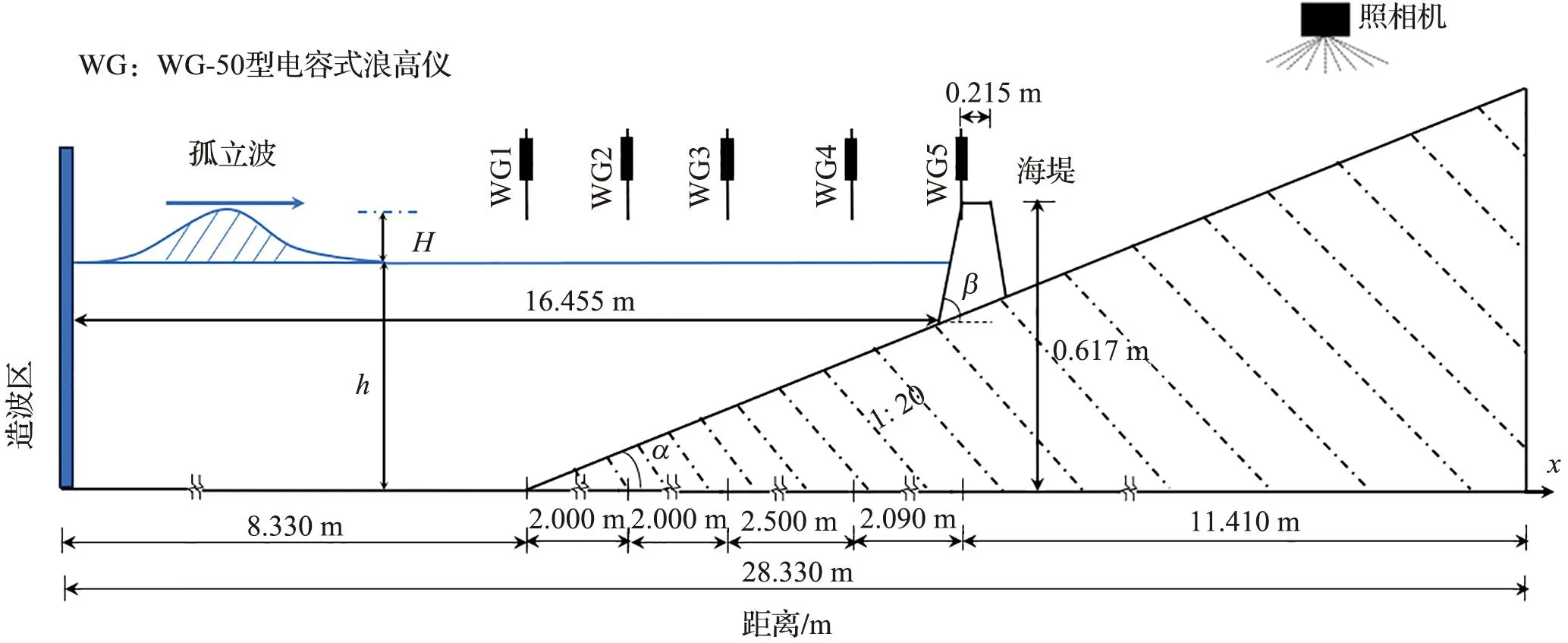
图1 实验区域布置图[11]Fig.1 Experimental layout[11]
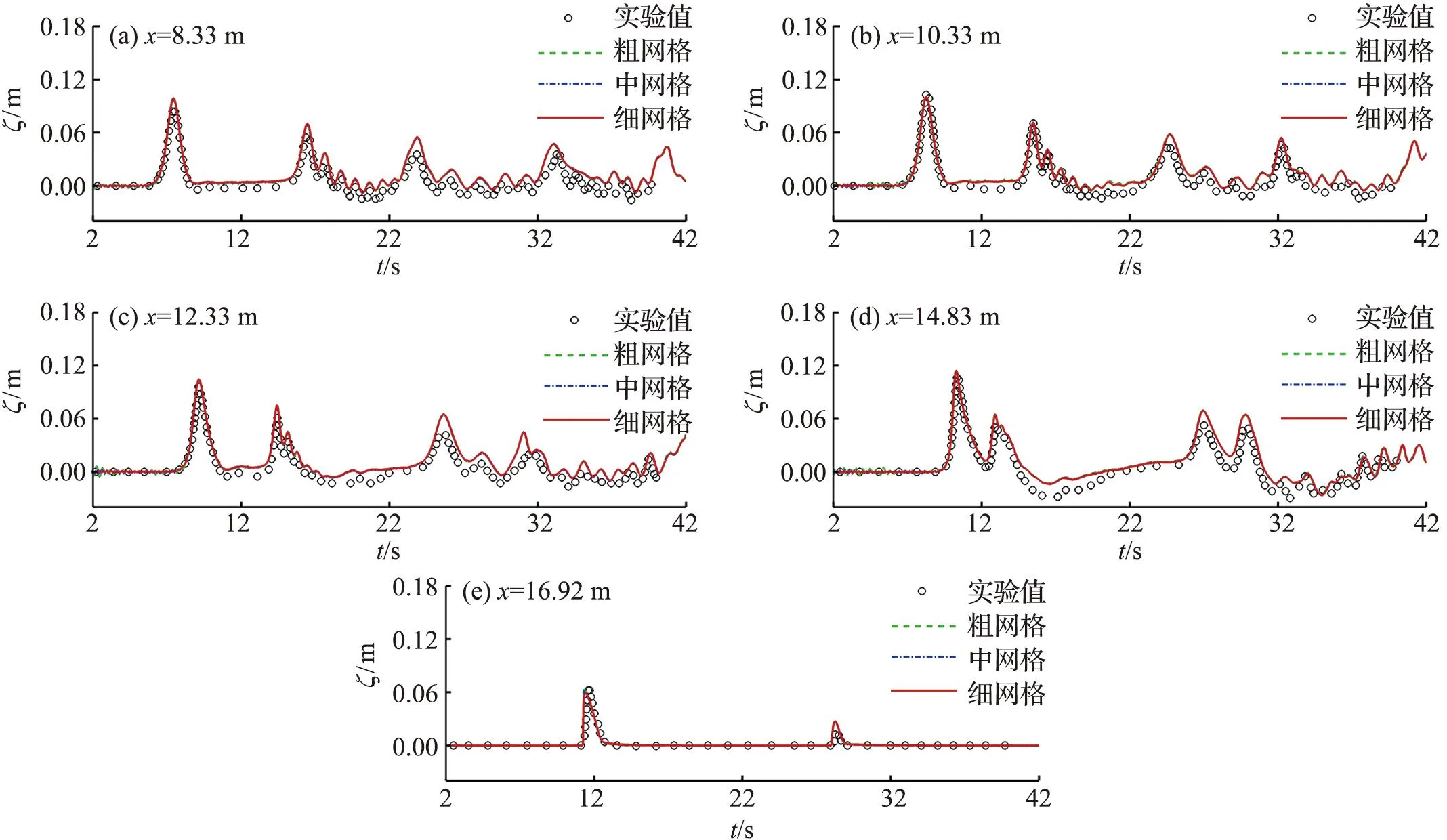
图2 不同测点处的波高时程曲线Fig.2 The temporal evolution of wave height for different wave gauges

图3 不同时刻的沿程水位高程空间分布Fig.3 Spatial distributions of wave elevation at different times
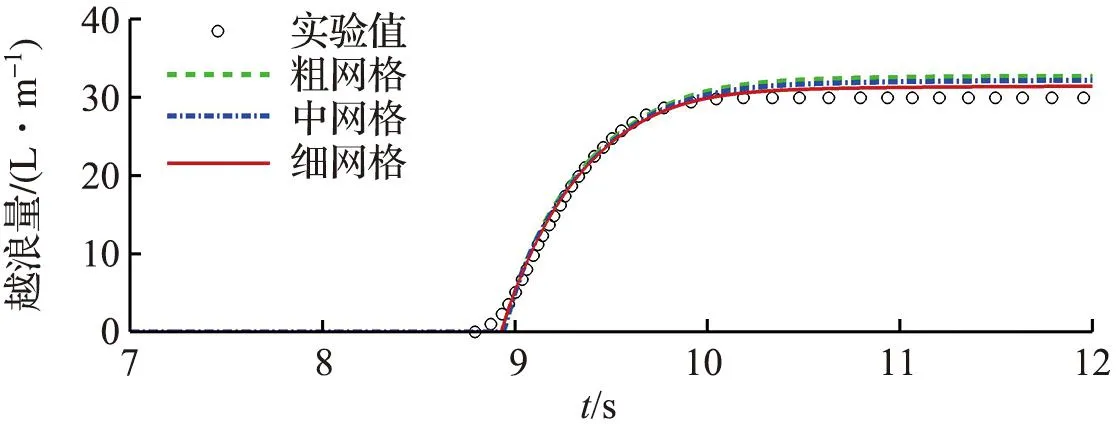
图4 孤立波的时程越浪量Fig.4 The temporal evolution of solitary wave overtopping volume
2.2 风影响下规则波传播变形的验证
为验证数值模型计算风对波浪传播变形的准确性,与JIANG 等[28]的物理模型实验结果进行对比(图5)。模型水槽长45.000 m,宽0.800 m,高1.000 m,斜坡坡度为 1∶10,距造波边界13.250 m。每间隔0.600 m布设一个测点,共布设7个测点,第一个测点布设在坡脚处。实验中规则波的波高H为0.07 m,入射波周期T为1.5 s,静止水深h为0.40 m,恒定风速Uw为5.0 m·s-1。不同测点处数值模拟的波高时程曲线与实验数据的对比结果(图6)显示,数值计算结果与实验数据吻合较好,该数值模型可用于计算风对波浪传播变形的影响。
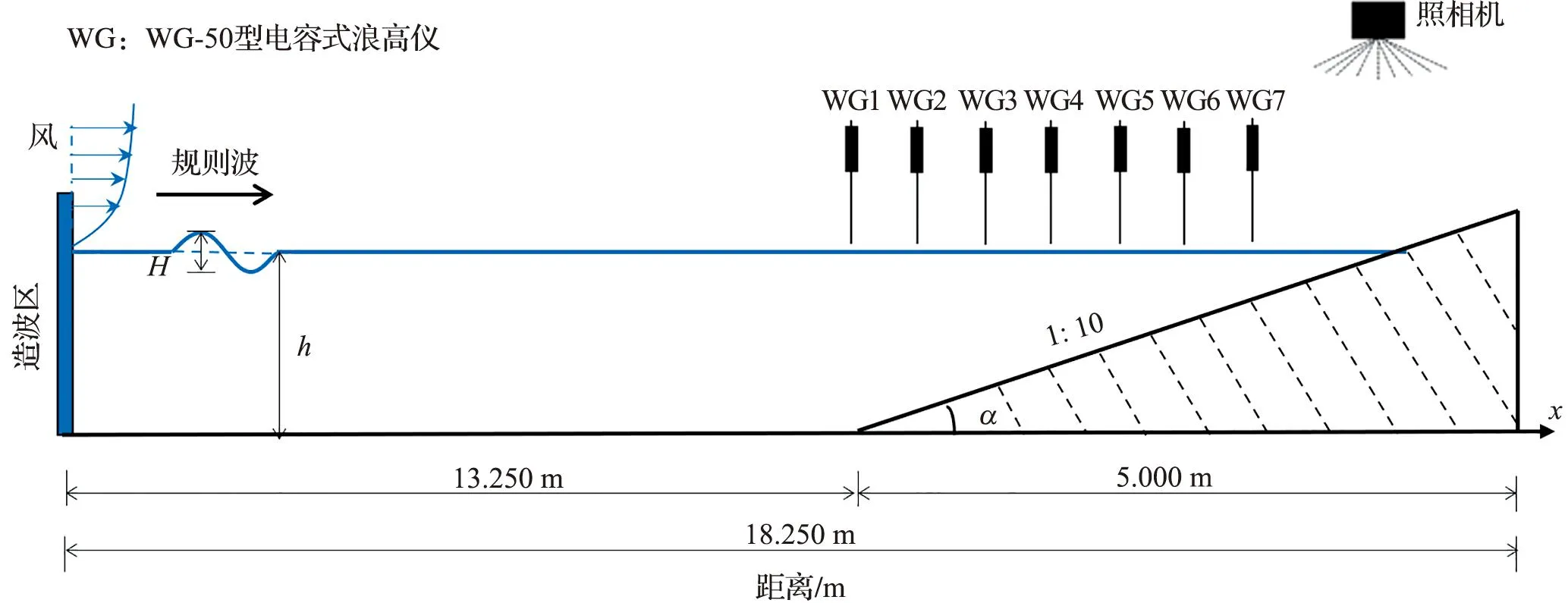
图5 实验区域布置图[28]Fig.5 Experimental layout[28]
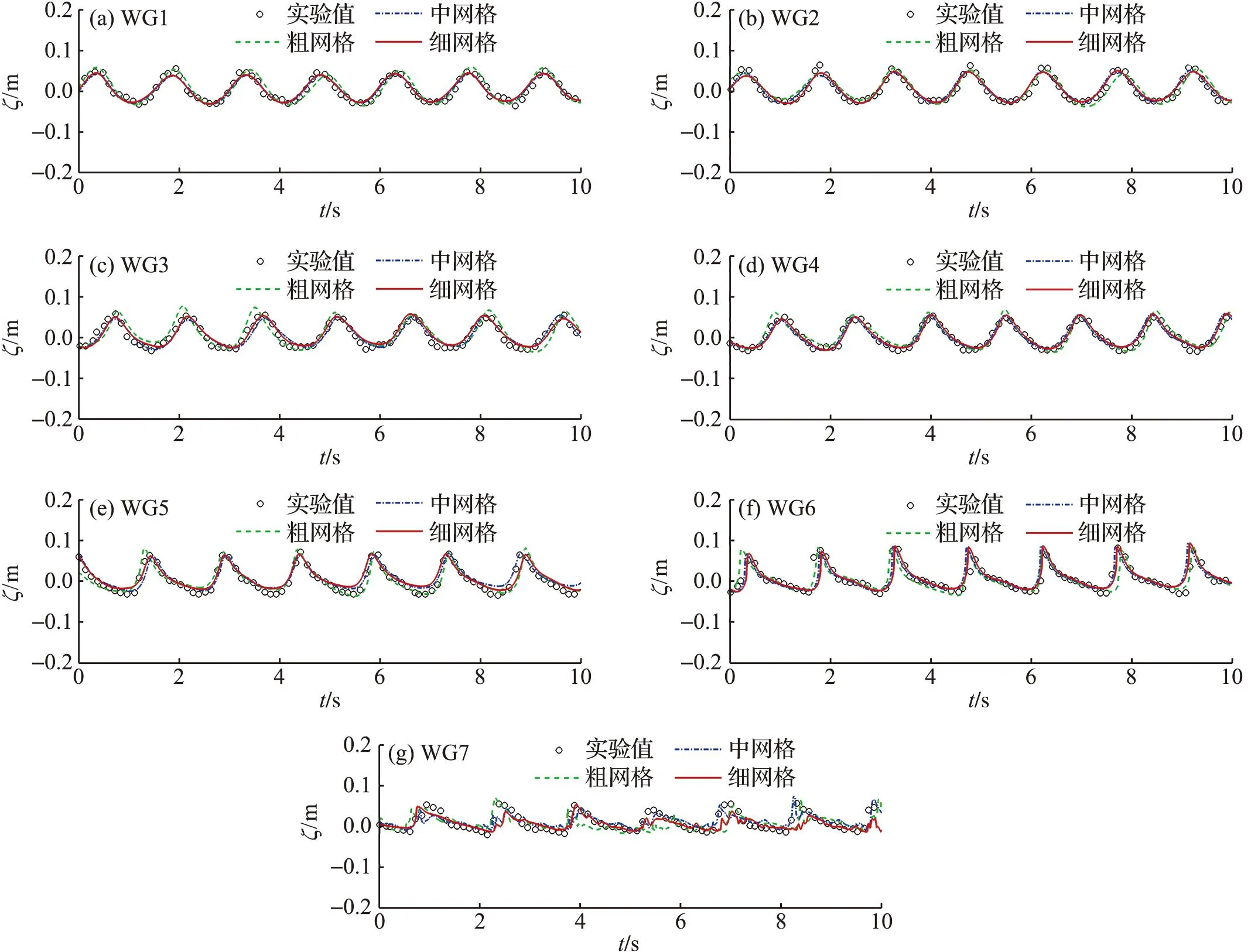
图6 不同测点处的波高时程曲线Fig.6 The temporal evolution of wave height for different wave gauges
3 工况设置与结果分析
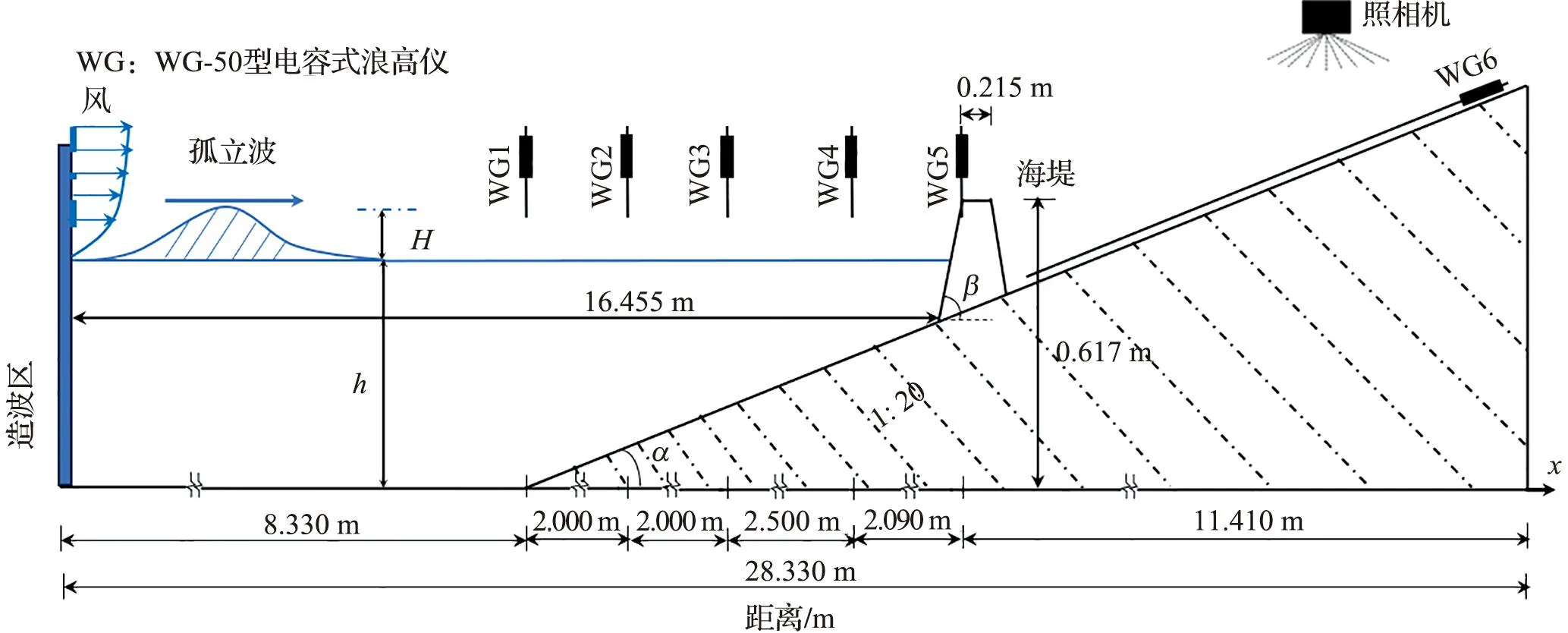
图7 计算区域布置图Fig.7 Computational layout
(9)
当S0<0.025时,表示为激破波;当0.025
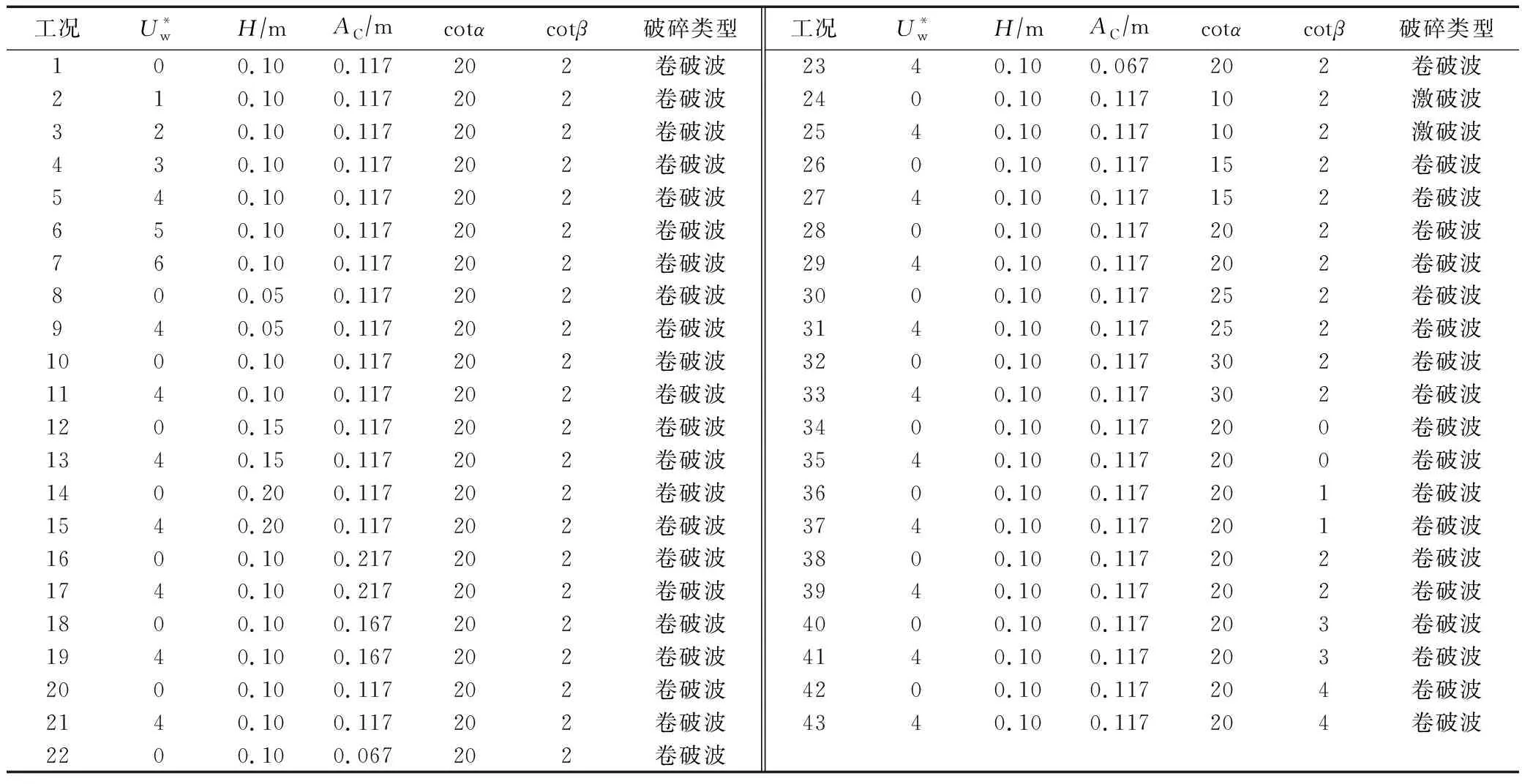
表1 数值模拟工况和波浪破碎类型Tab.1 Parameter setup of numerical simulation and wave breaking types
3.1 水动力特性分析
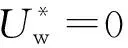

图8 有风和无风时不同时刻水体的速度云图Fig.8 Velocity contours of water body at different time moments in windy and windless conditions

图9 有风和无风时孤立波爬高(a)和越浪量(b)时程曲线对比Fig.9 Comparison of the time series of solitary wave runup height (a) and volume of overtopping water (b) in windy and windless conditions

图10 有风和无风时海堤所受的水动力荷载Fig.10 Hydrodynamic forces exerted at the seawall in windy and windless conditions
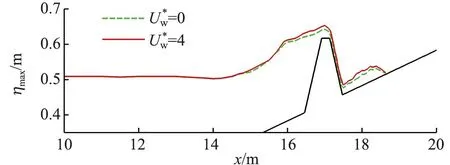
图11 有风和无风时沿程最大水位高程空间分布Fig.11 Spatial distributions of the maximum water elevation in windy and windless conditions
3.2 风速的影响
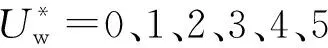

图13 不同风速下孤立波的最大爬高(a)和最大越浪量(b)Fig.13 Maximum runup height (a) and maximum overtopping volume (b) of solitary wave under different onshore wind speeds

图14 不同风速下不同测点处相对波高的比较Fig.14 Comparison of relative wave height for different wave gauges under different onshore wind speeds

图15 不同风速下沿程最大水位高程空间分布Fig.15 Spatial distributions of the maximum water elevation under different onshore wind speeds
3.3 入射波高的影响
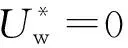
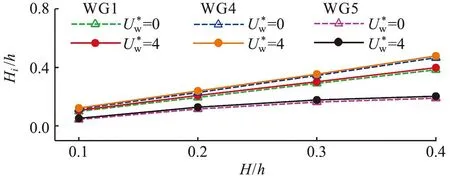
图17 不同入射波高下有风和无风时不同测点处相对波高的比较Fig.17 Comparison of relative wave height for different wave gauges in windy and windless conditions under different incident wave heights
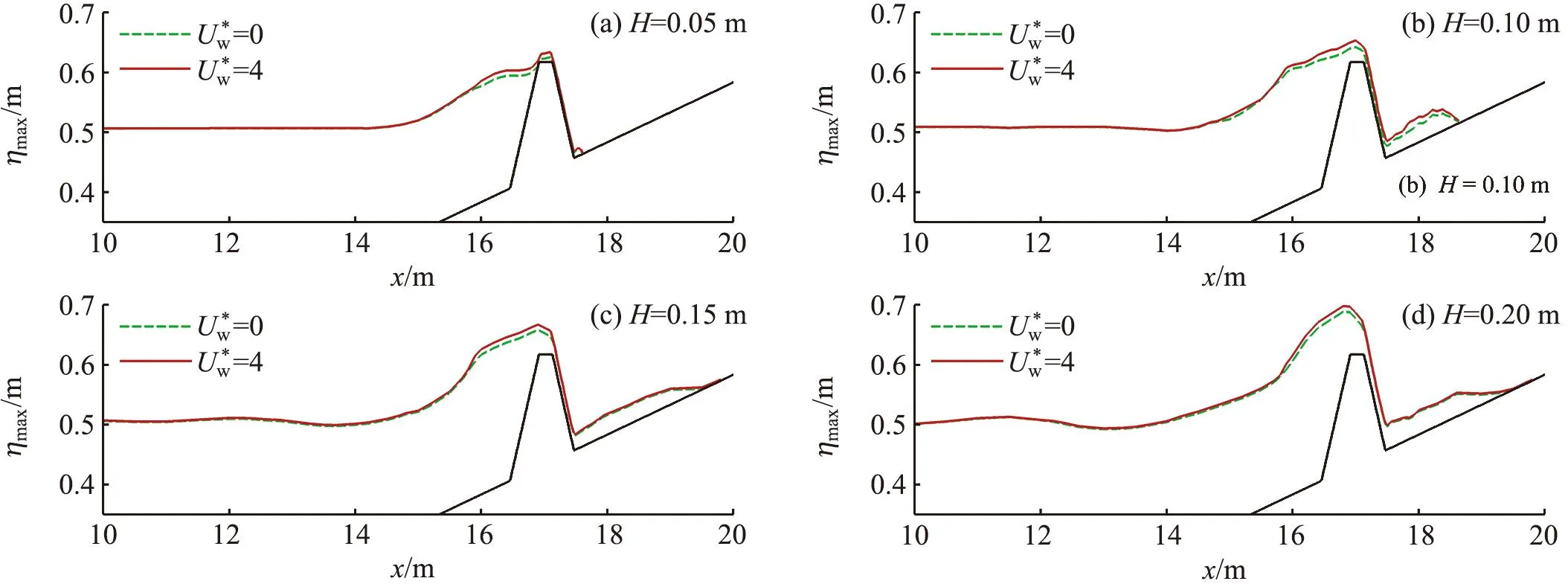
图18 不同入射波高下有风和无风时沿程最大水位高程空间分布Fig.18 Spatial distributions of the maximum water elevation in windy and windless conditions under different incident wave heights
3.4 堤顶超高的影响
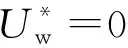

图19 不同堤顶超高下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)Fig.19 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different dimensionless crest freeboards
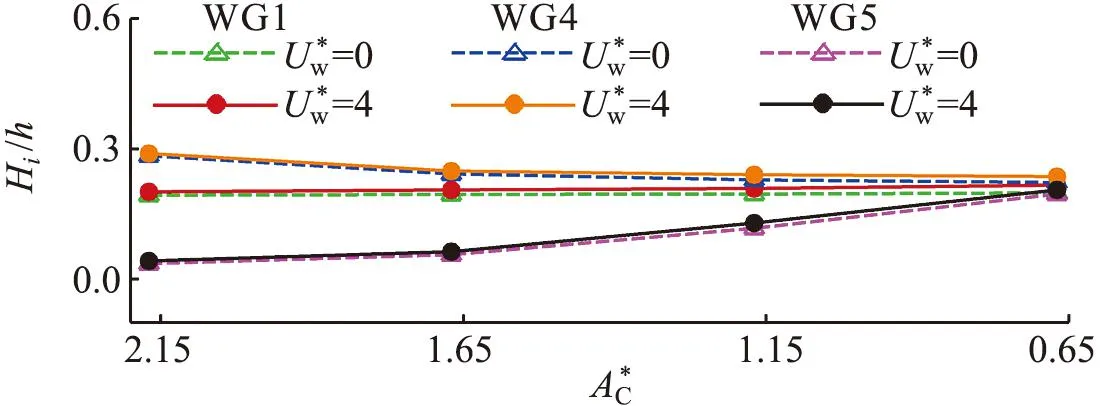
图20 不同堤顶超高下有风和无风时不同测点处相对波高的比较Fig.20 Comparison of relative wave height for different wave gauges in windy and windless conditions under different dimensionless crest freeboards
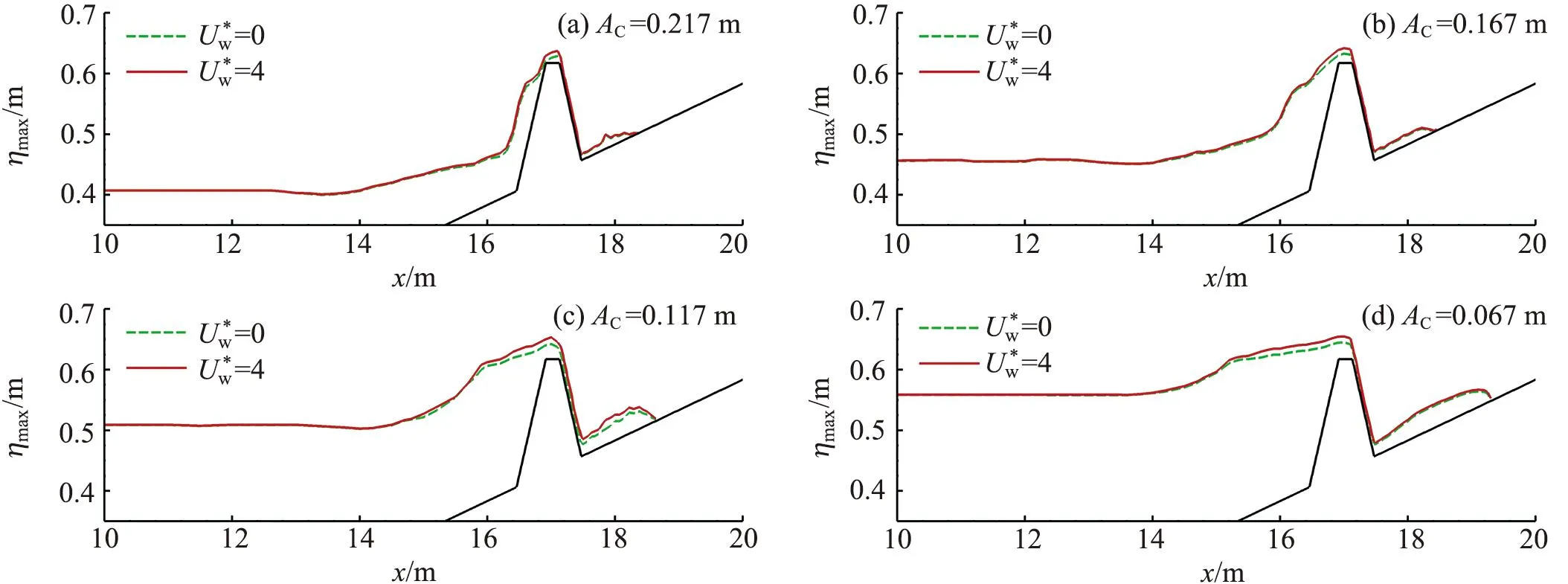
图21 不同堤顶超高下有风和无风时沿程最大水位高程空间分布Fig.21 Spatial distributions of the maximum water elevation in windy and windless conditions under different dimensionless crest freeboards
3.5 岸滩坡度的影响
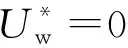

图22 不同岸滩坡度下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)Fig.22 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windlessconditions under different beach slopes

图23 不同岸滩坡度下有风和无风时不同测点处相对波高的比较Fig.23 Comparison of relative wave height for different wave gauges in windy and windless conditions under different beach slopes
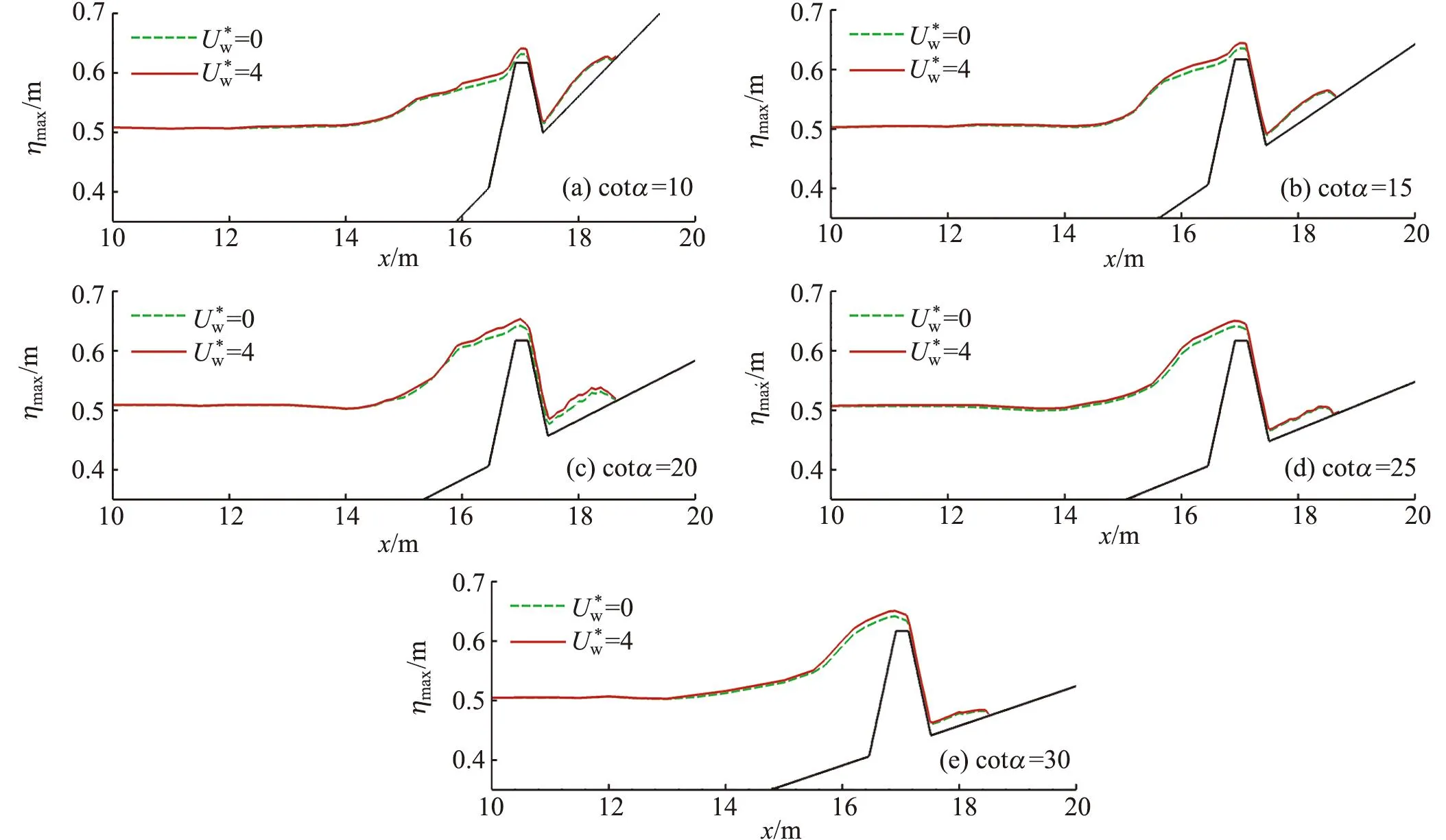
图24 不同岸滩坡度下有风和无风时沿程最大水位高程空间分布Fig.24 Spatial distributions of the maximum water elevation in windy and windless conditions under different beach slopes
3.6 海堤坡度的影响
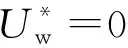

图25 不同海堤坡度下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)Fig.25 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different seawall slopes
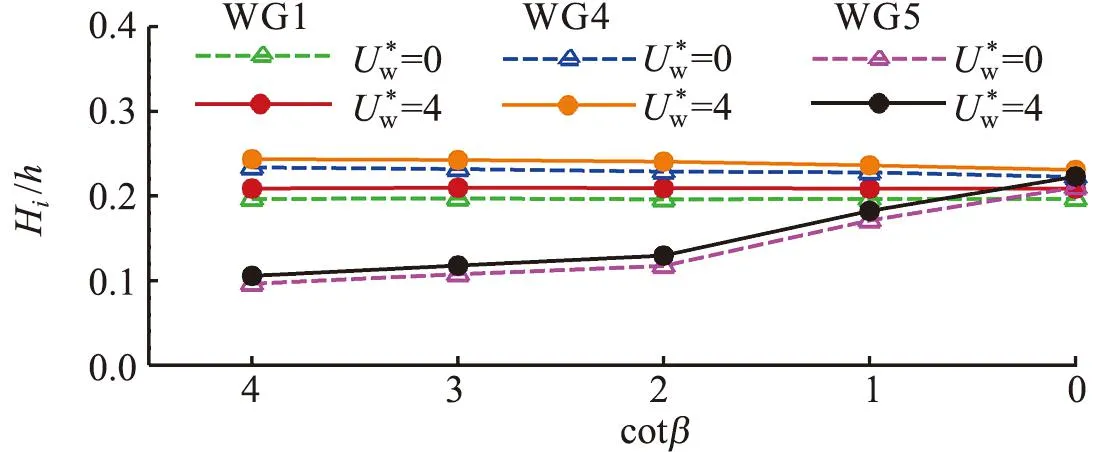
图26 不同海堤坡度下有风和无风时不同测点处相对波高的比较Fig.26 Comparison of relative wave height for different wave gauges in windy and windless conditions under different seawall slopes

图27 不同海堤坡度下有风和无风时沿程最大水位高程空间分布Fig.27 Spatial distributions of the maximum water elevation in windy and windless conditions under different seawall slopes
4 结论
1)有向岸风时,孤立波越浪的水动力特性更为显著,孤立波水体高速流动区域明显增大,破碎时刻和破碎位置均会提前,在海堤上更早地发生越浪过程。
2)随着向岸风风速的增大,孤立波波峰水体流速会增大,孤立波在斜坡式海堤上的最大爬高、最大越浪量以及沿程最大水位高程均有所增大。
3)随着入射波高的增大和堤顶超高的减小,孤立波的最大爬高、最大越浪量以及沿程最大水位高程逐渐增大。
4)随着岸滩坡度的增大,孤立波在岸滩上损失的能量减少,最大爬高、最大越浪量均有所增大。
5)随着海堤坡度的增大(除cotβ=0外),孤立波的最大爬高和最大越浪量分别增大和减小。

