基于人口与经济组合模型的区域能源消费预测
李茂林 李宁宁 宋雯馨





摘 要:为了更好地了解我国东南沿海某地区能源消费的发展趋势,对某区域2010—2020年的人口变化与经济水平变化进行分析,建立连续人口合理变化模型,考虑年龄结构、生育模式、人口出生与死亡率对人口数量增长与人口结构的影响,预测区域人口于2029年达到峰值9195.04万人,基于GM(1,1)对该区域经济水平进行预测,模型后验差比值为0.01,平均相对误差为1.868%,结合2035年与2050年两个时间节点,建立能源消费与人口和经济水平的岭回归模型,模型MAPE为2%,R2为0.93,模型预测效果较好。
关键词:能源消费;人口预测模型;灰色预测模型GM(1,1);岭回归
中图分类号:F713.54文献标识码:A文章编号:1005-6432(2024)03-0012-04
DOI:10.13939/j.cnki.zgsc.2024.03.003
1 引言
在能源经济研究中,能源消费与经济水平之间存在显著影响关系[1],单一预测模型包含信息量有限,容易导致预测结果与实际情况存在偏差,预测精度差[2]。文章关于中国东南沿海某区域建立了经济、人口与能源消费量的预测模型。该区域地势平坦,水陆交通便利,人口较为密集且经济发达、科教资源丰富。以2020年为基期,结合中国式现代化的两个时间节点(2035和2050),预测该区域“十四五”至“二十一五”期间人口、经济(GDP)和能源消费量的变化。为制定合理能源政策、采取合理规划措施提供依据,对合理安排资源配置、推动能源领域的创新发展提供指导。
2 人口预测模型
建立人口变化模型,假设该区域无重大自然灾害发生;短时间内,医疗卫生水平不发生巨大变化、所研究范围内没有太大的人口变动,将出生人口数、死亡人口数、老龄化作为衡量人口状态变化的全部因素[3]。本研究选取2010年至2020年人口数据。
首先对人口的增长与人口结构的发展进行合理的预测,考虑年龄结构、生育模式、人口出生与死亡率对人口数量增长和人口结构的影响。为了简化研究,笔者剔除了移民等其他社会性因素,仅仅专注于自然出生和死亡这两个方面的影响。笔者假定这个地区的人口结构呈正态分布。年龄r与时刻t的关系称为人口分布函数,记作F(r,t),其中t,r(≥0)均为连续变量,设F(r,t)是连续的、可微的。在给定的时刻t,将人口总数记作N(t),最高年龄记作rm,rm→SymboleB@
时,有:
F(0,t)=0,F(rm,t)=N(t)(1)
不同年龄r在时刻t下的死亡率函数关系记作μ(r,t),记p(r,t)dr为年龄在[r,r+dr)内单位时间t的死亡人数。为了找出p(r,t)满足的公式,笔者需要考察那些年龄处于[r,r+dr)区间并在t到t+dt时间段内仍然存活的个体,他们的年龄变为[r+dr1,r+dr+dr),这里dr1=dt。与此同时,考虑到dt时间内死去的一部分人群数量可通过μ(r,t)p(r,t)dr dt找到,于是:
[p(r+dr1,t+dt)-p(r,t+dt)]dr+[p(r,t+dt)-p(r,t)]dr=-μ(r,t)p(r,t)dr dt (2)
且dr1=dt,可得到关于人口密度函数p(r,t)的一阶偏微分方程,其中死亡率为已知函数。即:
pr+pt=-μ(r,t)p(r,t)(3)
式(3)中,初始人口密度p(r,0)=p0(r),单位时间出生的婴儿数量,即人口出生率记作p(0,t)=f(t),该区域的p0(r)可由统计调查资料得到,是已知量;人口出生率f(t)对预测和控制人口结构与数量的变化起着重要作用,对该区域的人口出生数量进一步分析。将式(3)及定解条件写作:
pr+pt=-μ(r,t)p(r,t)p(r,0)=p0(r)p(0,t)=f(t)(4)
式(4)说明了人口连续发展历程,确定密度函数p(r,t)后,可以推断出现有的人口分布状况函数如下:
F(r,t)=∫r0p(s,t)ds (5)
为使式(4)的求解更加符合实际情况,这里给出在社会安定的局面下,死亡率与时间無关,假设μ(r,t)==μ(r)。这时式(4)的解为:
p(r,t)=p0(r-t)e-∫rr-tμ(s)ds,0≤t≤rf(t-r)e-∫ro μ(s)ds,t>r(6)
在式(4)和式(6)中,笔者通过调查数据获取到对应的p0(r)和μ(r)数值。与此同时,μ(r,t)可以通过对μ(r,0)进行粗略的估计得到。在人口预测和控制的过程中,关键要关注出生率f(t)的变动,需要深入了解人口中的性别比率,也就是k(r,t),指的是某一时间点t下,在某特定年龄段[r,r+dr)的女性人口数量比率。假设适孕年龄区间为[r1,r2],那么笔者定义k(r,t)p(r,t)dr代表的是一个单位时间内处于该年龄段的女性的生育率,所以:
f(t)=∫r2r1b(r,t)k(r,t)p(r,t)dr(7)
将b(r,t)定义为
b(r,t)=β(t)h(r,t)(8)
其中h(r,t)满足
∫r2r1h(r,t)dr=1(9)
于是
β(t)=∫r2r1b(r,t)dr(10)
f(t)=β(t)∫r2r1h(r,t)k(r,t)p(r,t)dr(11)
通过式(10)可以看出,β(t)描述的是每一个育龄女性在某一段时间内的平均生育次数,也称为生育率。从式(8)与式(9)中可得知,h(r,t)表示具有特定生育水平的所有妇女。当环境相对稳定的时候h(r,t)=h(r)。常采用的h(r)形式是借用概率论中的Γ分布[4]。
h(r)=(r-r1)α-1e-r-r1θθαΓ(α),r>r1(12)
并取θ=2,α=n/2,这时有:
rc=r1+n+2(13)
晚婚、晚育是影响人口的重要因素,文章关于晚婚晚育研究基于式(11),用于描绘单位时间内出生的孩子的数量。这一框架包括了死亡率函数μ(r,t)、性别比率k(r,t)以及最初人口密度函数p0(r),这些数据可以通过查阅相关统计数据得出。此外,可通过调控生育率β(t)和生育趋势h(r,t)来调整该区域整个群體的人口演变过程。前者β(t)影响着总体出生人数,h(r,t)则会影响家庭选择何时生育以及何时停止生育的选择性倾向[5]。模型预测结果如图1所示。
图1 不同年份下人口数量预测
3 经济预测模型
国内生产总值是反映经济总体状况的指标。文章选用灰色关联度分析对某区域GDP进行预测。运用具体的灰色系统行为特征数据,挖掘和利用其中的所有相关信息(包括明示的信息和潜在的信息),探寻各种因素之间的数学关联以及这些因素自身之间的数学规律,GM(1,1)是一种被广泛使用的灰色系统分析与预测方法[6],相比于其他传统的预测模型,GM(1,1)需要的数据量较少,选用某区域2010至2020年的数据,灰色预测模型得到级比检验结果,如表1所示。
原序列的所有级比值都位于区间(0.846,1.181)内,说明适合构建灰色预测模型。灰色预测模型预测结果如图2所示。
图2 灰色预测模型预测结果
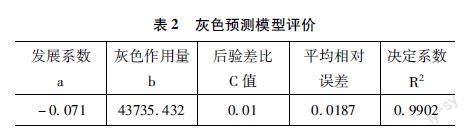
文章构建的模型后验差比值为0.01,预测精度较高,平均相对误差为1.868%,决定系数R2为0.9902,拟合效果评价如表2所示。
4 基于岭回归模型的能源消费量预测模型
建立能源消费量与某区域人口与经济的关系,将能源消费量作为自变量,人口与经济因素作为因变量,利用SPSS软件对2010—2020年的数据做线性回归模型,结果如表3所示,可以得到人口数量与GDP的VIF为12.392,存在共线性,故选用岭回归。
岭回归是一种在自变量高度相关的情况下估计多元回归模型系数的方法。它在普通最小二乘法的基础上,通过对模型的系数增加约束来减小参数的方差,从而降低预测误差。当线性回归模型具有一些高度相关的独立变量时,岭回归为最小二乘法估计不精确的一种可靠的解决方案[7]。
构建岭回归参数步骤:①输入参数x、y和lam,分别表示自变量的矩阵、因变量的矩阵和岭参数。②计算自变量矩阵x的转置与自身的乘积,得到xTx。③获取矩阵xTx的行数和列数,分别赋值给变量m和n。④构建一个临时矩阵temp,它是xTx加上一个单位矩阵乘以岭参数lam。这个步骤是为了在计算逆矩阵时避免出现奇异矩阵。⑤通过判断临时矩阵temp的行列式是否为零,来判断矩阵是否可逆。如果行列式为零,说明矩阵奇异,无法进行逆矩阵的计算。⑥如果矩阵可逆,通过计算temp的逆矩阵与x的转置矩阵的乘积,再与因变量矩阵y相乘,得到标准系数w。⑦将计算得到的标准系数w返回作为函数的输出。
通过添加岭参数来解决自变量矩阵不可逆的问题,并计算出标准系数w[8]。在对能源消费量进行岭回归时,对2010—2020年的数据进行标准化处理,求出不同岭参数下的标准系数存放在weights矩阵中,画出随着参数lam变化的岭迹图,结果如图3所示。
将标准化系数反标准化,求出实际系数,在最小误差下,得到的多元线性岭回归方程为:
y=-31168.42+6.784·人口+0.062·GDP
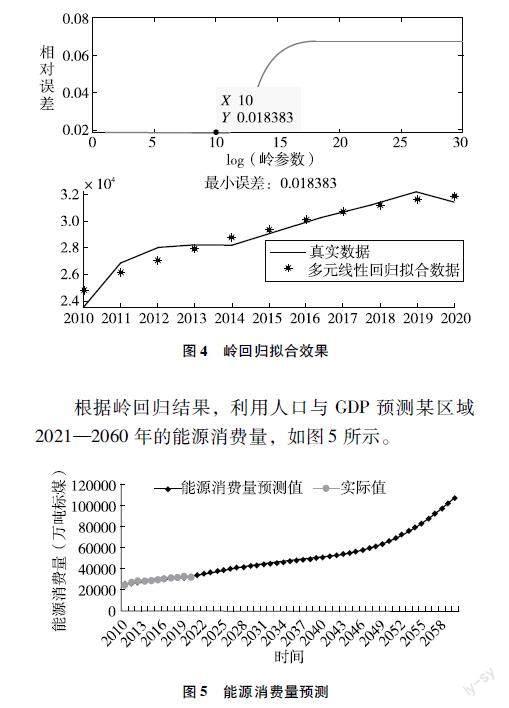
文章构建的方程平均绝对百分比误差MAPE为2%,决定系数R2为0.93,拟合效果如图4所示。
根据岭回归结果,利用人口与GDP预测某区域2021—2060年的能源消费量,如图5所示。
5 结论
第一,文章建立的连续人口预测模型是基于基本假定条件下,预测结果表明该区域人口预计在2029年达到峰值9195.04万人,后呈现下降趋势,符合我国人口基本变化情况。
第二,基于灰色预测模型GM(1,1)平均相对误差为1.868%,决定系数为0.9902,准确性较高。由于样本数量较少,该模型的稳定性仍有提升的空间。
第三,文章通过组合模型预测能源消费量,预测人口与经济水平,构建基于岭回归的能源消费量预测模型,MAPE为2%,决定系数R2为0.93,模型预测效果良好。
参考文献:
[1]KAMALJIT S,SIMMI V. Relationship trend of energy consumption and economic growth studies: a global examination based on bibliometric and visualization analysis[J].International journal of energy sector management,2023,17(2).
[2]WU G,ZHANG L,LIN T, et al. Forecast of total rural energy demand based on energy consumption intensity[R].Frontiers in energy research,2023.
[3]李志强,董娟,李骏鹏.基于生育转变理论的人口年龄结构预测[J].价格理论与实践,2022(6):68-72.
[4]田永强,黄洪旭.云南省出生人口预测及其经济影响因素研究[J].现代商贸工业,2022,43(18):84-86.
[5]宋晓敏,周海燕,王静,等.微分方程在成都市人口预测中的应用[J].内江科技,2022,43(1):59-61.
[6]任俊娟.基于GM(1,1)模型的CPI经济预测[J].统计与决策,2012(13):75-76.
[7]师佳,宁俊.我国纺织服装行业碳排放影响因素及达峰预测[J].北京服装学院学报(自然科学版),2022,42(3):66-74.
[8]薛慧芳.转型发展视角下山西省能源消费预测[J].山西能源学院学报,2019,32(6):54-56.

