复杂荷载作用下海上风机故障停机分析
陈 松,李志川,邳 帅,朱永飞,曹柏寒,卢东哲,王文华,李 昕
(1.中海油能源发展股份有限公司清洁能源分公司,天津300459;2.大连理工大学,辽宁大连116024)
0 引 言
海上风电是风电产业未来发展的重要方向,也是我国能源结构转型的重要支撑。然而,我国海上风能资源开发不仅面临严酷的海洋环境,部分地区还面临地震的威胁,比如我国环渤海海域、江苏沿海及台湾海峡等均为地震高烈度区。从当前已建的海上风电项目以及未来规划来看,多数海上风电场址位于这些地震带附近,潜存着较高的地震破坏风险。因此,国内外学者围绕风、浪、地震作用下海上风机结构动力响应特性开展了一系列研究,闫阳天等[1]采用多体动力学-有限元结合方法研究了地震及湍流风联合作用下DTU 10 MW近海桩柱式风力机塔架动力学响应特性,表明风荷载的变化会显著影响地震作用下风机结构动态响应。Yang等[2]和李颖等[3]进一步开展地震、风和波浪联合作用下的海上风力机整体耦合分析,系统地研究气动阻尼、环境荷载以及控制策略对受到地震作用下海上风机的结构响应的影响。Zheng等[4]通过开展规则波或不规则波和地震作用下海上风机整体结构动力模型试验,指出地震和波浪的联合作用对正确评估结构反应具有重要的意义。此外,Moan等[5]进行了在不同地震、风和波浪荷载组合条件下五桩海上风机模型的动力试验和数值分析,验证得出海上风机地震响应必须分析风荷载、波流荷载与海上风机结构之间的相互作用。
海上风场环境恶劣,大型风电场的控制形式复杂,外部和内部条件都有可能造成风机在发电过程中发生故障。其中,一些故障情况会在短时间内显著增加支撑结构受到的载荷,严重的甚至会造成结构的失稳和破坏[6]。Jiang等[7]、安利强等[8]和李嘉文等[9]利用耦合分析方法研究了海上风机变桨故障后紧急停机的动力响应,发现顺桨速率对风机系统的运动和内力有显著的影响,并且变桨故障下紧急停机会使风机系统的动力响应增大。
国内外学者虽然分别在地震作用和故障状态下开展了海上风机结构动力响应分析,但是针对风、浪、地震作用下海上风机发生故障并主动停机的动力研究很少。并且,海上风机技术规范DNV GL-ST-0437[10]也明确规定了海上风机地震反应分析应考虑正常运行和发电机断网等不同风机运行以及典型故障状态。可见,研究风、浪、地震作用下故障停机过程对海上风机的动力响应以及结构安全性的影响十分重要。因此,本文基于FAST v8[11]开发地震分析模块[5]建立了气动-水动-地震-伺服-结构的全耦合分析模型,模拟了发电机断网并由此引发风机主动顺桨停机的过程,开展风-浪-地震-故障海上风机整体耦合分析,利用小波时频分析方法探究该过程海上风机结构动力响应机理。
1 基本理论
1.1 气动-水动-地震-伺服-结构的全耦合时域分析
利用FAST v8软件建立的气动-水动-地震-伺服-结构全耦合分析模型如图1所示,选取叶片展向前两阶模态、弦向一阶模态和塔筒顺风向、侧风向前两阶弯曲模态作为主自由度,基于多体动力学理论建立了转子机舱组件和塔筒结构的数值仿真模型,与此同时,采用线性梁单元模拟固定式海上风机基础结构。此外,通过在塔筒和基础结构之间的指定了一个过渡节点以考虑转子机舱组件和支撑结构之间的相互作用。转子叶片和基础结构杆件所受的气动和水动力荷载,分别采用叶素动量理论[12]和莫里森方程[13]计算。同时,根据输入的地震波加速度时程采用式(5)计算出作用在风力机结构的地震力[5]。
叶素动量理论为
(1)
(2)
Vx=Vw(1-α)
(3)
式中,{Fr|AeroB}为叶片的气动荷载向量;ρair为空气密度;Nb为转子包含的叶片数量;Vrel、Vx和Vw分别为相对风速、轴向风速和来流风速;CL和CD为叶片升力和阻力系数;c为叶片弦长;Ω为转子转速;φ为入流角;r为叶素中心与轮毂中线间距;dr为叶素长度;a′和a分别为切向和轴向诱导系数。
莫里森方程为
(4)

(5)

1.2 时频分析方法
小波变换作为一种新型的时频分析工具,与传统的短时傅里叶变换不同,它在时域和频域均具有表征信号局部特征的能力[14]。小波分析的基本思想就是选取一族函数去表示或者逼近某一信号,这一族小波函数称为小波函数系,它是通过基本小波函数的不同尺度的平移和伸缩构成的。设ψ∈L2(R),L2(R)是为平方可积的实数空间,即能量有限的空间信号。则函数族可表示为
(6)
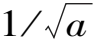
ψa,τ(t)为依赖于参数a、τ的小波基函数,它们是由同一母函数ψ(t)经过伸缩和平移后得到的一组函数序列。对f∈L2(R)信号f的连续小波变换Ff(a,τ)的定义为
(7)
式中,Ff(a,τ)为f(t)和ψa,τ(t)的卷积;a和τ均为连续的变量。
进一步,如果对于离散时间序列xn来说,xn∈L2(R),信号x(t)的小波变换Fn(a)只由一个尺度参数a决定,Fn(a)定义为xn与母小波函数ψ0(μ)在缩放、平移后的卷积形式,即
(8)
式中,nt+1、nt为时间序列;N为时间序列点的个数;μ为无量纲时间参数;a为小波尺度参数;ψ为母小波ψ0无量纲化的结果;*表示复共轭;Δt为时间步长。
在小波变换的实际应用中,母小波函数的选取对分析结果至关重要。对于处于复杂环境载荷中的海上风机结构而言,应首选Morlet小波[15],这是一个由高斯包络的复平面波,在时域和频域中都具有很好的局部性,其表达式为
(9)
式中,ω0为小波中心的圆频率。
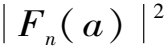
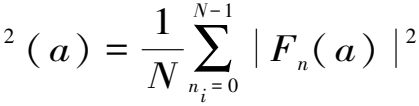
(10)
式中,ϖ2(a)为全局小波能量谱,可以给出占优势的周期分量的强度信息。
在本文中,离散小波变换Fn(a)定义为环境载荷作用下海上风机结构响应时间序列与Morlet母小波函数在缩放、平移后的卷积。
2 10 MW海上风机模型
2.1 模型设计参数
以丹麦科技大学设计的DTU 10MW基准风机[16]为研究对象,根据我国东南沿海地区实测的海洋环境条件,对DTU 10MW风机的塔筒重新设计,将塔筒高度调整为85.48 m。风机系统和塔筒的附加基本参数如表1所示。此外,为了保证风机系统在40 m水深下的稳定运行和结构安全设计了导管架式基础结构。沿4个导管架桩腿布置了4层X形斜撑和泥面撑杆。导管架基础顶部和底部的宽度分别为12 m和15 m,导管架基础结构高度为70.15 m。基于FAST v8所建立的样本风机模型采用等效桩来模拟桩土相互作用的影响,等效桩长度为7.5倍桩外径。关于支撑系统的详细参数如图2所示,其中,D为外直径;T为壁厚。

表1 10 MW风电机组基本参数
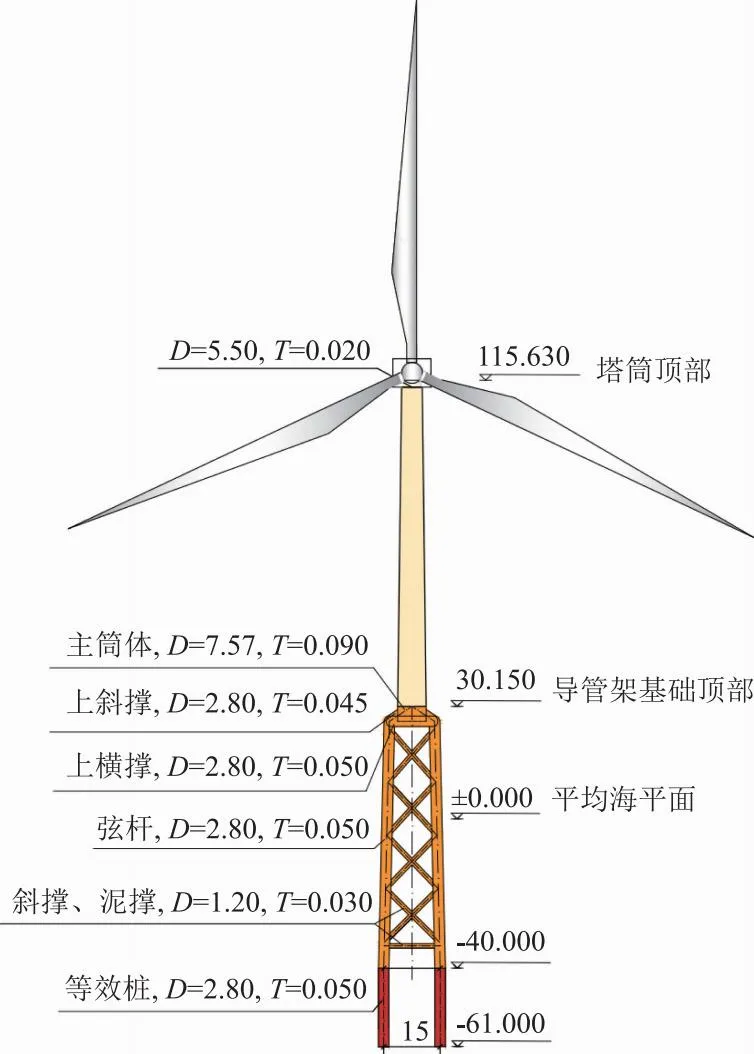
图2 海上风机设计参数(单位:m)
2.2 设计工况
依据海上风机技术规范DNV GL-ST-0437[10]建议的组合工况DLC 11.1和11.2可知,对于海上风机结构设计不仅要考虑正常运行状态下地震、风、浪荷载组合,还应同时考虑发电机断网等典型故障状态。参考中国东南部某海域地区抗震设防烈度为7度,设计基本地震加速度为0.10g。此外,考虑到地震随机性以及固定式海上风机结构的低阶特征频率基本在0.1~10 Hz范围内,选取El Centro(El C)、Taft、Borrego和Kocaeli等4种实测地震波[17],对应的地震波加速度时程和傅里叶谱分别如图3所示。
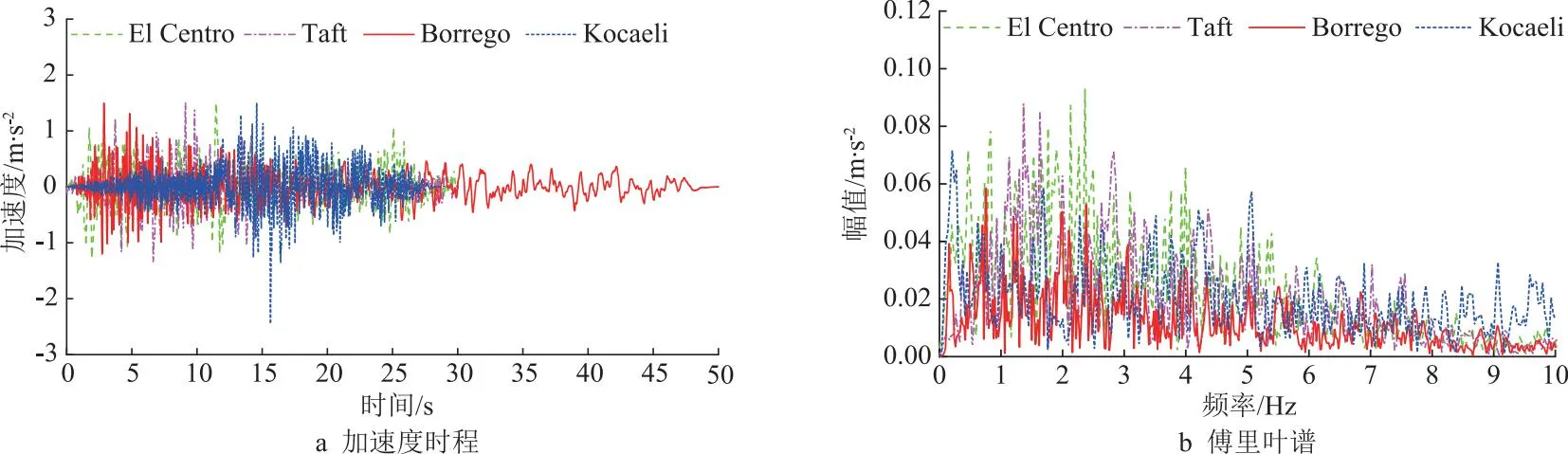
图3 实测地震波
为了能够清晰地揭示风、浪、地震作用下海上风机故障并主动停机过程中结构响应机理,本文选用稳态风和规则波与所选取实测地震波进行荷载组合。LC1~LC 4和LC5~LC 8工况中整体耦合计算前100 s(t<100 s),风机结构在风浪作用下处于正常运行发电状态;当数值仿真时间达到100 s时(t≥100 s),分别在图1所示的泥面处施加相应的实测地震波加速度时程。二者的区别在于在100 s施加地震作用后,LC1~LC4中风机结构仍然处于正常运行状态,而LC5~LC8风机结构发电机断网,同时启动主动顺桨停机策略,即高速传动轴制动且风机叶片以9°/s的顺桨速率快速顺桨至90°,本文选取的计算工况如表2所示,其中,地震波的峰值加速度均为0.15g,风、波浪和地震的作用方向均为图1所示的顺风向(X方向)。
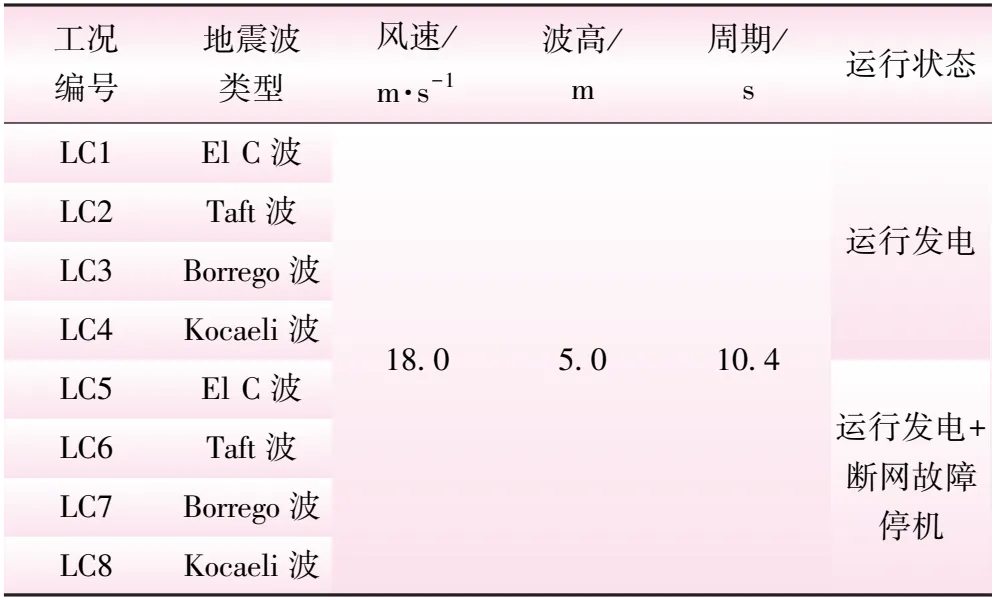
表2 设计工况
3 风、浪和地震作用下海上风机故障停机时耦合响应分析
3.1 特征模态分析
在进行风、浪和地震联合作用下海上风机故障停机动力响应分析前,首先采用谱分析方法确定海上风机整体耦合模型的固有频率和特征模态。对于所建立的整体耦合模型,海上风机转子叶片及支撑结构(塔筒及基础结构)材料阻尼比分别为0.5%和1.5%,故可视为小阻尼结构体系。因此,可采用高斯白噪声激发海上风机结构特征模态。通过所开发地震模块将高斯白噪声沿顺风向作用于海上风机整体耦合模型。沿图1所示的海上风机支撑系统高度选取节点,基于所选节点的运动响应频域响应谱得到顺风向前2阶频率分别为0.29 Hz和0.80 Hz,相应的归一化振型如图4所示。根据各阶振型沿支撑系统高度变化规律可知,顺风向第1阶振型幅值位于塔筒顶部,第2阶振型幅值则位于塔筒底部位置。
3.2 动力响应分析
应用风-浪-地震-故障全耦合分析模型,对风、浪、地震作用下导管架式海上风机发电机断网故障停机情况展开研究。为了更好的对比分析复杂荷载作用下海上风机故障停机时的动力响应,本文还开展了风机系统在风、浪、地震作用下一直处于正常运行状态(未发生故障)的耦合仿真计算。所考虑的海洋环境条件为:轮毂处稳态风风速为18 m/s;规则波波高为5.0 m,波周期为10.4 s。
特选取包含地震作用前、地震作用过程中以及地震作用结束后3个阶段的90~190 s的结构响应时程进行整个动力响应分析,对应3个阶段的塔顶位移和倾覆力矩的时域统计值分别如图5、6所示。同时,为了定量评价风、浪、地震作用时正常运行和故障停机2种情况下结构响应的变化程度,定义结构响应统计值变化率为
(11)
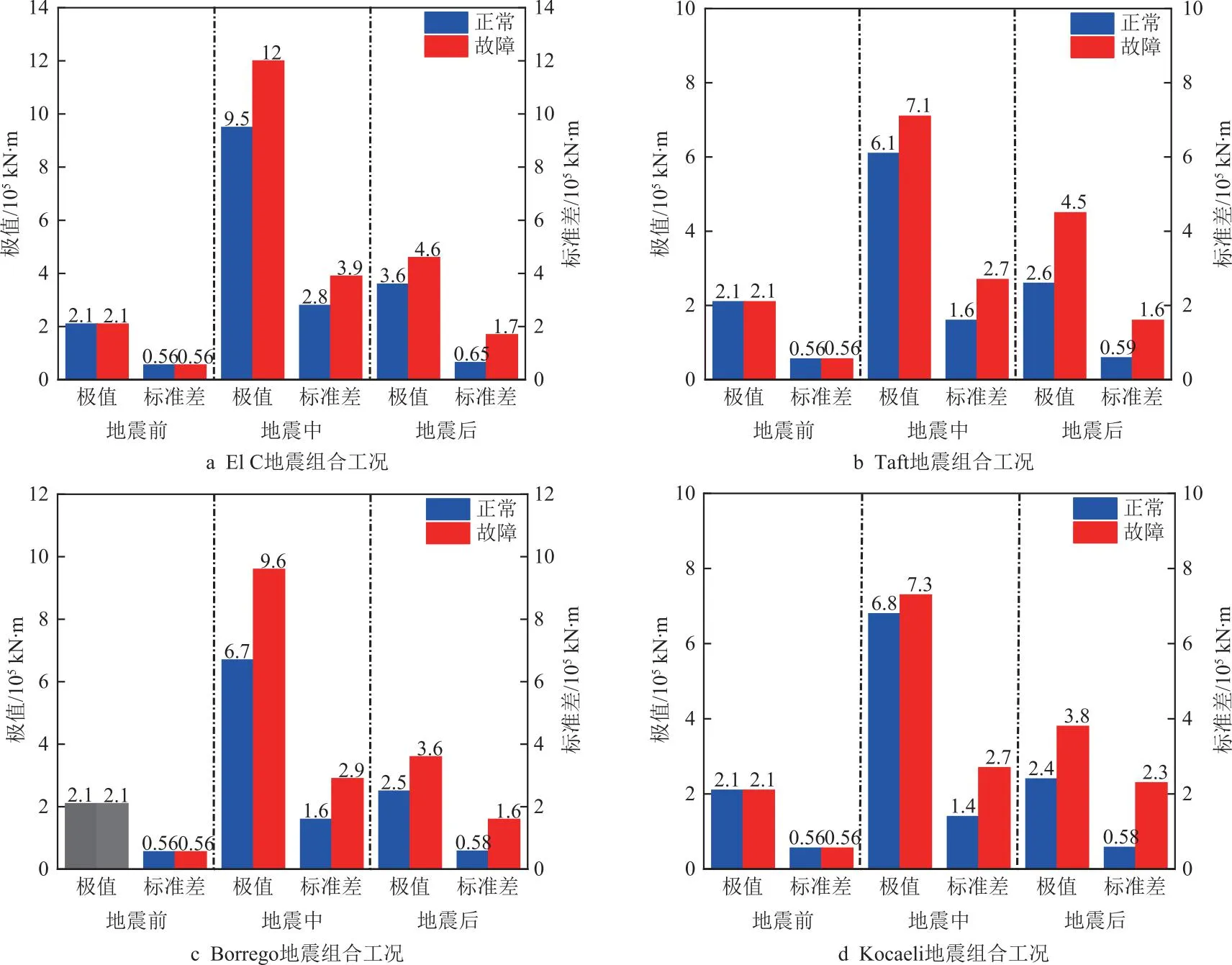
图6 不同组合工况下倾覆力矩统计值
式中,Δ为结构响应变化率;β故障、β正常分别为故障停机和正常运行时结构响应统计值。
由于整个模拟过程包含了地震作用前、中、后3个过程,因此海上风机结构响应具有时变性。同时,发电机断网故障并启动顺桨停机策略时,海上风机运行状态随时间发生显著变化。传统的傅里叶变换无法有效地反映出结构响应频域特性随时间的变化,因此有必要采用小波变换理论对海上风机结构响应进行时频分析,从而更加精细地得到风、浪、地震作用下海上风机发生故障并主动停机时的动力响应机理。利用小波能量谱对海上风机结构响应进行分析时,时频图中颜色的深浅代表某一频率某一时间的能量的大小,蓝色代表能量小,能量越大颜色越亮。以Kocaeli地震组合工况为例,正常运行和故障停机2种情况下塔顶位移和倾覆力矩的时程对比和时频分别如图7、8所示。

图7 Kocaeli地震波组合工况下塔顶位移时程及时频
3.2.1 塔筒顶部位移
图5中列出了4种地震组合工况下海上风机处于正常运行和故障停机2种情况下塔顶位移在地震作用前、中、后3个阶段的统计值。由图5可知,地震作用阶段2种情况下塔顶位移响应统计值最大,说明地震激励可显著增大海上风机结构运动响应。进一步,故障停机情况下的塔顶位移响应统计值大于正常情况下的塔顶位移响应统计值。可见,地震作用下发电机断网故障时,启动顺桨停机控制策略会增大塔顶位移响应。其中,Borrego地震波作用过程中故障停机使塔顶位移极值放大最显著,如图5c所示,根据式(11)计算得到故障停机使塔顶位移极值增大约为77%。因此,地震作用下顺桨停机控制策略对海上风机运动响应的放大应该引起重视。此外,在地震作用结束后,正常运行状态下的塔顶位移响应迅速减小到与地震作用之前的较为一致,而故障停机情况下海上风机结构仍具有较大的塔顶位移响应。根据上述内容可知,风、浪、地震作用下故障停机情况中海上风机结构响应变化较为复杂,因此,需要对结构响应进行频域内的深入分析。
以Kocaeli地震组合工况为例,利用式(8)~(10)对90~190s的塔顶位移时间序列进行小波变换,进而得到对应于图7a所示的整个塔顶位移响应时程序列的全局小波能量谱。图7b、7c分别给出了正常运行和故障停机2种情况下塔顶位移响应能量峰值出现的时间和频率位置。对于正常运行状态下,地震作用过程中塔顶位移响应主要受到海上风机结构的二阶(0.80 Hz)频率分量的影响,特别是在地震波幅值最大时,小波能量谱的颜色最亮,塔顶位移响应的二阶频率的能量最大。而当发电机断网故障时,则观察到不同的频域特性,自启动停机顺桨策略时便激发了海上风机结构基频(0.29 Hz),该频率分量对塔顶位移响应的影响十分显著,并且这种影响一直延续至190 s,正是由于停机顺桨所激发的海上风机结构基频的存在导致故障停机时的塔顶位移响应大于正常运行的情况。此外,在图7c中可以观察到海上风机基频能量谱的颜色亮度随时间逐渐减小,基频对塔顶位移响应的影响逐渐弱化,这主要是受到海上风机系统中阻尼的影响。
3.2.2 倾覆力矩
4种地震组合工况下倾覆力矩统计值如图6所示,地震作用前仅有风浪联合作用时,海上风机结构倾覆力矩具有明显的波动性。地震作用阶段,2种情况下海上风机结构倾覆力矩的统计值均显著增加,特别是El C地震组合工况。同时值得注意的是,相比正常运行情况,故障停机的情况下倾覆力矩的极值和标准差均有所增加,特别是对于Borrego地震作用过程中故障停机情况倾覆力矩的极值增大约43%,如图6c所示。地震作用结束后,故障停机情况下的海上风机结构的倾覆力矩的极值和标准差仍显著大于正常运行情况。
采用小波变换理论对90~190s的倾覆力矩时间序列进行时频分析,得到Kocaeli地震组合工况下正常运行和故障停机两种情况的时频图分别如图8b、8c所示。由图8b和8c可知,2种情况下地震波作用前、中、后3个阶段的倾覆力矩均显著受到波频(0.1 Hz)的影响。而在地震作用阶段,2种情况下倾覆力矩还受到海上风机结构的基频(0.29 Hz)和二阶固有频率(0.80 Hz)和的影响。与正常运行情况不同的是,故障停机情况下启动顺桨停机控制策略显著激发出海上风机结构的基频(0.29 Hz),并且基频对倾覆力矩响应的显著影响一直延续到地震作用结束后,这就导致了地震作用后故障停机工况下倾覆力矩的统计值仍大于正常运行的情况。

图8 Kocaeli地震波组合工况下倾覆力矩时程及时频
4 结 论
基于FAST v8建立的气动-水动-地震-伺服-结构全耦合分析模型,模拟了海上风机结构发电机断网并顺桨停机的过程,开展了风-浪-地震-故障海上风机整体耦合分析。之后,利用小波变换得到塔顶位移和倾覆力矩的小波能量谱进行时频分析,揭示了风、浪和地震作用下故障停机过程中海上风机结构动力响应机理。
(1)地震作用时海上风机结构的二阶固有频率对结构响应的影响十分显著,使得处于正常运行状态和故障停机状态下的海上风机结构响应均显著增大。断网故障情况下启动顺桨停机策略后海上风机结构的动力特性发生显著的变化,相比于正常运行情况,故障后停机顺桨使海上风机结构动力响应进一步放大,比如Borrego地震作用过程中故障情况中倾覆力矩的极值增大约43%。因此海上风机结构安全性设计应该充分考虑风、浪、地震联合作用时故障停机的情况。
(2)故障情况下海上风机在地震作用过程中以及地震作用结束后动力响应均显著增大,这主要是由于结构响应除了受到二阶固有频率的影响,受顺桨停机所激发的海上风机结构基频的影响也十分显著,并且基频的影响一直延续到地震作用结束后。进一步还能观察到海上风机系统中阻尼对结构固有频率小波能量谱峰值的削弱作用。
(3)通过上述统计和时频对比分析可知,地震作用下故障停机时,海上风机结构响应显著增大,这可能会造成结构发生破坏,因此应该采取必要的措施去降低这种情况下海上风机结构响应,比如振动控制方法。此外,为了更加准确地模拟海上风机在复杂环境荷载作用下结构响应机理,未来可开展随机风浪-地震-故障工况下海上风机全耦合动力分析。

