基于改进JRD及误差修正的轴承剩余寿命预测方法*

刘玉山,张旭帮,王灵梅*,孟恩隆,郭东杰

(1.山西大学 自动化与软件学院,山西 太原 030006;2.国家电投集团 山西新能源有限公司,山西 太原 030006)

0 引 言

随着风电机组运行年限的增加,那些较早投产的机组即将面临退役。而齿轮箱作为风电机组传动链的关键部件之一,长期处于变工况、非平稳运行状态,故障率较高。

为了指导运维和最大限度地延长机组寿命,需要对齿轮箱关键部件如轴承的异常状态及剩余寿命进行准确预测。

通常情况下,轴承RUL预测包括两部分:

1)退化指标构建。LI Nan-peng等人[1]提出了自适应首次预测时间,并利用粒子滤波降低随机过程的随机误差来改进指数模型。LEI Ya-guo等人[2]建立了考虑多重机械退化因素的随机过程,并利用卡尔曼滤波估计系统状态预测RUL。

近年来,基于神经网络的退化指标被用于轴承RUL预测。RAI A等人[3]提出了利用健康状态下提取的振动特征对自组织神经网络进行概率训练的方法,然后利用检测样本构建了健康指标,采用状态方程模型预测RUL。YU Jian-bo[4]将高斯混合模型与K-means聚类算法相结合,以此来选取故障特征,利用自组织神经网络对数据分布空间进行了建模,把对数似然概率作为健康指标。张全德等人[5]采用自组织神经网络对所提取的原始振动信号特征进行了训练,对比健康状态与待检测状态的最小量化误差,以判断轴承健康状态;但是,上述退化指标容易受噪声干扰出现异常波动,在实际生产中容易造成误报,影响维护人员的决策判断。为此,GUO Wei等人[6]利用模糊C均值聚类算法和JRD构建了新的健康指标,清晰地区分了轴承的状态。RAI A等人[7]利用高斯混合模型,分别计算了健康与缺陷状态下的样本后验概率,利用JRD构建了退化指标,实验验证该指标可有效识别轴承初始故障;但该指标的单调性会影响轴承RUL预测精度,亟待进一步改进。

2)轴承RUL预测。RUL预测又可分为基于模型的预测方法和基于数据驱动的预测方法。前者根据轴承物理失效机理进行了建模,常用的有Pairs-Erdogan和粒子滤波方法。

LIAO Lin-xia等人[8]采用Pairs-Erdogan模型描述了轴承故障部位的裂纹增长,并采用连续贝叶斯更新方法预测了轴承RUL。丁显等人[9]将粒子滤波算法与维纳过程相结合,对风力发电机组轴承剩余寿命进行了准确预测,并用风电场数据进行了验证。然而,在工业应用中,轴承的失效机制通常多种多样,基于模型的预测方法需要一些先验知识或大量经验数据来初始化模型参数。因此,基于模型的方法在轴承RUL预测中应用有限。

随着人工智能技术的发展,基于数据驱动的方法被广泛用于轴承RUL的预测中,其优点在于可以直接从可用的传感器数据中了解到轴承的潜在退化趋势,无需了解轴承的确切故障机制。例如,利用人工神经网络[10-11]来训练预测模型,然后利用训练好的模型估计轴承的RUL;但是,基于人工神经网络的预测方法往往需要大量数据训练模型,在工程实际中想要获得大量故障数据较为困难。因此,一些学者仍然沿用传统算法对轴承RUL开展预测。例如,何茂[12]对高斯混合模型进行了改进以提高无标签数据的聚类性能,同时引入了JRD构建健康指标,选取RVM不同核宽度以确定最优退化曲线,对轴承的长期寿命进行了预测。张龙龙[13]利用支持向量机分类模型对所提取的时域、频域及熵指标进行了轴承健康状态的分类,并建立了退化期与失效期的支持向量机预测模型。WANG Dong等人[14]利用指数模型拟合相关向量,并外推至失效门限,得到了锂电池RUL。

然而,以上方法并未考虑拟合误差对预测结果的影响,导致RUL预测精度不高。

针对上述问题,笔者提出一种改进JRD及误差修正的双指数模型轴承RUL预测方法。

首先,笔者利用GMM与改进JRD,建立轴承退化指标,以提高指标的单调性与平滑性;同时提出新的预测框架,对从初始健康状态退化至检查时刻的CV值进行相空间重构,以此作为相关向量机(RVM)的训练集,获得相关向量;然后,用双指数模型拟合相关向量,并外推至失效门限,以计算剩余寿命,利用ARIMA模型预测双指数模型的拟合误差;最后,利用山西某风电场的齿轮箱故障振动信号与实验台验证,对退化指标识别故障的有效性进行验证,并对轴承的RUL进行预测。

1 基于GMM-JRD的退化指标

1.1 高斯混合模型

由于轴承的性能退化特征一般呈现多模态的特点,当轴承发生性能退化时往往并没有相应的数据标签对其进行表征。因此,笔者采用高斯混合模型对轴承退化阶段进行建模。

高斯混合模型(GMM)是一种基于无监督学习的聚类方法,它是多个高斯个体的线性组合,能够平滑近似任意复杂的数据分布。

给定样本数据X=(x1,x2,…,xN),N为样本个数,假设每个样本数据均可由多个高斯分布生成,但高斯分布的参数未知,则某一样本的概率密度函数可用GMM模型可表示为:

(1)

GMM的概率密度函数参数可用Θ=(w1,…,wk,μ1,…,μk,∑1,…,∑k)表示。

GMM模型的建立需要根据输入的样本数据求取模型参数Θ,其原理是为每个高斯个体寻找一组参数wk,μk,∑k,使得生成该样本的概率最大。具体方式是采用最大似然估计方法对GMM未知参数进行估计。其对数似然函数表示为:

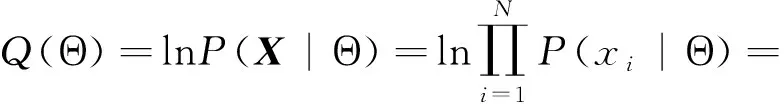
(2)

利用期望最大化算法[15]使式(2)的期望达到最大值。由贝叶斯公式计算样本数据的后验概率公式如下:

(3)

利用下式迭代求解直至Θ收敛得到wk,μk,∑k:

(4)

(5)

(6)

其中式(3)作为GMM模型的输出,为数据样本分配类别后验概率标签,即表示属于该类的概率大小,达到数据聚类的目的。

1.2 杰森-瑞丽散度

香农熵是一种常被用来量化信号信息概率的方法,用以反映系统的各种状态。由于其对数据微小变化不够敏感,因此笔者在此基础上提出瑞丽熵,其定义为:

(7)

式中:Renα(p)为数据样本X=(x1,x2,…,xn)对应的离散概率分布p=(p1,p2,…,pn)的α阶瑞丽熵,当α→1时,上式为香农熵,文献[7]将该指数设为0.5,有较好的分析效果,故笔者设定其为0.5。

杰森-瑞丽散度(JRD)是在KL散度的基础上采用瑞丽熵表示概率分布之间的差异性,JRD距离越小,其概率分布越相似。具体表达式如下:

(8)

式中:p与bi,(i=1,2…,n)为n个概率密度分布及相对应的权重系数,p=(p1,p2,…,pn)。

通常将概率密度函数的权重系数bi设置为均匀型权重,即1/n,而权重bi对指标的平滑性具有重要影响。文献[16]指出采用均匀型权重的JRD易受噪声干扰,导致指标平滑度、单调性较差。

为了降低噪声对JRD的影响,笔者引入指数型权重,并将其应用于轴承性能退化指标的构建中。

指数型权重如下:

(9)

式中:λ为平滑因子,主导着JRD的平滑程度。

由上式可知:当λ=0时,即为均匀型权重。

为了准确描述轴承的退化趋势,笔者对JRD指标进行标准量化处理。通常采用的是归一化方法,将其映射到[0-1]的范围内,得到量化指标置信值CV。

笔者采用如下的归一化方法[12],其公式为:

CV=1-tanh2(JRD)

(10)

性能退化量化指标CV为1时表示轴承处于健康状态,为0时表示失效状态。笔者设定初始故障CV阈值为0.99,失效门限CV阈值为0.4。性能退化指标的实时变化用于反映轴承故障程度的变化,即随着故障程度的加深,性能退化指标也呈现相应下降趋势。

2 双指数预测模型构建

笔者所采用的训练样本RVM回归模型可表示如下:

(11)

式中:X为输入向量,x=(x1,x2,…,xN)T;Z为目标向量,z=(z1,z2,…,zN)T;δ为均值和方差分别为0、σ2的高斯白噪声,表示拟合误差;W为核函数的权重系数向量,w=(w1,w2,…,wN)T;K(x,xi)为核函数;Φ(x)为N×N+1的核函数矩阵。

由式(11)可以看出:目标zi服从均值、方差分别为y(xi)、σ2的高斯分布。

由贝叶斯理论可得目标向量的似然函数为:

(12)

为了对未知参数w和σ2进行估计,一般利用最大似然函数法(此处笔者不再赘述)。

在获得相关向量后,常利用多项式模型或指数模型拟合相关向量,并外推拟合曲线至失效门限,以得到剩余寿命,而轴承退化往往满足指数退化趋势。故笔者利用双指数模型对轴承进行建模,其形式如下:

CV=ae(bt)+ce(dt)

(13)

式中:CV为轴承退化指标;t为时间;a,b,c,d为未知参数。

笔者采用最小二乘法优化拟合退化指标,求解4个未知参数。

此外,上述方法虽能达到轴承RUL预测的目的,但未考虑双指数拟合相关向量得到的拟合结果与真实的轴承退化轨迹之间的误差。

为了更加精确地预测轴承RUL,笔者将考虑拟合误差对预测结果的影响,并利用ARIMA模型(p,q均为2,d为1)预测拟合误差,将预测值作为误差修正项加入到双指数模型中。

3 轴承剩余寿命预测流程

笔者所提出的轴承RUL预测方法流程如图1所示。

图1 轴承寿命预测流程Fig.1 Bearing life prediction process

轴承RUL预测方法具体步骤如下:

步骤1。从轴承振动信号中提取时域特征(均方根、峭度、偏度、波峰因子、峰-峰值、方差)、频域特征(频率标准差、重心频率、均方根频率)、时-频域特征(一级小波能量、二级小波能量),将这11个特征组成特征矩阵,经GMM、JRD处理,并归一化得到CV;

步骤2。对检查时刻至当前时刻的CV数据进行相空间重构。重构形式如下:

(14)

式中:左边部分为特征矩阵;右边部分为目标向量;m为嵌入维度,设为2;C1,…,CN为进入退化阶段至当前时刻的CV值;N为数据长度;

步骤3。将式(14)输入RVM模型训练,得到相关向量;

步骤4。利用双指数模型拟合相关向量,获取双指数模型未知参数,同时求解拟合误差;

步骤5。外推双指数模型至失效门限,得到预测退化曲线;

步骤6。利用ARIMA模型迭代预测拟合误差,得到拟合误差预测曲线;

步骤7。将ARIMA预测误差曲线补充到步骤5的预测曲线中,得到误差修正曲线;

步骤8。计算剩余寿命。

4 实验验证

笔者采用FEMTO研究所PRONOSTIA实验台3种不同工况下的轴承加速寿命数据[17]作为RUL预测实验数据集。该数据集中,振动数据的采样频率为25.6 kHz,每10 s采集0.1 s数据,以2 560个数据点为1个样本[18-19]。

具体实验工况以及所选用的轴承振动数据设置如表1所示。

表1 实验台轴承加速寿命实验工况介绍Table 1 Introduction of experimental conditions of accelerated life of bearing on test bench

4.1 退化指标性能对比

为了突出该退化指标相比目前常见的退化指标的优势,笔者引入均方根(root mean square, RMS)、自组织映射—最小量化误差(self-organizing map-minimum quantifying error,SOM-MQE)[20]、均匀型权重JRD作为指标对比。

实验台中3种不同工况下,4种轴承退化的对比结果如图2所示。

图2 退化指标性能对比Fig.2 Performance comparison of degradation indicators

由图2(a)、图2(b)可知:RMS和SOM-MQE指标波动较大,存在异常波动的情况,且单调性较差,易发生误报。图2(c)为采用均匀型权值JRD构建的退化指标,用CV1表示,相较RMS、SOM-MQE较为平滑,受噪声干扰较小,但单调性不太理想。图2(d)表示笔者所提的指数型权值JRD构建的退化指标,用CV2表示,其相比CV1指标更加光滑。

为了进一步评价退化指标的优劣,笔者引入单调性评价指标[21],该值越大,表明健康指标单调性越好。

单调性评价结果如表2所示。

表2 指标单调性对比Table 2 Comparison of monotonicity of indicators

由表2可知,除轴承B1采用均匀型权值的CV1单调性最优以外,笔者所构建的CV2指标单调性要优于其余几个指标。

此外,笔者所引入的指数型权重即式(9)中,平滑因子λ会影响退化指标的性能。

笔者以轴承B1为例,分析其对指标单调性的影响,分析结果如图3所示。

图3 λ取值实验Fig.3 λ value experiment

图3(a)为λ取值(1,10]时的CV2退化曲线。

由图3(b)可知:随着λ取值增大,健康指标单调性逐渐上升并逐步稳定;当λ取值为6时,健康指标单调性最高。

因此,此处笔者将λ设置为6。

4.2 齿轮箱初始故障识别实验

为了验证改进JRD后所构建的退化指标能够有效识别风电机组传动系统的初始故障,笔者利用自主研发并已安装到山西某风电场的风电机组状态监测与故障诊断系统采集齿轮箱振动信号,在传动链的主轴承、齿轮箱高、低速轴轴承、发电机前后轴轴承等部位安装美国PCB公司振动传感器,利用采集仪采集振动数据。

现场数据采集平台如图4所示。

图4 齿轮箱振动数据采集平台Fig.4 Gear box vibration data acquisition platform

已知该风电场2#机组齿轮箱于2016年11月底发生故障,2017年3月中旬更换齿轮箱。数据采集仪采样频率为51.2 kHz,每次数据采集时长1.28 s,每个振动数据文件共计65 536个数据点。

笔者分别采集了健康振动数据和已知故障振动数据。其中,齿轮箱健康振动信号长度为65 536个,截取1 024个数据点为一个样本,健康状态样本个数为64个;同时,分别提取2个不同时刻的齿轮箱故障振动数据,每个对应时刻提取数据长度为65 536,同样截取1 024个数据点为一个样本,得到故障数据样本共计128个。

笔者应用改进JRD后所构建的退化指标对样本数据进行分析,所得到的结果如图5所示。

图5 风电机组齿轮箱故障退化曲线Fig.5 Fault degradation curve of wind turbine gearbox

由图5(a)可知:在第64个样本处退化指标发生变化,齿轮箱进入故障阶段。其中,未改进前CV1和笔者改进后CV2的单调性分别为0.010 5、0.670 2。由此可知,笔者所构造的健康指标能够准确识别初始故障,其指标更加平滑、单调性更好。同时,笔者采用截取初始故障点前后的振动信号数据,即图5(b)、图5(c)进行分析,发现振动信号幅值变大,进一步说明改进后的退化指标对初始故障较为敏感。

4.3 轴承剩余寿命预测

4.3.1 评价指标

在设定的检查时刻Tc,笔者将预测曲线第一次穿越设定的失效门限时所对应的时刻记为Tf,则剩余寿命L(Tc)定义如下:

L(Tc)=Tf-Tc

(15)

为了更加直观地验证方法的有效性及优势,笔者利用相对误差对其进行衡量。其表达式如下:

(16)

式中:L真(Tc),L预(Tc)为在设定检查时刻Tc处,实际的RUL与预测得到的RUL。

4.3.2 剩余寿命预测

此处,笔者以轴承B1为例进行预测。在检查时刻788处的预测结果如图6所示。

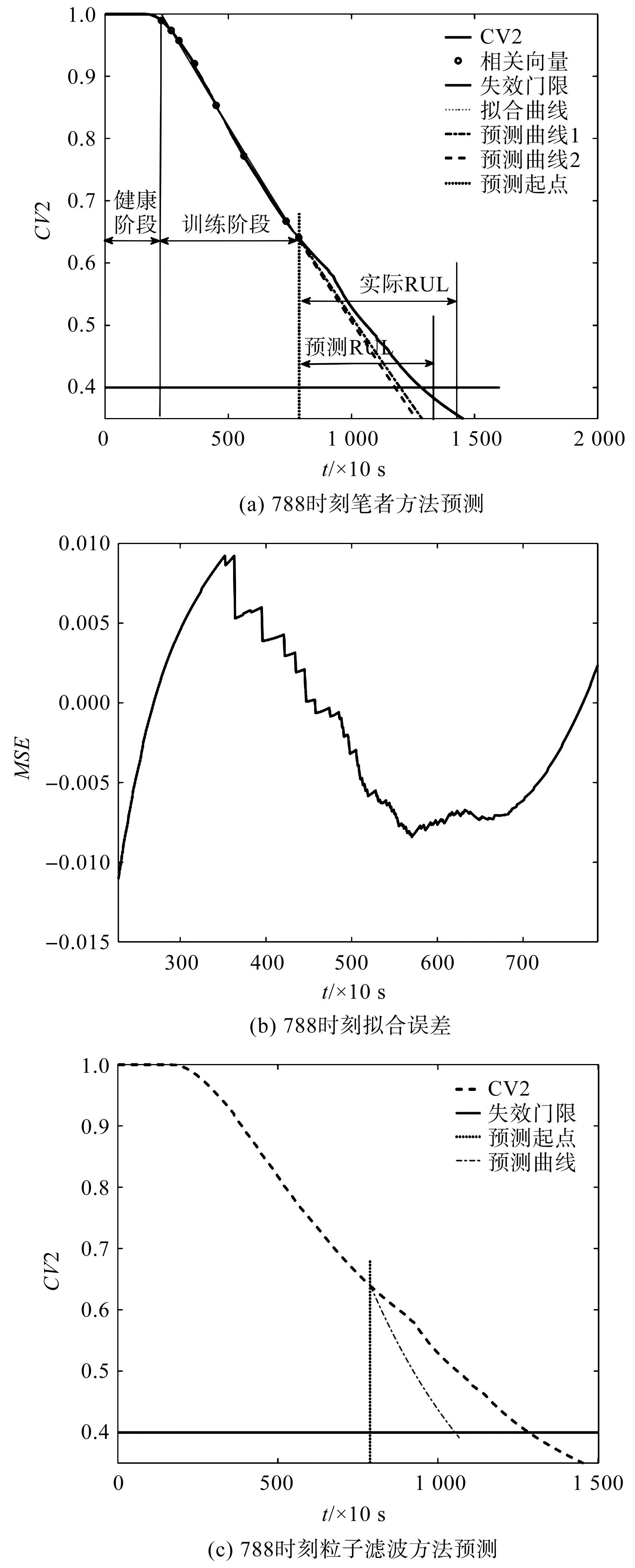
图6 轴承788时刻预测结果Fig.6 Prediction results of bearing 788 time

笔者对初始退化时刻至当前检查时刻CV2进行相空间重构作为RVM模型训练集,以得到相关向量,即图6(a)中圆圈所示;再利用双指数模型拟合相关向量,并外推双指数模型至失效门限得到预测曲线1,并计算拟合误差,即图6(b)所示;利用ARIMA模型进行误差修正得到的预测结果,即图6(a)中预测曲线2。

由图6(a)可计算得到788时刻的预测RUL为410(利用笔者所提方法),其中,实际RUL为494,相对预测误差(relative error,RE)为17.0%;而采用未经误差修正的方法所预测的轴承剩余寿命为391,相对误差为20.9%。

同时,笔者引入粒子滤波方法作为对比实验,其余时刻的预测结果如表3所示。

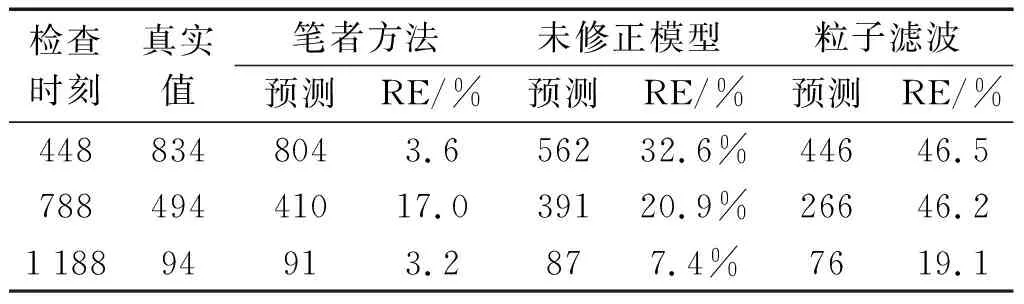
表3 轴承B1不同检查时刻预测结果Table 3 Prediction results of bearing B1 at different inspection times

由表3可知:相对于未进行误差修正及粒子滤波的方法,利用改进JRD及误差修正的双指数模型轴承RUL预测方法的预测精度更高,有较好的长期预测效果。

轴承B2在轴承退化阶段的前期、中期、后期的预测结果如表4所示。

表4 轴承B2不同检查时刻预测结果Table 4 Prediction results of bearing B2 at different inspection times

轴承B3在轴承退化阶段的前期、中期、后期的预测结果如表5所示。

表5 轴承B3不同检查时刻预测结果Table 5 Prediction results of bearing B3 at different inspection times

由表4、表5可知:在轴承退化的不同时刻,利用改进JRD及误差修正的双指数模型轴承RUL预测方法均能对轴承进行RUL预测。而在302时刻,由于B3轴承退化指标的非线性较强,给精准预测带来了一定的挑战。

总体而言,相比其他方法,利用改进JRD及误差修正的双指数模型轴承RUL预测方法的RE更小,预测精度更高。这有助于提高轴承的使用效率,降低维修成本。

5 结束语

笔者提出了一种利用改进JRD及误差修正的双指数模型轴承RUL预测方法,针对预测模型中未考虑拟合误差对寿命预测结果的影响,利用ARIMA模型对拟合误差进行迭代预测,作为预测结果的误差修正项,进一步提高了齿轮箱轴承的寿命预测精度;最后利用风电场数据与试验台数据对该方法的有效性和优越性进行了验证。

研究结果表明:

1)采用所构造的性能退化指标,可以对风电机组齿轮箱的初始故障进行准确识别;

2)相对未改进前的退化指标,经权值改进以后的退化指标单调性更好,退化指标的单调性提高了约14.3%,这可以提高后期轴承寿命预测的准确性;

3)利用ARIMA模型对拟合误差修正后,在不同检查时刻进行预测,结果的准确性都有不同程度的提高。

笔者为风电机组齿轮箱轴承剩余寿命预测提供了一种方法,为机组齿轮箱的预测性维护制定了计划。然而,该研究目前还存在一些不足之处,即在轴承实际性能退化的过程中,其失效阈值并不是固定不变的。因此,笔者下一步会将失效门限的动态化、区间化作为研究方向。