一种计算机模拟的针阔林木抗风性能分析

袁星月,方文杰,张怀清,安锋,云挺,4*

(1. 南京林业大学信息科学技术学院,南京 210037;2. 中国林业科学研究院,北京 100091; 3. 中国热带农业科学院橡胶研究所,海口 571101;4. 南京林业大学林草学院,南京 210037)

风是一种普遍存在的自然现象,树木与风之间常常发生复杂的相互作用。树木能够降低风速,防止水土流失,而强风能够对树木造成不可忽视的损害[1]。研究树木与风之间的相互作用,不仅能够评估台风对观赏树种与经济树种造成的损害,还有助于深入了解树林的防风效应,以优化防风林的结构。

树林与风的研究根据数据来源不同可以分为3类:卫星数据研究、实地实验与电脑模拟实验。通过对比分析台风袭击前后的森林卫星数据,能够对飓风造成的森林损害进行全面综合的评估分析[2]。实地实验要求研究人员前往风害发生频率较高的森林,等待自然疾风吹过或人工创造强风吹袭森林以采集数据[3]。风洞实验可以被视为一种模拟实地环境的实验方法,建造风洞放入移植的树木或人工树木模型,研究不同树林挡风效果背后的变化规律[4]。电脑模拟实验主要利用计算流体动力学(computational fluid dynamics,CFD),通过计算机模拟获得流体经过树木后的信息[5]。在电脑模拟实验中,往往将树木冠层看作均匀的多孔介质,通过调整模拟参数达到不同的模拟效果[6]。不研究树冠每片树叶状态的原因较多,一方面,当涉及整个树冠中几千片树叶时,仅仅是从树冠中分离出每片树叶这一步就较为复杂[7],而且每片树叶的状态也难以预测。单片树叶在风中可能呈现弯曲、扭转甚至卷曲等多种状态[8],防风效果又受树叶生长年限、叶柄刚度和叶柄长度等因素影响[9]。另一方面,一些风洞实验与多孔介质电脑模拟的组合实验已证实,多孔介质能够替代众多树叶进行符合现实情况的预测[10-11],故电脑模拟实验中常采用多孔介质模拟树冠。

总的来说,目前树木与风相互作用的研究已经能满足大部分环境下的需要,但依然存在值得深入研究的方向。一方面,依托自然环境进行的实验不可控、耗时长且有一定危险性;另一方面,现实中树木形态各异,单株树木内部的形态结构等表型特征难以使用数学方式描述和计算。

本研究首先仔细观察现实中的阔叶树与针叶树,总结它们各自的特点,进行了精细化建模;然后利用CFD技术,分别使用k-ε双方程模型和k-ω双方程模型进行多次模拟实验,模拟了阔叶树与针叶树附近的流场变化情况,记录总压力与风速数据;同时,多个截面也呈穿插状设立在阔叶模型与针叶模型中,记录局部的压力与速度数据,为后续的分析提供数据支持。该方法可控性强,能够形象展现不同树木附近的流场,分析不同树林在强风下内部气流状况,了解它们受气流影响与降低风速的程度,为研究不同树木与风之间的相互作用提供一种直观有效的方式。

1 试验方法

1.1 建立模型

根据阔叶树和针叶树形态结构,建立了两种树木模型。阔叶树模型参考的树木品种为樟树,属于南方常见的行道树,实际照片见图1a;针叶树模型参考的树木品种为黑松,也是广泛种植的优质观赏类针叶树,实际照片见图1d。最终构建的两种树木模型形态不同,但大小接近,高度均为10 m,且冠幅均接近6.3 m,能够较好表现两种树木的区别,展现不同树种的形态与其防风效应的关系。阔叶树模型由主干、分支及主干和分支对应的不规则叶团簇构成,针叶树由主干、分支及主干上附着的圆锥状叶团簇构成。将叶团簇视为整体,模拟成多孔介质[12]。

b和e分别为实地照片a和d对应的单株阔叶树与 单株针叶树模型;c和f分别为阔叶树林与附近流体域、 针叶树林与附近流体域的具体建模图。图1 阔叶树林与针叶树林的实地照片与具体建模图Fig. 1 Field photographs and concrete modeling images of broadleaf and coniferous forests

将9棵同种树木模型以6.5 m为间距排列为3×3的方阵,以分析不同树木组成的树林特点。阔叶树针叶树的实际照片和对应建模如图1所示。

模拟时,风从ZOX平面出发,向Y轴正方向流动。记9棵树中离ZOX平面最近的3棵树木为第1排树木,离ZOX平面较远和最远的两排树木分别为第2排和第3排树木。因为直面强风,第1排树木的状态可以作为现实森林中迎风面树木的参考。类似的,中间的1棵树(被其余8棵树包围)可以看成强风作用下森林中心树木的状况,第3排树木可以模拟森林背风面树木的状况。

1.2 湍流计算公式

湍流是流体的一种流动状态,流体的流动可以根据雷诺数的大小分为层流和湍流两种:层流指稳定且有序的流动,而湍流则是无规则、复杂的流动。雷诺数描述了流体在惯性力和黏性力之间的相对性,当流体速度较小、黏性较高时,雷诺数较小,流动趋向于层流,反之则接近湍流。

本试验主要研究强风状态下风树的相互作用,设定的风速高达30 m/s。高速流场中以湍流为主,几乎不出现层流,所以只考虑湍流,选择雷诺时均方程(Reynolds averaged navier stokes equations,RANS)模拟湍流相关参数,即重点关注一段时间内流体的平均流动状态。雷诺时均方程是对纳维-斯托克斯方程(navier stokes equations,NS)的改进,广义上纳维-斯托克斯方程由三大守恒控制方程组成,即质量守恒方程、动量守恒方程和能量守恒方程。常温空气作为一种不可压缩流体,流动时热量变化很小,通常不考虑能量方程。雷诺时均方程中的质量守恒方程和动量守恒方程由公式(1)和公式(2)描述[13]:

(1)

(2)

式中:ui(或uj)为xi(或xj)下的速度;i和j分别指空间直角坐标系的任意两个坐标轴的方向(i,j=1,2,3);t为时间;P为压力;ρ为空气密度。公式(2)中用到了一种简化数学表达的约定——爱因斯坦求和约定(Einstein summation convention),即使用一个项中的重复指标代表对指标的所有可能值求和[14],使得公式(2)实际包含了3个对应不同方向的公式。公式(2)中的有效运动涡流黏度νeff和关于阻力系数的附加项Fd由公式(3)和公式(4)计算。

(3)

(4)

式中:ν为动力黏度;νt为湍流运动黏度;k为湍流动能;ε为耗散速率;Cμ=0.09为经验常数;Cdf为阻力系数;a为叶面积密度(leaf area density,LAD),单位体积的总植物叶面积,m2/m3。阻力系数Cdf与a有关,使用收集到的N个样本数据[2]进行拟合可得到拟合函数。

前人针对阻力系数的研究表明,阻力系数随叶面积密度上升呈现先上升后平缓的趋势,单纯使用多项式拟合结果较差,所以选取以自然常数为底数的指数函数为拟合函数,该函数具有渐近线,符合阻力系数与叶面积密度的基本趋势。设f(a)为拟合函数,则有Cdf-f(a)为误差函数,使误差平方和s最小化。

对s运用多元微分法[15]使其最小化,即要求s各参数的偏导等于0,得到方程组:

(5)

(6)

(7)

求解该方程组,得到该方程的最优m0、m1、m2、m3、m4和m5分别为0.597 1,-1.235 0,1.712 0,3.943 0,-0.512 5,1.893 0。阻力系数Cdf与叶面积密度的最终拟合函数为:

(8)

阻力系数Cdf随叶面积密度a的增大而增大,当达到0.6后阻力系数基本保持不变(图2)。不同树种的叶面积密度不同,即使同为针叶树,柏树和松树的叶面积密度也有不同[16],分别为2.2和0.4 m2/m3。研究表明,同种阔叶树,杨树在不同栽培策略下的叶面积密度会在6～10 m2/m3波动[3]。综合考虑,本研究使用了1,5和10 m2/m33个不同叶面积密度,对应的阻力系数Cdf分别为0.53,0.60 和0.60。

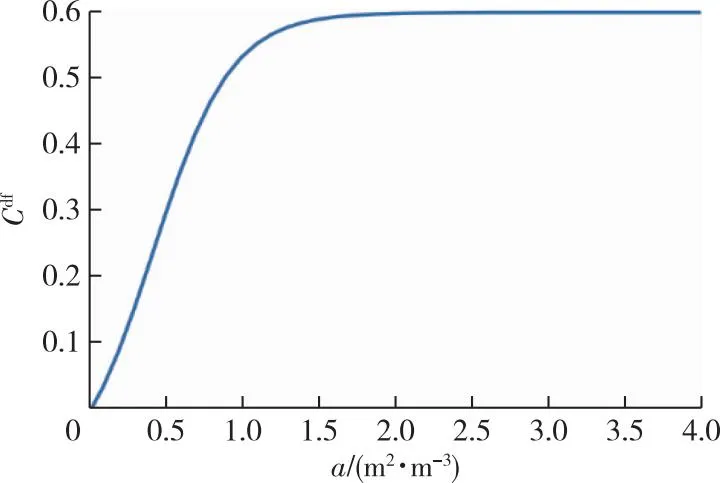
图2 阻力系数与叶面积密度的拟合函数曲线Fig. 2 Fitted function plot of drag coefficient and leaf area density

雷诺时均方程中的湍流运动黏度,即式(3)中的νt无法直接计算,需要引入湍流模型进行求解。湍流运动黏度可由k和ε共同推导,共使用到k-ε双方程模型和k-ω双方程模型两种湍流模型,都是针对树木冠层改进过的[5]。k-ε双方程模型是目前应用最广泛的湍流模型,能较好地模拟计算湍流的发展状况;k-ω双方程模型中,ω是比湍流耗散率,该湍流方程更加注重边界层的细节,同时需要更多计算资源。本研究主要使用k-ε双方程模型,在使用到k-ω双方程模型时会额外指出。

本研究使用的k方程和ε方程增加了与树冠相关的附加项,具体的k方程和ε方程如公式(9)和公式(10)所示[13]:

(9)

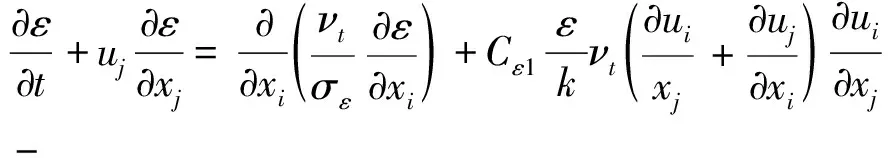
(10)

式中:经验常数Cε1=1.42,Cε2=1.92;常数σk=1.0,σε=1.3;Sk和Sε分别是k方程和ε方程中与树冠相关的附加项。流体穿过类似树冠的多孔介质时,发生了尾流产生和能量减少两种现象,故k方程附加项Sk等于尾流产生项Pk和能量损失项Lk之和。

Sk=Pk+Lk

(11)

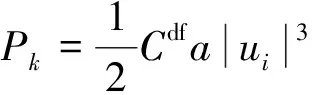
(12)

Lk=-2Cdfa|ui|k

(13)

耗散速率ε可以表示成湍流动能k的函数关系式:

(14)

式中:Cε=0.16,为经验常数;l为混合长度。若l取为定值,则公式(14)两边对k求导变形可得到k和ε的具体数值关系,如公式(15)所示:

(15)

k方程附加项Sk,即公式(11～13),可与公式(15)的最终形式联系起来,得到公式(10)中所示ε方程附加项Sε:

(16)

但l的大小会因为方程计算对象所处位置的变化而改变,公式(16)具有一定的局限性,故研究人员[13]通过研究使用经验系数修正了ε方程附加项Sε:

Sε=Pε+Lε

(17)

(18)

Lε=-4Cpε2Cdfa|ui|ε

(19)

式中,Cpε1=1.8,Cpε2=0.6,均为经验常数。

关于k-ω双方程模型,k方程与k-ε双方程模型相同,ω方程见公式(20):

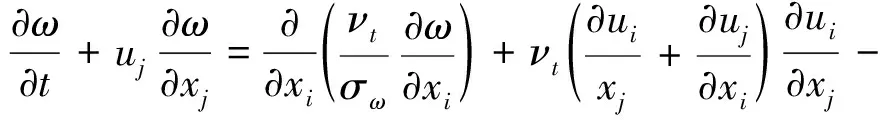
(20)

常数σω=0.5,ω方程中对应的与树冠相关的附加项Sω见公式(21):

(21)

树冠相关的附加项Fd只在冠层内部存在,在冠层之外的流场域中本节的各附加项都记为0:

Fd=Sk=Sε=Sω=0

(22)

不同研究往往在附加项上进行研究与变动以完成针对树冠的改进与优化,本研究提及的Fd、Sk、Sε和Sω4个附加项与树冠参数密切相关,属于对原始雷诺时均方程的重要改进,在树冠模拟实验中有着重要作用。

1.3 网格化

网格化指将原来连续的求解区域划分一系列不重复的有限单元[17],是对空间的离散化,便于下一步迭代求解。采用单元质量用于表现网格划分质量,单元质量越大越好,一般不能低于0.7。阔叶林单元总数为4 176 642,平均单元质量为0.834 54;针叶林单元总数为14 071 152,平均单元质量为0.838 66。具体网格如图3所示。

图3 阔叶树林与针叶树林的网格图Fig. 3 Meshing images of broadleaf forest versus coniferous forest

1.4 龙格-库塔法

龙格-库塔法是求解微分方程的一种常见数值解法[18],在工程上应用广泛[19]。与解析解相对,数值解指通过使用数值计算方法对问题进行近似求解得到结果[20]。解析解的运算耗时极长,还存在无法通过数学分析获得解析解的情况,所以数值解使用广泛,对湍流模拟有重要意义。

四阶龙格库塔法作为高阶龙格-库塔法,具有高精度、低误差的优点。以k-ε湍流模型为例,式(1)、(2)、(9)和(10)共同构成了关于湍流求解的微分方程组,运用四阶龙格-库塔法,对微分方程组进行求解。需要求解的微分方程和已知的初值简化如公式(23)所示:

(23)

式中:A表示空间x、时间t中任意一个变量;B表示压力P、速度u、动能k和耗散率ε中任意一个变量;c1和c2为对应的初始值,整个微分方程中初始值是完全已知的。f为解关于湍流的微分方程组得到的关于B的一阶导数:

(24)

龙格-库塔法属于迭代法,以一次迭代为例,第n+1次迭代中,需要将第n次迭代中的已知数据Bn代入公式(25):

(25)

则可得到下一个迭代的Bn+1值,该值是由Bn加上步长和估算斜率的乘积得到的。K1、K2、K3和K4分别是用于计算估算斜率的开始斜率、两个中间斜率和终点斜率。当对时间偏导时,λ作为时间间隔,是人为选取的;对空间偏导时,λ由网格给出。公式(24)是由4个方程构成的方程组,其中前3个方程分别是速度、动能和耗散率关于时间的偏导。它们代入公式(25)后,具体方程见公式(26)～(28)。

(26)

(27)

(28)

已知所有网格的压力初始值,在求得某一个网格下一个迭代的新压力数值后,可以通过推导计算出附近网格的压力值,进而得知所有网格的新压力值,以此不断迭代得到收敛解[21]。

对单个网格而言,求得速度后,求解压力需要对公式(24)方程组最后一个公式求偏导,可得到压力泊松(Poisson)方程[22]见公式(29),推出下一迭代的压力值:

(29)

每次迭代中各变量会进行计算得到更新。重复迭代,当某一循环下同一网格的压力变化与上一循环相比小于0.1%或迭代循环次数达到300时,即退出循环。可得到任意时空下的压力P、速度u、动能k和耗散率ε数值。

2 结果与分析

根据GB/T 28591—2012《风力等级》,12级风被定义为台风,又称一级飓风,风速区间为32.7～37.0 m/s。本研究将入口风速设置为30 m/s,两种树木模型与3种叶面积密度组合进行6次实验。

2.1 压力分析

阔叶林与针叶林不同叶面积密度下的总压力剖面云图见图4。图4中每个分图都包含10个压力剖面云图,这些半透明剖面以3.25 m为间距排列,贯穿整个树林。

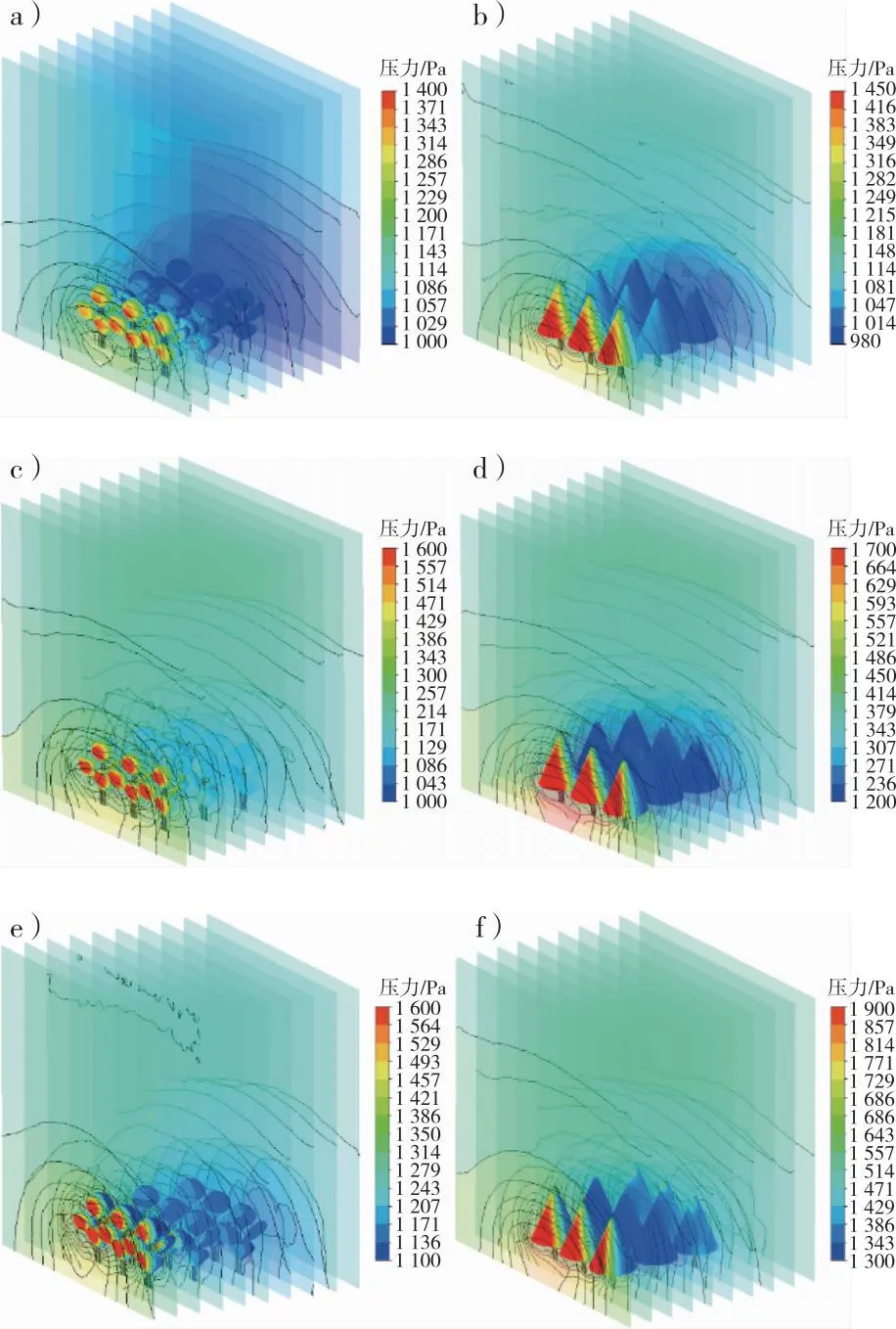
a～c)分别是叶面积密度为1,5和10 m2/m3的阔叶林结果; d～f)分别是叶面积密度为1,5 和10 m2/m3的针叶林结果。图4 阔叶林与针叶林不同叶面积密度下的总压力剖面云图Fig. 4 Total pressure profile cloud at different leaf area densities of broadleaf forest and coniferous forest

总体来看,不同叶面积密度下,阔叶林与针叶林附近的气流压力变化趋势类似。压力极大值区域的出现位置都为迎风面第一排树的前方,大范围低压区都出现在了树林后方。遇到物体阻碍后,气流在物体前方产生高压区,在物体后方产生低压区,整体来看对物体施加与流动方向同向的力。

随着叶面积密度的上升,最前排树木承受的压力不断增大,树林内部的气压差也不断上升。面临同等强风,枝叶稀疏的树木比枝叶茂密的树木承受的压力更小,不容易受损。强风吹落大量树叶后,树木整体状态会趋于稳定。

为了更好地展示不同位置的压力情况,从图4每个分图中单独取出了4个剖面,分别是迎风面第1排树木前的剖面1(距第1排树主干3.25 m),第1排树木和第2排树木之间的剖面2(距第1排和第2排树主干均为3.25 m),第2排树木和第3排树木之间的剖面3以及第3排树木后面的剖面4(距第3排树主干3.25 m)。以叶密度最高的阔叶树林为例,4个剖面的位置示意图见图5a,不同树木模型中四剖面的位置相同。从下风侧观测图5a所示四剖面的压力云图,不同实验的压力剖面图如图6所示。

图5 剖面位置和测量风速位置的示意图Fig. 5 Schematic diagram of the sections and the measured wind speed position

a～c)叶面积密度为1,5和10 m2/m3的阔叶林结果;d～f)叶面积密度为1,5和10 m2/m3的针叶林结果。 1、2、3和4分别对应剖面1、剖面2、剖面3和剖面4。图6 阔叶林与针叶林不同叶面积密度下的4个压力剖面Fig. 6 Four pressure profiles at different leaf area densities in broadleaf and coniferous forests

从左到右观察图6,压力剖面1中间压力大周围压力小,后3个压力剖面中间压力小周围压力大。剖面4展现的高压力区域边界与树木树冠本身的形态边界类似,阔叶树为不规则圆状而针叶树是上小下大的箭头状,说明压力的产生区域与承受流体的多孔介质形态有一定的关联。在形状相似的单树构成的树林中,树林边缘的树木承受的压力低于树林内部的树木,更易受损。这一特点在图6e3中表现最为明显,树林边缘的树木附近压力仅为1 210 Pa,树林内部的树木附近压力达到1 234 Pa。

为了进一步分析,选择最高叶面积密度的阔叶树林中的压力剖面3,即图6c3对应的情况,进行k-ω湍流模型模拟,阔叶树林两种湍流模型的剖面3压力云图对比结果见图7。

图7 阔叶树林在不同湍流模型下剖面3的压力云图对比Fig. 7 Comparison of pressure cloud image in Section 3 of broad-leaved forest under different turbulence models

图7中两张分图的压力上下限及压力分布类似,图7b捕捉到了更多细节。图7b的低压区面积比图7a更大,整个剖面的压力上下限也更大,证实了k-ω湍流模型对边界的细节处理更优秀。

综合统计模型总体数据与4个剖面数据,可以得到表1所示的各区域压力数据。

不同叶面积指数的针叶林平均总模型压力极大值(2 112.70 Pa)大于阔叶林(1 898.73 Pa),在针叶模型树冠边角处易产生局部高压区。阔叶林总模型整体压力差大于针叶林,阔叶林内部气流比针叶林更混乱,抗风能力较弱,这可能跟阔叶树树冠体积较大有关;分析表1数据可以发现,各剖面的压力极值没有负压,而总模型存在负压。压力为负值表明压力低于参考压力,该区域产生了吸力,附近的枝干与叶团簇更容易受损。总模型负压区集中在树干后方极小区域,该区域压力急剧下降,和现实中树木在强力风荷载下枝条易弯折的情况是吻合的。最后观察各剖面之间的联系:相比其他剖面,剖面1有最高的平均压力极大值(1 690.91 Pa)、最高的平均压力极小值(1 283.96 Pa)和最大的平均压力差(406.95 Pa)。后几个剖面的压力极值和压力差与剖面1相比均有下降且后几个剖面的数值较为接近,说明当狂风来袭时树林迎风面第一排树木承受了最大的压力。

表1 CFD模拟中的各区域压力数据Table 1 Regional pressure data in CFD simulation

2.2 树林内部风速分析

阔叶林与针叶林风速矢量图见图8。图8最后一排树木的枝干处和树林后方均出现细小的蓝色箭头,表现了风速的降低。黄色箭头聚集在整体树林的四周,即树林底部、侧面与树林树冠上方的风速都有提升,这是一种基础的流动情况[23]。当流体绕过物体流动时,因为存在物体的阻碍,流体的流通面积变小了,所以在物体侧面,流体需要以更快的速度通过,才能保证和上游流通能力相同。

图8 阔叶林与针叶林速度矢量图Fig. 8 Broadleaf and coniferous forest velocity vector plots

矢量图也展现了阔叶树和针叶树的区别。由于树冠结构不同,气流经过针叶树树冠顶部尖端受到的影响更为突出。远离树冠的地方风速高,越靠近树冠风速越低。阔叶树树冠由多个叶团簇组合而成,且不同叶团簇之间有空隙,所以在叶团簇之间,气流的影响非常明显,迎风面第1排阔叶树的叶团簇之间有大量黄绿色较高速的矢量箭头,表明阔叶林内部风速分布相对不均匀,波动大。

在图5a所示四剖面的位置再次设置4个风速剖面用以采集风速数据,不同叶面积密度下不同模型不同位置的对应风速数据见表2。

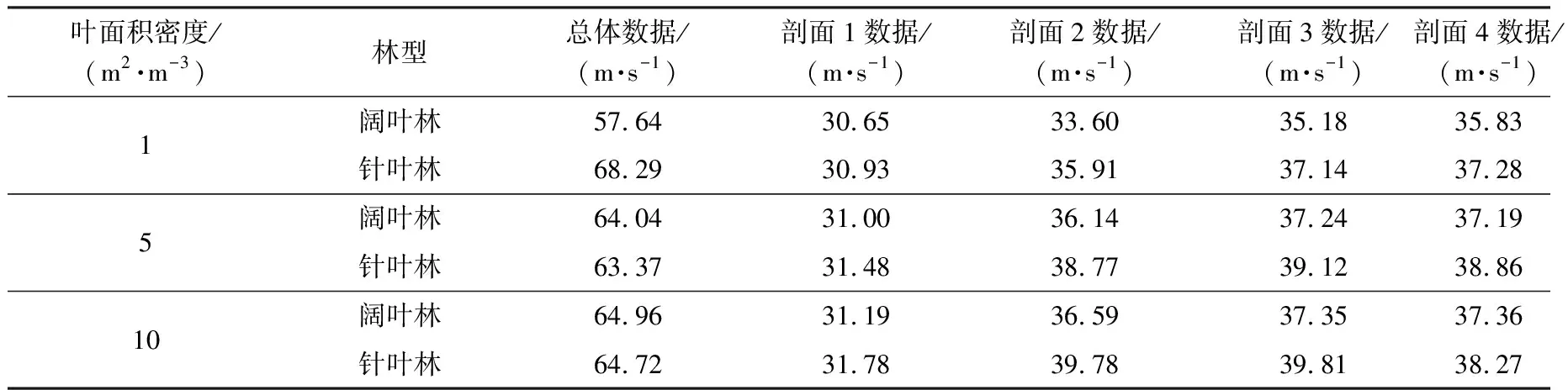
表2 CFD模拟中的各区域最高风速数据Table 2 Maximum speed data for each region in CFD simulation

总模型中最大风速出现在第1排树的树干附近。第1排树的树干直接暴露在强风中,因此在它们附近出现了高风速区。而由于树木的阻碍作用,各剖面的最大风速都出现在树林侧面和树冠上方。

2.3 下风侧风速垂直分布图分析

树木模型见图9a,在入口风速为30 m/s,叶面积密度为1,5和10 m2/m3时,两种树林模型在下风侧两个距离树林10 m(1倍树高)和20 m(2倍树高)的风速数据见图9b、c和d。纵坐标表示测量高度,横坐标表示测量高度对应的风速。两个测量风速的具体位置参见图5b中所对应的绿色和蓝色线位置。

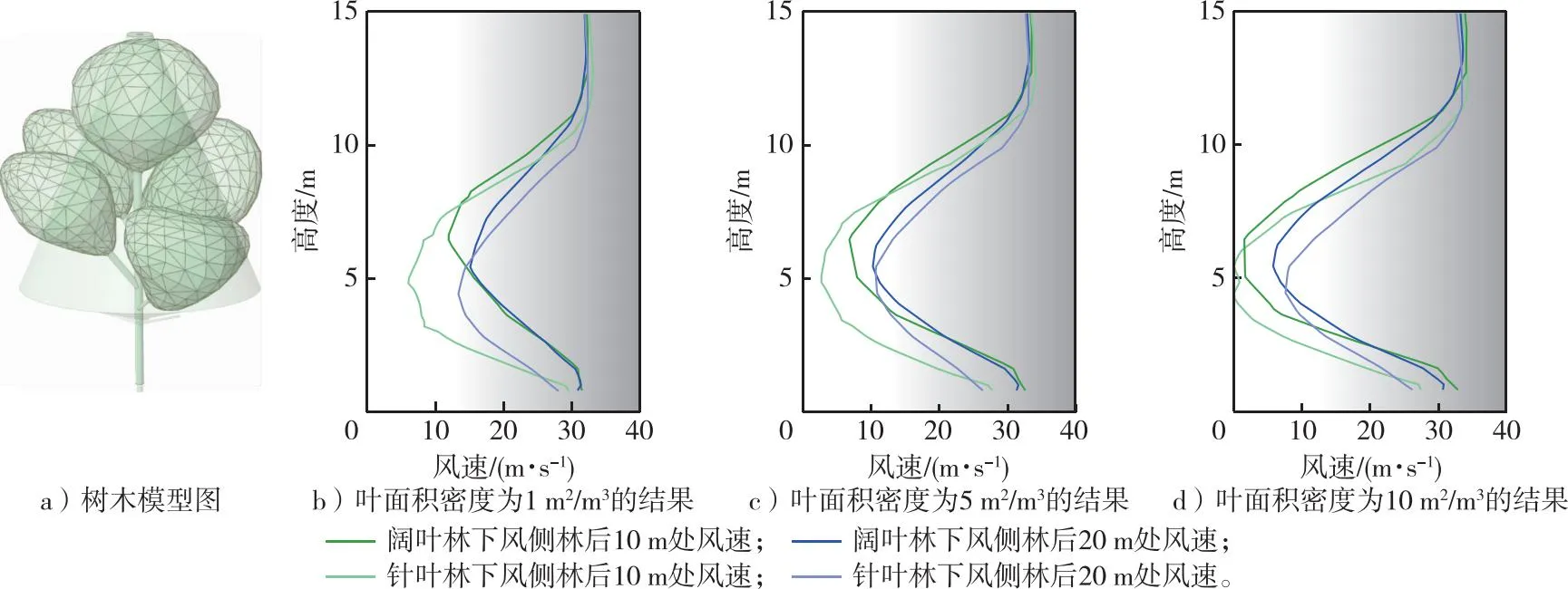
图9 下风侧风速垂直分布图Fig. 9 Vertical wind speed distribution on the leeward side

整体而言,图9中b、c和d 3个分图表明叶面积密度越大,树林挡风的效果越好,二者是非线性关系:高叶面积密度数值再次提升时,树林的挡风效果提升较小,趋于稳定。从具体数值来看,叶面积密度由1 m2/m3增加到5 m2/m3时,阔叶林针叶林下风侧10 m处最低风速平均下降4.43 m/s;而叶面积密度由5 m2/m3增加到10 m2/m3时,下风侧10 m处最低风速平均下降3.73 m/s,变化较小。

所有数据趋势相似:风在经过树木模型树冠层(高度2～10 m)附近时,速度明显降低。树冠层上方,风速逐渐上升又回到入口风速的30 m/s左右,13 m高度以上几乎看不到树木对风的影响。2～10 m是树木冠层的主要分布区,风速显著降低且离树林越近降低越多。12 m高度处风速略高于入口面的30 m/s风速,这是阻拦引起的加速现象。

风速在20 m测量点处的变化幅度小于10 m测量点处,并且树木模型的种类也影响风速的垂直分布。阔叶树整体冠层趋近于球状,而针叶树的树冠形态近似圆锥,冠层重心偏下。所以叶面积密度较低时(图9b),通过两种树木的风分别在约6和4 m高度处达到最低速度。但随着叶面积密度的上升,风速的极小值出现的高度都向5 m高度处移动,树木冠层的形态对树后气流的影响逐渐减弱。

3 结论与讨论

本研究建立了阔叶树和针叶树的树木模型,并保留了两种树木的形态特征,改变叶面积密度进行多次实验,定量分析比较不同条件下压力速度的分布情况。

本研究结论在两方面与现有实验方法的结果相似。首先在损伤性评价方面,模拟结果显示叶面积密度数值高的树木承受的压力更大,在风中的受损概率也比叶面积密度低的树木大,更易发生倒伏。说明阔叶林内部气流比针叶林内部气流混乱,阔叶林内部的局部最大风速大于针叶树内部,更易受损。考虑到同等树高和冠幅下,阔叶树的树冠体积大于针叶树,也就是说树木的形态特征可能是判断风损害树木程度的重要因素,树冠体积小的树木抗风性能优于树冠形态不规则且体积大的树木,更易发生枝干弯折与叶片脱落,这与华南地区及安徽农业大学风灾后实地统计数据相符[24-25]。

其次在挡风效果方面,下风侧风速垂直分布数据给出了定量的评价,不同叶面积密度下,各树林下风侧1倍树高的地方,最低风速与入口风速相比下降了60.13%～98.51%。Poh等[6]使用的实地测量数据显示,针叶树防风林下风侧1倍树高的地方最低风速下降了约60%,该实测数据在本研究模拟数据范围内。类似的风洞实验中,郑波等[26]使用定制的阔叶林模型与通用树林模型多次排列成不同树林测得各树林下风侧一倍树高的地方,最低风速与入口风速相比下降了68.5%～98.9%,与本研究模拟的上下限误差分别为8.37%和0.39%,这可能是不同实验环境中叶面积密度与树林行数不同导致的正常波动。在改变叶面积密度的风洞实验中,Cao等[4]对同一树木逐步摘除叶片后进行多组风洞实验,得到的数据显示:叶面积密度越大,树木挡风效果越好,但树木挡风效果增加到一定程度后,再提升叶面积密度,挡风效果改善变缓,与本研究实验结论呈现一致的趋势。

本研究方法具有如下优点:首先,电脑模拟实验绕过了测速器材的限制,能够得到树林中每个角落的详细数据;其次,入口风速灵活可控,能够为实验创造出适合的环境,降低时间和资金投入。最后,树木模型体现了阔叶树的分支结构和针叶树的树冠形态,能够较好地展现树林内部的气流状态。本次实验验证了k-ε湍流模型和k-ω湍流模型的差异性,产生了不同叶面积密度下的多组压力速度数据,为树木在风力作用下的行为提供了数据支持。这些结果能够帮助进一步深入研究树木风力响应的机制,推测树木的结构变化和振动特性,对于优化数值模拟方法以及应用于实际工程和环境中也具有重要意义。

本方法也存在一些可进一步优化的方向:树木模型还有细化的空间,可以尝试构建得更精细;研究对象都是由同种树木构成的纯林,可以扩展到针叶混交林或更为复杂的森林模型,将灌木等低矮树种纳入模型;通过引用更贴合实例的叶面积密度数据开展更有针对性的研究。

研究树木在强风作用下的各类参数在防护林、绿化带等设施的构建中有指导意义。本研究基于雷诺时均方程、改进的k-ε湍流模型和k-ω湍流模型,采用CFD模拟,研究了不同叶面积密度下不同树木模型的抗风表现。结果表明,叶面积密度对树林阻风效果的影响大于树木模型对树林阻风效果的影响。随着叶面积密度的增大,树林阻风效果不断增强。叶面积密度由1 m2/m3增加到5 m2/m3时,下风侧10 m处阔叶树风速的最大下降百分比由60.13% 提高到77.70%,针叶树由79.50%提高到91.36%。针叶树的挡风能力强于阔叶树,同在下风侧10 m处且叶面积密度同为1 m2/m3时,针叶林的最低风速为阔叶林最低风速的51.43%。本研究使用的方法可以通过调整参数与建模,扩展细分到不同种类的阔叶林与针叶林;结果可用于分析确定森林在大风条件下的各类参数,预测强风袭击后树木的损毁情况,对不同森林种植策略下的风损害进行量化分析。同时可以帮助建设更合理的防风林,有利于更好地节省资金,在强风下保护设施。