基于改进粒子群算法的木材板材下料方法
黄秀玲,陶泽,尤华政,李宸,刘俊
(南京林业大学机械电子工程学院,南京 210037)
在家具行业中,以绿色环保、节约能源为目的的优化木材板材下料问题已经成为研究热点,木材板材下料问题受重视程度日益提高。目前有很多企业生产家具产品时,对于木材板材仍使用人工下料,经常耗时较长且材料浪费严重。由于客户需求的多样性,需要合理安排下料方案,充分利用木材板材,提高企业经济效益和节约社会资源。本研究的木材板材下料优化问题属于二维矩形下料问题,是一种具有高度计算复杂性的问题[1-4]。
20世纪60年代,Gilmore等[5-6]提出了经典的“一刀切(guillotine cutting)”和“正交切割(non-guillotine cutting)”两种二维切割方式,通过线性规划和动态规划,解决了“一刀切(guillotine cutting)”问题范围内的下料算法,首次为解决下料问题提供了切实可行的方案和技术手段。但是由于当时计算辅助技术并不是很突出,所以仅停留在理论层面。
20世纪90年代后期,随着计算机技术的高速发展,计算复杂性理论不断成熟,大量的智能优化算法不断涌现,并在各行业中得到广泛应用[7-8],如遗传算法(genetic algorithm)、模拟退火算法(simulated annealing)、灰狼优化(grey wolf optimization)、蜻蜓算法(dragonfly algorithm)、蚁群算法(ant colony algorithm)以及粒子群算法(particle swarm optimization algorithm)等。这些算法一般都是建立在生物智能或物理现象基础上的随机搜索算法,可以解决大规模的复杂下料问题,且通用性较强[9-11]。笔者主要针对单规格木材板材下料问题,在木材板材长和宽都大于零件长和宽的情况下,采用粒子群算法、变邻域搜索算法、粒子群变邻域搜索混合算法求解单规格木材板材下料问题,并进行分析对比。
1 数学模型的建立
本研究所采用的原材料板材为L×W的矩形木材板材,待切割的毛坯零件一共有K种。在充分考虑多方面因素和约束的前提下,选择以剩余废料最少为优化目的,得出数学模型如下[12]:
0≤Xk≤L,(1≤k≤Cj,1≤j≤N)
(1)
0≤Yk≤W,(1≤k≤Cj,1≤j≤N)
(2)
(3)
(4)
Rk∩Rkj=∅,(1≤k≠kj≤Cj,1≤j≤N)
(5)
(6)
(7)
Tj≥1,(1≤j≤N)
(8)
(9)
式中:L和W分别为原材料板材的长度和宽度;l和w分别为零件板材的长度和宽度;i和K分别为零件类型编号和集合,i∈K;N为原材料板材的数量;Cj为j张单板上排放零件数量;(Xk,Yk)为每个矩形零件对应左下角的坐标,k∈Cj;Pk为矩形零件在原材料中的排列方式;Rk为零件所在矩形的命名;ni为第i类零件的数量;Aij为在第j张单板方案中第i种零件的数量,且Aij≤ni;Tj为第j种方式的切割次数,j∈N,Tj≥1;F为目标函数。
式(1)确保排放在原材料板材上的所有毛坯零件X轴上的长度不会超出原材料板材的长度;式(2)确保排放在原材料板材上的所有毛坯零件Y轴上的长度不会超出原材料板材的长度;式(3)和式(4)为了保证零件不会超出原材料板材的边界,限制了长度和宽度;式(5)保证毛坯零件不会重叠排放在原材料板材上;式(6)和式(7)使所有毛坯零件的数量和配套要求得到满足;式(9)是目标函数,使得浪费的原材料板材的面积最小,也就是保证原材料板材的利用率能够达到最高。
2 算法求解
2.1 粒子群算法
粒子群算法也称作粒子群优化算法(particle swarm optimization,PSO),是1995年美国Kennedy等[13]通过对鸟类群体行为进行模仿提出的一种进化算法(evolutionary algorithm,EA)。粒子群算法通常用于解决连续优化问题,将其应用于排样问题中的排列组合问题,需要对粒子群算法进行一定的调整[14-15]。
2.1.1 编 码
排列组合问题涉及对元素进行排列或组合,因此需要定义适合该问题的编码方式。常用的离散式编码方法主要包括二进制编码、排列编码或One-Hot编码等方式。针对排样问题的顺序优化上选用基于位置的编码方式,即将每个可行解看作一个由各个元素位置决定的序列。排样过程中每个可行解可以表示为一个由n个元素位置决定的序列,其中第i个元素表示该物品在排样中的位置,具体的零件排序方式为:
X=(x1,x2,…,xi-1,xi,xi+1,…,xn)
(10)
式中:xi表示第i个零件在排样中的位置,i=1,2,…,n。整个序列X表示优化过程中一个完整的零件排列[16]。这样的编码方式可以保证每个粒子的取值范围是固定的、不重复的,且可以直接映射到可行解的空间。
2.1.2 粒子速度
在排列优化问题中,由于粒子编码格式的特殊性,速度与位置的运算方式需要重新定义。本研究采用基于位置编码方式的离散式粒子群算法速度的计算方式[17]。
定义速度V为位置X2和位置X1的差值,是一个N维向量:
V=X2-X1
(11)
式中,速度V中的每个元素vi表示为X2和X1在序列上对应的元素的对比。当X1的元素与X2相同时速度V上的元素记录为0,当X1的元素与X2不相同时速度V上的元素记录为X2的元素,具体可表示为:
(12)
排列优化问题中,位置与速度的加法运算可表示为:
X=X1+V1
(13)
式中,进行加法运算后新产生的向量的每一个分量以序列i的顺序按照以下方式计算:当V1的元素为0时,X的元素记录为X1的元素;当V1的元素不为0时,X的元素记录为V1的元素,并将X1中对应数值x1,i与数值v1,i的序列位置交换(由于编码的方式为位置编码,对于任意序列X1,当x1,i与v1,i不同时,X1中都应包含非零元素v1,i)。具体可表示为:
(14)
粒子的运动方程具体描述如下:
V=c1(Xpbest-X)+c2(Xgbest-X)
(15)
式中,速度的数乘方式具有概率意义,它可以增强计算的随机性。在计算过程中生成一个随机数,通过数值的比较确定速度值。
(16)
2.1.3 目标函数
矩形排样问题的目标是在一个给定规格的矩形板材上,按照某种排列顺序摆放零件,从而最大化板材的利用率。在粒子群算法中,将编码数值作为排样顺序,将位置编码下产生的排样利用率作为目标。
具体的,粒子群算法下,排样策略的全局目标如式(17)所示:
(17)
式中:f表示为下料零件总面积在所用板材面积中占据的最大比例;i为零件序号;N为零件总数;Si为第i个零件所占据面积;W为板材宽度;H*为该排样方案下N个零件排放完毕后,零件排样图的最大使用高度。
2.1.4 粒子群算法流程
本研究粒子群算法的流程如图1所示,具体流程如下:
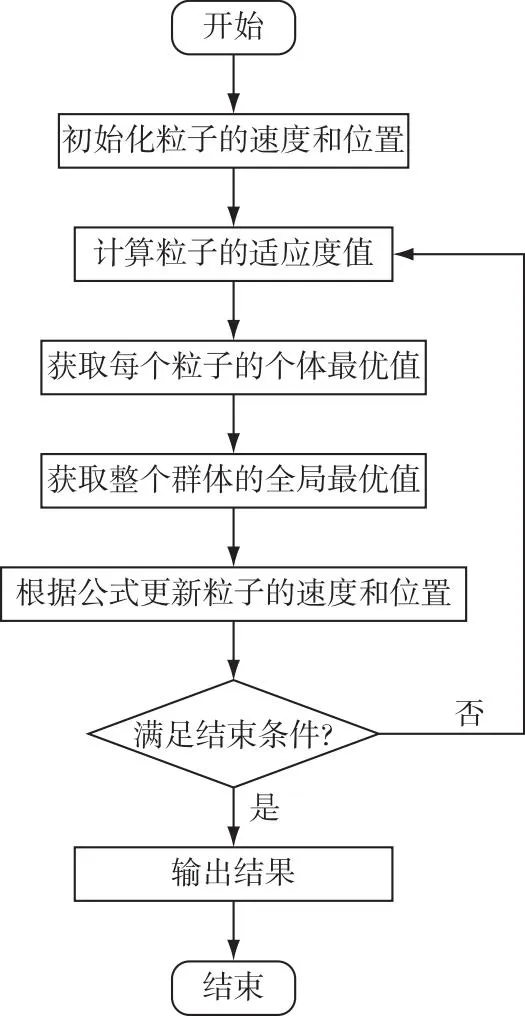
图1 粒子群算法流程Fig. 1 Flow chart of particle swarm optimization
1)粒子群状态进行重置。
2)对粒子的适应度值Fit[i]进行计算。
3)个体极值pbest(i)比较,当Fit[i]>pbest(i)时,Fit[i]替换掉pbest(i)。
4)全局极值gbest(i)比较,当Fit [i]>gbest(i)时,Fit [i]替换掉gbest(i)。
5)根据式(13)和式(15)更新粒子的位置Xi和速度Vi。
6)判断是否满足结束条件(误差足够好或者达到最大循环次数),若满足,则算法结束并输出最优结果;若不满足,则返回2)。
2.2 变邻域搜索算法
变邻域搜索算法(variable neighborhood search,VNS)是由Hansen和Mladenovi在1997年提出的一种新颖且高效的局部搜索算法[18-19]。其基本思想是:为了能够更好地获取局部最优解,算法扩展了解的搜索范围,并且在搜索的过程中系统化地改变其多个邻域结构[20-21]。
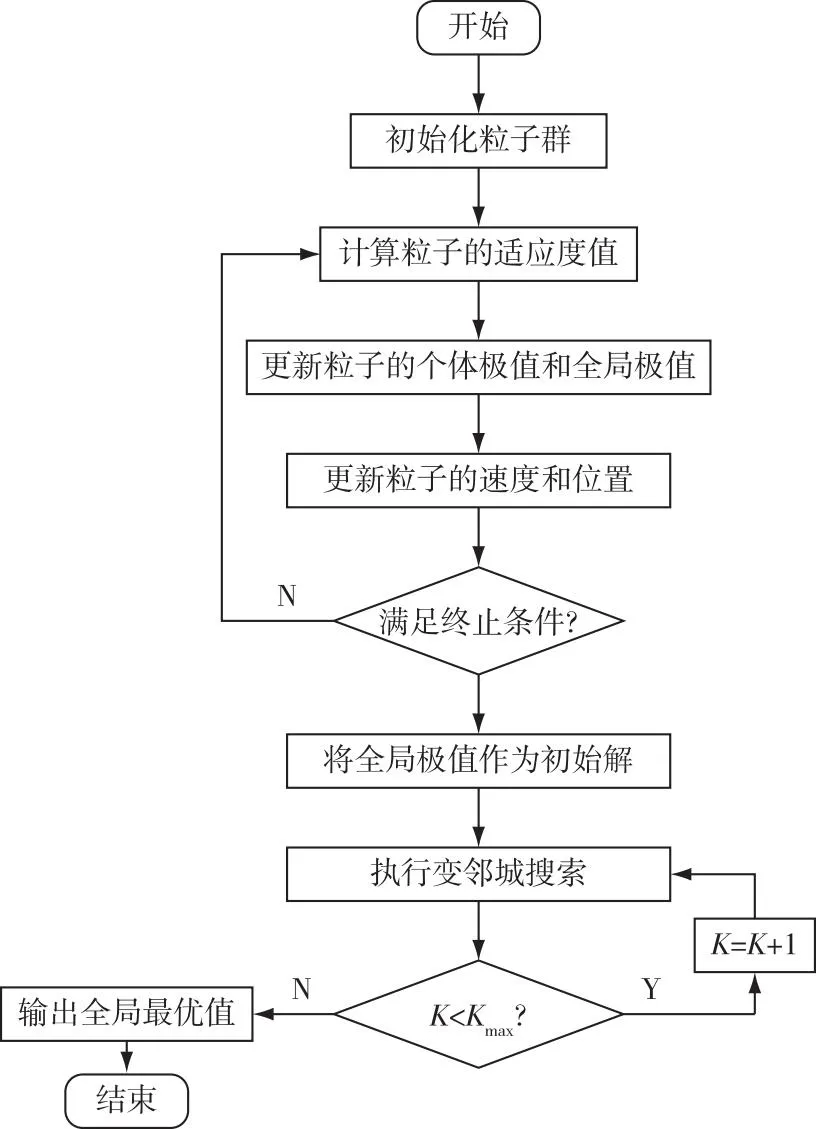
本研究变邻域搜索算法的简要流程如图2所示,算法流程如下:
1)初始化。给定一个初始解S,并定义一系列邻域结构NK,K=1,2,…,Kmax。
2)令K=1。
3)把定义的初始解S作为当前解,在当前邻域NK内进行局部搜索获得该邻域的最优解S1。
4)若S1优于S,就用S1替换掉当前解S,跳回2);若不优于S,就令K=K+1。
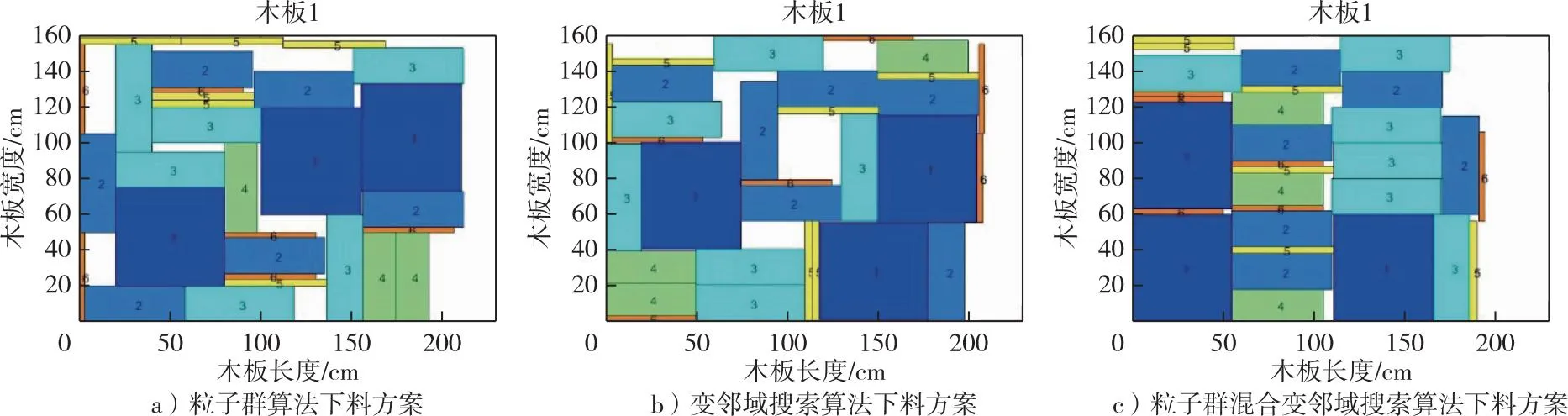
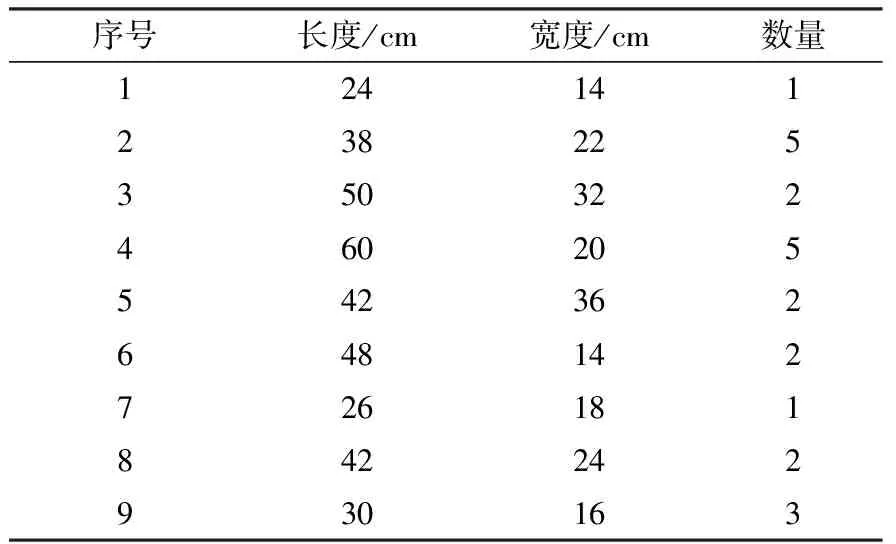
5)若K>Kmax,就直接输出最优解,结束;若K 图2 VNS算法流程Fig. 2 Flow chart of VNS algorithm 变邻域搜索主要包括局部搜索(local search)和改变邻域(neighborhood change)。其中,局部搜索的作用是在同一个邻域结构中寻找更优的局部最优解,改变邻域的作用是为整个搜索过程提供一种迭代方法和停止准则。 本研究根据排样需要采用混合性邻域结构的变邻域搜索策略[22]。其基本步骤如下: 1)初始化。选择初始解x,邻域结构N(i),i=1,2,…,k,当前最优解xbest=x。 2)如果满足算法终止条件,那就输出xbest;若不满足算法终止条件,那就令i=1。 3)如果i=k+1,那么就跳转步骤2);否则,在x的邻域结构N(i)中随机选取可行解x′,在x′的邻域结构中搜索得到局部最优解x″,若x″比当前最优解xbest更优,则xbest=x″,i=i+1。循环这步操作。 通过分析粒子群与变邻域搜索算法结构及试验结果,发现粒子群算法和变邻域搜索算法均有各自的优点和不足。 粒子群算法的局部搜索能力较弱,搜索精度较低,所以很容易造成过早收敛的情况,但是变邻域搜索算法具有较好的局部搜索能力且搜索精度也较高。在运算过程中,粒子群算法受历史最优解的影响较大,经过不断的迭代都是在向最优解靠近,缺少了解的多样性,而变邻域搜索算法正好可以弥补这一缺点,通过不断搜索不同邻域,可以跳出局部最优的情况。 粒子群算法收敛速度较快,全局搜索能力较好,主要通过粒子不断向最优解靠近,可以较快地在很大的解空间中找到具有最优解的大致范围。这正好可以弥补变邻域搜索算法收敛速度慢、搜索时间长的缺点,可以给变邻域搜索的开始提供一个高质量的初始解。 为了克服粒子群算法可能产生早熟的现象,考虑到粒子群算法中粒子每次更新都会受到当前解、个体历史最优解和种群历史最优解3个因素的影响,本研究将粒子的更新过程采用变邻域搜索,动态地改变邻域结构来拓展搜索的空间,使算法最终能够跳出局部最优解,搜索到全局最优解。 笔者设计的粒子群混合变邻域搜索算法的基本流程如下: 1)对粒子群状态进行重置。 2)对粒子的适应度值Fit[i]进行计算。 3)个体极值pbest(i)比较,当Fit[i]>pbest(i)时,Fit[i]替换掉pbest(i)。 4)全局极值gbest(i)比较,当Fit [i]>gbest(i)时,Fit [i]替换掉gbest(i)。 5)根据式(14)和式(15)更新粒子的位置Xi和速度Vi。 6)判断是否满足结束条件(误差足够好或者达到最大循环次数),若满足,则算法结束并输出最优结果;若不满足,则返回2)。 7)对粒子进行调用变邻域搜索,主要的搜索策略是:顺序执行各个模块,一旦出现比当前更优秀的中间解,就用中间解代替当前解,继续调用这个模块进行搜索,直到搜索发现更差的中间解出现;否则执行下一模块直到结束。 8)判断是否满足结束条件K 9)输出全局最优值,算法运行结束。 粒子群混合变邻域搜索算法流程图如图3所示。 图3 粒子群变邻域搜索混合算法流程Fig. 3 Flow chart of particle swarm variable neighborhood search hybrid algorithm 图4 实例1的3种算法下料方案对比Fig. 4 Comparison of cutting patterns of three algorithms in the example 1 本研究首先利用粒子群算法进行运算,求出的最优解作为后续变邻域搜索算法的初始解,再用变邻域搜索算法继续进行求解。粒子群算法为后续的变邻域搜索提供了一个较好的初始解,并引导算法寻找更好的解;变邻域搜索是集中邻域搜索在搜索空间附近的较好解。从而提高了算法的全局搜索能力和局部搜索能力,平衡了算法在搜索过程中的普遍性和集中性。 笔者根据某公司产品实际生产情况,选取3种不同需求的下料实例进行分析。 实例1:根据某公司生产的木家具产品实际情况,选取下料板材长度为230 cm、宽度为160 cm的单一规格的规则矩形板材,根据客户需求,需要做3套成品,一共有6种毛坯零件的需求。 毛坯零件的具体尺寸和数量如表1所示。 表1 实例1毛坯零件数据Table 1 Data of panel parts in the example 1 经过计算得到利用粒子群算法的利用率是84.846%,利用变邻域搜索算法的利用率是85.658%,粒子群混合变邻域搜索算法的利用率为92.281%。3种算法具体的下料方案如图4所示,下料都只消耗了1块板材,虽然下料的利用率可以接受,但是从下料的方案中可以看出,前两种下料方案仍有很大的改进空间。粒子群混合变邻域搜索算法相比粒子群算法和变邻域搜索算法的计算都有较大幅度的提升,且通过粒子群混合变邻域搜索算法生成的具体下料方案可以看到,并没有产生面积过大的废料,剩下的余料仍然可以投入后续生产使用。 实例2:选取下料板材为单一规格的规则矩形木材板材,板材的长度为140 cm,宽度为90 cm,现在根据客户要求,需要切割出9种毛坯零件,通过变邻域搜索算法和粒子群算法计算出最优的下料方案。具体的毛坯零件的尺寸数量要求如表2所示。 表2 实例2毛坯零件数据Table 2 Panel parts data in the example 2 实例3:选取下料板材长度为230 cm、宽度为160 cm的单一规格的规则矩形板材,根据客户需求,一共有12种毛坯零件的需求,具体的毛坯零件的尺寸和数量要求如表3所示。 表3 实例3毛坯零件数据Table 3 Panel parts data in the example 3 对于实例1、实例2和实例3同时用粒子群算法、变邻域搜索算法和粒子群混合变邻域搜索算法进行下料计算的结果对比如表4所示。 在表4中,通过粒子群算法和变邻域搜索算法计算结果的对比可以看出,变邻域搜索算法计算出的木材板材的利用率与粒子群算法相近,甚至有时会超过粒子群算法,说明变邻域搜索算法也同样适用于木材板材下料问题的求解。但没有达到预期中的理想效果,仍有需要改进的地方。 通过粒子群算法与粒子群混合变邻域搜索计算结果的对比可以看出,实例1利用率从84.846%提升到92.281%,实例2利用率从83.175%提升到91.244%,实例3从86.238%提升到92.245%,由改进后的粒子群算法计算出的木材板材利用率明显比粒子群算法高出很多。粒子群混合变邻域搜索算法不会受到规格数量的影响,计算出的利用率可以达到90%以上,同时也不会产生面积较大的废料。这也充分证明了本研究提出的将变邻域搜索算法的思想加入粒子群算法中,能够有效解决粒子群算法容易早熟缺陷、局部搜索能力差的问题。 综上所述,本研究3种算法中,最优异且适用的算法为粒子群混合变邻域搜索算法,适合在家具等相关行业木材板材实际生产中进行下料计算,解决了木材板材加工过程中的原材料利用率不高的难题,给家具等相关行业带来了实际的经济效益。 本研究主要根据某公司生产的木家具产品将其转化为单规格的二维矩形下料问题,并将其运用到该企业的生产实际中。在利用离散粒子群进行求解过程中,通过动态改变邻域结构来改善粒子群算法容易陷入早熟的情况。该算法避免了粒子群算法易陷入局部最优解的问题,给变邻域搜索算法提供了质量较高的初始解,加快了算法的收敛速度,使得结果趋于全局最优。为验证算法的可靠性,根据公司生产实例,设计了3组基于利用率的试验分析,通过3种不同的算法对矩形板材进行切割计算,以实例3为例,在选取长度为230 cm、宽度为160 cm的单一规格的规则矩形板材后,改进后的粒子群算法的利用率由86.238%提升为92.245%。实验结果表明,粒子群混合变邻域搜索算法可以有效地节约木材板材资源,提升企业经济效益。
2.3 粒子群混合变邻域搜索算法
3 实例分析


4 结 语

